
In this section, we delve into critical mathematical techniques that are essential for mastering intermediate-level topics. Through a series of detailed steps, we explore methods for solving complex equations and graphing various functions. The focus is on building a deep understanding and practical skills that can be applied to a wide range of problems.
Whether you’re tackling quadratic equations, simplifying expressions, or interpreting graphs, this guide provides the tools and strategies needed to enhance problem-solving abilities. We will walk through common obstacles and offer strategies to overcome them, ensuring a solid grasp of key concepts that are pivotal for further studies.
By the end of this section, you will have a comprehensive understanding of the mathematical principles and be equipped with the skills necessary to approach future challenges with confidence and precision.
Comprehensive Guide to Algebra 2 Module 2
This section provides an in-depth look at key mathematical techniques necessary for advancing through intermediate-level topics. By focusing on foundational concepts and problem-solving strategies, you’ll build a solid base that will aid in tackling more complex challenges. The content is designed to guide you step by step, ensuring that each concept is thoroughly understood and can be applied confidently.
Understanding Key Concepts

In this section, you will encounter several critical concepts that form the core of the subject. These include techniques for solving equations, manipulating expressions, and interpreting mathematical relationships. Here are the key areas you will explore:
- Solving and graphing quadratic equations
- Factoring and simplifying expressions
- Understanding polynomial functions
- Working with rational expressions
- Applying algebraic identities
Problem-Solving Strategies
To ensure success in these areas, it is essential to adopt effective problem-solving strategies. The following approaches will help you work through challenges efficiently:
- Break down complex problems into smaller, manageable parts
- Use visual aids like graphs and tables to clarify relationships
- Check your solutions at each step to avoid errors
- Practice with a variety of examples to reinforce your understanding
- Review key formulas and concepts regularly
By mastering these strategies, you will enhance both your theoretical knowledge and practical skills, ensuring that you can tackle a wide range of mathematical problems with ease.
Understanding Key Concepts in Algebra 2
In this section, we focus on the essential principles that lay the foundation for more advanced mathematical study. Understanding these concepts is crucial for solving various types of equations and functions. By grasping these key ideas, you will be able to approach problems with confidence and precision, ensuring a deeper comprehension of the subject.
Important Topics to Master
To build a strong mathematical base, there are several core topics you must familiarize yourself with. These include various methods of solving and simplifying equations, as well as understanding the properties of different functions. Below are the primary areas covered:
- Quadratic equations and their properties
- Factoring polynomials and simplifying expressions
- Graphing and analyzing different types of functions
- Rational expressions and their simplifications
- Solving systems of equations using various techniques
Key Strategies for Success
Grasping these concepts requires more than just memorizing formulas. It is important to develop strategies that allow you to apply these principles effectively in problem-solving. Here are a few approaches to help you succeed:
- Identify the type of problem and the appropriate method to solve it
- Use diagrams and graphs to visualize relationships
- Practice regularly to reinforce your understanding
- Work through example problems step-by-step
- Review foundational formulas and their applications
By focusing on these key concepts and strategies, you will be well-equipped to approach more complex mathematical challenges with clarity and ease.
Mastering Problem-Solving Techniques
Effective problem-solving is at the heart of mastering complex mathematical challenges. Developing a systematic approach to tackle various types of problems allows you to work through them with confidence and efficiency. This section will help you hone the skills necessary to break down and solve problems step by step, ensuring a comprehensive understanding of key concepts.
Approaches for Tackling Complex Problems

To effectively solve problems, it’s essential to approach them methodically. By using the right strategies, you can simplify even the most challenging tasks. Below are several techniques that will guide you through difficult problems:
- Identify the problem type and choose the best solution strategy
- Write out all given information clearly and organize it systematically
- Look for patterns or relationships between variables
- Break the problem into smaller, more manageable steps
- Double-check your work to ensure accuracy at every stage
Tools and Resources for Efficient Problem Solving
In addition to the right mindset and strategies, certain tools can enhance your ability to solve problems. These resources help simplify calculations and provide visual clarity:
- Use a graphing calculator for complex functions and equations
- Draw diagrams or charts to visualize relationships between variables
- Refer to formulas and identities to save time and ensure accuracy
- Consult practice problems to familiarize yourself with different types of questions
By combining these techniques with regular practice, you will be able to solve even the most challenging problems with ease and precision.
Step-by-Step Solutions for Algebra 2
Breaking down complex problems into manageable steps is essential for mastering mathematical concepts. In this section, we will walk through detailed solutions to various types of problems, helping you understand each phase of the process. The goal is to equip you with the skills needed to solve problems efficiently, using a structured approach that can be applied to similar tasks.
Step 1: Analyze the Problem
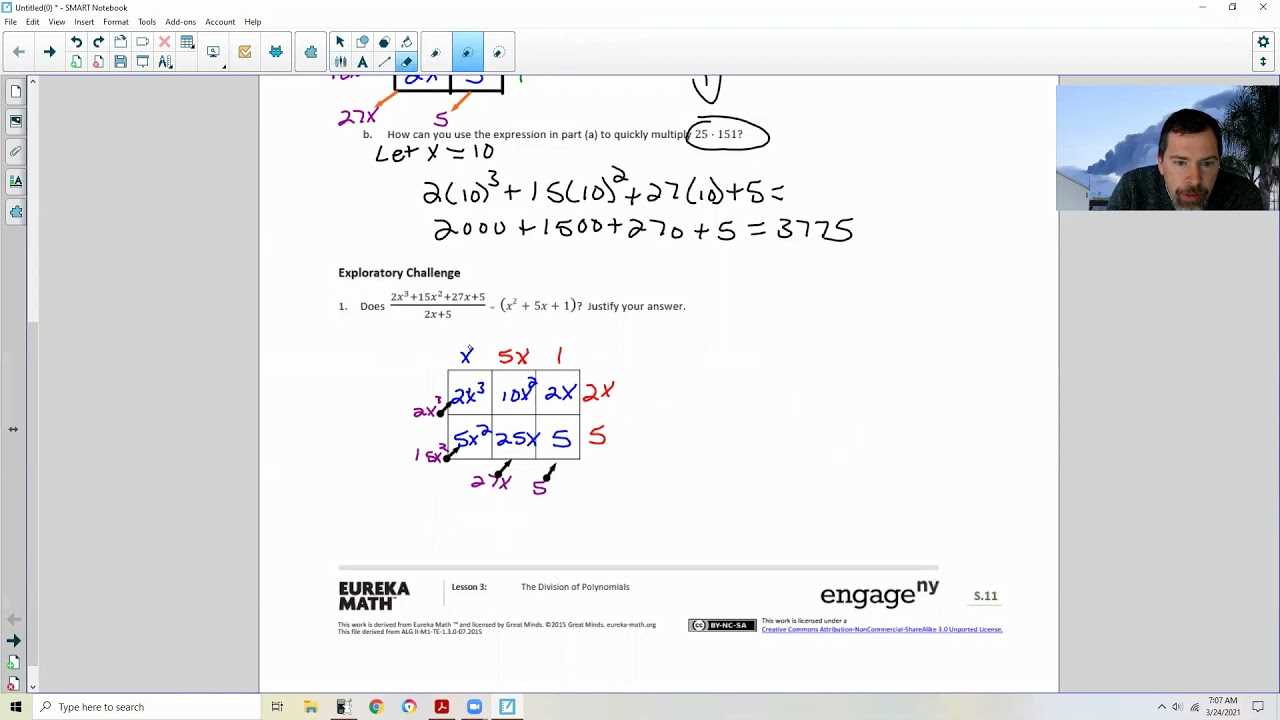
The first step in solving any mathematical problem is to carefully read and analyze the given information. This ensures you understand what is being asked and what tools or methods you will need. Here are some important things to consider:
- Identify the type of equation or expression
- Write down all known values and variables
- Recognize patterns or similarities with previously solved problems
Step 2: Solve Using Appropriate Methods

Once the problem is clearly understood, choose the correct method to solve it. Below are common strategies for various problem types:
- For equations: isolate the variable using addition, subtraction, multiplication, or division
- For graphing: plot points on a coordinate plane and draw the corresponding curve or line
- For factoring: use methods like factoring by grouping or using the quadratic formula
Step 3: Verify Your Solution
After obtaining a solution, it’s important to verify its accuracy. Double-checking your work helps ensure no errors have been made. Here’s how you can check:
- Substitute your solution back into the original equation
- Ensure all steps were followed correctly and logically
- Review your final result to confirm it makes sense in the context of the problem
By following this step-by-step approach, you will improve your problem-solving skills and be better prepared for more complex challenges.
Common Challenges in Module 2
As students progress through more advanced topics, they often encounter challenges that can seem overwhelming at first. In this section, we will discuss some of the most common difficulties faced when dealing with intermediate-level equations, functions, and problem-solving techniques. Understanding these challenges will help you prepare and overcome obstacles as you work through the material.
Difficulty with Quadratic Equations
One of the most common challenges is solving quadratic equations. While the process may seem straightforward, it often requires careful attention to detail. Students may struggle with identifying the right method, whether it’s factoring, completing the square, or using the quadratic formula. To overcome this challenge, it is important to:
- Identify the form of the equation (standard, vertex, factored)
- Practice different methods to build fluency
- Ensure all steps are followed correctly, especially when simplifying
Working with Rational Expressions
Another challenge many students face is simplifying and solving rational expressions. These problems require a solid understanding of how to manipulate fractions with variables and how to factor both numerators and denominators. Key difficulties include:
- Identifying and canceling common factors
- Dealing with complex denominators
- Solving equations involving rational expressions while keeping track of restrictions
By practicing these areas and focusing on the underlying principles, you will be able to navigate these common challenges with greater ease.
How to Tackle Quadratic Equations
Quadratic equations are a fundamental topic that can often present challenges, but with the right approach, they can be tackled efficiently. Understanding the different methods for solving these equations is essential for mastering the concept. Whether you are factoring, completing the square, or applying the quadratic formula, each technique offers a clear path to finding the solution.
Different Methods to Solve Quadratic Equations

There are several methods available for solving quadratic equations, and selecting the right one depends on the form of the equation. Here are the most common techniques:
| Method | When to Use | Steps |
|---|---|---|
| Factoring | When the equation can be factored easily | 1. Rewrite the equation in standard form 2. Factor the quadratic expression 3. Set each factor equal to zero and solve |
| Completing the Square | When the equation is not easily factorable but can be rewritten as a perfect square | 1. Move the constant to the other side 2. Add the square of half the coefficient of x to both sides 3. Take the square root of both sides and solve |
| Quadratic Formula | When factoring is difficult or impossible | 1. Use the formula: x = (-b ± √(b² – 4ac)) / 2a 2. Substitute the values of a, b, and c 3. Simplify to find the solutions |
Choosing the Best Method
Each method has its advantages, and the choice of which one to use depends largely on the equation you are working with. For simple equations that factor easily, factoring is the quickest approach. For equations that are not factorable, completing the square or using the quadratic formula may be more efficient. By practicing each method, you’ll become more comfortable with identifying the best strategy for solving quadratic equations.
Graphing Functions in Algebra 2
Graphing is a powerful way to visualize mathematical relationships between variables. By plotting a function on a coordinate plane, you can gain insights into its behavior, such as its intercepts, slopes, and the overall shape of the graph. Understanding how to graph different types of functions is a crucial skill that helps you analyze and interpret mathematical problems more effectively.
There are various types of functions you will encounter, each with unique graphing methods. Linear, quadratic, and exponential functions, for example, each have distinct characteristics when graphed. Learning to identify these features will help you accurately represent them on a graph and understand how changes in the equation affect the graph’s shape and position.
To graph a function, start by determining its key points, such as intercepts and turning points. From there, you can plot additional points, connect them, and analyze the function’s behavior over the entire domain. With practice, graphing functions becomes a valuable tool for solving problems and visualizing complex relationships.
Exploring Polynomial Expressions
Polynomial expressions are fundamental in understanding many areas of mathematics. These expressions, which involve sums of terms with variables raised to different powers, can model a wide range of real-world phenomena. By studying how polynomials behave and how to manipulate them, you can solve more complex equations and understand the relationships between different variables.
Components of a Polynomial Expression
Each polynomial consists of terms that include a coefficient and a variable raised to an exponent. The general form of a polynomial expression is the sum of these terms. Understanding the components is key to simplifying and solving polynomial equations:
- Coefficients: The numerical factors in each term.
- Exponents: The powers to which the variable is raised.
- Degree: The highest exponent in the polynomial.
Operations on Polynomial Expressions
Working with polynomial expressions often involves various operations, such as addition, subtraction, multiplication, and division. Each operation follows certain rules that simplify the process:
- Adding and subtracting polynomials: Combine like terms with the same degree.
- Multiplying polynomials: Distribute each term in one polynomial to every term in the other polynomial.
- Dividing polynomials: Use long division or synthetic division for more complex expressions.
Mastering these operations allows you to simplify and manipulate polynomials, making them easier to analyze and solve in various mathematical contexts.
Important Theorems to Know
In mathematics, theorems provide essential principles that form the foundation for solving problems and proving various concepts. Understanding key theorems is crucial for advancing in mathematical studies and for tackling more complex equations and expressions. These theorems offer powerful tools that can simplify calculations, offer new insights, and help solve real-world problems.
Fundamental Theorems
There are several important theorems that every student should be familiar with. These include:
- Fundamental Theorem of Algebra: Every non-constant polynomial equation has at least one complex root.
- Factor Theorem: If a polynomial f(x) has a factor (x – a), then f(a) = 0.
- Remainder Theorem: When dividing a polynomial f(x) by (x – a), the remainder is f(a).
Key Applications of Theorems
These theorems can be applied in various ways, particularly in solving polynomial equations, factoring expressions, and finding roots. They are invaluable for simplifying complex problems and form the basis for more advanced techniques used in higher mathematics.
Utilizing the Discriminant Formula
The discriminant is a key concept in solving quadratic equations, providing valuable insight into the nature of their solutions. By analyzing the discriminant, you can determine whether an equation has real or complex roots, and if real roots exist, how many there are. This formula helps to quickly assess the equation’s behavior without needing to fully solve it first.
Understanding the Discriminant
The discriminant is the part of the quadratic formula under the square root, represented as b² – 4ac. It plays a crucial role in identifying the number and type of solutions:
- Positive Discriminant: Two distinct real solutions.
- Zero Discriminant: One real solution (a repeated root).
- Negative Discriminant: Two complex solutions (no real roots).
How to Use the Discriminant
To use the discriminant effectively, first identify the coefficients of the quadratic equation in the form ax² + bx + c = 0. Then, calculate the value of b² – 4ac to determine the nature of the solutions. This can save time and provide a clear understanding of the equation’s behavior before attempting to solve it completely.
Strategies for Factoring Expressions
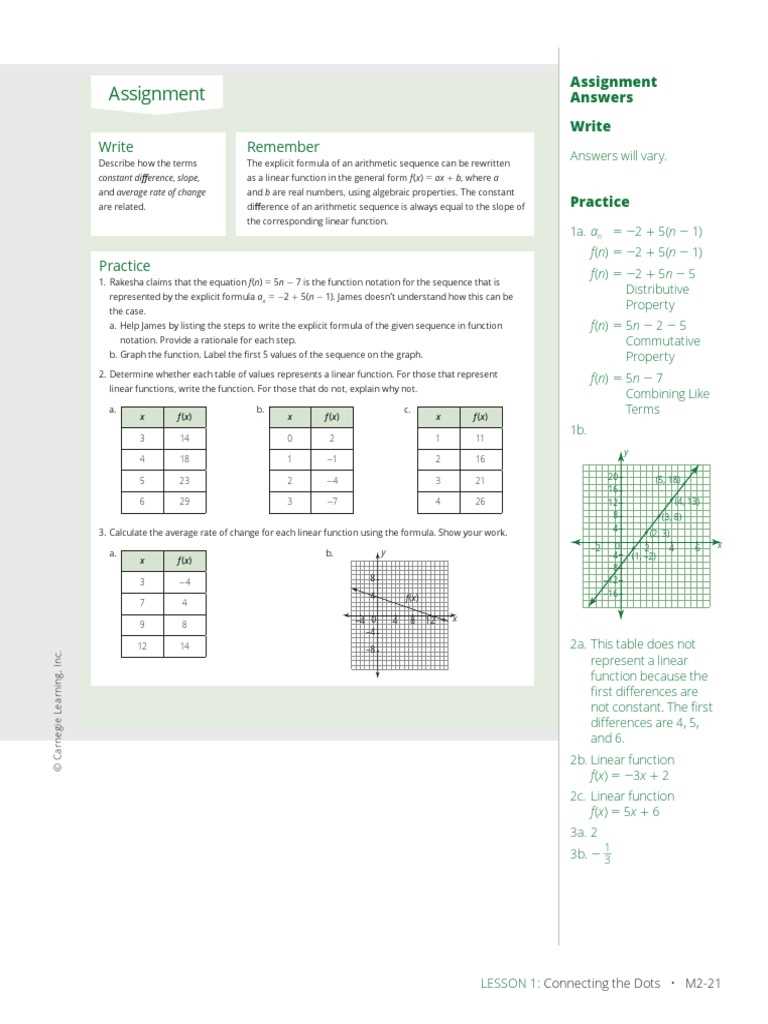
Factoring expressions is a crucial skill in simplifying mathematical problems and solving equations. It involves breaking down complex expressions into simpler components, making them easier to work with. Whether you’re dealing with polynomials, quadratic equations, or higher-order expressions, mastering factoring techniques is essential for solving a variety of mathematical challenges.
Common Factoring Methods
There are several strategies for factoring expressions, each suitable for different types of problems. Some of the most frequently used methods include:
- Common Factor Extraction: Identifying and factoring out the greatest common factor (GCF) from all terms in the expression.
- Factoring by Grouping: Splitting the expression into groups that can be factored individually, then combining them.
- Difference of Squares: Factoring expressions of the form a² – b² into (a + b)(a – b).
- Trinomial Factoring: Factoring quadratic trinomials into two binomials of the form (x + p)(x + q).
Step-by-Step Example
Here’s an example of how to factor a simple trinomial:
| Step | Action |
|---|---|
| 1 | Identify the quadratic expression: x² + 5x + 6. |
| 2 | Find two numbers that multiply to 6 and add up to 5 (in this case, 2 and 3). |
| 3 | Write the factored form: (x + 2)(x + 3). |
By applying these strategies and practicing regularly, you can become proficient at factoring different types of expressions efficiently and accurately.
Solving Rational Functions Effectively
Rational functions are expressions that involve ratios of polynomials. Solving problems that involve these functions requires a strong understanding of their behavior, including their domain, asymptotes, and intercepts. By breaking down the components of rational expressions, you can simplify them and find solutions more effectively. The key to solving such equations lies in clear steps that allow you to manage complex expressions with ease.
Steps for Solving Rational Functions
To solve rational functions, follow these essential steps:
- Simplify the expression: Factor the numerator and denominator to identify any common factors that can be canceled out.
- Find the domain: Determine any values that make the denominator equal to zero, as these values are excluded from the domain.
- Set the expression equal to zero: To solve for the variable, set the rational expression equal to zero and solve the resulting equation.
- Check for extraneous solutions: Ensure that the solutions do not result in undefined values, such as making the denominator zero.
Example: Solving a Rational Equation
Consider the rational equation (x + 2) / (x – 3) = 4. To solve:
- Step 1: Multiply both sides of the equation by (x – 3) to eliminate the denominator: (x + 2) = 4(x – 3).
- Step 2: Simplify and solve the resulting equation: x + 2 = 4x – 12.
- Step 3: Move terms to isolate the variable: 14 = 3x, so x = 14/3.
- Step 4: Verify that x = 14/3 does not make the denominator zero in the original equation.
By following these steps, you can solve rational functions with confidence, ensuring both accuracy and efficiency.
Using Algebraic Identities in Module 2
Algebraic identities play a crucial role in simplifying and solving various types of equations. These identities are foundational tools that allow you to manipulate and transform expressions more efficiently. By recognizing patterns and applying these formulas, you can reduce complex problems to simpler forms, making it easier to solve them accurately. In this section, we will explore the key identities used in the context of the current topic and how to apply them effectively.
Key Algebraic Identities
Below are some of the most common algebraic identities that can help simplify and solve equations in this context:
| Identity | Formula | Example |
|---|---|---|
| Difference of Squares | a² – b² = (a – b)(a + b) | x² – 9 = (x – 3)(x + 3) |
| Perfect Square Trinomial | a² + 2ab + b² = (a + b)² | x² + 6x + 9 = (x + 3)² |
| Sum of Cubes | a³ + b³ = (a + b)(a² – ab + b²) | x³ + 8 = (x + 2)(x² – 2x + 4) |
| Difference of Cubes | a³ – b³ = (a – b)(a² + ab + b²) | x³ – 27 = (x – 3)(x² + 3x + 9) |
These identities are essential for simplifying expressions, solving equations, and factoring polynomials. By mastering their application, you can approach more complex problems with greater ease and confidence.
Checking Your Work for Accuracy
Ensuring the correctness of your solutions is a vital step in the problem-solving process. It’s easy to make small mistakes, and verifying your work helps to catch errors that might have been overlooked. Whether you are solving equations or simplifying expressions, confirming the steps and final answer can save you time and prevent confusion later on. In this section, we’ll explore several methods and strategies to effectively check your work.
Techniques for Verification

There are several methods you can use to verify your results:
- Substitute Back Into the Original Equation: One of the simplest methods is to plug your solution back into the original equation to check if both sides are equal. This ensures that the solution satisfies the equation.
- Use a Different Approach: If possible, solve the problem using a different method or approach to see if you reach the same result. For example, you can factor an expression or use a different formula to double-check the answer.
- Estimate and Approximate: Before solving, try estimating the answer based on the given numbers. If your result is far off from the estimate, it’s a signal that you should recheck your steps.
Common Mistakes to Watch For
When checking your work, be mindful of common errors that tend to occur:
- Sign Errors: Double-check the signs (positive or negative) in your calculations, as small sign mistakes can lead to big errors in the final answer.
- Misapplication of Formulas: Ensure that you’re using the correct formulas and applying them in the proper order. Incorrect substitution or overlooking a variable can skew your results.
- Arithmetic Mistakes: Always review your basic arithmetic, especially in multi-step problems where errors in adding, subtracting, or multiplying can easily be overlooked.
By adopting a methodical approach and reviewing your steps carefully, you can ensure that your solutions are accurate and reliable.
Tips for Preparing for Tests

Effective preparation is key to performing well in any test, especially when dealing with complex topics. The goal is to understand the underlying concepts thoroughly and be able to apply them efficiently during the exam. By using a strategic approach, you can ensure that you are ready and confident when it’s time to sit down for your test.
Study Strategies
Here are some helpful study tips to get you prepared:
- Practice Regularly: Consistent practice is essential. Work on a variety of problems to strengthen your understanding of different concepts. Don’t just focus on easy problems–tackle the more challenging ones as well.
- Review Past Tests: Go over previous tests or assignments to identify areas where you struggled. This will give you insight into common mistakes and help you target your weaknesses.
- Create a Study Schedule: Plan your study sessions in advance, allowing time for each topic. Break down your study material into manageable chunks and avoid cramming the night before.
- Use Study Aids: Make use of textbooks, online resources, or video tutorials to clarify any doubts. Study guides and practice tests are also useful tools to solidify your understanding.
Test-Taking Tips
When it’s time for the actual exam, these tips will help you maximize your performance:
- Read the Instructions Carefully: Before jumping into the questions, take a moment to read the instructions thoroughly to avoid any misunderstandings or mistakes.
- Manage Your Time: Keep track of time and ensure that you allocate enough time to each question. Don’t get stuck on difficult problems for too long–move on and come back to them later if needed.
- Show Your Work: Write out your steps clearly and logically. Even if you don’t arrive at the correct answer, showing your thought process may help you earn partial credit.
- Stay Calm: Test anxiety can impact your performance, so try to remain calm. Take deep breaths and approach each question with a clear mind.
By implementing these study and test-taking strategies, you’ll be in a much better position to succeed and achieve the results you’re aiming for.
Reviewing Key Solutions
Reviewing the solutions to complex problems is an essential part of mastering any topic. By thoroughly going through the correct steps and comparing them to your own work, you can identify areas of strength and opportunities for improvement. This process helps solidify understanding and boosts confidence in solving similar problems in the future.
Steps for Effective Review
To make the most of reviewing solutions, follow these steps:
- Understand Each Step: Go over each step of the solution carefully. Don’t just look at the final answer; instead, focus on the method used to arrive at it. Understanding the reasoning behind each step is crucial for long-term retention.
- Compare with Your Work: Check your solutions against the provided answer key. Pay attention to any differences and try to understand why your approach may have been different. This can help you correct misconceptions.
- Identify Mistakes: If your solution differs from the correct one, identify where things went wrong. Was it a calculation error, a misunderstanding of the problem, or an incorrect assumption? Correcting these mistakes will help you avoid them in future problems.
- Use the Key as a Learning Tool: Don’t just use the answer key to check your answers; use it to learn new methods and techniques. If the solution uses a different strategy than you would have, try understanding and applying that method to other problems.
Common Pitfalls to Watch For
While reviewing the solution key, be mindful of the following common pitfalls:
- Overlooking Small Mistakes: Sometimes, small errors can lead to incorrect answers. Ensure that you haven’t skipped any details, even if they seem minor.
- Assuming the Solution is Always the Same: Every problem may have multiple approaches. Don’t get stuck in thinking that the only way to solve a problem is the way the answer key shows. Consider alternate methods that might work better for you.
- Not Reviewing the Full Problem: Don’t just look at the final answer. It’s important to review the entire problem and solution process to understand how each part connects.
By systematically reviewing the answer key, you can greatly improve your problem-solving skills and avoid making the same errors in future tasks. This thorough review process will help you gain a deeper understanding and achieve better results in the future.