
Preparing for an advanced math assessment can be challenging, but with the right approach, you can improve your chances of achieving a high score. This guide is designed to help you navigate the complexities of the test, offering insight into the key areas that are frequently evaluated. Understanding how to tackle the questions and apply your knowledge is essential for success.
Through focused practice and reviewing detailed solutions, you will gain a deeper understanding of the concepts and problem-solving techniques that are crucial for this assessment. Whether you’re working through sample problems or analyzing your mistakes, this process will help build confidence and sharpen your skills.
By familiarizing yourself with the structure of the test and the most common question types, you will be better equipped to manage your time effectively and approach each section with clarity. Success in this challenge lies not only in what you know but also in how you apply that knowledge under time pressure.
AP Calculus BC Practice Test Solutions
Mastering advanced mathematics requires not just understanding the theory, but also applying it effectively in problem-solving scenarios. In this section, we will explore various types of questions that often appear in the assessment, along with the detailed steps to solve them. By reviewing these examples, you can gain valuable insights into the techniques needed to answer complex problems with precision and confidence.
Approaching Complex Problem Types
For many students, the most challenging aspect is tackling intricate questions that require a deeper understanding of mathematical concepts. These problems often test your ability to integrate multiple topics and apply various methods simultaneously. Understanding the structure of these problems and recognizing key patterns can significantly improve your ability to solve them quickly and accurately. Whether it’s analyzing functions, interpreting graphs, or applying limits, being familiar with these steps is crucial for success.
Step-by-Step Solution Breakdown

Breaking down each question into manageable steps is an effective strategy for approaching even the most difficult problems. First, identify the known variables and what the question is asking. Then, use the appropriate formulas or techniques to solve the problem. Working through solutions methodically allows you to minimize mistakes and ensures you stay focused throughout the assessment. By understanding the reasoning behind each solution, you can apply these strategies to similar questions in the future with confidence.
Understanding the Test Format
Familiarizing yourself with the structure of a major assessment is a key step in effective preparation. Understanding how questions are presented and what types of problems you will encounter helps reduce anxiety and ensures you’re ready to approach each section with clarity. Knowing what to expect allows you to allocate your time wisely and apply the most suitable strategies for different types of questions.
The test typically consists of multiple sections designed to assess a wide range of skills. These may include both multiple-choice questions, where you select the correct answer from a set of options, and free-response questions, where you are required to show your work and provide detailed explanations. Each section has its own time limits, so effective time management becomes crucial in maximizing your performance.
Understanding the weighting of each section is also important. The multiple-choice section generally contributes to a larger portion of your score, but the free-response section tests your ability to explain and justify your reasoning. Both sections require careful preparation and practice to ensure that you can answer each question with confidence and precision.
Key Topics Covered in the Test
In order to succeed in any comprehensive assessment, it’s essential to understand the core concepts that will be tested. The areas of focus are typically designed to evaluate a student’s ability to apply various mathematical principles in real-world scenarios. Familiarity with the key topics ensures that you can approach each section with confidence and employ the correct techniques to solve complex problems.
The topics often covered include concepts like differentiation and integration, which are fundamental in understanding the behavior of functions. Other areas of focus may involve limits, sequences, and series, which require a deep understanding of their applications and how they relate to one another. Additionally, expect to encounter questions about vector functions, polar coordinates, and differential equations, all of which test your ability to work with advanced mathematical models.
Effective Study Strategies for Success
Achieving success in a rigorous assessment requires more than just reviewing material; it involves adopting a focused and strategic approach to learning. Effective study habits can make all the difference in your ability to grasp complex concepts, retain key information, and apply it under pressure. Developing a clear plan and sticking to it will set you up for optimal performance.
One useful approach is to break down your study sessions into manageable chunks, allowing you to focus on specific topics without feeling overwhelmed. Incorporating active recall, where you test your knowledge regularly, helps reinforce concepts and improves retention. Additionally, using practice problems to simulate test conditions can build your confidence and ensure you’re prepared for a wide range of questions.
| Study Strategy | Description |
|---|---|
| Active Recall | Test your knowledge by retrieving information from memory, rather than just reading or reviewing notes. |
| Spaced Repetition | Review material at increasing intervals to strengthen memory retention over time. |
| Practice Problems | Work through various problems regularly to simulate the test environment and familiarize yourself with different question types. |
| Concept Mapping | Create visual diagrams that show the relationships between key concepts, making them easier to recall. |
| Group Study | Collaborate with peers to discuss difficult topics, exchange knowledge, and solve problems together. |
How to Approach Multiple Choice Questions
When facing a set of multiple-choice questions, it’s essential to use a strategic method to maximize your chances of selecting the correct answer. These questions test both your knowledge and your ability to process information quickly under pressure. A focused approach can help you eliminate incorrect options, manage your time efficiently, and increase your accuracy during the assessment.
Read Carefully and Eliminate Incorrect Options
Start by reading each question thoroughly, making sure to understand exactly what it’s asking before looking at the options. Often, multiple choices will include distractors that are designed to seem plausible. If you’re unsure of the correct answer, try to eliminate the obviously incorrect options first. This increases your odds of selecting the correct one from the remaining choices.
Time Management and Guessing Strategy

Time management is crucial, so don’t spend too long on any one question. If you’re stuck, make an educated guess and move on, especially when you’re running low on time. It’s better to answer every question, even with a guess, than to leave any blank, as there is no penalty for incorrect answers. Review any questions you skipped if time allows, but prioritize completing all items first.
Solving Free Response Problems Efficiently
Free-response questions can often feel more challenging than multiple-choice questions, as they require not only the correct answer but also a clear and organized explanation of your reasoning. Developing an efficient approach to solving these types of problems can significantly improve both the speed and quality of your responses. The key is to break down each problem into manageable steps and demonstrate your thought process clearly.
When approaching these questions, it’s important to begin by reading the prompt carefully, highlighting key information, and determining what is being asked. Once you have a clear understanding, outline your solution before jumping into calculations. This helps to avoid mistakes and ensures that your solution is logical and easy to follow. Keep in mind that showing your work is just as important as arriving at the correct answer.
| Step | Action |
|---|---|
| Read the Prompt | Identify the key information and understand the problem’s requirements. |
| Plan Your Approach | Outline the steps needed to solve the problem before starting calculations. |
| Show All Work | Provide clear, logical steps to demonstrate how you arrived at the solution. |
| Check for Errors | Review your work for any potential mistakes, especially in calculations and reasoning. |
| Be Concise | Present your solution in a clear and concise manner to avoid unnecessary complexity. |
Common Mistakes to Avoid on the Exam
During high-stakes assessments, it’s easy to fall into the trap of common errors that can undermine your performance. These mistakes can stem from misreading the questions, overlooking key details, or rushing through problems without proper consideration. Avoiding these pitfalls will help you maintain focus and improve the overall quality of your responses.
Overlooking Key Details
Sometimes, the most obvious answers aren’t the correct ones, and important details can be easily missed if you’re not careful. It’s essential to pay close attention to every part of the question, especially the instructions or constraints provided. Misinterpreting or ignoring these can lead to errors that could have been easily avoided.
- Failing to address all parts of the question
- Overlooking units or rounding instructions
- Misreading negative signs or coefficients
Rushing Through Problems

While time management is important, rushing through questions can lead to avoidable mistakes. It’s essential to pace yourself and ensure that each solution is carefully worked through. This is especially true for complex problems that require step-by-step analysis. Taking a moment to double-check your work can save you from costly errors.
- Skipping over steps in calculations
- Failing to check answers for consistency
- Not reviewing work before submitting
Time Management Tips for Test Day
Efficiently managing your time during a high-stakes assessment is crucial for success. Without a clear strategy, it’s easy to waste precious moments on difficult questions or rush through others. Planning how to allocate your time for each section ensures you can maximize your performance and complete the test with confidence.
Prioritize Your Tasks
Start by assessing the layout of the test and identifying which sections or questions you can handle more quickly. Allocate extra time to more challenging problems, but don’t spend too long on any single question. Knowing when to move on and come back later can help you manage your time effectively.
- Read through all sections before starting
- Set time limits for each section
- Save difficult questions for the end
Maintain a Steady Pace
Throughout the test, try to keep a consistent pace. Don’t rush but avoid lingering too long on any one problem. If you find yourself stuck, move forward and revisit the question later. This approach allows you to maintain momentum and ensures you won’t run out of time before finishing.
- Monitor your progress at regular intervals
- Use a timer or watch to track time
- Stay calm and don’t let pressure affect your pace
Interpreting Graphs and Diagrams Correctly
Graphs and diagrams are valuable tools that help convey complex information in a visual format. However, they can also present challenges if not interpreted properly. Understanding the key elements of a graph or diagram, such as axes, labels, and trends, is essential to accurately solve problems and extract meaningful conclusions from them.
Key Elements to Focus On

Before diving into problem-solving, take a moment to examine the various components of the graph or diagram. This includes checking the scale of axes, identifying important labels, and noting any key points, such as maxima, minima, or intercepts. A thorough review of these details will help you avoid missing critical information.
- Examine the axes and their labels
- Identify any key points or trends
- Check for units or scale markers
Common Pitfalls to Avoid
One common mistake is misreading the graph’s scale or assuming that trends continue indefinitely without verifying. Another issue arises when failing to consider all relevant parts of the graph, like sections that may seem irrelevant at first but are critical to solving the problem. Always question whether you have reviewed all information carefully before proceeding.
- Don’t ignore the scale or intervals between points
- Don’t assume trends are linear without verification
- Ensure you analyze the entire graph or diagram
Using Calculators Effectively During the Test

While calculators can be a helpful tool during assessments, knowing when and how to use them is crucial for maximizing their effectiveness. A calculator can speed up tedious calculations, but relying too heavily on it may lead to missed opportunities for deeper understanding or errors in interpreting the results. Understanding the best strategies for using a calculator can help optimize performance.
When to Use the Calculator

The calculator should be used to simplify lengthy calculations, especially when dealing with large numbers or complicated expressions. However, before reaching for the calculator, make sure you understand the problem and have a strategy for how to approach it. For simpler calculations, it is often more beneficial to solve them manually, as this reinforces your understanding of the concepts.
- Use for long calculations or repetitive steps
- Use to verify results when unsure of manual calculations
- Avoid using for simple arithmetic that can be done mentally
Common Mistakes to Avoid
One common mistake is entering incorrect information into the calculator, leading to inaccurate results. Always double-check your inputs before hitting the ‘equals’ button. Another mistake is over-relying on the calculator for problems that require conceptual understanding. Ensure that you understand the logic behind each step before resorting to technology.
- Double-check inputs and ensure the correct settings
- Avoid using the calculator for tasks that require understanding of underlying principles
- Don’t neglect to work through problems without the calculator for practice
Commonly Tested Theorems and Formulas
In any high-level mathematical assessment, there are certain key principles and equations that are frequently tested. These concepts are fundamental for solving complex problems, and having them memorized can significantly improve performance. Understanding and applying these theorems and formulas is essential for tackling a wide variety of questions effectively.
Some of the most important theorems and formulas often covered include integral and derivative properties, as well as theorems related to sequences and series. These principles provide the foundation for solving many advanced problems, so it’s crucial to familiarize yourself with their applications and implications.
Key Theorems
Several theorems play a critical role in helping solve complex problems efficiently. Here are a few of the most essential:
- The Fundamental Theorem of Calculus – connects derivatives and integrals, forming the backbone of many problem-solving techniques.
- Mean Value Theorem – relates average rates of change to instantaneous rates of change, often used to understand behavior within specific intervals.
- Intermediate Value Theorem – ensures that continuous functions take on all values between two points, useful for finding solutions to equations within a certain range.
Essential Formulas
In addition to theorems, having a strong grasp of key formulas is equally important. Some of the most frequently used include:
- Power Rule – a fundamental formula for differentiation and integration of polynomial expressions.
- Integration by Parts – a method for integrating products of functions, essential for handling more complex integrals.
- Taylor Series – an approximation technique that expresses functions as an infinite sum of terms based on derivatives at a single point.
Tips for Preparing for AP Calculus BC
Preparing for a challenging math assessment requires focused effort, strategic planning, and a deep understanding of core concepts. Success in this type of evaluation depends on mastering key principles, practicing problem-solving techniques, and ensuring you can apply them under pressure. Below are some essential strategies to help you get ready effectively.
Study Techniques
Establishing a solid study routine is vital for mastering the material. Here are some proven approaches to help you prepare:
- Review Past Topics Regularly: Revisit earlier material frequently to reinforce your understanding and ensure you don’t forget foundational concepts.
- Practice Problem-Solving: Consistent practice with a variety of questions helps familiarize you with the format and types of problems that may arise.
- Seek Help When Needed: Don’t hesitate to ask teachers, tutors, or peers for clarification on complex topics.
Time Management

Effective time management during preparation is crucial to avoid last-minute cramming and ensure comprehensive understanding:
- Set Clear Goals: Break down the material into manageable sections and set specific goals for each study session.
- Use Timed Practice Sessions: Simulate timed practice runs to build stamina and improve your ability to manage time under test conditions.
- Take Breaks: Avoid burnout by taking regular breaks during study sessions to refresh your mind and maintain focus.
Familiarize Yourself with Resources
Using available resources can give you an edge. Consider the following:
- Textbooks and Study Guides: Comprehensive materials provide detailed explanations and offer practice problems to reinforce your learning.
- Online Tools: Use online platforms that offer interactive lessons, practice questions, and video tutorials to supplement your study routine.
- Form Study Groups: Collaborating with peers can provide new insights and help clarify challenging concepts.
Reviewing Practice Questions and Solutions

Reviewing questions and their corresponding solutions is one of the most effective ways to solidify your understanding of key concepts and improve problem-solving skills. By analyzing both the process and the correct answers, you can gain valuable insights into your strengths and areas for improvement. This approach helps reinforce learning and builds confidence when facing similar problems in a high-pressure setting.
Understanding the Problem-Solving Process
Simply reviewing the correct answer is not enough. To truly benefit from working through problems, focus on understanding the thought process behind each step:
- Break Down Each Step: Carefully examine each step in the solution to understand how and why it was performed. This helps internalize the methods used.
- Identify Patterns: Look for common patterns in problems and solutions, as this can speed up your problem-solving ability in future tasks.
- Practice Different Approaches: For more complex problems, try solving them in various ways to deepen your comprehension and flexibility with the material.
Analyzing Mistakes and Gaining Insights
When reviewing your incorrect responses, it is crucial to understand where things went wrong and how to avoid similar mistakes in the future:
- Highlight Errors: Focus on identifying why a particular step was incorrect, and pinpoint the reasoning or calculation error that led to the wrong answer.
- Learn from Mistakes: Mistakes provide valuable lessons. After understanding the error, rework similar problems to reinforce the correct approach.
- Ask for Feedback: If you’re unsure why an answer is wrong, seek clarification from a teacher or peer to ensure a clear understanding.
How to Analyze Past Exam Questions
Analyzing previous questions can be a powerful tool for understanding the structure and content of assessments. By reviewing past problems, you can identify recurring themes, question formats, and specific skills that are often tested. This method not only helps improve your familiarity with the material but also enhances your ability to approach new challenges effectively.
Identify Key Concepts and Skills
Start by focusing on the concepts and techniques that are consistently featured across multiple questions:
- Highlight Core Topics: Pay attention to topics that appear frequently in past questions, as they are likely to be fundamental to the assessment.
- Understand Problem Types: Categorize questions based on the type of problem they represent (e.g., theoretical, computational, application-based), which helps in targeting specific skills.
- Track Progression of Difficulty: Observe how the difficulty level progresses in past questions. This can give you an idea of how complex problems might become during an actual assessment.
Refine Your Approach Through Review

Once you have identified the key concepts, it’s time to refine your approach to solving these problems:
- Review Solutions Thoroughly: Don’t just look at the answers, but understand the reasoning behind each step. This helps you grasp the methodology used in solving the problems.
- Analyze Mistakes: Go over your incorrect responses to pinpoint where you went wrong. Learning from mistakes helps you avoid repeating them in the future.
- Practice Timed Problem Solving: Simulate real-time conditions by solving past questions within a set time frame. This will help you manage your time effectively during the actual assessment.
Practice Test Resources for AP Calculus BC
To effectively prepare for the assessment, utilizing a variety of resources for mock questions and solutions is crucial. These materials can provide insight into the types of problems that are likely to appear and help you gauge your preparedness. Whether it’s through online platforms, textbooks, or official materials, having access to quality resources allows you to strengthen your understanding and enhance your problem-solving skills.
| Resource | Description | Access |
|---|---|---|
| Official College Board Materials | These include sample problems and released questions from past years. They offer an accurate representation of the format and difficulty. | Available on the College Board website |
| Online Learning Platforms | Websites like Khan Academy or AP Classroom provide structured lessons, quizzes, and problems specifically designed for high-level assessments. | Free access through educational accounts |
| Textbooks and Review Books | Many review books offer full-length tests along with detailed solutions to help reinforce concepts and problem-solving techniques. | Available in bookstores or online retailers |
| Study Groups and Forums | Collaborating with peers in study groups or on online forums can provide diverse perspectives on solving problems and tackling tough questions. | Access through online educational communities |
Tracking Your Progress During Preparation
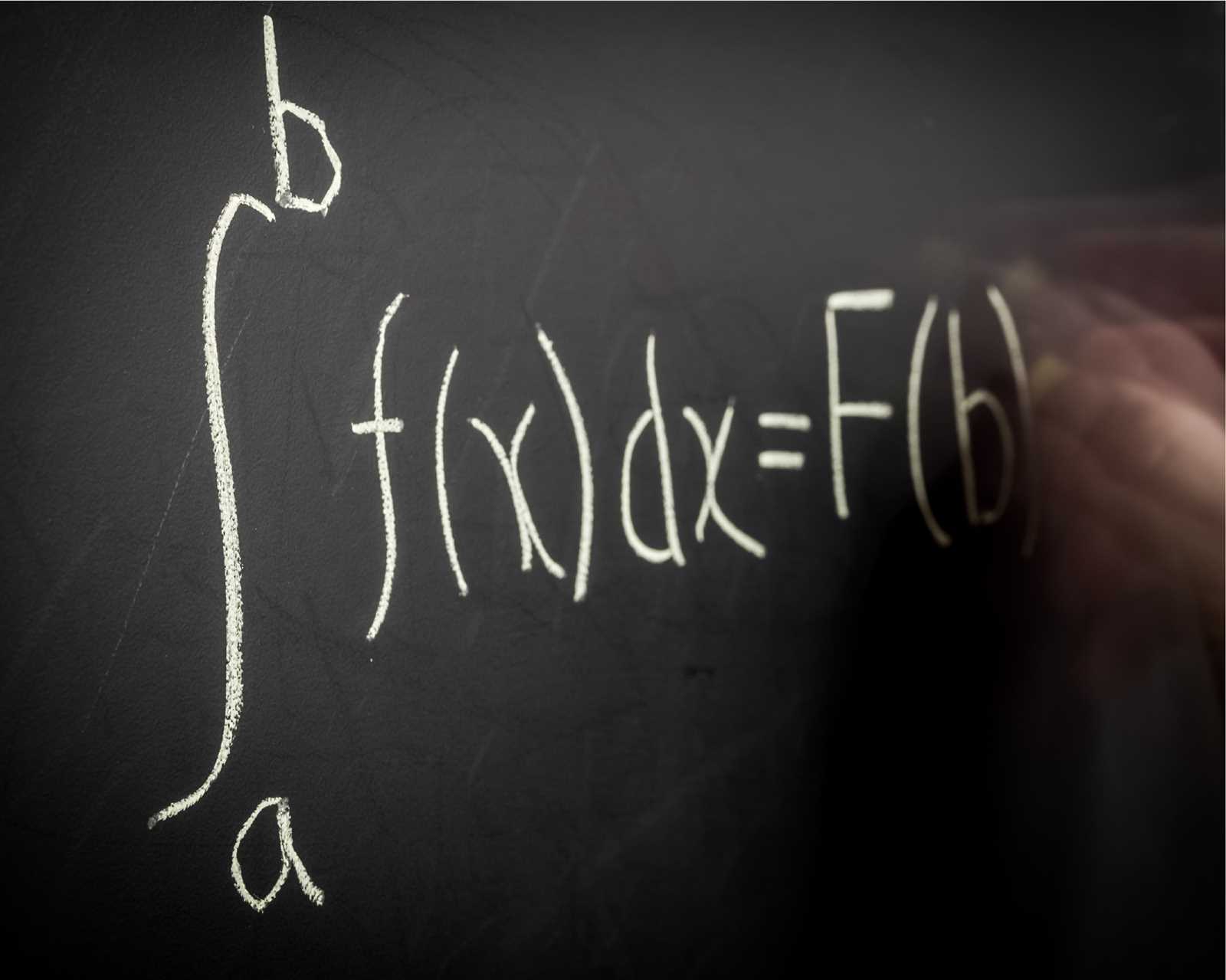
Staying on top of your development throughout the study period is essential for achieving success. By consistently monitoring your understanding of key concepts and problem-solving abilities, you can identify areas that require further focus and fine-tuning. Implementing a system to track your growth helps you ensure that you’re prepared for any challenges that may arise on the day of the test.
- Set Clear Goals: Start by defining specific objectives for each study session. Whether it’s mastering a particular topic or solving a set number of problems, clear targets will help keep you on track.
- Use a Study Calendar: Schedule regular check-ins and allocate time for reviewing past material. Tracking your time spent on each topic will ensure you’re covering all areas.
- Track Problem Solving: Keep a record of the types of problems you’ve worked through. Take note of the ones that were challenging, and review them to reinforce weak points.
- Assess Understanding: Regularly test yourself with mock questions or problems. Compare your results over time to see if you’re making consistent progress.
By organizing your study sessions and keeping a close eye on your progress, you ensure that each session builds upon the last, making your preparation more efficient and effective.