Precalculus Final Exam Study Guide for Success

Achieving success in advanced mathematics requires a solid understanding of key principles that are essential for solving complex problems. This section is designed to help you reinforce your knowledge and ensure you’re well-prepared for the challenges ahead. Whether it’s algebraic equations, geometric shapes, or trigonometric identities, mastering these topics is critical for advancing in your studies.

With focused practice and strategic review, you can confidently approach challenging problems and apply your knowledge effectively. By breaking down the core concepts and reinforcing your skills, you’ll be equipped to tackle each section with confidence. Emphasizing problem-solving techniques and conceptual understanding, this approach will guide you toward better performance and a deeper grasp of the material.

Precalculus Final Exam Study Guide

Achieving proficiency in advanced mathematics requires a clear grasp of fundamental concepts and the ability to apply them to various problems. This section will help you revisit essential principles that are crucial for tackling more complex equations and scenarios. By focusing on the core areas that are most likely to appear in assessments, you can strengthen your understanding and improve your problem-solving abilities.

Throughout this overview, you’ll focus on mastering the key elements such as functions, trigonometry, algebraic manipulation, and graphing techniques. Working through these concepts systematically will not only prepare you for tests but also enhance your ability to approach similar problems in the future with confidence. Repetition, practice, and deep understanding are the cornerstones of mastering this material.

Key Topics to Review

To ensure readiness for any assessment, it’s essential to focus on the core areas that form the foundation of mathematical problem-solving. These fundamental concepts are frequently tested and require a clear understanding and practice to apply them effectively in different scenarios. Below are the key topics to concentrate on for a comprehensive review.

Functions: Understand various types of functions, their properties, and how to manipulate them algebraically and graphically.
Equations: Review methods for solving linear, quadratic, and higher-degree equations, as well as systems of equations.
Graphing Techniques: Be familiar with graphing different equations, including those of polynomials, rational functions, and trigonometric curves.
Trigonometry: Master key identities, solving trigonometric equations, and understanding applications of sine, cosine, and tangent.
Exponential and Logarithmic Functions: Understand how to solve equations involving exponents and logarithms and their real-world applications.
Sequences and Series: Know how to identify, write, and sum arithmetic and geometric sequences.
Complex Numbers: Review how to perform operations with complex numbers and solve equations involving them.
Conic Sections: Understand the properties of parabolas, ellipses, hyperbolas, and circles, and how to analyze their equations.

By focusing on these areas, you will be well-prepared to tackle any problem that arises and be able to approach the material with greater confidence and ease.

Essential Formulas for Precalculus

Having a solid grasp of key formulas is essential for solving complex mathematical problems efficiently. These expressions serve as tools to simplify calculations and enable quick problem-solving in various topics, from algebra to trigonometry. In this section, we will review some of the most frequently used formulas that are crucial for mastering the subject.

Algebraic and Polynomial Formulas

Understanding the basic algebraic rules and formulas is foundational to solving equations and simplifying expressions. Some important formulas to remember include:

Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a
Sum and Difference of Cubes: a³ – b³ = (a – b)(a² + ab + b²)
Factoring Techniques: Recognize patterns such as (a + b)(a – b) = a² – b² and use them to factor expressions quickly.

Trigonometric Formulas

Trigonometry is a key area that requires memorizing several fundamental identities. These formulas simplify solving problems involving angles and periodic functions:

Pythagorean Identity: sin²θ + cos²θ = 1
Double Angle Identity: sin(2θ) = 2sin(θ)cos(θ)
Sum of Angles: sin(A ± B) = sinAcosB ± cosAsinB

By mastering these formulas, you’ll be able to tackle a wide range of problems with greater speed and accuracy.

Understanding Functions and Graphs

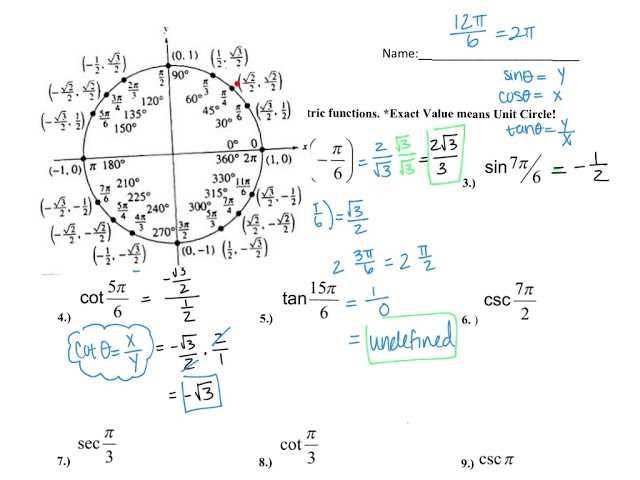
In mathematics, understanding how variables interact with each other is essential for solving problems and analyzing real-world scenarios. Functions serve as a way to represent these relationships, and their graphical representations help visualize how one quantity changes in relation to another. Grasping the connection between equations and their graphs is crucial for mastering complex topics.

Types of Functions

Functions can take various forms, each with its own unique properties and characteristics. Some key types to focus on include:

Linear Functions: Represented by a straight line, these functions show a constant rate of change.
Quadratic Functions: These functions form parabolas and model scenarios involving acceleration or deceleration.
Exponential Functions: Characterized by rapid growth or decay, often seen in real-life applications such as population growth or radioactive decay.

Graphing Techniques

Graphing is a powerful tool for understanding the behavior of functions. Key strategies to keep in mind include:

Identifying Key Points: Plot points such as intercepts, vertices, and asymptotes to build an accurate graph.
Understanding Symmetry: Recognize whether a graph is symmetric, which helps in predicting its shape and behavior.
Transformations: Learn how horizontal and vertical shifts, stretches, and reflections affect the appearance of a graph.

By mastering these concepts, you can confidently analyze and graph various types of functions, a skill that will be invaluable for solving problems in more advanced mathematical fields.

Trigonometric Identities and Applications

Trigonometry plays a vital role in various fields, from physics to engineering, by providing the tools to analyze relationships involving angles and distances. At the core of this subject lie trigonometric identities, which simplify complex expressions and enable efficient problem-solving. Mastering these identities and understanding their applications is essential for progressing in mathematics.

Key Trigonometric Identities

Several fundamental identities are essential for simplifying trigonometric expressions and solving equations. Some of the most important ones include:

Pythagorean Identity: sin²θ + cos²θ = 1 – A foundational identity used to simplify trigonometric expressions.
Sum and Difference Formulas: sin(A ± B) = sinAcosB ± cosAsinB – Useful for finding the sine or cosine of angle sums or differences.
Double Angle Identities: sin(2θ) = 2sin(θ)cos(θ) – These identities help in simplifying and solving trigonometric equations.

Applications of Trigonometry

Trigonometric functions are not only useful for solving equations but also have practical applications in various real-world problems:

Wave Patterns: Trigonometric functions, especially sine and cosine, model periodic behaviors such as sound waves and light waves.
Angles of Elevation and Depression: These concepts are applied in navigation, architecture, and physics to calculate angles in relation to horizontal lines.
Triangular Geometry: Trigonometry is crucial for solving problems involving right triangles, including finding unknown side lengths and angles using the sine, cosine, and tangent ratios.

By mastering these identities and understanding their real-world applications, you will be equipped to solve a wide range of trigonometric problems effectively and confidently.

Mastering Polynomials and Rational Expressions

Understanding how to work with polynomial and rational expressions is crucial for solving a wide range of mathematical problems. These expressions often appear in algebraic equations, and mastering them enables you to simplify, manipulate, and solve complex problems more efficiently. Whether you are factoring polynomials or simplifying rational functions, these skills are foundational for advancing in mathematics.

Polynomials are expressions consisting of terms with variables raised to various powers, while rational expressions involve the ratio of two polynomials. Learning how to factor polynomials, simplify rational functions, and solve related equations is key to mastering this area. The ability to recognize patterns, apply relevant techniques, and perform arithmetic operations is essential for success.

Key strategies to focus on include:

Factoring Polynomials: Recognize common factoring methods such as factoring by grouping, difference of squares, and trinomial factoring.
Simplifying Rational Expressions: Cancel out common factors from the numerator and denominator to simplify expressions.
Solving Polynomial Equations: Use techniques such as synthetic division, long division, and the rational root theorem to find solutions.
Identifying Asymptotes in Rational Functions: Understand how vertical and horizontal asymptotes are determined based on the degree of the polynomials.

By mastering these techniques, you’ll be able to approach polynomial and rational expression problems with greater confidence and accuracy, making them easier to tackle in various contexts.

Complex Numbers and Their Operations

Complex numbers expand the realm of mathematics by allowing for the inclusion of solutions to equations that cannot be solved with just real numbers. These numbers are composed of both a real and an imaginary part, offering a new way to approach certain types of algebraic problems. Understanding their structure and learning how to perform operations with them is essential for solving problems in higher-level mathematics and engineering.

Structure of Complex Numbers

A complex number consists of two parts: a real part and an imaginary part. The general form of a complex number is written as a + bi, where a is the real part, and b is the coefficient of the imaginary unit i, where i is defined as the square root of -1. Working with complex numbers involves performing operations such as addition, subtraction, multiplication, and division, which are similar to operations with real numbers but include the imaginary unit.

Operations with Complex Numbers

Just like real numbers, complex numbers can be added, subtracted, multiplied, and divided. Below are the key operations to focus on:

Addition and Subtraction: Combine like terms by adding or subtracting the real parts and the imaginary parts separately. Example: (a + bi) + (c + di) = (a + c) + (b + d)i
Multiplication: Multiply complex numbers by distributing each term and applying the identity i² = -1. Example: (a + bi)(c + di) = ac + adi + bci + bdi² = (ac – bd) + (ad + bc)i
Division: To divide complex numbers, multiply both the numerator and denominator by the conjugate of the denominator to eliminate the imaginary part from the denominator. Example: (a + bi) / (c + di) = ((a + bi)(c – di)) / (c² + d²)

Mastering these operations will allow you to solve equations and work with complex numbers more effectively, whether in abstract algebra, physics, or other advanced fields.

Logarithms and Exponential Functions

Exponential functions and their inverses, logarithms, are fundamental concepts in mathematics that model growth, decay, and many other natural phenomena. These functions allow us to solve equations involving exponential growth or shrinking processes, such as population growth, radioactive decay, and financial modeling. Understanding the properties and operations of both logarithmic and exponential functions is essential for solving a wide range of mathematical problems.

Exponential functions involve expressions where the variable appears as an exponent, typically in the form a^x, where a is a constant base and x is the exponent. The inverse of an exponential function is a logarithmic function, written as log_a(x), which helps us determine the exponent needed to achieve a certain value when the base is raised to a power. These functions are interconnected and often used together to solve real-world problems involving rates of change and scaling.

Key concepts to focus on include:

Properties of Exponential Functions: Recognizing the rapid growth or decay that occurs with increasing exponents. Common examples include f(x) = a^x, where a > 1 represents exponential growth and 0 represents exponential decay.
Logarithmic Properties: The properties of logarithms allow for the simplification of complex equations. These include the product rule, quotient rule, and power rule, which simplify expressions involving logarithmic functions.
Solving Exponential Equations: Techniques for solving equations where the variable appears in the exponent. This often involves taking the logarithm of both sides to isolate the variable.
Solving Logarithmic Equations: Using the inverse relationship between logarithms and exponentials to solve for unknowns in logarithmic expressions.

By mastering the relationship between logarithmic and exponential functions, you’ll be able to solve a variety of mathematical and real-world problems more effectively and confidently.

Preparing for Word Problems

Word problems can seem daunting at first, but with the right approach, they can be broken down into manageable steps. The key to solving these types of problems is translating real-world scenarios into mathematical expressions or equations. Once you can identify the variables and relationships involved, solving the problem becomes a matter of applying the appropriate mathematical techniques.

The first step is to carefully read and understand the problem. Look for important details, such as what is being asked, the quantities involved, and any constraints or conditions that must be considered. Then, determine what type of mathematical model best represents the situation. This could involve algebraic equations, geometric formulas, or functions, depending on the context of the problem.

Key strategies for solving word problems include:

Identify the unknowns: Clearly define what you’re solving for and assign variables to those unknowns.
Translate the problem: Convert the words and phrases into mathematical expressions or equations. Pay attention to key terms such as “total,” “difference,” “product,” and “ratio,” which indicate specific operations.
Set up an equation: Use the relationships and formulas that apply to the problem to create an equation. This could involve linear equations, quadratic equations, or systems of equations, depending on the complexity of the problem.
Solve and check: After solving for the unknowns, check your solution to ensure it makes sense within the context of the problem. Always verify that your answer satisfies the conditions given in the problem.

With practice, you’ll develop the skills to approach word problems with confidence and solve them efficiently, no matter how complex they may seem at first.

Solving Systems of Equations

Solving systems of equations involves finding values for variables that satisfy multiple equations simultaneously. These problems often arise in various contexts, such as determining the intersection points of lines or finding solutions to problems with multiple constraints. The goal is to identify values for the unknowns that work for all equations in the system.

There are several methods available for solving these types of problems, each suitable for different situations. The most common approaches include substitution, elimination, and graphical methods. Each technique has its strengths depending on the form of the system and the complexity of the equations involved.

Methods for solving systems include:

Substitution Method: This approach involves solving one equation for one variable and then substituting that expression into the other equation. This reduces the system to a single equation with one unknown, which can be solved directly.
Elimination Method: In this method, you add or subtract the equations to eliminate one of the variables. This simplifies the system, allowing you to solve for the remaining variable. Once you find one solution, substitute it back into one of the original equations to find the other variable.
Graphical Method: By graphing both equations on the same coordinate plane, you can visually determine the point(s) where the equations intersect. The coordinates of the intersection point(s) provide the solution to the system.

When dealing with more complex systems, such as those with more than two equations or variables, matrix methods and other advanced techniques can be used. Regardless of the method, the key to solving these problems effectively is careful manipulation of the equations and logical reasoning to isolate the unknowns.

Limit Concepts and Techniques

The concept of a limit is a fundamental idea in calculus that describes how a function behaves as its input approaches a certain value. It is essential for understanding continuity, derivatives, and integrals. Limits allow us to make sense of situations where a function might not be directly computable at a specific point, yet its behavior near that point can still provide valuable information.

Limits are used to describe both finite values and asymptotic behavior, such as approaching infinity. Mastering the techniques for calculating limits is essential for solving problems involving rates of change and curve analysis. Several methods exist for evaluating limits, including direct substitution, factoring, rationalization, and L’Hopital’s rule.

Common techniques for evaluating limits include:

Method	When to Use	Description
Direct Substitution	When the function is continuous at the point	Simply substitute the value of the variable into the function.
Factoring	When direct substitution results in an indeterminate form	Factor the numerator and denominator to cancel common factors, then substitute.
Rationalization	When dealing with square roots or irrational expressions	Multiply both the numerator and denominator by the conjugate to simplify the expression.
L’Hopital’s Rule	When encountering 0/0 or ∞/∞ indeterminate forms	Differentiate the numerator and denominator and then evaluate the limit.

Understanding these techniques helps in solving limits more efficiently, especially when approaching problems that involve complex rational functions or indeterminate forms. Practicing these methods will enhance your ability to handle a wide range of problems involving limits.

Derivatives and Their Significance

The concept of a derivative is central to understanding how quantities change with respect to one another. It measures the rate at which a function’s value changes as its input changes, providing insight into the function’s behavior and its instantaneous rate of change. This is particularly useful for analyzing motion, growth, and optimization problems, where understanding the rate of change is crucial.

Derivatives have a wide range of applications in various fields, from physics to economics. They help in finding the slope of curves, determining maximum or minimum values, and modeling real-world phenomena such as velocity, acceleration, and population growth. The significance of derivatives extends beyond simple rates of change, providing essential tools for analyzing dynamic systems.

Key aspects of derivatives include:

Instantaneous Rate of Change: The derivative provides the rate at which a quantity changes at a specific point, rather than over an interval.
Slopes of Tangent Lines: The derivative represents the slope of the tangent line to a curve at any given point, showing how steep the curve is at that location.
Critical Points: By setting the derivative equal to zero, we can find critical points where the function may have maxima, minima, or inflection points.
Optimization: Derivatives help in finding optimal solutions to problems, such as maximizing profit or minimizing cost.

Mastering derivatives is essential for analyzing the behavior of functions and solving real-world problems that involve rates of change. Whether it’s finding velocity, understanding trends, or optimizing solutions, the derivative is an indispensable tool for making sense of change.

Analyzing Sequences and Series

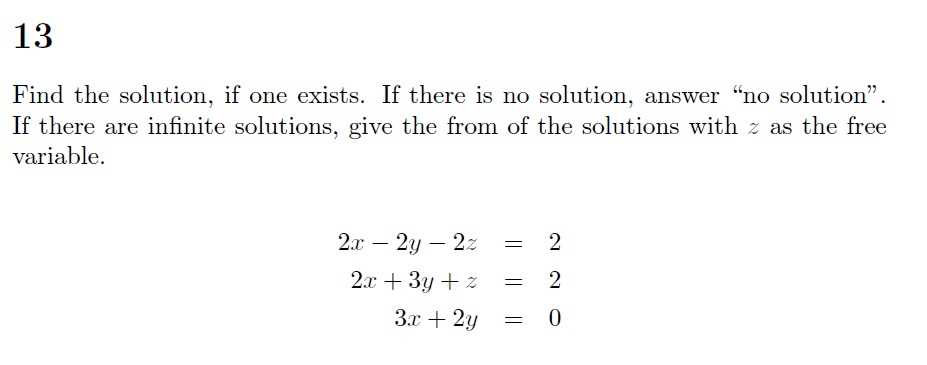
Understanding sequences and series is essential for analyzing patterns and making predictions based on those patterns. A sequence is an ordered list of numbers, where each term has a specific relationship with the previous term. A series, on the other hand, is the sum of the terms in a sequence. By examining both, we can gain valuable insights into the behavior of numerical patterns, whether they are arithmetic, geometric, or more complex.

These mathematical concepts are widely used in various fields, from computing to finance, and are essential for solving problems that involve repeated processes or cumulative sums. Analyzing sequences and series allows us to identify key properties such as convergence, divergence, and closed-form expressions for summing terms.

Key concepts when working with sequences and series:

Type	Description	Formula
Arithmetic Sequence	A sequence where the difference between consecutive terms is constant.	aₙ = a₁ + (n – 1) * d
Geometric Sequence	A sequence where each term is obtained by multiplying the previous term by a constant ratio.	aₙ = a₁ * r^(n – 1)
Arithmetic Series	The sum of the terms of an arithmetic sequence.	Sₙ = n/2 * (2a₁ + (n – 1) * d)
Geometric Series	The sum of the terms of a geometric sequence.	Sₙ = a₁ * (1 – rⁿ) / (1 – r) for \|r\|

By mastering these techniques, you can easily identify the sum of a sequence, find missing terms, and understand the behavior of long sequences and series. Whether you’re working with a simple arithmetic sequence or a more complex geometric series, the tools for analyzing them are indispensable in mathematical analysis.

Conic Sections: Circles and Parabolas

Conic sections represent curves that are formed by the intersection of a plane and a cone. Two of the most fundamental conic sections are circles and parabolas. These shapes are central to understanding the geometry of curves and have wide applications in fields such as physics, engineering, and architecture. Whether describing planetary motion or the trajectory of a projectile, the properties of circles and parabolas are invaluable for solving real-world problems.

Circles and parabolas each have unique characteristics that make them distinct. A circle is defined by a set of points that are all equidistant from a central point, while a parabola is a curve that can be described by a quadratic equation. Both shapes exhibit symmetry and are described by simple, elegant equations, making them a crucial part of mathematical study.

Key characteristics of circles and parabolas:

Shape	General Equation	Key Features
Circle	(x – h)² + (y – k)² = r²	Center (h, k), radius r
Parabola	y = ax² + bx + c	Vertex, axis of symmetry, focus, directrix

Understanding these conic sections requires familiarity with their geometric properties and their algebraic equations. For a circle, the distance from the center to any point on the curve remains constant, while for a parabola, the curve opens either upwards or downwards, depending on the value of the coefficient ‘a’. These basic concepts lay the foundation for more complex analysis and applications.

Vectors and Matrices Review

In the realm of mathematics, vectors and matrices are essential tools that allow us to represent and solve a wide range of problems, especially in fields like physics, engineering, and computer science. These mathematical structures help to describe quantities with direction and magnitude (vectors), as well as organize data or represent linear transformations (matrices). Gaining a strong understanding of vectors and matrices is critical for solving problems that involve multidimensional spaces and systems of equations.

Vectors are typically used to represent quantities that have both direction and magnitude, such as velocity or force. Matrices, on the other hand, are rectangular arrays of numbers that are used to perform various operations, such as rotations, translations, and scaling, or to represent systems of linear equations. Understanding how to perform arithmetic operations with these structures is a key skill in algebra and geometry.

Key Concepts to Review:

Vector Operations: Addition, subtraction, dot product, cross product
Matrix Operations: Addition, multiplication, transpose, inverse
Linear Systems: Solving systems of equations using matrices (Gaussian elimination, matrix inversion)
Determinants: How to calculate the determinant of a matrix and its significance in solving linear systems
Applications: Using vectors and matrices in real-world problems (such as physics, computer graphics, and economics)

Understanding vector and matrix operations is not only about manipulating numbers, but also about interpreting their meanings in practical contexts. For instance, vectors are used to model directions and magnitudes in physical systems, while matrices can represent the coefficients of equations or transformations in multi-dimensional spaces. By reviewing the fundamentals of both topics, you will be better prepared to tackle more complex problems and applications.

Key Tips for Time Management

Effective time management is a vital skill that can help individuals stay organized, reduce stress, and improve productivity. Whether you are preparing for an important task or working through a series of challenges, being able to allocate your time wisely is crucial to achieving success. Having a structured approach to managing your time can help ensure that you stay focused, make progress, and meet deadlines efficiently.

By planning ahead, prioritizing tasks, and avoiding procrastination, you can maximize your time and accomplish more in less time. This section outlines essential strategies that can help you stay on track and optimize your performance, no matter the task at hand.

Effective Planning Strategies

Create a Schedule: Break down your tasks into manageable chunks and set deadlines for each step.
Set Priorities: Focus on the most important and time-sensitive tasks first to make the best use of your time.
Use Time Blocks: Set specific time intervals for focused work and break times to prevent burnout.

Techniques to Stay Focused

Avoid Distractions: Minimize distractions by turning off notifications or working in a quiet environment.
Practice the Pomodoro Technique: Work for a set period (e.g., 25 minutes), followed by a short break to recharge.
Track Progress: Keep track of your progress to stay motivated and make adjustments if necessary.

By incorporating these time management techniques into your routine, you can improve your productivity and reduce the anxiety that often comes with tight deadlines. Prioritizing and organizing tasks efficiently will help you work smarter, not harder, ultimately leading to greater success.

Practice Test Strategies

Taking practice assessments is a crucial part of preparation. These exercises not only help reinforce knowledge but also allow you to familiarize yourself with the format and types of questions that may appear. Effective practice sessions can enhance both your confidence and performance. By using the right strategies, you can maximize the benefits of these mock tests and better gauge your readiness.

Here are several strategies to make the most out of your practice assessments:

Pre-Test Preparation

Set Clear Goals: Before starting a practice test, identify what you aim to achieve, such as improving speed or mastering specific topics.
Simulate Test Conditions: Take the practice test under the same time limits and environment as the real situation to build focus and reduce test anxiety.
Review Relevant Material: Focus on areas where you feel less confident and ensure you are prepared for a range of question types.

During the Test

Manage Time Wisely: Keep track of time to ensure you have enough opportunity to answer all questions. If stuck, move on and return later if necessary.
Read Instructions Carefully: Pay attention to any specific instructions for each section or question to avoid mistakes.
Stay Calm: Stay composed even if you encounter difficult questions. Take deep breaths and tackle them methodically.

Post-Test Review

Analyze Mistakes: Carefully review incorrect answers to understand your mistakes and identify areas for improvement.
Track Progress: Keep a record of your scores and track improvements over time to adjust your preparation accordingly.
Seek Feedback: If possible, discuss difficult questions with a teacher or peer to gain a deeper understanding of the material.

Incorporating these strategies will allow you to approach practice assessments with a focused and constructive mindset. With consistent effort and careful review, your preparedness and confidence will significantly improve.

Final Day Preparation

On the day of the assessment, being fully prepared extends beyond the material you’ve studied. It’s important to focus on practical details that will help you perform at your best. How you approach the day can have a significant impact on your concentration, confidence, and overall performance. Below are key steps to ensure you are ready for the challenge ahead.

Morning Routine

Get a Good Night’s Sleep: A full night of rest is crucial. Aim for at least 7–8 hours of sleep to ensure your mind is clear and alert.
Eat a Nutritious Breakfast: Opt for a balanced meal with protein, complex carbs, and healthy fats to provide sustained energy throughout the day.
Stay Hydrated: Drink water in the morning, but avoid overconsumption right before the assessment to prevent frequent bathroom breaks.

Before the Assessment

Review Key Concepts: Lightly skim over your notes, focusing on areas that are critical or challenging, but avoid cramming.
Organize Your Materials: Double-check that you have everything you need: pens, pencils, erasers, a calculator (if allowed), and any other required items.
Arrive Early: Aim to arrive at the testing location with plenty of time to spare, so you can settle in and reduce any last-minute stress.

During the Assessment

Stay Calm: Take deep breaths if you start to feel anxious. Keeping a calm mindset helps maintain focus.
Read Each Question Carefully: Take your time to fully understand what is being asked before you start solving. Look for key words that hint at specific strategies or concepts.
Manage Your Time: Pace yourself throughout the test. Don’t spend too much time on any one question. Move on if necessary and come back to it later.

After the Assessment

Reflect on Your Performance: Once the assessment is over, take a moment to reflect on what went well and where you can improve in future challenges.
Relax: Take some time to unwind and reward yourself for completing the task, regardless of the outcome.

By following these steps, you ensure that you are not only well-prepared in terms of knowledge but also in terms of mindset and logistics. Approaching the day with confidence and a calm demeanor will help you achieve your best results.