AP Statistics Chapter 12 Test Answers Explained

In this section, we explore essential principles that are critical for understanding and solving complex problems related to data interpretation. The focus is on developing a deeper understanding of how to approach and analyze various types of numerical information and their implications. By grasping these concepts, students can enhance their problem-solving abilities and approach challenges with confidence.

Effective preparation for this part of the course requires a solid foundation in reasoning and interpreting different patterns found in data. It’s important to not only understand how to perform calculations but also to recognize the broader meaning behind the numbers. The process involves applying logical thinking to break down intricate scenarios into manageable pieces.

Success in this area comes with practice and a thorough understanding of the methods. Mastering these skills will allow students to confidently navigate through challenges and improve their performance in related exercises. The ability to draw meaningful conclusions from data is a valuable skill that extends beyond academic tests and into real-world applications.

How to Approach Chapter 12 Test Questions

When facing complex questions that involve data analysis and interpretation, it’s important to adopt a structured approach. This method will help break down each question into manageable steps, ensuring a clear path to the correct solution. The goal is to understand the underlying principles before jumping into calculations or conclusions.

Step-by-Step Process

Read Carefully: Begin by reading each question thoroughly to understand the context and what is being asked. Pay attention to keywords that indicate the type of analysis needed.
Identify Key Elements: Break down the problem by identifying the essential components, such as data points, variables, and any specific conditions or requirements.
Choose the Right Approach: Decide which method or formula is best suited for solving the problem based on the information given. Different types of questions may require different techniques.
Perform Calculations: Carry out the necessary computations carefully. Double-check each step to avoid errors.

Effective Strategies for Success

Practice Regularly: Consistent practice with similar problems will improve your ability to recognize patterns and solve questions faster.
Time Management: Allocate a specific amount of time to each question and move on if you get stuck. This prevents you from spending too much time on one problem.
Review Your Work: After completing a question, review your solution to ensure it is consistent with the problem’s requirements and that no steps were skipped.

Key Concepts in AP Statistics Chapter 12

Understanding the fundamental principles of data analysis is crucial for tackling complex problems in this section. The concepts explored here focus on interpreting various types of data and drawing meaningful conclusions from them. Emphasis is placed on developing skills to identify patterns, assess relationships, and make inferences based on numerical information.

Central to this section is the understanding of how to work with data sets in ways that allow for effective decision-making. You will learn to identify trends and assess the significance of results, using both theoretical knowledge and practical techniques. Mastery of these core concepts will help you approach problems with confidence and clarity, ensuring a more accurate analysis in future challenges.

Additionally, the ability to choose the appropriate analytical tools for a given problem is emphasized. By gaining experience with different methods, you’ll be equipped to address questions that range from basic interpretation to more complex, multi-step calculations.

Mastering Hypothesis Testing in Statistics

Hypothesis testing is a critical skill that allows you to make decisions based on data. This process involves evaluating the validity of a claim or assumption about a population by analyzing sample data. Mastery of this concept enables you to determine whether the evidence supports a hypothesis or if the claim should be rejected.

Understanding the Process

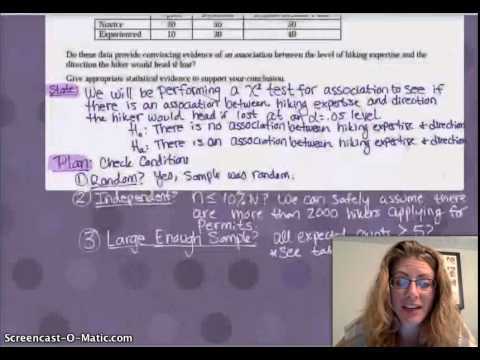
Begin with a clear hypothesis: Define both the null and alternative hypotheses. The null hypothesis typically represents the status quo, while the alternative hypothesis proposes a change or difference.

Collect and analyze data: After setting up the hypotheses, gather relevant data from a sample that can be analyzed to test the hypothesis. Choose the appropriate test based on the data type and the nature of the hypothesis.

Key Considerations for Accuracy

Significance Level: Decide on a significance level (usually 0.05), which defines the threshold for rejecting the null hypothesis.
P-Value: The p-value tells you how much evidence you have against the null hypothesis. A smaller p-value indicates stronger evidence to reject the null hypothesis.
Power of the Test: The power of a test refers to its ability to detect a true effect when it exists. Understanding this helps you choose an effective test for your data.

Understanding Data Distribution and Analysis

Data analysis begins with an understanding of how values are distributed within a given dataset. By examining this distribution, we can draw meaningful conclusions about trends, patterns, and outliers. A clear grasp of data distribution helps in making accurate predictions and informed decisions, which are essential for any type of analysis.

Types of Data Distribution

Different datasets follow different patterns of distribution, each providing insights into the behavior of the data. Below are some common types of distributions:

Distribution Type	Description
Normal Distribution	Data is symmetrically distributed, with most values clustered around the mean.
Skewed Distribution	Data is not symmetrical, with a tail on one side of the mean.
Bimodal Distribution	Two distinct peaks are present in the data.
Uniform Distribution	Data values are evenly spread across the range of values.

Key Techniques for Analyzing Data

To analyze data effectively, it’s essential to use the right tools and techniques. Some of the most widely used methods include:

Descriptive Statistics: Summarizes data with measures like mean, median, mode, range, and standard deviation.
Data Visualization: Graphs like histograms, box plots, and scatter plots offer visual insights into the distribution.
Inferential Analysis: Drawing conclusions about a population based on sample data, using methods like confidence intervals and hypothesis tests.

Effective Techniques for Exam Preparation

Successfully preparing for an exam requires a strategic approach that focuses on understanding key concepts and practicing problem-solving techniques. The right study habits and resources can make a significant difference in achieving desired results. It is essential to organize study time effectively, ensuring that each topic is thoroughly reviewed and that practice is focused on areas of weakness.

Key Strategies for Success

Start Early: Begin studying well in advance to allow plenty of time to understand the material and review it multiple times.
Use Practice Materials: Practice with past exams and sample questions to familiarize yourself with the format and types of problems you may encounter.
Identify Weak Areas: Focus on areas where you struggle the most, and spend extra time reviewing those topics to strengthen your knowledge.
Study Actively: Engage in active learning techniques, such as summarizing information, teaching concepts to others, or solving practice problems without looking at the solutions.
Join Study Groups: Collaborate with peers to discuss difficult topics, share insights, and test each other’s understanding.

Time Management Tips

Efficient time management can significantly enhance your ability to absorb and retain information. Consider the following tips:

Create a Study Schedule: Set specific study goals and allocate time for each topic. Stick to the schedule as closely as possible to avoid cramming.
Break Study Sessions into Intervals: Use the Pomodoro Technique (study for 25 minutes, then take a 5-minute break) to maintain focus and avoid burnout.
Avoid Multitasking: Concentrate on one task at a time to improve efficiency and comprehension.

Common Pitfalls in Statistical Calculations

When working with data and performing various types of calculations, it is easy to make mistakes that can lead to incorrect conclusions. Common errors often arise from misinterpretation of formulas, improper data handling, or overlooking essential steps in the calculation process. Understanding these potential pitfalls can help avoid costly mistakes and improve accuracy in the analysis.

Common Errors in Data Handling

Forgetting to Account for Outliers: Failing to identify and properly manage outliers can skew results, leading to inaccurate conclusions.
Incorrect Data Entry: Simple typographical errors or incorrect data input can result in major discrepancies in final calculations.
Assuming a Normal Distribution: Automatically assuming that data follows a normal distribution without checking can lead to misleading results, especially in tests that rely on this assumption.
Overlooking Missing Data: Ignoring missing or incomplete data can distort findings. It’s important to know how to handle missing values appropriately.

Calculation Mistakes to Watch For

Improper Use of Formulas: Using the wrong formula or applying it incorrectly is a common mistake, particularly when dealing with complex calculations.
Misinterpretation of Results: Failing to interpret results in the correct context can lead to wrong conclusions, especially when dealing with hypothesis testing or confidence intervals.
Rounding Errors: Over-rounding numbers during intermediate steps can cause small inaccuracies that accumulate over time.

Exploring Confidence Intervals for Data

Confidence intervals offer a range of values that estimate an unknown parameter, providing a sense of the reliability of the data and analysis. They are a powerful tool to express uncertainty and make inferences about a population based on sample data. Understanding how to construct and interpret these intervals is crucial for evaluating the precision of estimates in any analytical context.

Constructing a Confidence Interval

To build a confidence interval, the first step is to gather sample data and calculate the sample mean and standard deviation. Next, the margin of error is determined, which involves selecting a confidence level (such as 95% or 99%) and using the appropriate z or t value for that level. The final interval is constructed by adding and subtracting the margin of error from the sample mean.

Interpreting Confidence Intervals

Range of Possible Values: The interval provides a range in which the true population parameter is likely to fall, given the sample data.
Level of Confidence: A higher confidence level results in a wider interval, indicating a higher degree of certainty but also more variability.
Precision vs. Confidence: While increasing the confidence level enhances certainty, it reduces precision. Balancing these factors is essential when choosing an appropriate interval for analysis.

Interpreting Results from Statistical Tests

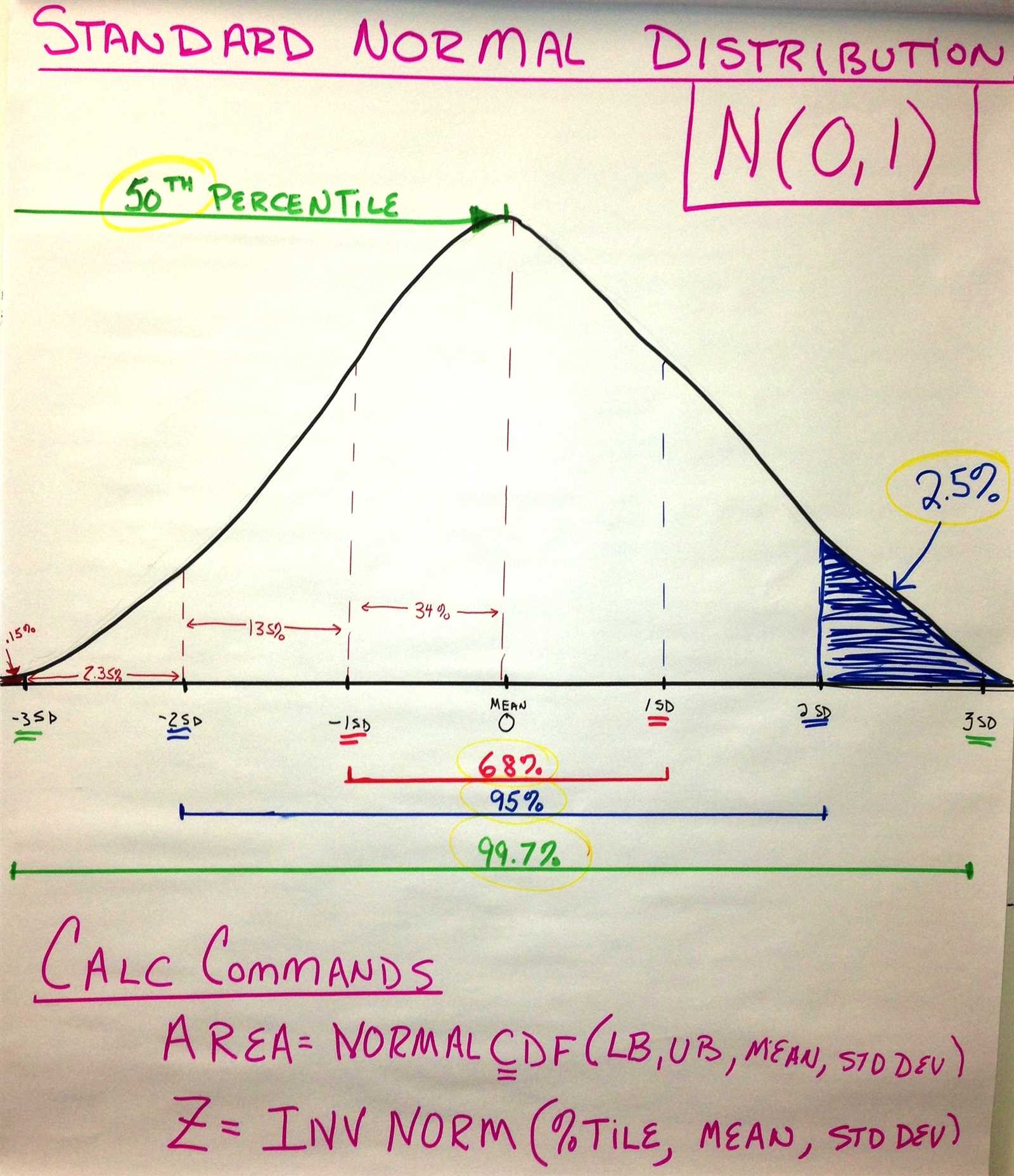
Interpreting the outcomes of a statistical evaluation is a vital step in drawing meaningful conclusions from the data. The results offer insights into whether observed patterns are likely to be real or if they could have occurred by chance. Understanding the components of these results, such as p-values, confidence intervals, and effect sizes, is crucial for making informed decisions based on the analysis.

Understanding the P-Value

The p-value is a key component in determining whether a result is statistically significant. It represents the probability of observing the data, or something more extreme, assuming the null hypothesis is true. A smaller p-value suggests stronger evidence against the null hypothesis, typically leading to rejection of the null hypothesis if it falls below a predetermined threshold (often 0.05).

Confidence Intervals and Significance

Confidence intervals provide a range of plausible values for the population parameter based on the sample data. If the confidence interval for a parameter does not contain the value specified by the null hypothesis, it provides further evidence against the null hypothesis. This helps in confirming whether the observed effect is meaningful and not due to random variation.

Effect size complements p-values by quantifying the magnitude of the observed effect, offering a clearer picture of practical significance. Even with a small p-value, the effect size can determine whether the result is substantial enough to matter in real-world scenarios.

How to Analyze Statistical Problem Scenarios

When approaching a problem involving data analysis, it is essential to break down the scenario into manageable steps. Start by identifying the question being asked and the type of data involved. Understanding the context and the goals of the analysis will help guide the choice of appropriate methods and tools to use. By clearly defining the variables and their relationships, you can develop a clear strategy to analyze and interpret the information effectively.

Identifying the Key Variables

The first step in analyzing a problem is recognizing the variables that play a role in the scenario. These may include independent and dependent variables, and sometimes confounding factors that could affect the results. Defining these variables allows you to focus on what is being measured and how each factor might influence the outcomes.

Choosing the Right Analytical Approach

Once you have a clear understanding of the variables involved, selecting the appropriate analytical approach is crucial. Different types of problems require different techniques, such as comparing means, assessing relationships, or evaluating proportions. It’s important to choose methods that align with the data type and the research questions to ensure accurate interpretations and conclusions.

After deciding on the approach, it is essential to check for assumptions or conditions that may affect the validity of the chosen methods. Proper execution of these techniques, coupled with clear interpretations, will lead to a well-rounded understanding of the data in the problem scenario.

Practical Applications of Chapter 12 Theories

Understanding and applying the concepts from this section can provide valuable insights in real-world scenarios. The theories explored in this section are not just academic exercises; they offer practical tools for making data-driven decisions across various fields. By applying these methods, one can gain deeper insights into trends, behaviors, and relationships, leading to more informed conclusions and strategies.

Applications in Business

In the business world, the ability to analyze and interpret data effectively is crucial for success. Here are some practical ways these theories can be used:

Market Research: Identifying customer preferences, predicting trends, and improving products based on data analysis.
Risk Management: Assessing financial risk, forecasting potential market fluctuations, and ensuring business stability.
Operational Efficiency: Optimizing processes, reducing waste, and improving productivity through data insights.

Applications in Healthcare

The healthcare industry can greatly benefit from these concepts, especially in areas where data analysis is critical for improving patient care and operational outcomes:

Clinical Trials: Determining the effectiveness of new treatments and medications through hypothesis testing.
Patient Outcomes: Analyzing patient data to predict outcomes and improve care strategies.
Health Policy: Informing policy decisions by analyzing data trends in disease spread, healthcare access, and more.

By using the theories covered in this section, professionals in various fields can apply these techniques to solve practical problems, make evidence-based decisions, and optimize processes.

Improving Test Performance with Practice

Consistent practice is essential for mastering any subject, especially when dealing with complex concepts that require critical thinking. The more you engage with problems and scenarios, the more familiar you become with the patterns and techniques needed to succeed. Practicing regularly helps reinforce your understanding and enhances your problem-solving skills, ultimately leading to better performance on assessments.

Effective preparation doesn’t just involve reviewing material but actively applying it through practice exercises. This method ensures that you not only memorize information but also understand how to use it in different contexts. By simulating exam conditions, you can increase your confidence and reduce test anxiety, making it easier to perform under pressure.

Benefits of Practice

Here are some of the key benefits of incorporating regular practice into your study routine:

Benefit	Explanation
Enhanced Understanding	Repetition helps reinforce concepts and improves comprehension.
Faster Problem Solving	Frequent practice enables quicker recognition of solution patterns and strategies.
Confidence Boost	Regular practice builds familiarity and reduces uncertainty when faced with similar problems.
Improved Retention	Revisiting material regularly strengthens long-term memory and recall ability.

By dedicating time to practice, you ensure that you are not only prepared but confident in your ability to tackle any challenge. Whether through problem sets, mock exams, or reviewing past materials, the more you practice, the more proficient you will become.

Strategies for Understanding Statistical Significance

Grasping the concept of statistical significance is crucial for interpreting the results of any analytical process. It helps determine whether observed results are likely due to chance or if they represent a meaningful relationship. By mastering key strategies, you can better assess the validity and relevance of your findings in various contexts.

Understanding when results are statistically significant allows you to make informed decisions and draw accurate conclusions. It also aids in distinguishing between random variations and true effects in your data. Several approaches can help clarify the concept, making it more accessible and easier to apply in real-world scenarios.

Key Strategies for Understanding Statistical Significance

Below are some essential techniques for grasping and applying the idea of statistical significance:

Familiarize with Hypothesis Testing: Hypothesis testing involves comparing observed results to a predefined threshold to determine if they are significant. Understanding this process is the first step in evaluating whether results are meaningful.
Master the p-value: The p-value helps you measure the likelihood that the observed results occurred by chance. A smaller p-value typically indicates a stronger significance, with values below a certain threshold (e.g., 0.05) often considered statistically significant.
Understand Confidence Intervals: Confidence intervals give you a range within which the true value is likely to fall. A narrower interval suggests more precise estimates, helping you assess the significance of results.
Consider the Sample Size: The larger the sample size, the more reliable the conclusions. Small sample sizes can lead to unreliable results, even if they appear statistically significant.

Common Misconceptions

Several common misconceptions can lead to confusion when interpreting statistical significance:

Statistical significance equals practical significance: Just because a result is statistically significant doesn’t mean it has real-world importance or impact.
Smaller p-value means stronger evidence: While a smaller p-value indicates that the observed results are less likely due to chance, it doesn’t guarantee the findings are meaningful or substantial.
Failure to reject the null hypothesis means the effect is null: Not rejecting the null hypothesis doesn’t necessarily prove there is no effect; it simply means there isn’t enough evidence to support a significant relationship.

By applying these strategies, you can improve your ability to evaluate the significance of results accurately, leading to more reliable conclusions in any analytical process.

Data Interpretation Tips for AP Statistics

Effectively interpreting data is essential for drawing accurate conclusions from any set of information. In any analytical field, it’s important to recognize patterns, trends, and anomalies within datasets, which will help you make informed decisions. Whether you’re evaluating graphs, tables, or raw data, using the right strategies can enhance your ability to extract meaningful insights.

Here are some tips to help improve your data interpretation skills:

Focus on Context: Understanding the context in which the data was collected is crucial for interpreting its relevance. Always consider the source, purpose, and limitations of the dataset before drawing conclusions.
Examine Key Trends: Look for overarching patterns in the data. Whether it’s a steady increase, sharp decline, or periodic fluctuation, identifying trends can guide your analysis and help highlight significant results.
Pay Attention to Outliers: Outliers can significantly impact your interpretation, potentially skewing results or suggesting false trends. Be sure to assess whether outliers are due to errors, or if they provide meaningful information.
Understand the Distribution: The way data is distributed (e.g., normal, skewed, uniform) affects how it should be analyzed. Knowing the distribution helps you decide which methods and techniques to apply.
Use Appropriate Visuals: Visual aids like histograms, box plots, and scatter plots are powerful tools for interpreting data. They can reveal trends, relationships, and anomalies more clearly than raw numbers alone.

Example Table for Data Interpretation

Category	Frequency
Category A	25
Category B	40
Category C	15
Category D	10

By using these tips and tools, you can develop a more precise and systematic approach to interpreting data. This helps you make better-informed decisions and accurately assess patterns and relationships in your findings.

Steps to Avoid Errors During Exams

When facing an examination, it’s crucial to approach the process with a clear mindset and organized strategy. Mistakes often occur due to mismanagement of time, overlooking instructions, or failing to focus on the most important aspects of a question. By following a set of structured steps, you can minimize the likelihood of errors and maximize your performance during exams.

Here are some key steps to help you avoid common mistakes:

Read Instructions Carefully: Take the time to thoroughly read the instructions before starting any section. Skipping over details can lead to incorrect responses or missing vital information.
Manage Your Time: Allocate a specific amount of time to each question or section. Keeping track of time ensures that you don’t rush through important questions and can complete everything within the allotted period.
Double-Check Your Work: Always leave time to review your answers. Even small errors in calculations or wording can cost valuable points.
Stay Focused: Concentrate on one question at a time. Avoid distractions and maintain focus throughout the exam to ensure that your answers are precise and relevant.
Understand the Question: Make sure you fully understand what is being asked. If necessary, rephrase the question in simpler terms to ensure that you’re addressing the correct task.

By following these steps, you’ll be better equipped to tackle the challenges of any exam and reduce the risk of unnecessary mistakes. Preparation, focus, and time management are key factors that contribute to your success.

Building Statistical Knowledge for Success

Developing a strong foundation in data analysis and interpretation is essential for achieving success in any related field. Mastering the core principles, techniques, and tools will enable individuals to approach problems with confidence and draw meaningful conclusions from various data sets. A structured and gradual approach to learning enhances understanding and allows for effective application in real-world situations.

Key steps to build a solid foundation for success include:

Understand the Fundamentals: Start by grasping the basic concepts. Building a strong understanding of core principles sets the stage for more advanced topics.
Consistent Practice: Regularly solving problems and applying concepts helps reinforce learning and improve problem-solving skills.
Engage with Real-World Examples: Analyzing practical examples helps bridge the gap between theory and real-world applications, making the learning process more meaningful.
Seek Feedback: Collaborating with peers and seeking guidance from instructors allows for a deeper understanding and correction of misconceptions.
Stay Curious: Cultivate a mindset of curiosity and continuously explore new topics and methods that can enhance your knowledge and skills.

By focusing on these strategies, individuals can build a robust knowledge base, ensuring long-term success and growth in their field of interest.

Preparing for Complex Problem Solving

Approaching complex problems requires a methodical and strategic mindset. These types of challenges often involve multiple steps, detailed analysis, and a deep understanding of concepts. Effective preparation focuses on developing the ability to break down difficult questions into manageable parts and apply appropriate techniques to solve them efficiently.

Key Strategies for Tackling Complex Problems

Understand the Core Concepts: Ensure a solid grasp of the underlying principles before attempting difficult questions. This foundation will help navigate through complex issues.
Practice with Varied Examples: Exposing yourself to a range of problems, from straightforward to challenging, will develop problem-solving flexibility and reinforce learning.
Break Down the Problem: Decompose complex problems into smaller, easier-to-manage components. This simplifies the task and makes it less overwhelming.
Review Mistakes: Take time to analyze errors. Understanding why something went wrong is crucial for improving and avoiding the same mistakes in the future.
Time Management: Allocate sufficient time for each problem, but also know when to move on. Time pressure can lead to mistakes if you’re stuck on a single issue.

Additional Tips for Effective Problem Solving

Stay Calm and Focused: A clear and focused mind is key when dealing with intricate problems. Avoid rushing through and ensure each step is carefully considered.
Work in Stages: Set achievable milestones for each stage of problem-solving. Completing smaller tasks one by one helps build confidence and ensures accuracy.
Collaborate: If possible, discuss complex problems with peers or mentors. Multiple perspectives can often shed light on different approaches and solutions.

By following these strategies, you can prepare yourself to confidently approach and solve even the most complex problems, leading to better performance and understanding.