
For students navigating through advanced mathematical concepts, having a reliable resource to guide through problem-solving can make a significant difference. The complexity of equations and functions can be daunting, but with proper tools and support, mastering these topics becomes more achievable. This section provides essential resources and strategies for tackling common challenges faced during this level of study.
With detailed solutions and clear explanations, learners can gain a deeper understanding of how to approach various problems. Whether you’re struggling with quadratic equations, functions, or graphing, these solutions aim to simplify the learning process. Building a strong foundation in these areas will not only help with current coursework but also prepare you for more advanced mathematical studies in the future.
By breaking down complex ideas into manageable steps, students can approach each topic with confidence, making the journey through higher-level math more structured and less overwhelming. With consistent practice and the right support, mastering these concepts becomes a rewarding and empowering experience.
Ple Platoweb Algebra 2 Answers Overview
Mathematical courses at the advanced level can present students with a variety of challenges. Understanding key concepts and applying them correctly is crucial for success. This section focuses on the resources and techniques that can help students tackle difficult problems efficiently. By utilizing structured support, learners can improve their problem-solving skills and master essential mathematical topics.
Key Concepts and Problem Types
To succeed in this level of mathematics, students must become familiar with several core concepts. These topics often include:
- Functions and their applications
- Equations involving multiple variables
- Quadratic equations and their solutions
- Graphing and interpreting data
- Polynomials and rational expressions
How to Maximize Learning and Performance

To get the most out of available resources, students should:
- Break down problems into smaller, manageable steps.
- Practice regularly to strengthen understanding.
- Review solutions to understand the reasoning behind each step.
- Ask for clarification on areas that seem confusing.
- Utilize practice materials to reinforce learning.
By adopting these strategies, students can confidently work through challenges and build a strong mathematical foundation. With consistent effort and the right tools, mastering these concepts becomes not only possible but also rewarding.
Mastering Algebra 2 with Online Resources
Accessing online platforms can significantly enhance the learning experience for students facing advanced mathematics. With the right digital tools, learners can build a deeper understanding of challenging concepts and practice problem-solving at their own pace. Online resources provide interactive ways to reinforce material, track progress, and offer immediate feedback, making them an invaluable tool for mastering complex topics.
Interactive Tools and Practice Exercises
Online platforms often provide interactive exercises that help students grasp key concepts more effectively. Some of the most useful tools include:
- Step-by-step problem solvers
- Video tutorials for visual learners
- Practice quizzes and tests for self-assessment
- Graphing tools for visualizing equations
Tracking Progress and Improving Skills
One of the advantages of using online resources is the ability to monitor progress over time. These platforms typically offer:
- Instant feedback to identify areas for improvement
- Progress reports to track strengths and weaknesses
- Personalized learning paths to target specific skills
By consistently using these online tools, students can refine their mathematical abilities and build the confidence necessary to tackle advanced topics effectively.
Key Concepts in Algebra 2 Explained
In advanced mathematics, understanding core principles is essential for tackling more complex problems. Grasping foundational ideas enables students to approach each topic with confidence. This section will break down some of the most important concepts in higher-level math, providing clear explanations and examples to help reinforce understanding.
Key areas of focus often include:
- Functions: Understanding how different types of functions behave and how to manipulate them.
- Quadratic Equations: Solving equations that involve variables raised to the second power.
- Polynomials: Breaking down expressions involving powers of variables and simplifying them.
- Rational Expressions: Learning how to work with fractions that involve variables.
- Exponential and Logarithmic Functions: Exploring the relationship between these functions and their applications.
By mastering these topics, students can build a solid mathematical foundation, allowing them to move on to more advanced topics with ease. A clear understanding of these concepts is critical for success in future coursework and real-world applications.
Understanding the Importance of Practice
Mastering complex mathematical topics requires consistent effort and repetition. Practice plays a pivotal role in solidifying knowledge, as it allows students to internalize concepts, recognize patterns, and develop problem-solving skills. Through regular practice, learners not only improve their accuracy but also build the confidence needed to tackle more challenging problems.
The Role of Repetition in Learning
Repetition helps reinforce key concepts and methods. The more problems a student solves, the more familiar they become with the various techniques needed to address different types of equations and functions. Key benefits include:
- Improved speed and accuracy in solving problems.
- Enhanced ability to recognize patterns in different problems.
- Increased confidence in handling a variety of problem types.
Effective Practice Strategies
To make the most of practice sessions, students should:
- Focus on a variety of problems to gain exposure to different techniques.
- Take time to review solutions and understand the reasoning behind each step.
- Challenge themselves with progressively more difficult problems.
By incorporating these strategies into their study routine, students can accelerate their learning and gain a deeper understanding of the material.
Effective Strategies for Solving Problems
Addressing complex mathematical challenges requires a clear approach and systematic techniques. Developing an effective problem-solving strategy helps streamline the process, minimizes errors, and boosts confidence. By breaking tasks into manageable steps and focusing on key methods, students can overcome difficulties more efficiently.
Breaking Down Problems into Steps
One of the most effective ways to approach difficult problems is to simplify them. Breaking them into smaller parts ensures clarity and provides a structured path to the solution. Key steps include:
- Carefully read the problem to understand what is being asked.
-
Effective Strategies for Solving Problems
Addressing complex mathematical challenges requires a clear approach and systematic techniques. Developing an effective problem-solving strategy helps streamline the process, minimizes errors, and boosts confidence. By breaking tasks into manageable steps and focusing on key methods, students can overcome difficulties more efficiently.
Breaking Down Problems into Steps
One of the most effective ways to approach difficult problems is to simplify them. Breaking them into smaller parts ensures clarity and provides a structured path to the solution. Key steps include:
- Carefully read the problem to understand what is being asked.
- Identify known variables and relationships between them.
- Plan an approach using relevant methods or formulas.
- Work through the problem step by step, checking accuracy at each stage.
- Verify the final solution to ensure it satisfies the original question.
Common Techniques for Success
To solve problems effectively, consider utilizing the following strategies:
- Draw diagrams or graphs to visualize relationships.
- Substitute simpler values to test hypotheses.
- Break formulas into their basic components for easier understanding.
- Practice with similar problems to recognize patterns and methods.
- Review errors to avoid repeating mistakes.
By adopting these strategies, students can tackle even the most challenging tasks with confidence and achieve consistent success in their studies.
Common Mistakes to Avoid in Algebra 2
As students work through advanced mathematical problems, they often encounter pitfalls that can hinder their progress. Recognizing and avoiding these common errors is essential for mastering the material. Understanding where mistakes typically occur can help students sharpen their problem-solving skills and improve their overall performance.
Overlooking Key Details
One of the most frequent mistakes is failing to pay attention to critical details in the problem. Missing out on important information can lead to incorrect answers or misinterpretation of the question. Common oversights include:
- Not properly identifying the type of equation or function involved.
- Forgetting to simplify expressions before solving.
- Neglecting to check the units or constraints given in the problem.
Incorrect Application of Formulas
Another common error is misapplying formulas or using the wrong method to solve a problem. Students may remember a formula but fail to adapt it correctly to the problem at hand. This can be avoided by:
- Reviewing the conditions under which a formula is applicable.
- Double-checking the steps before jumping to conclusions.
- Rewriting the formula to ensure all variables are accounted for.
By being mindful of these common pitfalls and taking a more careful approach, students can avoid errors and enhance their understanding of the material. Consistent practice and attention to detail will lead to improved accuracy and confidence in solving problems.
Step-by-Step Guide to Algebra 2 Solutions
Solving complex mathematical problems becomes much more manageable when approached systematically. A step-by-step method allows students to break down each challenge into smaller, more manageable parts, ensuring a clear path to the solution. This guide outlines the general process for approaching and solving a variety of advanced problems.
Each problem can be tackled more effectively by following these structured steps:
- Read and Understand the Problem: Begin by carefully reading the problem and identifying the given information and what needs to be solved. Pay attention to keywords and any constraints or conditions specified.
- Organize the Information: Identify all the variables and constants. Write down the equation or expression clearly, ensuring that you understand the relationships between the different elements of the problem.
- Choose the Appropriate Method: Decide which approach or formula is best suited for the problem. This could involve solving equations, factoring, or using functions based on the type of question.
- Work Through the Steps: Apply the chosen method step by step. If the problem involves multiple steps, ensure that each calculation is correct before moving to the next. Show all your work clearly for easier review.
- Double-Check Your Solution: Once a solution is reached, review each step to verify the accuracy of your calculations. Ensure that the solution satisfies all the conditions of the problem.
By following this approach, students can increase their chances of finding accurate solutions while building their problem-solving skills. Consistent practice with these steps will lead to improved performance and confidence in handling more advanced material.
Exploring Advanced Algebra 2 Topics
As students progress in their mathematical studies, they encounter increasingly complex concepts that build on foundational knowledge. These advanced topics require a deeper understanding of mathematical principles and an ability to apply them in more challenging scenarios. This section explores some of the key areas students will face in advanced problem-solving.
- Functions and Their Transformations: Understanding the different types of functions, such as linear, quadratic, exponential, and logarithmic, is crucial. Students learn to manipulate and transform these functions through shifts, stretches, and reflections to solve more complicated equations.
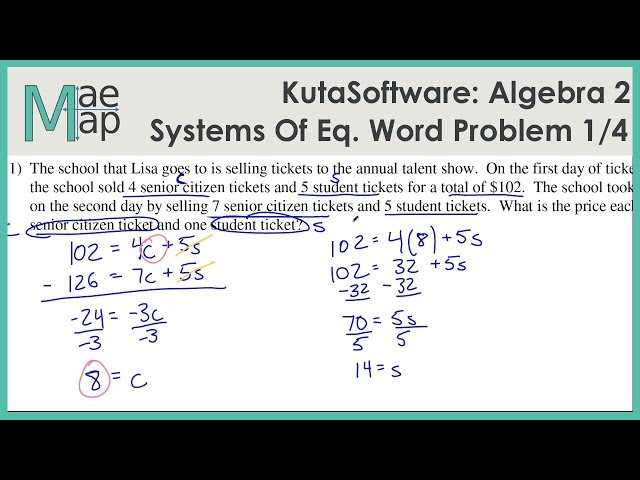
- Systems of Equations: In more advanced problems, students work with systems of equations, where multiple equations are solved simultaneously. These systems can be linear or non-linear, and students must learn various methods, such as substitution and elimination, to find solutions.
- Polynomial Operations: Higher-degree polynomials and their operations become a focus in advanced topics. Students practice factoring, expanding, and simplifying polynomial expressions to solve problems involving complex polynomial equations.
- Rational Expressions and Equations: Rational expressions, which involve fractions with polynomials in the numerator and denominator, are another key concept. Students learn to simplify, multiply, divide, and solve equations involving rational expressions.
- Radicals and Rational Exponents: An important part of advanced studies is working with square roots, cube roots, and other radical expressions. Students also explore rational exponents and learn to simplify and manipulate these types of expressions.
By mastering these advanced topics, students develop critical thinking skills and improve their ability to solve more complex mathematical challenges. Consistent practice and application of these concepts lead to a greater understanding of how mathematical principles work in real-world situations and more abstract contexts.
Tips for Preparing for Algebra 2 Tests
Effective preparation is essential for performing well on exams, especially when tackling complex mathematical concepts. By developing a strategy that incorporates understanding the material, practicing regularly, and utilizing effective study methods, students can increase their confidence and improve their performance. This section offers helpful tips to guide you through the preparation process.
Review Key Concepts
Start by revisiting the fundamental principles that will appear on the test. Focus on the main topics, such as functions, equations, and graphing. Break the material down into manageable sections, and make sure to understand each topic before moving on to the next one. Create a summary sheet with important formulas and concepts to refresh your memory before the exam.
Practice, Practice, Practice
One of the most effective ways to prepare is through practice. Solve various types of problems that you may encounter on the test. This will help reinforce your understanding of concepts and improve problem-solving speed. Work through sample tests or use online resources to access practice questions and check your answers for accuracy.
In addition, make sure to review any mistakes made during practice. Understanding where you went wrong and correcting those errors will enhance your problem-solving skills. The more you practice, the more comfortable you will become with the material, which will boost your performance during the test.
Utilize Available Resources
Don’t hesitate to use resources like textbooks, online tutorials, and study groups to clarify any doubts. If you’re struggling with a particular topic, consider seeking extra help from a tutor or asking your instructor for guidance. Understanding complex topics becomes much easier when you approach them from different angles.
By combining these strategies, students can effectively prepare for their exams and feel confident in their ability to tackle any questions that come their way. Consistent practice, understanding key concepts, and using available resources will ensure that you are well-prepared and ready to succeed on test day.
Understanding Functions and Equations
Mathematical expressions often represent relationships between different quantities. Functions and equations are two essential tools for capturing these relationships, allowing for a structured approach to solving problems. By understanding how one value relates to another through a function or how two expressions balance out in an equation, individuals can make sense of complex situations and derive solutions more efficiently.
Functions: Mapping Inputs to Outputs
A function defines how each input corresponds to exactly one output. This relationship is essential for modeling real-world scenarios, from simple calculations to more complex patterns. Functions can be represented in various forms such as graphs, equations, or tables, each offering a unique perspective on how different values interact.
Equations: Solving for Unknowns
Equations are used to express relationships where two expressions are set equal to each other. The goal is to determine the unknown variable(s) that make both sides of the equation true. Understanding how to manipulate and solve equations is a crucial skill in mathematics, as it applies to numerous fields, including physics, economics, and engineering.
Type of Equation General Form Example Linear Equation ax + b = c 2x + 5 = 11 Quadratic Equation ax² + bx + c = 0 x² – 5x + 6 = 0 Exponential Equation y = ab^x y = 3(2)^x Through mastering functions and equations, individuals gain a deeper understanding of mathematical relationships, allowing them to solve complex problems with ease. These concepts are foundational not only in academic mathematics but also in real-life applications.
Solving Quadratic Equations with Ease
Quadratic equations are a key component of mathematics, and learning how to solve them efficiently opens doors to solving a variety of problems. These equations often appear in areas such as physics, engineering, and economics. Understanding the methods to find their solutions is essential for anyone looking to master mathematical concepts. With a few different techniques available, it becomes easier to find the roots of these types of expressions.
One of the most common ways to solve a quadratic equation is by using the quadratic formula. This method provides a straightforward path to finding the solutions, whether the roots are real or complex. Other methods, such as factoring or completing the square, also offer valuable techniques, depending on the specific equation at hand.
The Quadratic Formula
The quadratic formula is a universal method that applies to all quadratic equations. It is given by:
x = (-b ± √(b² – 4ac)) / 2a
Where ‘a’, ‘b’, and ‘c’ are the coefficients from the equation ax² + bx + c = 0. By substituting these values into the formula, the solutions for ‘x’ can be easily calculated.
Factoring

Factoring is another method for solving quadratic equations, but it only works when the equation can be factored into two binomials. This method involves rewriting the quadratic equation as the product of two binomials and then setting each factor equal to zero. This method is quicker but is not always applicable.
By mastering these methods, anyone can confidently solve quadratic equations and apply these techniques to various real-world problems with ease.
Using Graphing to Solve Algebra Problems
Graphing is an essential tool for solving mathematical problems, providing a visual representation of equations and functions. By plotting relationships between variables on a coordinate plane, graphing helps to identify key features of a function, such as solutions, intersections, and trends. This method simplifies complex problems and allows for quicker, more intuitive analysis.
When equations are plotted on a graph, the intersections with the axes or other graphs directly correspond to the solutions of the problem. This visual approach helps to clarify the behavior of the equation and makes it easier to see patterns or significant points, such as maximum or minimum values, without doing lengthy calculations. Whether you’re dealing with linear, quadratic, or exponential equations, graphing can provide clear and immediate insights into the solution.
Graphing Linear Equations
Linear equations are represented by straight lines on a graph. To solve such an equation, you plot the line and look for its intersection with the x-axis. The point where the line crosses the x-axis indicates the solution, or root, of the equation. This method is straightforward and highly effective for solving simple equations quickly.
Graphing Quadratic Equations
Quadratic equations produce parabolas on a graph. By plotting a quadratic equation, you can find its x-intercepts, which are the values of the variable that satisfy the equation. Additionally, the vertex of the parabola gives you important information about the maximum or minimum value of the function, which can be useful for solving optimization problems or understanding the shape and direction of the curve.
Overall, using graphing to solve problems enhances both understanding and problem-solving speed. It allows for a visual grasp of concepts that may otherwise seem abstract, making it a valuable tool in mathematics.
The Role of Variables in Algebra 2
Variables are fundamental components in mathematical expressions, serving as placeholders for unknown values. In advanced mathematical studies, these symbols are used to represent quantities that may change or vary depending on the context. Understanding how variables interact with one another and with constants is crucial for solving complex equations and analyzing relationships between different elements of a problem.
Variables allow mathematicians to create general rules and solve problems without needing specific numbers. They help express relationships that can be applied to multiple situations, making mathematical analysis more versatile and applicable to real-world scenarios. Here’s a closer look at how variables play a critical role:
Key Roles of Variables
- Representing Unknowns: Variables stand in for values that are not yet known, allowing the development of equations that can be solved.
- Defining Relationships: They are used to express relationships between different quantities, such as the connection between the input and output of a function.
- Simplifying Problems: By using variables, complex problems can be simplified into more manageable forms, often making it easier to find solutions through manipulation.
Types of Variables
- Independent Variables: These are the quantities you can control or manipulate. For instance, in an equation representing time versus distance, time would be the independent variable.
- Dependent Variables: These variables depend on the value of the independent variable. In the same equation, the distance would be the dependent variable as it changes in response to time.
Ultimately, variables are essential for structuring equations, solving for unknowns, and understanding the relationships within complex systems. Their role extends beyond simply representing numbers–they provide the tools needed to analyze and manipulate mathematical concepts effectively.
How Algebra 2 Prepares for Advanced Math
The study of mathematical concepts at the intermediate level lays a strong foundation for more complex topics in higher education. By engaging with various problem-solving techniques and exploring advanced relationships between numbers, students develop critical thinking and analytical skills that are essential for mastering higher-level mathematics.
Key topics covered at this level play a significant role in preparing students for more challenging courses, including calculus, statistics, and even advanced engineering mathematics. Understanding these principles provides the necessary framework for tackling the abstract and intricate problems encountered in these fields. Here’s how this stage of learning acts as a stepping stone:
Core Areas of Preparation
- Understanding Functions: Learning the behavior and properties of different functions helps students in studying calculus, where functions are central to concepts like derivatives and integrals.
- Mastering Equations: Solving various types of equations–linear, quadratic, and systems–provides the basis for approaching more complex algebraic structures in higher math courses.
- Working with Polynomials: Polynomials form the backbone of many advanced topics, including the study of polynomials in calculus and their applications in optimization problems.
- Exploring Exponents and Logarithms: The manipulation of exponents and logarithmic functions is essential for understanding topics such as exponential growth and decay in calculus and differential equations.
Building Analytical Skills
- Problem-Solving Techniques: The ability to break down and simplify problems into manageable steps is cultivated at this level, a skill vital for tackling advanced mathematical problems.
- Logical Reasoning: Developing a clear and structured approach to mathematical problems enhances overall logical thinking, crucial for tackling complex problems in upper-level math courses.
By mastering the essential concepts taught at this stage, students are well-equipped to excel in more demanding mathematical studies and to apply these skills in various real-world contexts, whether in engineering, economics, or scientific research.
Why Algebra 2 is Essential for College Prep
Building a strong foundation in mathematics is crucial for preparing for higher education. The concepts learned at this stage go beyond basic operations, equipping students with the necessary problem-solving tools and logical skills that are essential in college courses. Understanding these advanced topics prepares students for more specialized fields of study, such as engineering, economics, and the natural sciences, all of which demand a solid grasp of complex mathematical concepts.
Having a deep understanding of mathematical structures enables students to approach problems with critical thinking and develop the skills necessary for success in both academic and real-world scenarios. Whether analyzing data or formulating hypotheses, these concepts provide the backbone for tackling higher-level challenges in college and beyond.
Key Advantages for College Success
Advantage Impact on Higher Education Critical Thinking Skills Helps students analyze complex problems with a structured approach. Enhanced Problem-Solving Equips students with tools to tackle quantitative challenges in various fields. Understanding Abstract Concepts Prepares students for advanced studies in science, engineering, and economics. Data Interpretation Fosters the ability to analyze and interpret data, a key skill in many disciplines. Application to Advanced College Disciplines
- Engineering: Foundational knowledge in mathematics is essential for solving technical problems.
- Natural Sciences: Skills learned are critical for understanding experimental designs and data analysis in fields like chemistry and physics.
- Economics and Business: Mathematical reasoning aids in analyzing financial trends and understanding market dynamics.
In conclusion, mastering these intermediate mathematical principles is not just about achieving high test scores. It’s about preparing for the intellectual demands of college-level coursework and beyond. A strong grasp of these concepts ensures students are equipped with the analytical mindset and problem-solving skills needed for success in both academic and professional settings.