As you approach the end of the term, it’s essential to prepare thoroughly for your upcoming assessment in mathematics. Mastering core concepts and solving problems efficiently can make a significant difference in your performance. This section will focus on the most important strategies and resources to help you prepare with confidence.
Strengthening your understanding of key mathematical principles is the first step. Whether it’s solving equations, graphing functions, or working with expressions, having a clear grasp of these topics will enable you to tackle various problems with ease. Developing your problem-solving skills is equally crucial for success in any test scenario.
Additionally, practice is a powerful tool in improving both speed and accuracy. By reviewing previous lessons and practicing problems, you’ll become more comfortable with different types of questions. Taking time to understand your mistakes and correcting them is one of the most effective ways to improve. With dedication and the right approach, you can achieve outstanding results.
Mastering Key Concepts in Mathematics
To excel in mathematics assessments, a deep understanding of the foundational principles is crucial. Focus on mastering the essential concepts that form the core of most problems. These concepts not only appear frequently in tests but also serve as building blocks for more advanced topics.
Start with the basics, such as solving simple equations and understanding the relationships between variables. Once you’re comfortable with these, move on to more complex topics, such as working with exponents and manipulating expressions. Having a solid grasp of these fundamentals allows you to approach problems methodically and accurately.
Another important area is graphing functions and interpreting their meaning. Being able to visualize equations and their solutions gives you a strategic advantage, especially when dealing with word problems. Mastering these skills will enable you to confidently navigate through different types of questions and scenarios.
Essential Topics for Mathematics Assessments

To perform well in your upcoming test, it’s essential to focus on the most important areas that will likely appear on the assessment. Mastering these key topics will give you the confidence to tackle various problem types effectively. Concentrate on understanding both the concepts and the problem-solving techniques that are frequently tested.
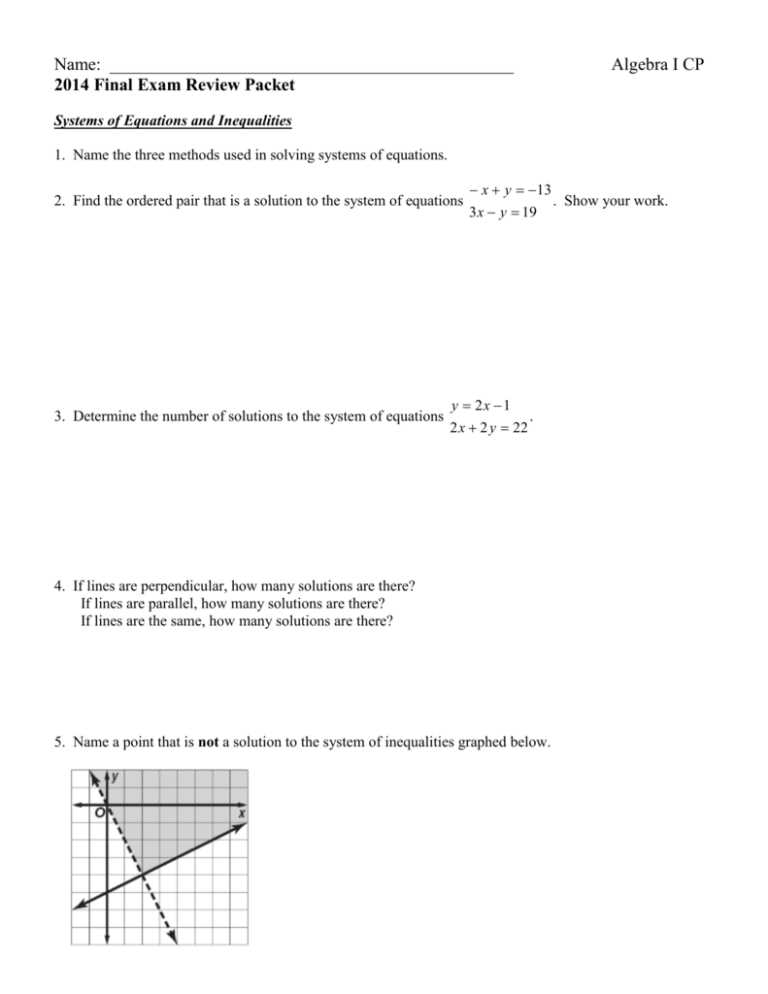
Solving Equations and Inequalities
Being able to solve different types of equations is crucial. This includes linear equations, systems of equations, and inequalities. Practice isolating variables and applying the appropriate operations to both sides of the equation. Strengthening your skills here will ensure that you can solve problems quickly and accurately.
Functions and Graphing
Understanding how to work with functions and graph them is another important area. This includes interpreting linear and quadratic functions, as well as being able to plot points and analyze the relationships between variables. Practice graphing different types of equations and interpreting their behavior to enhance your comprehension and problem-solving ability.
Step-by-Step Approach to Solving Equations
Solving equations requires a clear, methodical approach to ensure accuracy. By following a set of logical steps, you can simplify complex problems and isolate the unknown variable. This structured method makes it easier to solve equations of varying difficulty, from basic linear equations to more complex expressions.
Start by simplifying both sides of the equation whenever possible. Combine like terms and eliminate parentheses. Next, use inverse operations to move terms involving the variable to one side of the equation and constants to the other. Ensure that each step follows a consistent order to maintain balance.
Once the variable is isolated, perform any necessary arithmetic operations to solve for its value. Finally, verify your solution by substituting the value of the variable back into the original equation to ensure both sides are equal. This method will help you approach and solve any equation with confidence and precision.
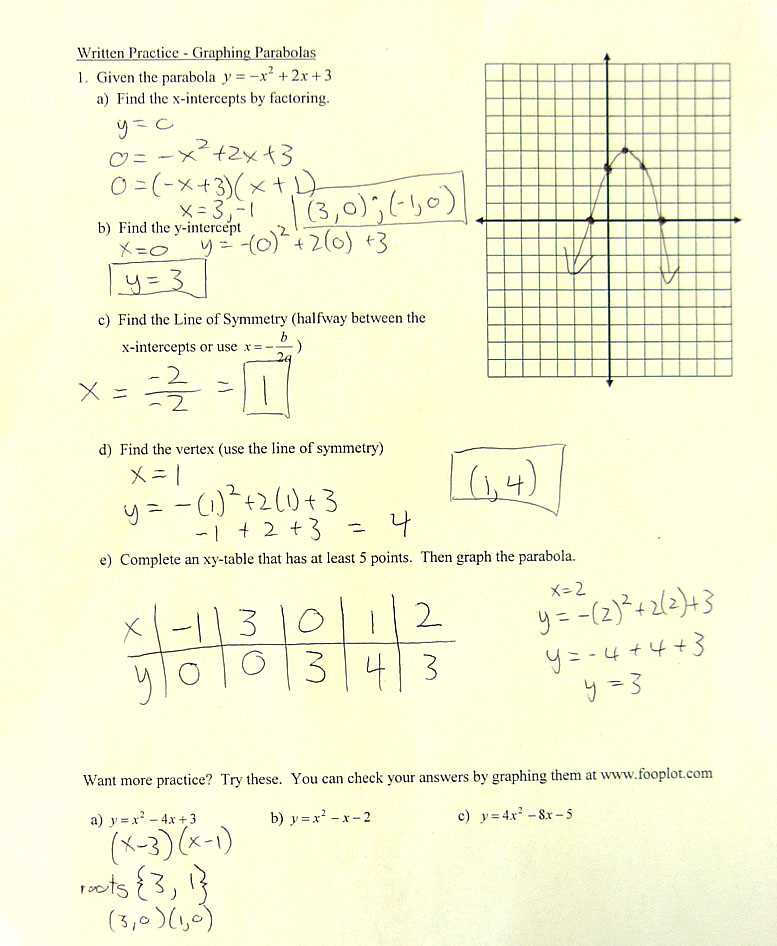
Understanding Linear and Quadratic Functions
Grasping the differences between linear and quadratic functions is essential for solving a wide range of problems. These two types of functions behave differently, and each requires its own method of analysis. By understanding their structure and characteristics, you can easily identify and work with them in various scenarios.
Linear Functions
Linear functions create straight lines when graphed and are defined by the equation y = mx + b, where m is the slope and b is the y-intercept. Key characteristics include:
- The graph is a straight line.
- The slope indicates the steepness of the line.
- The y-intercept represents the point where the line crosses the y-axis.
Quadratic Functions
Quadratic functions, on the other hand, create parabolas when graphed and are defined by the equation y = ax² + bx + c, where a, b, and c are constants. Important points to note include:
- The graph forms a U-shaped curve called a parabola.
- The value of a determines whether the parabola opens upwards or downwards.
- The vertex is the highest or lowest point on the graph.
Understanding these two functions allows you to apply the correct methods for graphing, solving, and analyzing equations in your coursework.
Tips for Solving Word Problems Efficiently
Word problems can often seem overwhelming, but with the right approach, they become much more manageable. The key is to break down the problem into smaller, more digestible parts and systematically translate the words into mathematical expressions. By following a structured approach, you can solve these problems with confidence and accuracy.
Start by carefully reading the problem to understand what is being asked. Identify the important information and the variables involved. Often, highlighting or underlining key facts can help you focus on the most relevant details.
Next, translate the words into equations or expressions. Look for relationships between quantities and determine how they can be mathematically represented. Once the problem is set up, solve it step by step, just like any other equation, ensuring each operation follows logically from the last.
Finally, check your answer to ensure it makes sense in the context of the problem. Ask yourself if the solution is reasonable and if it answers the original question. Practicing these steps regularly will make you more efficient and accurate when tackling word problems.
How to Factor Polynomials Like a Pro
Factoring polynomials can seem challenging at first, but with the right techniques, it becomes an intuitive process. By breaking down complex expressions into simpler binomials or monomials, you can easily identify common factors and simplify problems. Mastering factoring is crucial for solving a variety of mathematical problems efficiently.
Start by looking for the greatest common factor (GCF) across all terms in the polynomial. If a GCF exists, factor it out first to simplify the expression. Once the polynomial is reduced, focus on the remaining terms and apply the appropriate method, such as grouping, using special formulas, or splitting the middle term.
For quadratics, look for patterns that allow you to factor the expression into two binomials. In some cases, you may need to apply the trial-and-error method to identify the correct factor pairs. Practice and familiarity with common patterns will increase your speed and accuracy when factoring polynomials.
Common Mistakes to Avoid in Mathematics
Many students make common errors when solving mathematical problems, often due to oversight or misunderstanding of key concepts. Recognizing these frequent mistakes and understanding how to avoid them can significantly improve your problem-solving skills and accuracy. By staying mindful of these pitfalls, you can prevent simple errors from affecting your performance.
Misapplying Rules of Operations
One of the most common errors is forgetting the proper order of operations or misapplying basic rules. For example, many students mistakenly add or subtract before multiplying or dividing. Always remember the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) to ensure the correct order is followed.
Incorrectly Simplifying Expressions
Another frequent mistake involves incorrect simplification, particularly when dealing with fractions or terms involving exponents. Make sure to carefully combine like terms and follow the proper steps when reducing expressions. Double-checking each step is crucial to avoid losing or miscalculating terms.
| Common Mistake | What to Avoid | How to Correct |
|---|---|---|
| Forgetting to distribute | Incorrectly distributing terms in binomials | Always distribute each term to every term in the parentheses |
| Sign errors | Misplacing or forgetting negative signs | Pay careful attention to signs, especially when adding or subtracting |
| Not checking work | Skipping the verification of solutions | Always substitute the solution back into the original equation to check |
Improving Your Graphing Skills
Graphing is an essential skill for visualizing mathematical relationships and solving problems. The ability to accurately plot points, understand the shape of a graph, and interpret its meaning is crucial for success in many areas of mathematics. By refining your graphing techniques, you will be able to approach problems more efficiently and with greater confidence.
Understanding the Coordinate System
Begin by familiarizing yourself with the coordinate plane. The x-axis and y-axis intersect at the origin (0, 0), and the plane is divided into four quadrants. Knowing how to plot points accurately on this grid is the first step in graphing. Always pay attention to the sign of each coordinate and ensure that you are placing each point in its correct location.
Plotting and Interpreting Functions
Once you understand the basics of plotting points, focus on graphing functions. Start with simple linear equations and gradually move to more complex functions such as quadratics. Remember that the shape of the graph will tell you important information about the function, such as its slope, vertex, and direction of opening. Practice regularly to become comfortable with recognizing these patterns.
Lastly, be sure to use graphing tools or software when available to check your work and visualize more complicated functions. This can help you better understand the relationship between equations and their graphical representations.
Tips for Working with Rational Expressions
Working with rational expressions can be tricky, but with the right approach, it becomes a manageable task. These expressions involve fractions with polynomials in the numerator and denominator, and simplifying or performing operations on them requires careful attention to detail. By mastering a few key techniques, you can improve your accuracy and efficiency when dealing with these types of problems.
Start by factoring both the numerator and the denominator whenever possible. This will help you identify common factors that can be cancelled out, simplifying the expression. Always check for common factors before attempting any addition, subtraction, or multiplication with rational expressions.
When adding or subtracting rational expressions, ensure that the denominators are the same before proceeding. If they are different, find the least common denominator (LCD) and rewrite the expressions accordingly. Multiplying and dividing rational expressions is generally more straightforward, as you simply multiply the numerators and denominators, but always remember to cancel common factors where possible.
Lastly, be cautious of undefined values. Always check the denominator to ensure it doesn’t equal zero, as division by zero is not allowed. Taking these steps will help you solve problems with rational expressions accurately and efficiently.
Mastering Exponents and Radicals
Working with exponents and roots is fundamental to simplifying and solving mathematical expressions. Mastering these concepts will not only streamline your calculations but also allow you to handle more complex problems with ease. The key to success lies in understanding the rules that govern exponents and radicals, and knowing when and how to apply them effectively.
Exponents represent repeated multiplication, while radicals are the inverse operation, representing roots of numbers. Both are essential tools in simplifying expressions and solving equations. It’s important to become familiar with the various exponent rules, such as the product rule, quotient rule, and power of a power rule, to help manage these operations more efficiently.
When working with radicals, remember that square roots, cube roots, and higher-order roots are just special cases of fractional exponents. By converting between radical and exponential form, you can often simplify expressions more easily.
| Operation | Rule | Example |
|---|---|---|
| Multiplying with same base | Keep the base, add the exponents | (x^3 times x^2 = x^5) |
| Dividing with same base | Keep the base, subtract the exponents | (x^5 div x^2 = x^3) |
| Rationalizing the denominator | Multiply numerator and denominator by the radical’s conjugate | (frac{1}{sqrt{2}} = frac{sqrt{2}}{2}) |
Preparing for the Algebra 1 Final Exam

Getting ready for a comprehensive assessment in mathematics requires a strategic approach. Success in these types of evaluations depends on both understanding the core concepts and practicing the application of those principles. The key is to organize your review process and focus on areas that will most likely be tested, while also reinforcing your overall problem-solving skills.
Start by reviewing the major topics covered throughout the course. This will help you identify any areas that need extra attention. Here’s a structured approach to help you prepare:
- Review Key Concepts: Go over the main topics and ensure you understand the foundational principles.
- Practice Problems: Work through a variety of problems, particularly those types you find challenging.
- Use Study Aids: Use textbooks, online resources, and practice tests to supplement your learning.
- Understand the Test Format: Familiarize yourself with the structure of the assessment and the types of questions that are likely to appear.
In addition to reviewing, make sure to stay organized and manage your time effectively. Set aside regular time slots for practice and avoid cramming at the last minute. Consistent preparation, combined with focused practice, will boost your confidence and performance.
- Start Early: Begin preparing well in advance, leaving ample time to go over each topic thoroughly.
- Take Breaks: Short breaks during study sessions will help you stay focused and retain information better.
- Ask for Help: If you’re stuck on a concept, don’t hesitate to ask your teacher or a classmate for clarification.
By following a well-organized study plan and practicing consistently, you can approach your upcoming evaluation with confidence and ensure that you are well-prepared to succeed.
Time Management Strategies for Test Day
On the day of an important assessment, managing your time efficiently is essential to ensure that you can complete all sections and perform at your best. A well-thought-out plan allows you to allocate the right amount of time to each part of the test, helping you stay focused and reducing any feelings of stress. By sticking to a time strategy, you can approach each problem with a clear mind and avoid wasting time on any one question.
Before starting, familiarize yourself with the test’s structure and the total duration available. This understanding will help you pace yourself and prioritize the sections based on their difficulty or the points they carry. Having a strategy in place ensures you do not spend too much time on challenging questions while leaving easier ones unfinished.
Effective Time Allocation Tips
- Understand the Format: Knowing the number of sections and the time allotted for each allows you to plan how long to spend on each type of question.
- Start with the Easiest Questions: Quickly tackle the questions you find easiest to gain momentum and boost confidence early on.
- Don’t Get Stuck: If you encounter a particularly difficult question, move on and return to it later when you’ve made progress in other sections.
- Leave Time for Review: Allocate the last few minutes to go back over your answers, correcting mistakes and filling in any gaps.
Suggested Time Breakdown
Here’s a suggested approach to divide your time effectively: