
Facing an important assessment can be a stressful experience, but with the right approach, you can tackle it confidently. This section is designed to guide you through the essential steps to succeed. We’ll explore strategies for mastering key concepts and solving challenging problems that often appear in these types of evaluations.
Effective preparation is crucial to performing well. By reviewing foundational principles and practicing problem-solving techniques, you’ll enhance your ability to think critically and apply your knowledge under pressure. Understanding how to approach each question strategically is just as important as knowing the material.
In the following sections, you’ll find detailed explanations, step-by-step solutions, and key formulas. These resources will equip you with the tools needed to excel. Whether you’re looking for tips on managing time or advice on avoiding common mistakes, this guide will help you prepare efficiently for the test ahead.
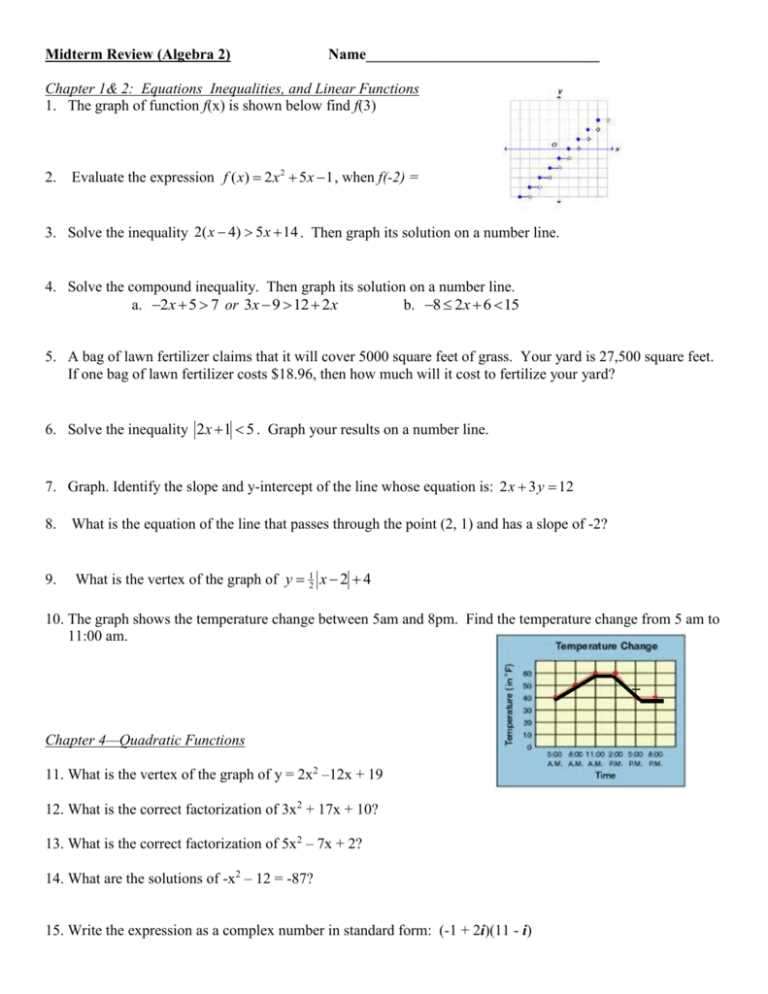
Algebra 2 Midterm Exam with Answers
This section provides a comprehensive guide to help you navigate one of the most challenging assessments in your math journey. By focusing on key topics and offering clear explanations, you’ll be able to tackle complex problems with confidence. Detailed solutions will clarify each step, helping you understand the reasoning behind every calculation and method.
Throughout this guide, you will find carefully selected practice questions that reflect the format and difficulty level typically encountered. These exercises are designed to test your understanding of essential concepts and provide insights into common problem-solving techniques. By working through these problems, you’ll improve both your speed and accuracy, ensuring you’re prepared for any challenges that may arise.
The solutions provided go beyond mere step-by-step instructions. They highlight important strategies for solving problems efficiently and avoiding common pitfalls. With this knowledge, you’ll gain the ability to approach any question logically and find the right answer quickly.
Understanding Algebra 2 Exam Structure

Knowing the layout of the upcoming assessment is essential for proper preparation. Understanding the way questions are organized and what areas will be tested can help you approach the challenge systematically. Typically, this type of evaluation is divided into several sections, each focusing on different mathematical concepts that require a solid understanding and the ability to apply various methods.
The structure often includes a mix of multiple-choice questions, short-answer problems, and more complex problems that require detailed solutions. The variety in question formats means you need to be well-versed in different types of problems and know how to approach them effectively. Time management becomes crucial as you work through the test, as each section has its own level of difficulty and time constraints.
In addition to standard problems, some assessments may feature word problems that require translating real-life situations into mathematical equations. These questions test your ability to think critically and apply abstract concepts to solve practical problems. Preparing for these sections requires both theoretical knowledge and the ability to quickly analyze and interpret data.
Key Topics Covered in Algebra 2
In this section, we explore the fundamental concepts that are essential for understanding the material covered in advanced math assessments. These topics form the foundation for problem-solving and are critical for achieving success in your academic journey. Mastering these areas will provide you with the tools needed to tackle a wide range of challenges efficiently.
Below are the primary areas you should focus on:
- Quadratic Equations – Understanding how to solve, graph, and analyze quadratic functions.
- Polynomials – Operations with polynomials, factoring, and solving polynomial equations.
- Rational Expressions – Simplification, multiplication, division, and solving equations involving rational expressions.
- Exponential and Logarithmic Functions – Understanding their properties and solving equations involving exponents and logs.
- Systems of Equations – Methods for solving systems, including substitution and elimination techniques.
- Sequences and Series – Arithmetic and geometric sequences, summation, and series formulas.
- Conic Sections – Understanding circles, ellipses, hyperbolas, and parabolas and how to graph them.
- Rational Functions – Analyzing and graphing rational functions, including identifying asymptotes and behavior.
These topics are integral to your overall understanding and ability to apply mathematical principles in various contexts. Each area builds upon the previous one, so a strong grasp of earlier concepts will ensure success in solving more complex problems later on.
How to Prepare for Algebra 2 Midterm
Preparing effectively for an important assessment involves a combination of reviewing key concepts, practicing problem-solving techniques, and managing your time wisely. A structured approach to studying will not only help you retain information but also build the confidence needed to tackle various types of questions that may appear.
Organize Your Study Materials
Start by gathering all relevant materials, including textbooks, notes, and past assignments. Organizing your study space will allow you to focus without distractions. Break down the topics you need to review into manageable sections, and prioritize areas where you feel least confident. It’s also helpful to identify which types of problems are most likely to appear and concentrate your efforts on practicing those.
Practice Consistently and Review Mistakes
Working through practice problems regularly is crucial for reinforcing your understanding. Focus on solving problems without looking at solutions first, then check your work to identify any mistakes. Pay special attention to the areas where you struggled, and revisit those concepts until you feel comfortable. Utilizing sample questions that mirror the style and difficulty of the test will give you a better sense of what to expect and help improve your problem-solving skills.
Top Algebra 2 Study Tips
Effective study habits can make all the difference when preparing for a challenging assessment. By adopting the right strategies, you can enhance your understanding, sharpen your problem-solving abilities, and approach the test with confidence. Here are some proven tips that will help you make the most of your study time and maximize your performance.
Break Down Complex Concepts
When dealing with difficult topics, break them down into smaller, more manageable parts. Focus on understanding the fundamentals before attempting complex problems. This method allows you to build a solid foundation, which is essential for tackling more advanced material. Practice problems related to each specific concept before moving on to the next.
Use Active Recall and Spaced Repetition
Rather than passively reading through your notes, engage with the material by testing yourself regularly. Active recall forces you to retrieve information from memory, reinforcing your understanding. Combining this technique with spaced repetition, where you revisit topics at increasing intervals, helps improve long-term retention and ensures that key concepts stay fresh in your mind.
Common Mistakes in Algebra 2 Exams
Many students make avoidable errors during assessments that can significantly impact their scores. These mistakes often stem from misinterpretation of questions, rushed calculations, or overlooking key concepts. By being aware of the most common pitfalls, you can take proactive steps to avoid them and improve your performance.
Common Errors and How to Avoid Them
Here are some frequent mistakes made during assessments and tips for preventing them:
| Mistake | How to Avoid It |
|---|---|
| Forgetting to simplify answers | Always check if your final answer is in its simplest form. |
| Sign errors during calculations | Double-check your signs, especially when working with negative numbers. |
| Misinterpreting word problems | Carefully read the problem and highlight key information before solving. |
| Rushing through complex questions | Take your time to solve each step and review your work before moving on. |
| Skipping over difficult problems | Attempt all problems, but mark challenging ones to come back to later. |
Additional Tips for Success
In addition to avoiding common mistakes, make sure to manage your time effectively during the test. Keep an eye on the clock and pace yourself so that you can address all questions without feeling rushed. Consistent practice and review are essential for recognizing and preventing these errors in future assessments.
Step-by-Step Solutions for Practice Problems
Breaking down problems into smaller, manageable steps is one of the most effective strategies for mastering mathematical concepts. In this section, we will go through detailed solutions for practice questions. These step-by-step explanations will help you understand the reasoning behind each solution and improve your ability to solve similar problems on your own.
The process of solving a problem typically involves identifying the type of question, applying the correct method, and simplifying the solution. By following a structured approach, you can avoid errors and ensure that each step is completed accurately. Below, we provide solutions to several common types of problems:
Example 1: Solving a Quadratic Equation
- Identify the equation format: For example, ax² + bx + c = 0.
- Factor the equation if possible or use the quadratic formula.
- Solve for the roots by applying the formula or factoring technique.
- Check the solutions by substituting them back into the original equation.
Example 2: Working with Rational Expressions
- Factor the numerator and denominator if applicable.
- Cancel out common factors, but make sure to check for restrictions.
- Combine any like terms and simplify the expression.
- Verify the simplified form by plugging in a sample value for the variable.
These step-by-step guides not only show the process but also emphasize the importance of checking each calculation to avoid simple mistakes. Practicing regularly with this method will boost your problem-solving skills and help you gain confidence in handling more complex challenges.
How to Solve Polynomial Equations
Solving polynomial equations requires understanding the structure of the equation and applying appropriate methods to find the roots. These equations can vary in complexity, from simple quadratics to higher-degree polynomials. The goal is to simplify the equation and solve for the variable by applying strategies like factoring, using the quadratic formula, or synthetic division. Mastering these techniques is essential for tackling a wide range of problems.
Factoring Polynomials
The first step in solving many polynomial equations is factoring the expression. For quadratics, this often involves finding two numbers that multiply to give the constant term and add to give the coefficient of the linear term. Once the polynomial is factored, you can set each factor equal to zero and solve for the variable.
Using the Quadratic Formula
If factoring is difficult or not possible, the quadratic formula is a reliable alternative for solving quadratic equations. The formula is:
x = (-b ± √(b² – 4ac)) / 2a
This formula applies to equations in the form ax² + bx + c = 0, where a, b, and c are constants. By substituting these values into the formula, you can find the solutions for the variable.
For higher-degree polynomials, methods such as synthetic division or numerical approaches may be necessary to break down the equation further and find all the roots. It’s important to keep practicing these methods to become comfortable with different types of polynomial equations and their solutions.
Tips for Mastering Rational Functions
Rational functions, which are ratios of polynomials, can be tricky to master, but with a clear understanding of their structure and behavior, you can solve them confidently. These functions often involve identifying domain restrictions, simplifying expressions, and analyzing asymptotes. By applying systematic strategies and practicing problem-solving, you can gain a solid grasp on how to work with these types of functions.
Understanding the Domain and Restrictions
One of the first steps in working with rational functions is to understand the domain. This involves identifying the values of the variable that would make the denominator equal to zero, as these values are undefined. By setting the denominator equal to zero and solving for the variable, you can determine the domain restrictions. Always remember to exclude these values when working with the function.
Identifying Vertical and Horizontal Asymptotes
Asymptotes are essential to understanding the behavior of rational functions. Vertical asymptotes occur where the denominator equals zero (but the numerator does not), and they indicate where the function tends to infinity. Horizontal asymptotes are determined by the degrees of the numerator and denominator and describe the end behavior of the function. By analyzing these asymptotes, you can predict how the function behaves at extreme values of the variable.
By familiarizing yourself with these key concepts and practicing solving rational functions, you’ll be better prepared to handle the challenges they present. The more you practice simplifying and analyzing rational expressions, the more intuitive these steps will become, leading to greater confidence and accuracy in solving related problems.
Understanding Exponent Rules in Algebra 2
Exponents are a fundamental concept in mathematics that simplify expressions and equations. By applying the correct exponent rules, you can manipulate expressions efficiently and solve problems more easily. These rules are crucial for simplifying powers, handling negative exponents, and working with fractional powers. Mastering these principles is essential for solving a wide range of problems accurately.
Key Exponent Rules
Here are the most important rules to remember when working with exponents:
- Product Rule: When multiplying two expressions with the same base, add the exponents.
Example: a^m × a^n = a^(m + n) - Quotient Rule: When dividing two expressions with the same base, subtract the exponents.
Example: a^m ÷ a^n = a^(m – n) - Power Rule: When raising a power to another power, multiply the exponents.
Example: (a^m)^n = a^(m × n) - Zero Exponent Rule: Any non-zero number raised to the power of zero equals one.
Example: a^0 = 1 (where a ≠ 0) - Negative Exponent Rule: A negative exponent indicates the reciprocal of the base raised to the positive exponent.
Example: a^(-n) = 1/a^n - Fractional Exponents: A fractional exponent indicates a root. The numerator is the power, and the denominator is the root.
Example: a^(1/n) = n√a
Applying the Rules
These rules are essential for simplifying complex expressions. Practice applying them in various scenarios, such as simplifying powers of variables or solving equations that involve exponents. By understanding and utilizing these rules, you will be able to manipulate expressions more effectively, which is crucial for solving higher-level problems and understanding advanced concepts.
Graphing Techniques for Algebra 2
Graphing is an essential skill for visualizing mathematical relationships and understanding the behavior of equations. By mastering different graphing techniques, you can more easily interpret complex functions and find solutions to various types of problems. Whether you are plotting linear equations, quadratic functions, or more advanced curves, knowing the best methods will help you analyze and solve equations more effectively.
Graphing Linear and Quadratic Functions
Graphing linear and quadratic functions is a foundational skill that lays the groundwork for more complex graphing techniques. To graph a linear equation, identify the slope and the y-intercept, and plot the line based on these values. For quadratic functions, start by finding the vertex and the axis of symmetry, then plot additional points to form the parabola. Both types of graphs provide insights into the relationship between variables and can be used to solve various problems.
Working with Higher-Degree Polynomials and Rational Functions
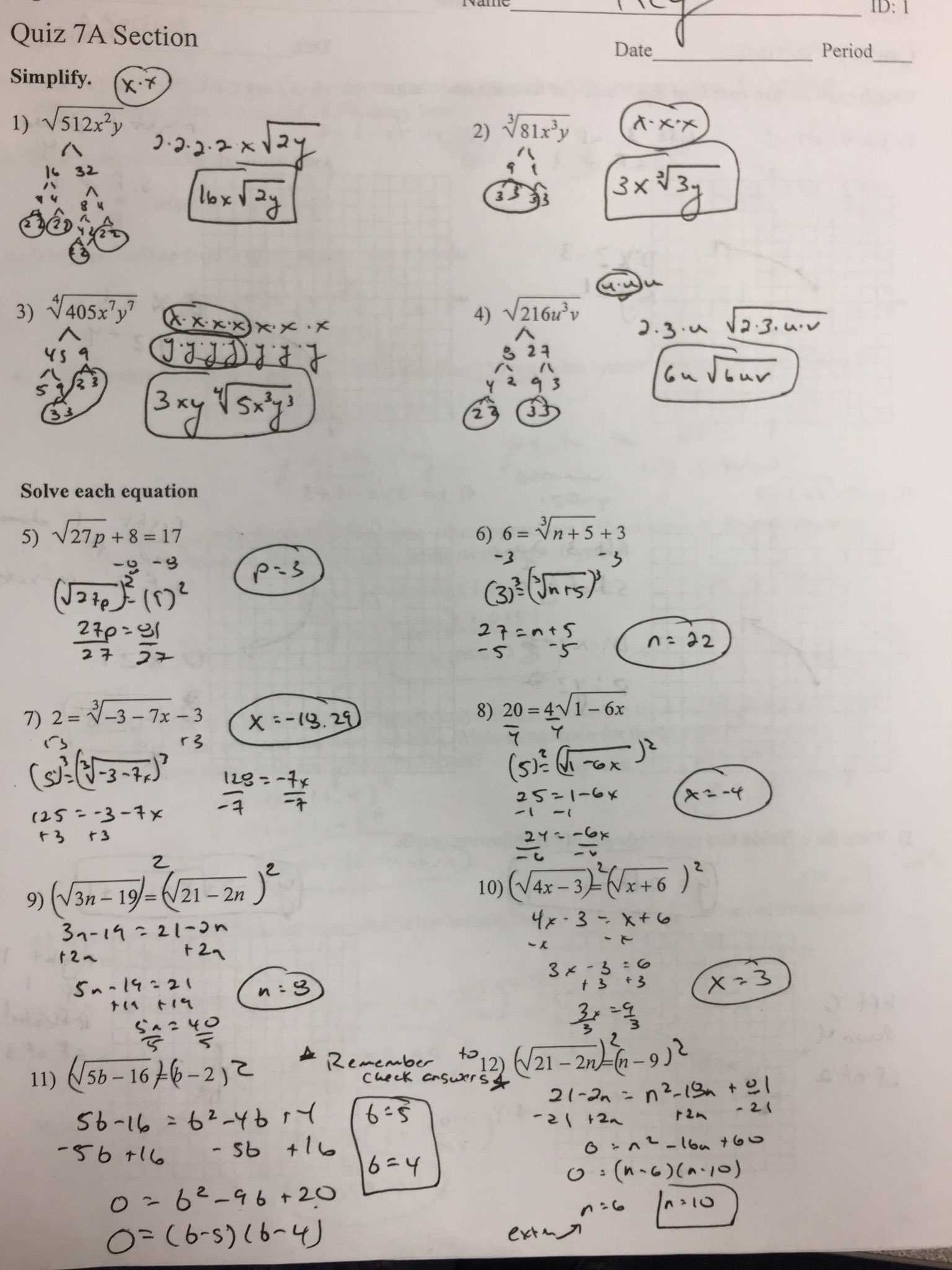
Graphing higher-degree polynomials and rational functions requires a deeper understanding of the function’s behavior. For polynomials, look for key features such as intercepts and turning points to sketch the curve. In the case of rational functions, identify vertical and horizontal asymptotes, and analyze the function’s end behavior to create an accurate graph. These techniques allow you to visualize the function’s overall shape and understand how changes in the equation affect the graph.
By practicing these graphing techniques and understanding their underlying principles, you’ll become proficient in plotting a wide range of functions, which will help in both solving equations and interpreting real-world applications of mathematical models.
Reviewing Word Problems
Word problems are a crucial part of mathematics, requiring the ability to interpret real-life scenarios and translate them into mathematical expressions. These problems test your understanding of concepts and how to apply them to solve practical challenges. By focusing on the key information and following a structured approach, you can break down complex problems and find effective solutions.
Steps to Solve Word Problems
Here are the general steps to approach and solve most word problems:
- Understand the Problem: Read through the problem carefully to determine what is being asked. Identify important values and relationships described in the text.
- Define Variables: Assign variables to the unknown quantities. These could represent numbers, time, or other measurable aspects mentioned in the problem.
- Formulate Equations: Based on the relationships and conditions in the problem, create the appropriate mathematical equations to represent the situation.
- Solve the Equations: Apply suitable methods, such as substitution or elimination, to find the values of the variables. Simplify the equations where necessary.
- Check Your Answer: Review the solution to ensure it makes sense in the context of the problem. Verify that the result is reasonable and answers the question correctly.
Types of Word Problems
There are several types of word problems you may encounter, including:
- Rate and Time Problems: These problems involve calculating speed, distance, and time, using formulas like distance = rate × time.
- Work Problems: Problems that describe tasks completed by multiple workers or machines, often involving combined rates of work.
- Mixture Problems: These problems require finding the final concentration or composition when different substances are mixed together.
- Profit and Cost Problems: These typically involve determining profit or cost by considering factors such as price and quantity.
- Number Problems: These problems involve relationships between different numbers, such as finding an unknown number based on its relationship to others.
By practicing different types of word problems and consistently applying the outlined steps, you can strengthen your problem-solving skills and improve your ability to tackle complex scenarios. The more you practice, the more efficient and confident you will become in solving word problems.
Preparing for Trigonometry on the Midterm

Trigonometry plays a significant role in many mathematical assessments, and mastering its core concepts is crucial for performing well. This area focuses on the relationships between angles and sides in triangles, along with the application of trigonometric functions such as sine, cosine, and tangent. Understanding these functions and their properties will help you approach problems more confidently. The key to success is consistent practice and familiarity with common formulas and identities.
Here are some essential steps to guide your preparation:
| Preparation Tip | Description |
|---|---|
| Understand Key Functions | Review and memorize the definitions of sine, cosine, and tangent, and how they relate to a right triangle. Focus on their unit circle representations. |
| Master Trigonometric Identities | Become familiar with fundamental identities such as the Pythagorean identity and angle sum/difference formulas. These identities are essential for simplifying and solving problems. |
| Practice Word Problems | Work on problems that involve real-world applications of trigonometry, such as calculating distances and angles in navigation and physics problems. |
| Focus on Graphing | Learn to graph trigonometric functions like sine, cosine, and tangent. Pay attention to their amplitude, period, and phase shifts. |
| Work on Inverse Functions | Review how to solve equations involving inverse trigonometric functions, as these often appear in higher-level questions. |
By concentrating on these areas and solving various practice problems, you will strengthen your ability to tackle trigonometric questions effectively. The more you familiarize yourself with the material and apply the concepts, the more confident you’ll be when it comes time to solve related problems on the test.
Important Formulas to Remember

Having a solid grasp of key formulas is essential for solving a variety of problems efficiently. These mathematical relationships form the foundation for a wide range of tasks, from simplifying equations to analyzing functions. By committing these formulas to memory, you’ll be well-equipped to handle different types of challenges and perform calculations more effectively.
Essential Arithmetic and Exponent Rules
Knowing the fundamental rules of arithmetic and exponents is crucial for simplifying expressions and solving complex problems. These principles are often the building blocks of more advanced topics:
- Distributive Property: a(b + c) = ab + ac
- Product of Powers: a^m * a^n = a^(m + n)
- Quotient of Powers: a^m / a^n = a^(m – n)
- Power of a Power: (a^m)^n = a^(m * n)
Key Formulas for Quadratics
Quadratic functions are central to solving many problems, and knowing how to manipulate them is vital. Here are the key formulas to remember when working with quadratics:
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a
- Factoring Form: ax² + bx + c = (x + p)(x + q)
- Vertex Form: y = a(x – h)² + k
By practicing these formulas and understanding their applications, you’ll be able to simplify problems, find solutions more efficiently, and gain confidence in your problem-solving skills. Mastery of these key formulas provides a strong foundation for more advanced concepts and real-world applications.
Time Management During the Exam
Effectively managing your time during a test is essential to ensure that you can address all questions thoroughly. Prioritizing tasks, pacing yourself, and allocating enough time for each section are all critical strategies for success. By adopting a systematic approach, you can reduce stress and increase the likelihood of completing the assessment within the allotted time frame.
Start by quickly skimming through the entire set of questions before diving into any one section. This will help you gauge the difficulty level of each question and decide which ones to tackle first. Consider starting with the problems you find easiest, as they will build your confidence and give you more time for the more challenging ones.
As you move through the questions, keep an eye on the clock. Set time limits for each section to prevent spending too long on any one problem. If a question seems overly time-consuming, move on and come back to it later if needed. Ensure that you leave enough time at the end to review your answers and make necessary corrections.
By practicing effective time management, you will be able to complete the assessment efficiently and accurately, ensuring that you maximize your performance and minimize the chances of missing important questions.
How to Stay Calm During the Test
Maintaining composure during a timed assessment is crucial for optimal performance. When faced with pressure, it is easy to become anxious or overwhelmed. However, by adopting a few simple techniques, you can stay focused, manage stress, and approach each problem methodically.
Take Deep Breaths: If you feel tension building, pause for a moment and take a few deep, calming breaths. This helps to reduce anxiety, improve focus, and reset your mind. Even a brief pause can clear mental fog and bring clarity to your thinking.
Stay Positive: Keep a positive mindset throughout the process. Remind yourself that you have prepared well and that you are capable of handling the challenges ahead. Negative thoughts can create unnecessary stress, so instead, focus on your strengths and tackle each question one at a time.
Break the Test Into Smaller Tasks: Instead of viewing the entire assessment as one overwhelming challenge, break it down into smaller, more manageable tasks. Focus on completing one question at a time, and resist the urge to worry about the others until you’ve finished what’s in front of you.
Remember: Staying calm is not about avoiding stress entirely but about managing it effectively. With these strategies, you will maintain the clarity and focus needed to perform at your best, no matter the circumstances.