Algebra 1 Test 1 Answers Explained and Solved

Mastering the foundational principles of mathematics is essential for success in more advanced topics. The initial assessment in this subject serves as an opportunity to test your understanding and problem-solving abilities. Whether you’re preparing for a class evaluation or simply looking to reinforce your knowledge, it’s important to approach these exercises with clarity and confidence.

By breaking down each problem, you can uncover the steps needed to find the correct results. Developing a strong grasp of basic techniques will help you tackle similar challenges more efficiently in the future. Emphasizing critical thinking and pattern recognition plays a key role in finding solutions and improving your skills.

Through focused practice and review, you can enhance your ability to solve problems quickly and accurately. Applying logical methods and refining your approach will help you achieve better results and build a strong mathematical foundation for future success.

Algebra 1 Test 1 Answers Overview

In any subject, an initial assessment is crucial for evaluating how well you’ve grasped the key concepts. This section highlights the importance of reviewing solutions and understanding the logic behind each problem. By thoroughly examining each solution, you’ll gain insight into the underlying principles and refine your approach for future challenges.

Approaching the Problems

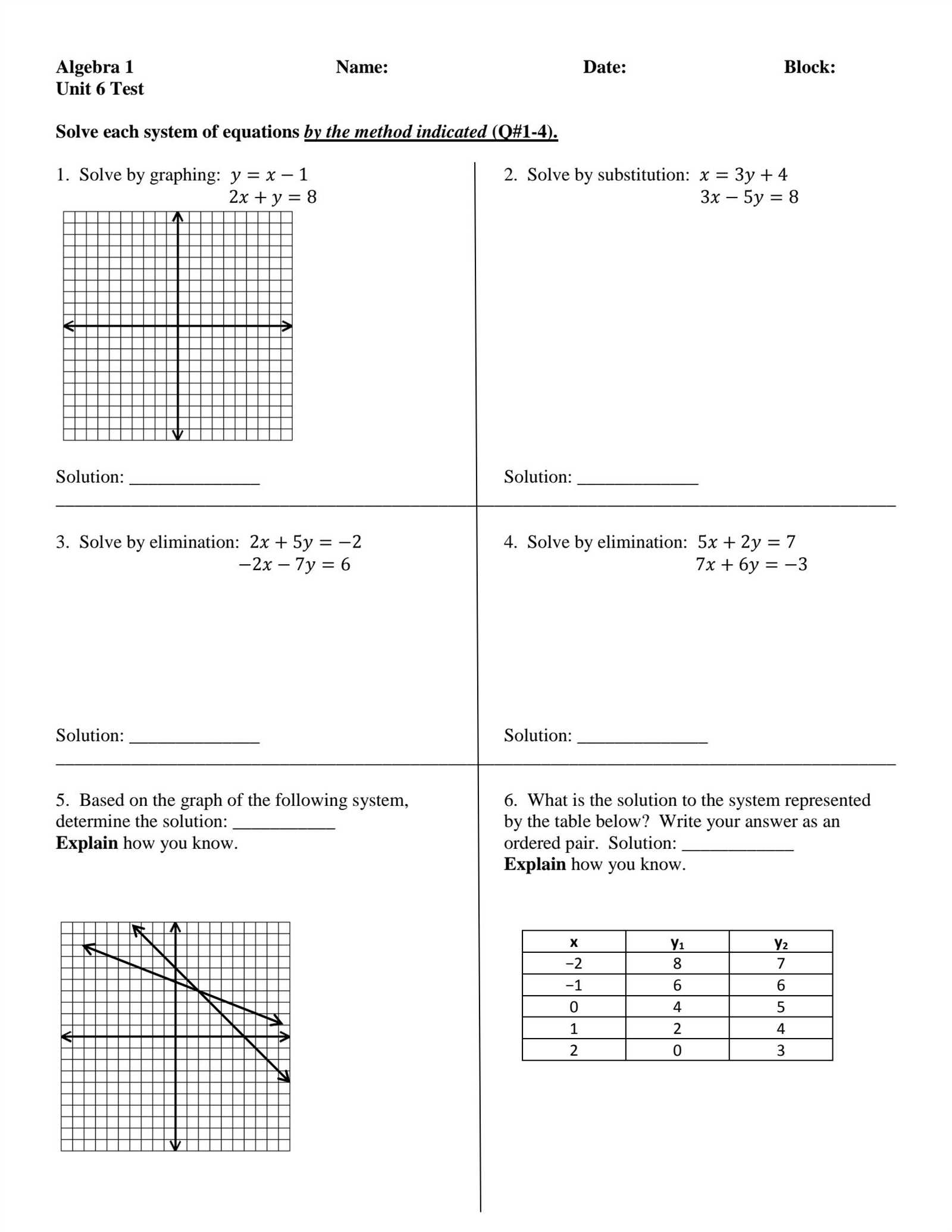
When working through each problem, it’s essential to focus on the methodology. Breaking down the steps and identifying patterns will allow you to recognize how similar challenges are structured. With a clear strategy, tackling complex equations becomes more manageable.

Common Pitfalls to Avoid

Many students encounter recurring mistakes when dealing with certain problem types. These errors often stem from misinterpreting questions or overlooking simple steps in the solution process. By reviewing common missteps and learning to avoid them, you can improve both accuracy and efficiency.

Understanding Key Algebra Concepts

Grasping the core principles of this subject is essential for tackling various types of problems effectively. The foundation consists of concepts that are used to solve equations, manipulate expressions, and understand relationships between variables. Once these ideas are understood, more complex problems become simpler to approach.

Core Concepts to Master

To build a strong foundation, focus on the following key ideas:

Variables: Symbols that represent unknown values, often used in equations.
Equations: Mathematical statements that express the equality of two expressions.
Functions: Relationships between inputs and outputs where each input corresponds to exactly one output.
Exponents: Representing repeated multiplication of a number by itself.
Factoring: Breaking down an expression into simpler parts that multiply together to give the original expression.

Applying the Concepts

Once you have a grasp of these key ideas, the next step is to apply them in practical situations. Practice solving problems by using these concepts to manipulate expressions and solve for unknown values. Through consistent practice, you’ll improve your ability to work through more complex scenarios.

Start with basic equations and gradually increase difficulty.
Work through word problems to improve your ability to identify which concept to apply.
Review your solutions to understand where mistakes might have occurred and how to correct them.

How to Approach Test Problems

When faced with problems that assess your understanding, having a structured approach can significantly improve your chances of success. Instead of rushing through, take a step-by-step approach to break down the question and identify what is being asked. With the right strategy, even challenging problems become more manageable.

Steps to Tackle Problems Effectively

Follow these guidelines to ensure you are addressing each problem systematically:

Read the Problem Carefully: Understand the question and what information is given.
Identify Key Information: Highlight important details that will help you solve the problem.
Choose the Right Approach: Determine which methods or formulas will help you find a solution.
Work Through Step-by-Step: Break down the problem into smaller, manageable parts.
Double-Check Your Work: Review your solution to ensure all steps are correct and logical.

Common Pitfalls and How to Avoid Them

During problem-solving, it’s easy to make simple mistakes. Be aware of the following errors:

Skipping Steps: Skipping important intermediate steps can lead to incorrect solutions.
Overcomplicating Problems: Sometimes, problems can be solved with simpler methods than initially thought.
Misinterpreting Information: Ensure you fully understand the problem before jumping into calculations.

Step-by-Step Problem Solving

Approaching complex challenges methodically is crucial for finding accurate solutions. By breaking down each problem into manageable steps, you can ensure that all aspects are addressed carefully and logically. This approach helps to avoid errors and makes even the most difficult problems more approachable.

Breaking Down the Process

Follow these key steps to solve problems efficiently:

Understand the Question: Read the problem carefully and identify exactly what is being asked.
Gather Information: Take note of all the relevant data provided, including numbers, variables, and relationships.
Plan Your Approach: Decide on the most suitable method or formula to apply based on the information you’ve gathered.
Execute the Plan: Work through the problem, applying the chosen approach step by step.
Check Your Solution: Review each step to verify that the final answer is correct and all parts of the question were addressed.

Tips for Effective Problem Solving

Here are some additional strategies to improve your problem-solving skills:

Stay Organized: Keep your work neat and structured, so it’s easy to track your progress.
Use Simple Methods: Always opt for the simplest and most straightforward approach to avoid confusion.
Don’t Rush: Take your time to think through each step, even if the problem seems simple.
Review Common Mistakes: Reflect on past errors to avoid repeating them in future problems.

Common Mistakes in Algebra 1

When working through mathematical problems, it’s easy to overlook certain details or make small errors that can affect the entire solution. Understanding the most common pitfalls helps to avoid them and ensures more accurate results. Identifying these mistakes early on can make a significant difference in overall performance and understanding of the material.

Frequent Errors and How to Avoid Them

Here are some of the most common mistakes students make and how to prevent them:

Common Mistake	Cause	How to Avoid
Forgetting to distribute	Neglecting to apply multiplication across parentheses	Always double-check that you distribute across all terms within parentheses
Sign errors	Incorrectly handling positive and negative signs, especially when adding or subtracting	Pay close attention to signs before performing any operations
Incorrectly solving for variables	Misapplying inverse operations or skipping steps	Take time to isolate the variable step by step, checking each move carefully
Misinterpreting the problem	Overlooking what the problem is asking or misunderstanding the relationships	Read the problem thoroughly, highlighting important information before solving

Improving Accuracy

To minimize errors, practice and review are essential. Continuously solving problems while focusing on avoiding these common mistakes will help you develop better problem-solving habits. Additionally, learning from errors and understanding where things went wrong can significantly enhance your skills.

How to Interpret Word Problems

Word problems often present a scenario that requires you to translate real-life situations into mathematical terms. The challenge lies in extracting relevant information from the text and determining the appropriate approach to solve it. Developing a clear strategy for interpreting these problems is essential to finding accurate solutions.

To effectively interpret word problems, it’s crucial to identify the key components: what is being asked, the data provided, and how those elements relate to each other. A structured method can help break down the problem into smaller, more manageable steps, making it easier to apply the right mathematical operations.

Key Steps for Interpreting Word Problems:

Read Carefully: Ensure you understand every part of the problem before attempting to solve it.
Identify Important Information: Highlight or underline numbers, relationships, and conditions that are relevant to the solution.
Translate Words into Numbers: Convert phrases like “total,” “difference,” or “per” into mathematical expressions.
Plan Your Solution: Decide what type of calculation or operation is needed to solve the problem.
Double-Check Your Interpretation: Before solving, make sure you haven’t missed any crucial details.

By practicing these steps, you’ll improve your ability to read and interpret word problems with greater accuracy and confidence, ultimately leading to more effective problem-solving skills.

Practice Problems for Algebra Mastery

Mastering any subject requires consistent practice, especially when it comes to solving equations and manipulating expressions. Regularly working through problems helps reinforce key concepts and improves problem-solving speed. The more practice you get, the more confident you’ll become in applying different techniques to a variety of challenges.

Here are some practice problems designed to strengthen your skills:

Problem	Type	Solution
2x + 3 = 11	Linear Equation	x = 4
3(2y – 4) = 12	Linear Equation with Parentheses	y = 4
x² – 5x + 6 = 0	Quadratic Equation	x = 2 or x = 3
5x + 3 = 2x + 15	Simple Equation	x = 4
4a – 7 = 3a + 2	Linear Equation	a = 9

Working through these problems will enhance your ability to handle various types of equations and refine your approach to problem-solving. Be sure to check your solutions and analyze each step to fully understand the reasoning behind the answers.

Effective Test-Taking Strategies

Approaching an assessment requires more than just knowledge of the material; it demands careful preparation, time management, and a strategic approach to maximize your performance. By implementing certain techniques during the exam, you can improve your efficiency and reduce stress, ensuring that you tackle each problem with confidence.

Key Strategies for Success

Here are some proven strategies to help you perform at your best:

Read Instructions Carefully: Before jumping into solving problems, ensure you fully understand the instructions for each section or question.
Manage Your Time: Allocate a specific amount of time for each question. Don’t linger too long on one problem if you’re unsure of the answer; move on and return to it later.
Start with What You Know: Begin with the questions you find easiest. This will help build confidence and ensure you secure quick points early on.
Work Neatly and Organize Your Work: Keep your work clean and well-organized so that it’s easy to follow your steps, especially when reviewing later.
Double-Check Your Work: If time permits, review your answers and check for any possible mistakes or overlooked details.
Stay Calm: Don’t let stress overwhelm you. Stay focused, take deep breaths, and work through problems methodically.

Additional Tips for Performance

In addition to these strategies, consider the following tips to further enhance your performance:

Stay Positive: A positive mindset can help you stay calm and confident during the exam.
Practice Under Timed Conditions: Simulate real exam conditions by practicing problems with a timer to build comfort and speed.
Learn from Past Mistakes: After taking practice tests or reviewing your past exams, analyze your mistakes and focus on improving those areas.

Tips for Improving Algebra Skills

Improving your problem-solving abilities takes consistent effort and practice. To master the concepts and techniques required for solving equations and manipulating expressions, it’s essential to focus on key strategies that build both understanding and speed. By implementing these tips, you can significantly enhance your skills and tackle more complex problems with confidence.

Here are several effective ways to strengthen your problem-solving abilities:

Tip	Description	Benefit
Practice Regularly	Work through a variety of problems to reinforce different concepts and techniques.	Increases familiarity with different problem types and solidifies your understanding.
Focus on Fundamentals	Master the basic rules and operations, such as solving for variables and simplifying expressions.	Helps build a strong foundation for tackling more advanced problems later.
Learn from Mistakes	After solving a problem, review your work to understand any errors and correct them.	Improves accuracy by identifying common mistakes and preventing them in the future.
Use Online Resources	Access videos, tutorials, and practice worksheets to explore different approaches to solving problems.	Provides alternative explanations and insights, making it easier to grasp difficult concepts.
Ask for Help	If you’re stuck on a concept, don’t hesitate to seek assistance from a tutor or a peer.	Clarifies doubts and strengthens understanding by learning from others.

By following these strategies and remaining consistent in your practice, you’ll steadily improve your ability to solve complex problems and gain greater confidence in applying the skills you’ve learned.

Identifying Patterns in Algebra Equations

Recognizing patterns is a key skill in solving mathematical problems. By understanding how variables and constants behave in different equations, you can often find shortcuts that lead to quicker solutions. Identifying these recurring patterns not only saves time but also helps build a deeper understanding of how to manipulate expressions and solve for unknowns.

Common Patterns to Look For

Here are a few common patterns that frequently appear in equations:

Linear Relationships: When the equation involves variables raised to the first power, you can often recognize it as a linear relationship, where changes in one variable result in proportional changes in the other.
Quadratic Forms: Equations involving squared terms (such as x²) often follow a predictable pattern, leading to a factorable form or a use of the quadratic formula.
Exponential Growth or Decay: Patterns where the variable is raised to an exponent often indicate exponential growth or decay, commonly seen in problems involving rates of change.

How to Spot Patterns Effectively

Recognizing these patterns involves practice and familiarity with different equation types. Here are some tips to improve your ability to spot them:

Work on Similar Problems: Repeated practice with similar problems can help you spot common trends in the equations.
Break Down Complex Equations: When faced with a complicated problem, break it down into smaller parts to identify individual patterns that might be hiding within the equation.
Look for Common Terms: Pay attention to terms that repeat, like constants or coefficients, as they can often signal a pattern or a way to simplify the equation.

By improving your ability to identify these patterns, you’ll enhance your efficiency and accuracy when solving problems. Recognizing these trends helps you solve equations more systematically and confidently.

Solving Linear Equations with Ease

Solving linear equations is a fundamental skill that forms the backbone of many mathematical concepts. These types of equations involve finding the value of a variable that satisfies a given relationship between two expressions. By following a few simple steps, you can efficiently solve these equations and handle more complex problems with ease.

Key Steps to Solve Linear Equations

To solve linear equations, follow these basic steps:

Isolate the Variable: Start by moving all terms involving the variable to one side of the equation and all constant terms to the other side.
Simplify Both Sides: Combine like terms on both sides of the equation to make it easier to work with.
Perform Inverse Operations: Use inverse operations, such as addition, subtraction, multiplication, or division, to isolate the variable on one side of the equation.
Check Your Solution: After solving for the variable, substitute the value back into the original equation to verify that it satisfies both sides.

Example: Solving a Simple Equation

Let’s take an example to illustrate the process:

Equation: 3x + 5 = 14

Step 1: Subtract 5 from both sides:

3x = 9

Step 2: Divide both sides by 3:

x = 3

Step 3: Check the solution by substituting x = 3 into the original equation:

3(3) + 5 = 14 → 9 + 5 = 14

Since both sides are equal, the solution is correct.

By following these steps, solving linear equations becomes straightforward and can be applied to a wide range of problems, from simple to more complex scenarios.

Graphing Techniques for Algebra 1

Graphing is an essential skill in mathematics, helping to visually represent relationships between variables. By plotting points on a coordinate plane and connecting them, you can gain insights into the behavior of equations. This section explores effective methods for graphing linear equations and understanding their graphical representations.

One of the key techniques for graphing is identifying the slope and y-intercept of an equation. The slope determines the angle at which a line rises or falls, while the y-intercept tells you where the line crosses the vertical axis. These two components are often all that’s needed to plot a line on a graph.

Another method involves using a table of values. By substituting different values for the variable, you can generate corresponding points that can then be plotted. Once you have a sufficient number of points, you can connect them to form the graph of the equation.

Practice with these techniques can help you quickly and accurately graph equations, allowing you to visually interpret their solutions and better understand their behavior.

Factoring Made Simple

Factoring is a powerful technique in mathematics that involves breaking down expressions into simpler components. It allows you to rewrite complex problems in a form that is easier to solve or analyze. Understanding the basics of factoring is essential for solving a wide variety of equations and inequalities.

Identifying Common Factors

The first step in factoring is identifying common factors in the terms of an expression. For example, in the expression 4x + 8, both terms share a factor of 4. By factoring out the greatest common factor (GCF), we can rewrite the expression as:

4(x + 2)

This simplifies the problem, making it easier to work with. Always look for the GCF when factoring expressions.

Factoring Quadratic Expressions

Factoring quadratic expressions often involves finding two binomials that multiply to give the original expression. For example, to factor the expression x² + 5x + 6, we look for two numbers that multiply to 6 and add up to 5. The numbers 2 and 3 work, so the factored form is:

(x + 2)(x + 3)

With practice, recognizing patterns and factoring quadratics becomes quicker and more intuitive. Mastering this skill lays a solid foundation for solving more advanced equations and problems.

Understanding Exponents and Powers

Exponents and powers are fundamental concepts that help in simplifying expressions and solving problems more efficiently. When dealing with large numbers or repeated multiplication, exponents provide a shorthand way to express these operations. By mastering these concepts, you can handle complex calculations with ease and precision.

What Are Exponents?

An exponent represents the number of times a number (the base) is multiplied by itself. For example, in the expression 2³, 2 is the base, and 3 is the exponent. This means 2 is multiplied by itself three times, resulting in 2 × 2 × 2 = 8. Understanding how to work with exponents allows you to quickly compute large numbers and recognize patterns in mathematical expressions.

Rules for Working with Exponents

There are several important rules when working with exponents. Some of the most commonly used are:

Product of Powers: When multiplying numbers with the same base, add the exponents. Example: x² × x³ = x⁵.
Power of a Power: When raising an exponent to another exponent, multiply the exponents. Example: (x²)³ = x⁶.
Power of a Product: When raising a product to an exponent, distribute the exponent to each factor. Example: (xy)² = x²y².

These rules make it easier to simplify expressions and solve equations involving powers and exponents. With practice, you can quickly apply these concepts to more complex problems.

Solving Systems of Equations

When faced with multiple equations containing several variables, solving the system of equations allows you to find the values of those variables that satisfy all the given conditions simultaneously. This process is essential in a variety of mathematical and real-world applications, where relationships between different quantities need to be understood and solved.

Methods for Solving Systems

There are several methods used to solve systems of equations, each suited for different types of problems. These methods include substitution, elimination, and graphing. By mastering each of these techniques, you can approach problems from multiple angles and choose the best method depending on the situation.

Substitution Method

The substitution method involves solving one equation for one variable and then substituting that expression into the other equation. For example, consider the system:

2x + y = 10
x – y = 2

First, solve the second equation for x:

x = y + 2

Next, substitute this expression for x into the first equation:

2(y + 2) + y = 10

Now solve for y, and then substitute the value of y back into the expression for x to find both variables.

Elimination Method

The elimination method involves adding or subtracting the equations to eliminate one of the variables. This is typically done by manipulating the equations so that the coefficients of one variable are opposites. For example, if the system is:

3x + 4y = 12
2x – 4y = 6

By adding the two equations, the y terms cancel out:

(3x + 4y) + (2x – 4y) = 12 + 6

5x = 18

Solving for x gives:

x = 18/5

Once you have the value of one variable, substitute it back into either original equation to solve for the second variable.

Reviewing Solutions to Mathematical Problems

After completing a series of mathematical exercises, it’s important to go back and review the solutions to ensure accuracy and reinforce understanding. This review process helps identify mistakes, clarify concepts, and solidify problem-solving techniques. It also provides an opportunity to reflect on different approaches to find the correct answers and learn from any errors made along the way.

Identifying Common Errors

As you review each solution, focus on recognizing patterns of common mistakes. These errors can range from simple arithmetic slips to misinterpretations of the problem itself. Common mistakes include:

Sign errors when working with negative numbers
Incorrectly distributing terms in expressions
Forgetting to check for extraneous solutions

By pinpointing these errors, you can work towards preventing them in future problems and develop more efficient problem-solving habits.

Reinforcing Problem-Solving Techniques

Reviewing solutions not only helps you find and fix mistakes but also strengthens your understanding of the techniques involved. Whether you use substitution, elimination, or graphical methods, revisiting the steps and the logic behind each decision ensures that these methods become second nature. Consider practicing similar problems to gain more confidence in applying these strategies effectively.