
Understanding how to navigate complex mathematical concepts can be a rewarding challenge. This section provides valuable insights and techniques to strengthen your reasoning skills and enhance your confidence in tackling numerical challenges.
With a focus on practical methods, the content explores step-by-step approaches to solving intricate problems. By emphasizing logical thinking and clear strategies, it ensures a deeper comprehension of key ideas and their applications.
Whether refining basic skills or exploring advanced topics, this guide offers a balanced approach to mastering essential techniques. Learn how to avoid common pitfalls and improve efficiency in finding accurate results through consistent practice and smart strategies.
Mastering Key Concepts in Section 6
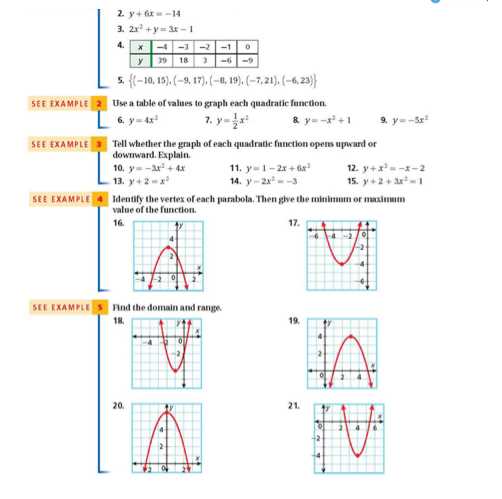
Building a strong foundation in problem-solving requires a clear understanding of core principles. This section is designed to guide you through the most important ideas, helping you develop the skills necessary to approach challenges with confidence.
By breaking down complex ideas into manageable steps, this guide ensures a comprehensive grasp of essential methods. It highlights patterns, relationships, and logical processes that form the basis for effective calculations.
Through practical examples and thoughtful explanations, you will gain the tools needed to identify effective strategies and apply them in a variety of scenarios. This approach not only simplifies the learning process but also fosters a deeper appreciation for the subject.
Understanding Algebraic Principles with Ease
Learning to navigate mathematical structures involves breaking down abstract ideas into comprehensible steps. This section provides guidance for developing logical thinking and problem-solving skills, making intricate calculations more manageable.
Core Techniques for Simplification
Identifying relationships and organizing information effectively are essential steps in mastering calculations. Simplifying problems into smaller tasks helps build confidence and ensures consistent accuracy.
Practical Strategies for Problem Solving
Applying systematic approaches to common challenges enhances understanding and speeds up the resolution process. Recognizing patterns and using efficient methods can save time and effort.
| Technique | Benefit |
|---|
| Step | Action | Objective |
|---|---|---|
| 1 | Recognize the knowns and unknowns | Identify the variables and constants that are part of the problem. |
| 2 | Simplify the expressions | Combine terms to reduce the complexity of the equation. |
| 3 | Isolate the variable | Use inverse operations to solve for the unknown value. |
| 4 | Verify the solution | Double-check that the solution satisfies the initial problem. |
Techniques for Tackling Difficult Problems
To effectively handle more complicated problems, it’s crucial to understand and apply certain strategies. Always approach the task methodically, ensuring that you take one step at a time without skipping any important details. Over time, these techniques will improve your problem-solving abilities and help you approach even the most challenging tasks with confidence.
Quick Techniques for Section 6 Success
Mastering complex concepts requires effective strategies that can simplify the process and enhance understanding. By utilizing efficient techniques, you can tackle the material with ease and achieve better results. Developing a systematic approach helps you break down challenges into manageable steps, ensuring steady progress and clearer insights.
One of the key techniques is focusing on the fundamentals. By reinforcing your understanding of basic principles, you can build a strong foundation that will support more advanced topics. Additionally, practice problems are essential for solidifying your grasp on the material. The more you practice, the more confident you become in applying concepts accurately and efficiently.
Another important technique is time management. Allocate specific time for each task, ensuring that you are not overwhelmed. By focusing on one problem at a time and giving yourself the time to work through it, you can maintain focus and improve your problem-solving speed.
Insights into Solving Quadratic Equations
Understanding how to solve equations involving variables squared is essential for mastering a wide range of mathematical problems. These equations often present themselves in various forms, each requiring a slightly different approach. Whether you’re solving for real solutions or exploring complex roots, having a structured method can make this process more manageable and intuitive.
One of the most effective strategies for solving these types of equations is factoring. By expressing the equation as the product of binomials, you can easily identify the solutions. However, not all quadratic equations are easily factorable, which is where the quadratic formula comes in handy. This method provides a universal approach to finding solutions, even when factoring is not possible.
Using the Quadratic Formula
The quadratic formula is a powerful tool that simplifies the process of solving these equations. Given a standard equation in the form ax2 + bx + c = 0, the formula is expressed as:
x = (-b ± √(b2 – 4ac)) / 2a
By plugging in the values of a, b, and c from the equation, you can quickly calculate the solutions. This method is particularly useful when the equation is difficult to factor or when you’re dealing with complex numbers.
Discriminant and Solution Types
Another important concept to understand is the discriminant, which is the expression b2 – 4ac inside the quadratic formula. The value of the discriminant determines the number and type of solutions:
- If the discriminant is positive, there are two distinct real solutions.
- If the discriminant is zero, there is exactly one real solution.
- If the discriminant is negative, the solutions are complex and not real.
By analyzing the discriminant, you can quickly determine the nature of the solutions, which is crucial for understanding the behavior of the equation.
How to Approach Word Problems Confidently
Word problems can often seem intimidating, but breaking them down step by step can help build clarity and confidence. The key is to understand what the problem is asking and to translate the words into mathematical expressions. With a solid strategy, solving these problems becomes a more manageable and even enjoyable task.
Start by carefully reading the problem to identify important information. Look for keywords and phrases that signal mathematical operations, such as “total” for addition or “difference” for subtraction. Once you have extracted the relevant details, organize them in a way that makes sense, and set up an equation or expression that represents the situation. This systematic approach is crucial for staying focused and ensuring you don’t miss important elements.
Step 1: Understand the Question
Before jumping into calculations, take the time to fully comprehend what the problem is asking. Focus on the goal of the question, whether it’s finding a specific value or determining a relationship between variables. Rewriting the problem in your own words can sometimes help solidify your understanding.
Step 2: Translate the Words into Equations
Once you have a clear idea of the question, translate the information given into mathematical terms. Identifying quantities, variables, and relationships between them is key. By expressing the problem in terms of an equation, you turn a complex situation into a solvable problem.
Practical Examples for Real-Life Applications
Understanding how mathematical concepts are used in everyday situations can enhance both your problem-solving skills and your appreciation for their real-world value. By applying mathematical thinking to daily challenges, you can gain a deeper understanding of how these techniques work beyond textbooks. Below are a few examples where these concepts play a key role in real-life scenarios.
Budgeting and Financial Planning
One of the most common real-life applications involves managing personal finances. Here’s how mathematical reasoning can help:
- Creating a monthly budget: Adding up monthly expenses and ensuring they do not exceed income.
- Understanding loans: Calculating interest and total payments over time using simple or compound interest formulas.
- Investments: Estimating returns based on various interest rates or growth projections.
Shopping and Discounts
When making purchases, it’s easy to apply mathematical principles to save money:
- Comparing prices: Determining which store offers the best deal by calculating the price per unit (e.g., cost per ounce, per liter).
- Understanding discounts: Calculating the sale price after applying a percentage discount.
- Tax calculations: Estimating the final price of an item after adding sales tax.
Travel and Time Management
Planning a trip or managing daily activities involves precise calculations, such as:
- Determining travel time: Using speed, distance, and time equations to estimate the arrival time.
- Scheduling tasks: Allocating time slots for different activities based on their duration and priority.
- Fuel efficiency: Calculating fuel consumption and costs for long-distance travel.
Key Mistakes to Avoid in Section 6
When tackling complex mathematical problems, it’s essential to avoid certain pitfalls that can hinder your progress and lead to incorrect solutions. By recognizing common errors early on, you can focus your efforts more effectively and improve your problem-solving skills. Below are some of the key mistakes to watch out for and how to avoid them.
1. Misinterpreting the Problem
One of the most frequent mistakes is misunderstanding the problem itself. It’s crucial to read each question carefully and identify what is being asked. Often, problems contain crucial details that can change the entire approach to solving it. Always take a moment to clarify the problem’s requirements before jumping to calculations.
2. Forgetting to Check for Simplifications
In many cases, problems can be simplified before solving. Forgetting to simplify expressions or equations can result in unnecessary complexity and errors in the final answer. Always look for opportunities to factor, reduce, or combine terms where possible to make the problem easier to handle.
3. Skipping Steps in Problem Solving
It can be tempting to skip steps in order to save time, especially when you feel confident. However, skipping steps often leads to mistakes and can cause you to overlook important aspects of the problem. Take the time to work through each step methodically to ensure you don’t miss any crucial details.
4. Incorrect Use of Formulas
Using the wrong formula or misapplying it is a common mistake. Always double-check the formulas you’re using to ensure they’re appropriate for the problem at hand. Moreover, pay attention to any constants or variables that may need to be adjusted based on the context.
5. Rushing Through the Process
Rushing can lead to careless mistakes such as miscalculating, missing signs, or misplacing terms. Take your time to ensure you follow each step carefully and review your work before finalizing your answer. A few extra minutes spent reviewing your solution can save you from costly errors.
Interactive Methods to Study Mathematical Concepts
Learning mathematical concepts becomes more engaging and effective when you use interactive tools and strategies. These methods allow for a deeper understanding of complex ideas while making the learning process enjoyable. By actively participating in problem-solving, you can build stronger connections to the material and improve retention.
1. Online Practice Platforms
Interactive websites and apps offer a wide range of problems that cater to various difficulty levels. These platforms provide instant feedback, allowing students to learn from their mistakes. Using these tools regularly helps reinforce concepts and builds confidence in tackling new challenges.
2. Virtual Simulations
Virtual simulations let students explore mathematical models in a dynamic environment. These simulations can visualize abstract concepts like graphing equations or transformations, making them easier to understand. By manipulating variables and observing outcomes, learners can grasp key principles more intuitively.
3. Collaborative Problem-Solving
Working together with peers in group settings encourages discussion and idea-sharing. Collaborative learning allows students to approach problems from different perspectives, enhancing their problem-solving skills. By explaining concepts to others, learners reinforce their own understanding and fill gaps in their knowledge.
4. Interactive Quizzes and Games
Quizzes and educational games create a fun and competitive atmosphere for learning. These activities challenge students to solve problems quickly and accurately while tracking their progress. By setting goals and competing with themselves, learners stay motivated to improve.
5. Digital Whiteboards and Tools
Digital whiteboards and graphing tools enable students to work out problems visually. They can draw graphs, annotate equations, and manipulate figures directly on the screen. This interactive approach makes abstract ideas more tangible and allows learners to practice in a hands-on manner.
Benefits of Revising Thoroughly
Reviewing key concepts and material thoroughly offers numerous advantages, particularly when tackling challenging topics. A well-structured revision plan helps solidify understanding, enhances retention, and prepares you for more complex problems. Taking the time to revisit and reinforce material ensures that you build a strong foundation for future learning.
- Improved Retention: Regular review helps reinforce memory and makes information easier to recall during assessments or real-life applications.
- Enhanced Understanding: Revisiting difficult concepts allows you to approach them from different angles, leading to a deeper comprehension.
- Boosted Confidence: Mastering previously challenging topics provides a sense of accomplishment, making you feel more confident in your abilities.
- Stronger Problem-Solving Skills: The more you practice, the more adept you become at applying concepts to various situations, which enhances your critical thinking abilities.
- Identification of Gaps in Knowledge: Thorough revision reveals any weak areas or misunderstandings, allowing you to address them before they become bigger obstacles.
By dedicating time to revising consistently and actively engaging with the material, you ensure that you’re better prepared for future challenges, both academically and practically.
Analyzing and Simplifying Mathematical Expressions

Breaking down and simplifying complex mathematical statements is an essential skill in understanding and solving problems effectively. The process involves recognizing patterns, grouping similar terms, and applying various techniques to make the expression more manageable. By simplifying expressions, we make calculations easier and more efficient, leading to quicker solutions and a better grasp of the overall problem.
Key Techniques for Simplifying Expressions
| Technique | Description |
|---|---|
| Combining Like Terms | Group terms with the same variable and exponent together to reduce complexity. |
| Distributive Property | Distribute multiplication over addition or subtraction to simplify expressions. |
| Factoring | Express an expression as the product of its factors to make it easier to evaluate. |
| Using Parentheses | Apply parentheses to structure expressions more clearly and prioritize operations. |
By mastering these techniques, you can confidently approach and simplify even the most intricate expressions, making problem-solving more intuitive and less time-consuming.
How to Use Online Resources Effectively
Leveraging the power of the internet can significantly enhance your learning experience. With numerous tools available, it’s important to know how to navigate and utilize them efficiently. Online resources can provide valuable insights, practice opportunities, and explanations, but it’s essential to use them purposefully to ensure they support your learning goals effectively.
Choosing the Right Platforms
Not all online resources are created equal. To maximize your learning, it’s crucial to select platforms that offer clear explanations, interactive practice, and structured content. Look for resources that cater to your learning style, whether it’s videos, tutorials, or forums for discussion.
Staying Organized and Focused
When using online resources, it’s easy to get distracted by the vast amount of information available. To stay on track, set specific goals for each session, and limit your time on each task. Organize your study materials, track your progress, and revisit challenging topics periodically to reinforce your understanding.
