
Understanding how to approach mathematical challenges involving two variables is a critical skill. This method allows us to find precise values that satisfy multiple conditions at once. It combines logical reasoning with algebraic tools to make complex problems manageable.
One effective approach is replacing one variable with an equivalent expression. This technique simplifies the original problem into a single-variable equation, making it easier to work through calculations. By mastering this, students can handle tasks involving relationships between variables with greater confidence.
This section provides insights into the method, including step-by-step explanations, practical examples, and strategies to ensure accuracy. Whether tackling practice problems or real-world scenarios, these concepts are essential for building a solid foundation in mathematical reasoning.
Understanding Systems of Equations

In algebra, solving multiple equations simultaneously allows us to determine unknown values that satisfy more than one condition. This process involves identifying the relationship between different variables and finding their precise values based on these connections.
Equations that involve more than one variable are often presented in pairs or groups, and solving them involves finding common solutions that work for all equations in the set. These relationships can represent real-life situations, such as calculating prices, quantities, or other variables that depend on each other.
There are several methods to approach these problems, each providing a different strategy for finding the values of the unknowns:
- Graphical Method: Plotting the equations on a graph to visually find the point of intersection.
- Elimination Method: Removing one variable by adding or subtracting equations.
- Substitution Method: Replacing one variable with an equivalent expression from another equation.
Each of these approaches has its strengths, depending on the complexity and nature of the equations. Mastering these techniques is essential for solving problems accurately and efficiently, whether in academic settings or practical applications.
In the next sections, we will delve deeper into these methods, focusing on one that simplifies the process and provides clear, step-by-step solutions.
What Is Substitution in Math
In mathematics, one technique involves replacing a variable in an equation with an expression from another equation. This method is designed to simplify complex problems by reducing the number of variables in a given equation, making it easier to find solutions. It is particularly useful when dealing with multiple equations that share common variables.
Instead of solving each equation independently, this approach allows us to focus on one variable at a time, creating a simpler form of the problem. The goal is to isolate a variable and substitute it into another equation to determine the unknown values more efficiently.
How It Works

The process begins by solving one equation for one variable in terms of the other(s). Then, the resulting expression is substituted into the other equation(s). This transformation reduces the system to a simpler form, often a single equation with one unknown, which can be easily solved.
Benefits of This Approach
One of the main advantages of this method is its ability to handle more complex relationships between variables. It provides a clear path to the solution and is especially useful when one equation is easily solvable for one of the variables. Additionally, it can be applied to both linear and nonlinear problems, making it a versatile tool for various mathematical challenges.
When to Use Substitution Method

This technique is particularly useful when one equation can be easily solved for one of the variables in terms of the other. By isolating a variable, it allows us to substitute its expression into the other equation, simplifying the process and reducing the number of variables to solve. This method works best in situations where the equations are not overly complex or when a variable is already in a form that can be easily replaced.
Here are some cases where this method is most effective:
- One Equation Is Simple to Solve: If one equation can easily be manipulated to isolate a variable, substitution offers a fast and straightforward path to the solution.
- Linear Equations with Clear Variables: When working with linear equations where each equation involves one variable raised to the first power, substitution is ideal for eliminating one variable at a time.
- When Other Methods Are Less Efficient: If other techniques, such as elimination, seem more time-consuming or complicated, substitution can often be a more efficient choice.
- Real-World Problems with Clear Relationships: In applied problems where variables are clearly related, this method simplifies finding the solution by expressing one variable in terms of another.
While this approach can be powerful, it is not always the most efficient for every situation. If equations are too complex or involve multiple variables, other methods might be more appropriate. However, when the conditions are right, it is a valuable tool for solving equations quickly and accurately.
Steps to Solve Using Substitution
One efficient way to handle equations with multiple variables is to replace one variable with an equivalent expression. This process transforms the original set of equations into a simpler form, allowing you to focus on finding the values of unknowns step by step. By following a structured approach, you can navigate through even complex problems with confidence.
Step-by-Step Process
The method involves a few clear stages to reach the solution:
- Isolate a Variable: Choose one equation and rearrange it to express one variable in terms of the other(s). This creates a formula that can be substituted into the remaining equation(s).
- Replace in the Other Equation: Substitute the expression found in the first step into the second equation. This will eliminate one variable, leaving a single-variable equation to solve.
- Solve the Simplified Equation: Solve the resulting equation to find the value of the remaining variable. This step typically involves basic arithmetic or algebraic operations.
- Find the Second Variable: Use the value found in the previous step and substitute it back into the expression from the fi
Common Mistakes in Substitution
While using a method to replace one variable with an equivalent expression can be a powerful tool for solving equations, it’s easy to make errors along the way. These mistakes can lead to incorrect results, making it crucial to understand the common pitfalls and how to avoid them. By being aware of these mistakes, you can improve your accuracy and streamline the problem-solving process.
1. Incorrectly Isolating a Variable
A frequent mistake occurs when rearranging an equation to isolate one variable. Failing to correctly move terms to the other side of the equation or misapplying basic algebraic rules, such as sign changes, can lead to a wrong expression. Always double-check the steps when manipulating equations to ensure the variable is isolated correctly.
2. Forgetting to Substitute the Entire Expression
Another common error is forgetting to substitute the full expression for the isolated variable into the other equation. If only part of the expression is used or the wrong terms are replaced, it can completely alter the solution. Take care to ensure that every term in the equation is replaced properly and that the entire expression is used in place of the variable.
Additional mistakes include miscalculating the values during arithmetic steps or neglecting to verify the final solution by plugging the values back into the original equations. By staying cautious and methodical, you can minimize these errors and ensure a correct result.
Benefits of the Substitution Method
Using this approach to solve problems with multiple variables offers several advantages that make it an efficient and straightforward technique. By focusing on one variable at a time, it simplifies complex relationships, making it easier to understand and solve equations. This method is particularly beneficial in cases where one equation is easy to manipulate and isolate a variable.
One of the primary benefits is the ability to reduce the problem to a single-variable equation, which can be solved using basic arithmetic or algebraic methods. This simplification helps prevent confusion, especially when working with larger systems of equations.
Key Advantages Include:
- Clarity: The process of isolating a variable and substituting it into another equation makes the problem clearer and easier to follow.
- Versatility: This method can be applied to both linear and nonlinear equations, making it useful across a wide range of mathematical problems.
- Efficiency: It often leads to quicker solutions when one equation is already simple to rearrange.
- Visual Understanding: By reducing the problem to simpler equations, it offers a better understanding of the relationship between variables and their values.
In addition, it works well in real-life applications where variables are related to one another in a direct, understandable way. Whether dealing with word problems or scientific equations, this technique is a powerful tool in problem-solving.
Real-Life Applications of Systems
Equations involving multiple variables are not just abstract concepts; they have practical applications in various fields. These types of problems frequently appear in real-world scenarios where multiple factors or conditions are interrelated. By applying mathematical techniques, we can model and solve situations that require balancing different variables simultaneously.
Business and Economics
In business and economics, managing supply and demand, pricing strategies, and budget allocations often involves working with multiple interdependent variables. For example, a company may need to find the optimal production level for two products based on their costs and expected sales. Solving this type of problem requires using relationships between variables to maximize profit or minimize cost.
Engineering and Science
In engineering, scientists and engineers routinely solve problems involving multiple variables. For instance, in structural engineering, determining the forces acting on different parts of a bridge requires understanding how various factors like weight, material strength, and environmental conditions interact. Similarly, in physics, equations for motion or energy often involve solving for multiple unknowns under specific constraints.
By using these methods to solve real-world problems, professionals in many fields are able to make data-driven decisions, optimize processes, and develop effective solutions to complex challenges.
How to Simplify Complex Systems
When faced with complex equations involving multiple variables, the key to simplifying them lies in breaking down the problem into manageable steps. Whether the equations are linear or nonlinear, the goal is to reduce the number of variables at each stage, making the system easier to solve. With the right techniques, even the most intricate relationships can be simplified for a clearer solution path.
Step 1: Identify a Variable to Isolate
The first step in simplifying any set of equations is to choose a variable that can be easily isolated. Look for an equation where one variable is already expressed in terms of the others, or where isolating one variable is straightforward. Once you have this, rearrange the equation to express that variable on one side.
Step 2: Substitute and Eliminate

Once a variable is isolated, substitute its expression into the other equation(s) to eliminate one variable. This transforms the system into a single-variable equation, which is much easier to solve. By systematically eliminating variables, the equations become progressively simpler, allowing you to solve for the unknowns step by step.
Additional Tips:
- Look for Common Factors: If the coefficients or constants in the equations are large or complicated, check if there are any common factors that can be factored out first. This can make the process easier.
- Simplify Early: Don’t wait until the end to simplify; simplify as you go along to avoid unnecessary complexity.
- Check for Redundant Equations: If two equations are very similar, one might be redundant. Removing unnecessary equations can help focus on the most relevant ones.
By following these steps, complex sets of equations can be broken down into simpler parts, making the solution process faster and more efficient. With practice, you’ll develop an intuition for recognizing which variable to isolate first and how to simplify each equation along the way.
Checking Your Solution for Accuracy
After completing the process of solving an equation, it’s important to verify that the solutions are correct. This ensures that the values obtained satisfy all the given equations and constraints. Checking your solution not only confirms the correctness of your work but also helps to identify any potential errors made during the problem-solving process.
Step 1: Substitute the Solution Back
The first step in verifying your solution is to substitute the values of the variables back into the original equations. If the values satisfy all the equations, the solution is correct. If not, you may need to recheck your work or reconsider your approach.
Step 2: Check for Consistency

Ensure that the solution is consistent with all the given conditions. If the equations involve inequalities or specific restrictions, make sure the solution adheres to those as well. Additionally, for systems involving multiple equations, verify that the results align with each equation’s individual constraints.
Equation Substituted Values Result 2x + 3y = 12 x = 3, y = 2 12 = 12 (True) x – y = 1 x = 3, y = 2 3 – 2 = 1 (True) Final Tip: Always double-check the final solution by plugging it into all original equations. A small oversight during earlier steps may lead to incorrect results, but checking carefully ensures accuracy and confidence in your solution.
Why Substitution Beats Other Methods
When faced with a set of equations, there are multiple strategies to find the solution. However, one approach often stands out for its efficiency and ease of use, especially in cases where one equation can easily be manipulated to express a single variable. This method allows for a straightforward path to a solution, making it an ideal choice in many scenarios.
Clarity and Simplicity

One of the main advantages of this method is its simplicity. By isolating a variable in one equation and directly substituting it into the other, you can reduce a system of multiple variables to just one. This reduction makes it easier to focus on solving for the remaining variable, without dealing with multiple unknowns at once. The process is often quicker compared to other techniques, particularly when the equations are already set up in a way that facilitates substitution.
When Other Methods Fall Short

In contrast to methods like elimination, which may require extensive manipulation of the equations, substitution can be more efficient when one equation is easily solvable for a single variable. For example, if one of the equations already has a variable isolated, there’s no need for additional steps such as multiplying equations or combining them. Substitution cuts through this complexity and provides a quicker solution without compromising accuracy.
Fewer Errors
Additionally, this method reduces the chances of making errors. With fewer steps and less complicated manipulation, there’s less room for mistakes. The process is direct and intuitive, which helps in maintaining accuracy throughout.
In many cases, substitution is simply the most straightforward and effective approach, especially when dealing with simple to moderate equations. For these reasons, it remains one of the most preferred methods for solving multi-variable problems.
Example Problems with Substitution

To better understand the process, let’s work through a few examples where we replace one variable with an expression from another equation. This method makes it easier to isolate and solve for unknowns in a set of linear equations. By strategically expressing one variable in terms of the other, we can simplify complex problems and find solutions step by step.
Example 1:
Consider the following equations:
- 2x + 3y = 14
- x – y = 1
Step 1: Solve for x in the second equation:
x = y + 1
Step 2: Substitute the expression for x into the first equation:
2(y + 1) + 3y = 14
Step 3: Simplify and solve for y:
2y + 2 + 3y = 14
5y + 2 = 14
5y = 12
y = 12 / 5
y = 2.4
Step 4: Now substitute y = 2.4 into x = y + 1 to find x:
x = 2.4 + 1
x = 3.4
The solution is x = 3.4 and y = 2.4.
Example 2:
Practice Exercises for Substitution
To become more comfortable with the method of replacing variables, it’s important to practice with various problems. The following exercises will help you apply the techniques to find solutions step by step. Start with simpler problems and gradually move to more complex ones as you build confidence.
Exercise 1
Solve the following set of equations:
3x + 4y = 18 x – y = 2 Start by solving one equation for one variable and substitute it into the other equation to find the solution.
Exercise 2
Solve this set of equations:
2x + 5y = 23 3x – 4y = 10 Use the same approach as in Exercise 1 to isolate a variable and substitute into the second equation.
Exercise 3
Try solving these equations:
5x – 2y = 12 4x + 3y = 20 Here, consider isolating one of the variables and using it to simplify the second equation to find the solution.
After completing these exercises, double-check your work to ensure all calculations were done correctly. With more practice, this method will become an efficient and effective tool for solving such problems.
Using Substitution in Word Problems
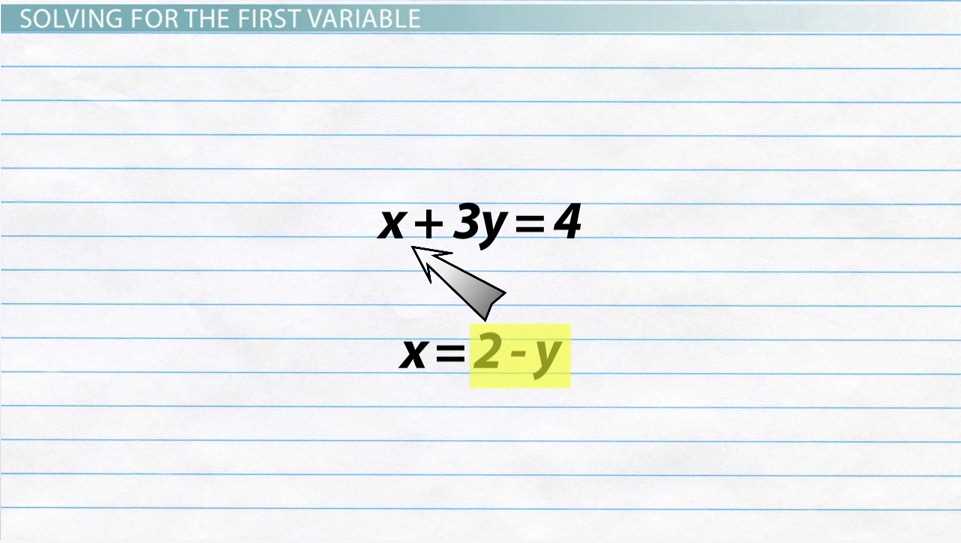
Word problems often present real-life situations that can be represented using mathematical equations. By translating the given information into equations, it becomes possible to find solutions. The process of replacing one variable with an equivalent expression helps simplify these problems and find the correct answers. Below are steps on how to approach word problems using this method:
- Read the Problem Carefully: Begin by understanding the context and identifying the variables that represent the unknown quantities.
- Set Up Equations: Translate the verbal descriptions into mathematical expressions. Each piece of information in the problem should correspond to an equation.
- Isolate a Variable: Choose one of the equations and solve for one variable in terms of the other. This will allow you to substitute into the other equation.
- Substitute and Solve: Take the expression for the isolated variable and replace it in the other equation. Then solve for the remaining variable.
- Verify the Solution: After finding the values for the variables, check if they satisfy both equations. Ensure the solution makes sense within the context of the problem.
Let’s look at an example:
Example Problem

A total of 50 people attended two different events at a community center. Tickets for the first event cost $10, and tickets for the second event cost $15. If the total amount collected from ticket sales was $650, how many tickets were sold for each event?
- Step 1: Let x represent the number of tickets sold for the first event and y represent the number of tickets sold for the second event.
- Step 2: Set up the equations based on the information given:
- x + y = 50 (the total number of tickets sold)
- 10x + 15y = 650 (the total amount collected from ticket sales)
- Step 3: Solve one equation for one variable. For example, solve x + y = 50 for x:
- x = 50 – y
- Step 4: Substitute x = 50 – y into the second equation (10x + 15y = 650) to find y:
- 10(50 – y) + 15y = 650
- 500 – 10y + 15y = 650
- 500 + 5y = 650
- 5y = 150
- y = 30
- Step 5: Substitute y = 30 into x = 50 – y to find x:
- x = 50 – 30 = 20
- Step 6: Verify the solution by checking both equations:
- Step 1: Begin by rewriting each equation in a form that is easy to graph, typically the slope-intercept form (y = mx + b).
- Step 2: Plot the graph of each equation on the coordinate plane. For linear equations, identify the y-intercept and the slope to draw the line accurately.
- Step 3: Look for the point where the lines intersect. The coordinates of this point are the values of the variables that satisfy both equations simultaneously.
- Step 4: If the lines do not intersect, the equations may not have a solution, or they may represent parallel lines with no common point. If the lines overlap completely, the equations have infinitely many solutions.
- y = 2x + 1
- y = -x + 4
Graphical Representation of Solutions
In many mathematical problems, visualizing the solutions can provide a clearer understanding of how the variables interact. A graphical approach allows you to see where different equations intersect, revealing the values that satisfy all the given conditions. This method is particularly useful when dealing with multiple variables, as it turns abstract equations into tangible visuals. The process involves plotting lines or curves on a coordinate plane and finding their points of intersection, which represent the solution to the problem.
Steps for Graphing Solutions
Example
Consider the following two equations:
To graph these equations:
- For y = 2x + 1, plot the y-intercept at (0, 1) and use the slope of 2 to find another point, such as (1, 3).
- For y = -x + 4, plot the y-intercept at (0, 4) and use the slope of -1 to find another point, such as (1, 3).
Both lines intersect at the point (1, 3). Therefore, the solution to this system of equations is x = 1 and y = 3.
Graphical methods provide a visual and intuitive way to approach problems, offering immediate insight into the relationship between the variables. Whether the solution is a single point, no solution, or infinitely many solutions, the graph makes the outcomes clear and accessible.
Key Tips for Faster Calculations
Performing quick and accurate calculations is a valuable skill, especially when dealing with complex mathematical problems. There are several strategies that can help you streamline your process, reduce errors, and save time. Whether you’re working with basic arithmetic or more advanced algebraic expressions, knowing how to approach problems efficiently can make all the difference in achieving faster results.
1. Simplify Expressions Early
One of the most effective ways to speed up calculations is to simplify the expressions as early as possible. Breaking down complex terms or factoring equations before starting with numerical calculations can significantly reduce the steps needed later on. For example:
- Factor common terms in algebraic expressions to make multiplication or division simpler.
- Combine like terms to reduce the number of operations you’ll need to perform.
- Cancel out common factors when dealing with fractions to make the math more straightforward.
2. Use Mental Math Strategies
Being able to do calculations in your head can save time and effort when dealing with simple operations. Some mental math techniques include:
- Breaking numbers into smaller parts: Instead of multiplying large numbers directly, break them into smaller, easier-to-multiply components. For instance, 14 × 6 can be simplified by first calculating (10 × 6) + (4 × 6).
- Using rounding: Round numbers to the nearest ten or hundred for quick estimation, and adjust the result accordingly.
- Memorizing multiplication tables: Quickly recall products for faster calculations when dealing with smaller numbers.
Incorporating these tips into your routine will improve not only your speed but also your accuracy in tackling mathematical challenges.
How to Handle No Solution Cases
When working with certain types of equations, you may encounter a situation where no solution exists. This often occurs when the conditions of the problem lead to an inconsistency or contradiction, meaning that no set of values can satisfy all the equations simultaneously. Understanding how to recognize and manage these cases is crucial for correctly interpreting mathematical problems and ensuring accurate results.
Recognizing Inconsistent Equations

In many cases, no solution arises from parallel lines in a graphical representation, indicating that the equations are inconsistent. This often happens when the equations represent lines with the same slope but different y-intercepts. In algebraic terms, you might encounter an equation that simplifies to something like:
2x + 3 = 2x + 5 0 = 2 Since the final statement is a contradiction, this shows there is no possible solution.
How to Handle the Situation
When you encounter no solution, it’s important to conclude that the given problem has no valid solution. Here are a few steps to guide you:
- Check for any algebraic errors in your work. Often, inconsistencies arise from simple miscalculations or oversights.
- Look for contradictory results or equations that cannot be true. This might manifest as two equal terms that are not actually equal, as seen in the example above.
- Interpret the result logically. A no-solution case means that the scenario described by the equations is not possible or feasible under the given conditions.
Once you’ve confirmed that no solution exists, it’s essential to report this conclusion clearly and accurately, avoiding further calculation attempts that might lead to confusion.
Substitution and Dependent Systems
In certain situations, mathematical equations can represent relationships where multiple equations essentially describe the same line or set of values. These relationships are referred to as dependent, meaning that one equation does not provide additional information beyond the other. Recognizing such cases is important because it highlights that an infinite number of solutions exist, as the equations are not independent but rather tied to one another.
When working with dependent cases, you may observe that after applying the method of replacing variables, the resulting equation simplifies to a true statement, such as:
x = x True for all values of x This indicates that the two equations do not represent two distinct lines but rather the same line. Thus, any solution that satisfies one equation will automatically satisfy the other, meaning there are infinitely many possible solutions.
In these scenarios, it is important to interpret the result correctly: instead of finding specific values for the variables, you recognize that the equations represent the same underlying relationship. A key takeaway is that dependent equations do not have unique solutions but rather a family of solutions that can satisfy the given conditions.
Summary: Dependent equations are linked in such a way that they represent the same line, resulting in an infinite number of solutions. Understanding this concept helps in identifying when equations are not independent and avoiding unnecessary steps in solving such cases.
Finding the Answer Key Effectively
In any mathematical task involving multiple equations, obtaining the correct result requires a systematic approach. To efficiently verify or discover solutions, it’s crucial to have a clear strategy in place. Whether you’re looking to confirm your results or check your work, a methodical approach ensures accuracy and saves time.
One of the most effective strategies is to work through each step carefully, focusing on isolating variables and simplifying the expressions as you go. When you break down the process into manageable steps, it’s easier to spot mistakes and correct them before moving on. This approach also helps in identifying patterns that may simplify the work further.
Another key aspect is to double-check the process at various stages. For example, after substituting one equation into another, you can verify that the calculations align with expectations. Additionally, when solving for the final values, always plug the solutions back into the original set of equations to ensure they satisfy all conditions.
Tips for Efficiency:
- Isolate one variable at a time.
- Use substitution progressively to reduce complexity.
- Always verify by substituting the solutions into the original equations.
- Consider using a graphical approach when applicable to visualize the relationships between equations.
By using these strategies, you’ll be able to navigate through complex problems with greater ease and confidence, ensuring that your results are both accurate and well-supported by logical steps.