
This section focuses on the essential principles and techniques that lay the groundwork for solving mathematical problems. It introduces fundamental concepts that will guide you through more complex challenges. Understanding these basics is crucial for developing a solid grasp of mathematical reasoning and problem-solving skills.
Key strategies are presented to help you understand how to approach different types of problems. You will be introduced to methods for simplifying expressions, solving equations, and analyzing relationships between quantities. These skills are applicable in various fields, from science to economics, making them vital for your academic growth.
Practice and repetition are key to mastering these concepts. The problems provided will help reinforce your understanding and develop a systematic approach to solving similar challenges in the future. With the right tools and techniques, you will be equipped to tackle more advanced topics with confidence.
CPM Algebra 1 Chapter 1 Overview
This section introduces the foundational ideas essential for building a strong mathematical framework. It covers the basic principles that underpin more complex topics, guiding you through understanding relationships between numbers and variables. By exploring these concepts, you will gain the skills needed to solve various mathematical challenges.
Core Concepts
The main focus is on understanding mathematical structures and operations. Emphasis is placed on how to manipulate and simplify expressions, as well as solve for unknowns in different types of equations. This provides a critical stepping stone for tackling higher-level problems later on.
Problem-Solving Techniques
Throughout this section, you will learn methods for approaching mathematical problems with confidence. These techniques will enable you to break down complicated expressions and equations into manageable steps, ensuring clarity and accuracy in your solutions.
| Concept | Description |
|---|---|
| Expressions | How to simplify and manipulate algebraic expressions. |
| Equations | Understanding how to solve for unknown values in equations. |
| Problem Solving | Applying strategies to solve real-world mathematical problems. |
Key Concepts in Chapter 1
This section focuses on the fundamental ideas that serve as the building blocks for more advanced mathematical reasoning. It covers essential concepts such as operations with numbers, variables, and expressions. Mastering these ideas is critical for progressing to more complex problem-solving techniques and deeper mathematical understanding.
One key concept introduced is how to identify and work with different types of expressions. You’ll learn the importance of variables and constants, and how to manipulate them in various equations. Another important focus is on the relationship between different mathematical operations and their role in simplifying and solving problems.
Additionally, this section emphasizes the significance of understanding mathematical language and notation. By grasping these key concepts early on, you’ll be able to approach more difficult topics with confidence and accuracy.
Understanding Algebraic Expressions
In this section, we focus on the structure and components of mathematical expressions. These expressions are essential for representing relationships between numbers, variables, and constants. Understanding how to identify and manipulate these elements is key to solving various mathematical problems effectively.
Mathematical expressions consist of terms that may include numbers, variables, and operators. A variable represents an unknown quantity, while constants are fixed values. The way these components interact determines the value of the expression. By mastering the manipulation of these expressions, you gain the ability to solve equations and represent real-world problems mathematically.
Operations such as addition, subtraction, multiplication, and division play a significant role in simplifying and evaluating expressions. Recognizing the patterns and relationships in these operations helps you work through more complex tasks with ease.
Simplifying Equations in Chapter 1
This section explores the process of simplifying mathematical expressions and equations to make them easier to solve. By reducing equations to their simplest form, you can efficiently find the value of unknowns and solve problems with greater ease. The goal is to break down complex problems into manageable steps.
Key Techniques for Simplification
One of the primary techniques involves combining like terms, which makes the equation simpler to work with. Additionally, understanding how to apply basic operations–such as addition, subtraction, multiplication, and division–on both sides of the equation is critical for maintaining balance and solving for the unknown.
Working with Fractions and Decimals
Equations often include fractions or decimals, which may require additional steps to simplify. By multiplying both sides by common denominators or converting fractions into decimals, you can make the process of solving equations more straightforward and reduce potential errors.
Mastering Linear Equations
This section focuses on understanding and solving linear equations, which are fundamental to solving a wide range of mathematical problems. Linear equations represent relationships between variables that create straight-line graphs. By mastering these equations, you will be able to handle more complex expressions with confidence and accuracy.
Solving for Unknowns
The process of solving linear equations involves isolating the unknown variable on one side of the equation. This is done by using inverse operations to remove terms and simplify the equation. Whether the equation involves addition, subtraction, multiplication, or division, each step helps bring you closer to the solution.
Graphing Linear Equations
Another key aspect of linear equations is their graphical representation. When plotted on a coordinate plane, linear equations form straight lines. Understanding how to translate an equation into a graph provides a visual understanding of the relationship between variables, which can be helpful in both solving and interpreting real-world problems.
Solving Word Problems with Algebra
This section introduces the technique of translating real-world situations into mathematical expressions and equations. Word problems often involve a narrative that can be broken down into steps, with the goal of finding an unknown value based on given information. Mastering this process allows you to apply mathematical concepts to practical problems effectively.
The key to solving word problems is identifying the relevant information and converting it into a solvable equation. Often, this involves recognizing patterns, setting up variables, and choosing the correct operations. By carefully analyzing the problem and organizing the information, you can approach even complex scenarios with a systematic method.
Step-by-Step Solutions for Practice Problems
This section provides detailed, step-by-step solutions for various practice problems. Breaking down each problem into smaller, manageable steps helps reinforce the understanding of key concepts and ensures that the problem is solved correctly. By following this structured approach, you’ll learn how to tackle similar challenges with confidence.
Each solution is broken down into clear, logical steps, allowing you to see the reasoning behind every operation. This method helps identify common strategies and techniques that can be applied to a wide range of problems.
Steps to Solve a Problem
- Read the problem carefully and identify what is given and what needs to be found.
- Define the variables and express the problem in equation form.
- Simplify the equation step by step using the appropriate mathematical operations.
- Check the solution to ensure it satisfies the original problem.
Example Problem Breakdown
- Start by identifying the unknown variable and what the equation represents.
- Translate the information into a solvable expression.
- Perform the necessary operations to isolate the variable.
- Verify the solution by substituting the value back into the equation.
Common Mistakes in Chapter 1
This section highlights some of the most frequent errors students make when working through the foundational concepts in mathematics. Understanding and recognizing these mistakes is essential for improving problem-solving skills and ensuring a more accurate approach to solving similar problems in the future.
Misinterpreting Equations
A common mistake is misinterpreting the structure of an equation. Many students confuse the terms on either side of the equation or incorrectly apply operations. It is crucial to carefully follow the order of operations and ensure that both sides of the equation remain balanced during the solving process.
Overlooking Units and Variables

Another frequent error is overlooking the meaning or role of variables and units. When solving word problems, it is essential to assign correct values to the variables and consider the context of the problem. Failing to do so can lead to incorrect conclusions or unrealistic solutions.
Tips for Success in Mathematics
Achieving success in mathematics requires a combination of understanding core concepts, practicing consistently, and applying effective strategies. By developing a strong foundation and adopting the right approach, you can improve your problem-solving skills and gain confidence in tackling complex problems.
One key to success is staying organized and focused. Break down problems into manageable steps and approach each one systematically. Additionally, practice regularly to reinforce your understanding and identify areas where you may need further clarification or improvement.
| Tip | Description |
|---|---|
| Understand the Basics | Master fundamental concepts before moving to advanced topics. |
| Practice Consistently | Repetition helps solidify your understanding and increase speed in solving problems. |
| Ask for Help | If you encounter difficulties, don’t hesitate to seek guidance from teachers or peers. |
| Stay Organized | Keep your work neat and structured to avoid mistakes and confusion. |
| Review Mistakes | Learn from errors and review problems to understand where you went wrong. |
Graphing Linear Functions
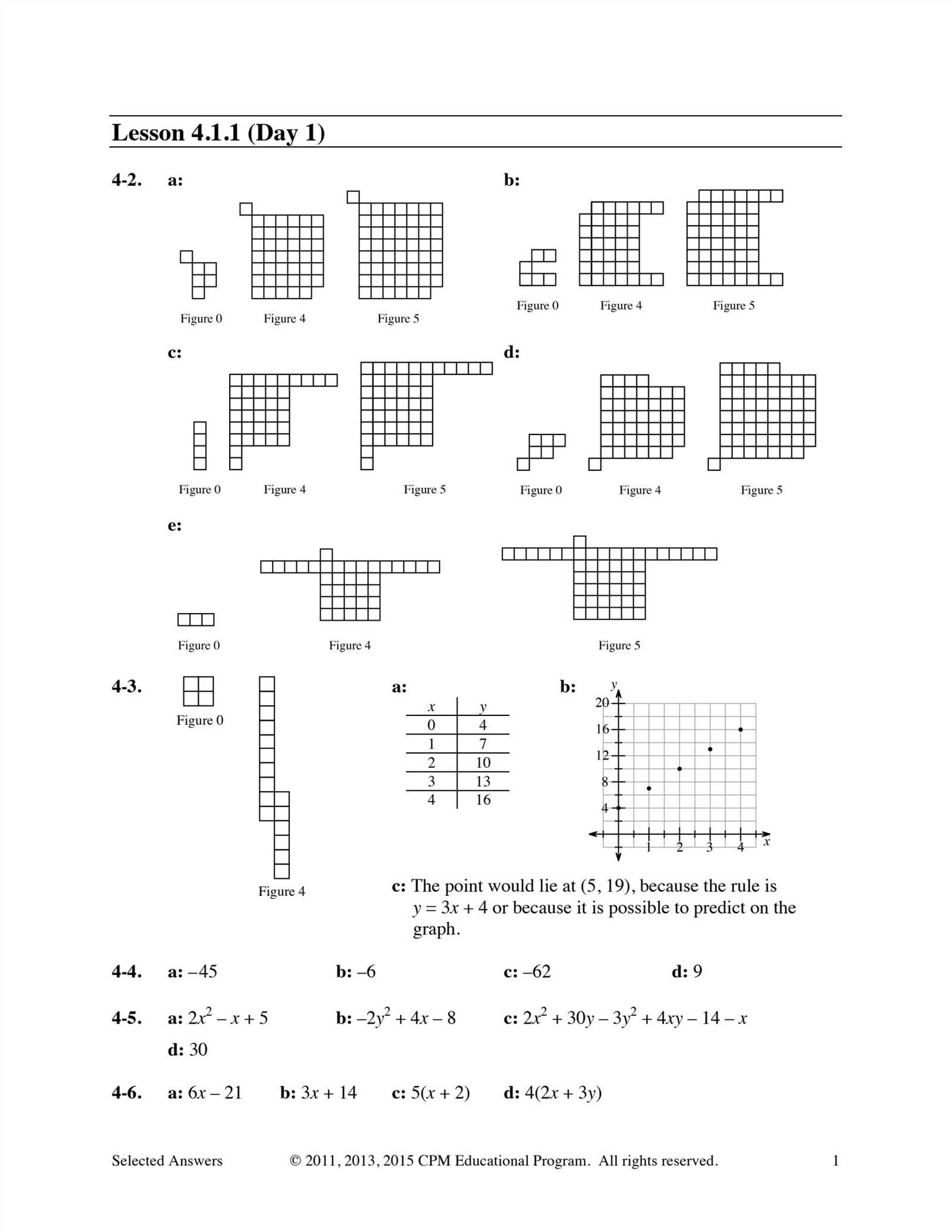
This section focuses on the process of plotting straight-line relationships on a coordinate plane. By understanding the equation of a line, you can visually represent the relationship between two variables. Graphing these functions helps to reveal patterns and trends, making it easier to interpret data and solve real-world problems.
To graph a linear function, it is essential to identify the slope and the y-intercept from the equation. The slope indicates the steepness of the line, while the y-intercept tells you where the line crosses the vertical axis. Once these key components are determined, you can plot points and draw the line, which represents the function’s behavior.
Understanding Mathematical Operations
This section delves into the fundamental operations used in solving mathematical problems. Understanding how to manipulate numbers and variables is key to solving equations and expressing relationships. These operations form the foundation for all higher-level math concepts, so mastering them is essential for success.
The primary operations include addition, subtraction, multiplication, and division. Each of these operations has its own set of rules and properties that must be understood in order to solve problems correctly and efficiently.
Key Mathematical Operations
- Addition – Combining two or more numbers to find their total.
- Subtraction – Determining the difference between two numbers.
- Multiplication – Repeated addition of the same number.
- Division – Splitting a number into equal parts.
Order of Operations

- Start with operations inside parentheses.
- Perform exponents and roots (if any).
- Follow with multiplication and division from left to right.
- Finally, perform addition and subtraction from left to right.
Finding Unknown Values in Equations
This section focuses on solving equations where certain values are unknown. The goal is to isolate the unknown variable and determine its value using logical steps. By understanding the structure of the equation and applying the correct operations, you can uncover the value that satisfies the equation.
The process of finding unknowns often involves manipulating the equation to simplify it and isolate the variable of interest. This may include using inverse operations, such as addition and subtraction, or multiplication and division, to eliminate other terms and solve for the unknown.
Using Substitution and Elimination
This section covers two key methods for solving systems of equations: substitution and elimination. Both techniques help find the values of variables that satisfy multiple equations simultaneously. By mastering these approaches, you can solve complex problems involving two or more unknowns with greater efficiency.
Substitution involves solving one equation for a variable and then substituting that expression into another equation to solve for the remaining variable. Elimination, on the other hand, involves adding or subtracting equations to eliminate one variable, allowing you to solve for the other.
Substitution Method
- Start by solving one equation for one variable.
- Substitute the expression into the other equation.
- Solve the second equation for the remaining variable.
- Substitute the value of the found variable back into the first equation to find the other variable.
Elimination Method
- Align the equations so that the coefficients of one variable are the same or opposites.
- Add or subtract the equations to eliminate one variable.
- Solve for the remaining variable.
- Substitute the found value back into one of the original equations to determine the other variable.
Real-Life Applications of Algebra
The concepts explored in this section are not only essential for solving mathematical problems but also play a crucial role in everyday life. From budgeting to making business decisions, the skills acquired in this area are widely applicable and help individuals solve practical problems efficiently. Understanding how mathematical relationships work allows us to make informed decisions in various real-world situations.
Common Applications
- Financial Planning: Using equations to calculate expenses, savings, and investment growth.
- Engineering: Applying formulas to design structures, analyze forces, and solve mechanical problems.
- Shopping: Comparing prices, applying discounts, and calculating total costs with taxes.
- Technology: Algorithms and coding often rely on mathematical principles to solve problems and create software.
Practical Examples
- Budgeting: You can use equations to plan and manage household or business expenses over time.
- Cooking: Adjusting ingredient quantities for recipes based on the number of servings required can be modeled using ratios and equations.
- Traveling: Estimating travel time, fuel costs, or the total distance covered involves applying simple mathematical operations.
CPM Algebra 1 Chapter 1 Review
This section provides a comprehensive overview of the fundamental concepts covered earlier. The goal is to reinforce the key principles and techniques, ensuring a solid understanding of how to approach problems effectively. By reviewing these topics, learners can assess their understanding and identify areas for further practice.
Key Topics Covered
- Understanding and simplifying mathematical expressions.
- Solving equations and finding unknown values.
- Graphing linear relationships and interpreting data.
- Using substitution and elimination methods to solve systems of equations.
Review Tips
- Practice solving various types of equations to reinforce problem-solving skills.
- Focus on understanding the underlying concepts rather than memorizing steps.
- Utilize real-world examples to better grasp the application of these techniques.
- Collaborate with peers or seek additional resources for clarification on complex topics.