
Exploring educational resources designed for young learners can significantly enhance their understanding and confidence in tackling various topics. These materials serve as a bridge to clarify complex ideas, ensuring learners grasp essential concepts effectively.
In this article, we delve into helpful materials tailored for fifth-level students, providing insights and tips to make the learning journey smoother. By utilizing these tools, both students and parents can better navigate challenging subjects and build a strong foundation for future success.
Discover strategies for approaching learning tasks efficiently, and uncover methods to ensure students retain knowledge and develop problem-solving skills. This guide aims to simplify the process, making it accessible and engaging for everyone involved.
Understanding the Structure of Go Math
A well-organized learning tool can significantly enhance comprehension by presenting content in a clear and systematic manner. The arrangement of topics and activities ensures that learners can follow a logical progression as they build their skills.
The framework of these materials typically includes several important features:
- Step-by-Step Layout: Concepts are introduced progressively, allowing students to grasp foundational ideas before moving to more advanced topics.
- Illustrative Problems: Visual aids and examples help clarify complex ideas, making them easier to understand.
- Practice Sections: Exercises and activities are included to reinforce understanding and encourage critical thinking.
- Assessment Tools: Quizzes and review sections help track progress and identify areas for improvement.
This structured approach creates a supportive environment where students can confidently tackle new challenges, ensuring steady growth and a deeper understanding of the subject matter.
Key Features of Grade 5 Math Book
Learning tools designed for this level often include structured components that cater to the developmental needs of young learners. These features aim to promote understanding, engagement, and independent problem-solving skills.
Organized Content Presentation
- Logical Topic Flow: Concepts are introduced in a sequence that builds on prior knowledge, helping learners connect ideas.
- Clear Explanations: Each section includes straightforward descriptions to ensure clarity and reduce confusion.
- Diverse Activities: Exercises vary from simple tasks to complex challenges, fostering skill development across different areas.
Supportive Learning Elements
- Visual Resources: Illustr
How to Use Practice Books Effectively
Effective learning requires a strategic approach to using educational resources. By focusing on proper techniques and consistent engagement, learners can maximize the benefits of their study materials.
Create a Structured Routine
- Set Clear Goals: Outline specific objectives for each study session to stay focused and organized.
- Allocate Time Wisely: Dedicate regular, manageable time slots to work through exercises without feeling overwhelmed.
- Review Progress: Periodically revisit previous sections to reinforce understanding and track improvements.
Engage with the Content Actively
- Analyze Examples: Study provided examples carefully to understand the logic and reasoning behind each solution.
- Practice Consistently: Complete exercises regularly to build confidence and reinforce new skills
Common Challenges in Fifth Grade Math
As students progress in their studies, they often encounter certain obstacles that can impede their understanding of complex concepts. These challenges typically arise from the increasing difficulty of the material, requiring a more advanced level of reasoning and problem-solving skills.
Key Areas of Difficulty
Area of Difficulty Reason for Challenge Fractions and Decimals Understanding the relationship between fractions and decimals and performing conversions can be confusing for many learners. Word Problems Applying mathematical concepts to real-life scenarios requires critical thinking and careful interpretation of the problem. Multi-Step Operations Executing multi-step operations correctly can be overwhelming, especially when multiple concepts are involved. Geometry Understanding shapes, angles, and spatial relationships requires visual and spatial reasoning skills, which can be challenging. How to Overcome These Challenges
- Practice Regularly: Repetition helps solidify concepts and reduce errors, particularly with more complex topics like fractions and operations.
- Visualize Problems: Using diagrams and visual aids can make abstract concepts like geometry and fractions easier to understand.
- Break Down Problems: For multi-step problems, break them into smaller, manageable parts to ensure a clearer understanding and reduce the chance of mistakes.
By addressing these common obstacles and adopting effective strategies, students can build confidence and overcome difficulties in their studies.
Strategies to Solve Problems

To approach complex tasks effectively, learners need to apply specific methods that help them break down and understand the problem at hand. These strategies enable students to tackle various challenges with clarity and confidence.
Step-by-Step Breakdown
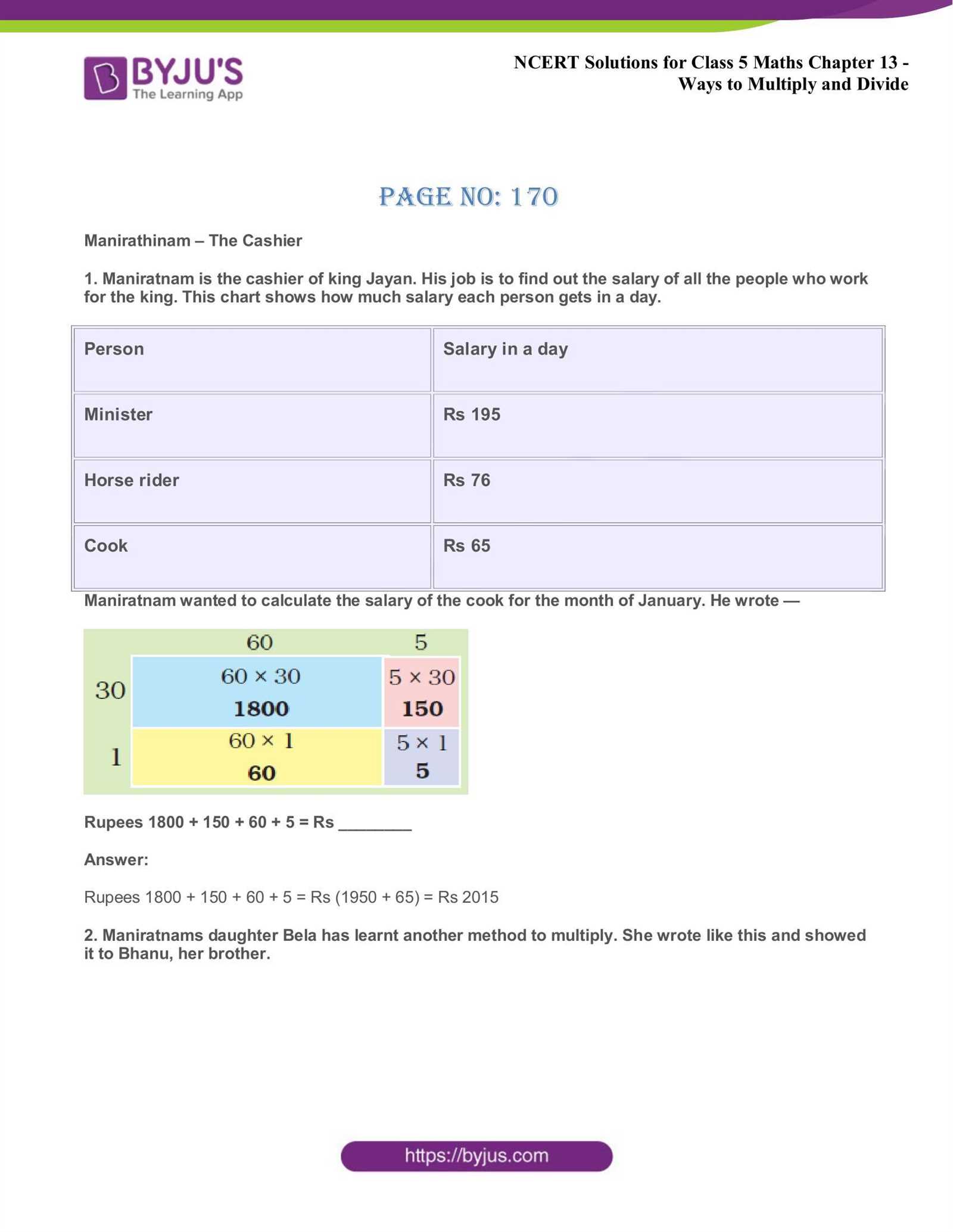
- Understand the Problem: Carefully read the problem to identify the key information and what is being asked.
- Plan a Solution: Think about the steps required to find the solution. Consider using visual aids, such as diagrams or tables, to organize the data.
- Execute the Plan: Follow the steps logically, checking each one to ensure no errors are made along the way.
- Review the Solution: After reaching the answer, go back through the steps to confirm the correctness of the solution and ensure all aspects were addressed.
Using Mental Strategies
- Estimation: Before solving a problem, make an educated guess about the answer to help guide your work and ensure it’s within a reasonable range.
- Identify Patterns: Look for recurring patterns in numbers or relationships that can simplify the solution process.
- Use Logical Reasoning: Use deductive reasoning to eliminate incorrect possibilities and narrow down potential solutions.
By incorporating these strategies, learners can approach problems with more precision and enhance their ability to solve challenges efficiently.
Benefits of Standards-Based Learning
Adopting a framework that aligns with specific learning goals offers clear advantages for both students and educators. This structured approach helps guide the educational process and ensures consistent progress toward mastery of key concepts.
Clear Learning Objectives
With clearly defined expectations, students understand exactly what is expected of them at each stage of their educational journey. This clarity provides a sense of direction and helps them stay focused on achieving specific milestones.
- Consistency: Ensures that all learners receive the same core content, regardless of location or teaching style.
- Focused Learning: Students concentrate on mastering particular skills before moving on to more complex topics, building a solid foundation for future learning.
Enhanced Student Performance

When learners follow a structured approach, they can gradually develop and refine their skills. This leads to measurable progress, as their understanding deepens with each achievement. Additionally, teachers can more easily identify areas where students may need additional support.
- Progress Tracking: Teachers can assess students’ abilities more effectively, ensuring that each individual’s development is closely monitored.
- Improved Outcomes: Research shows that students in environments with clear learning benchmarks often achieve better results compared to those with less defined goals.
Overall, this method fosters a more organized and measurable learning environment, benefiting students by providing clear goals and steady progress toward mastering key skills.
How to Find Accurate Solutions

Finding precise solutions to problems requires a systematic approach. By following structured steps and applying problem-solving techniques, students can ensure they reach the correct outcome. The key to accuracy lies in understanding the problem fully and using the right methods to solve it.
Steps for Solving Problems Accurately
Before diving into solving any problem, it’s crucial to break it down into manageable parts. This helps identify the necessary tools and strategies for finding the right solution. Below are the essential steps to take:
- Understand the Problem: Carefully read the problem to ensure you understand what is being asked. Identify key information such as numbers, operations, and specific requirements.
- Plan the Solution: Decide on the most effective strategy for solving the problem. This could involve selecting a method, formula, or approach that is best suited to the situation.
- Perform Calculations: Execute the necessary calculations step by step, ensuring that each operation is carried out correctly.
- Check the Solution: After obtaining an answer, review the steps and the final result. Verify if the solution makes sense in the context of the original problem.
Common Techniques for Ensuring Accuracy
There are several methods that can be used to help verify and ensure the accuracy of a solution:
- Double-Check Work: Revisit the problem and solution after completing the steps to ensure there were no errors in the calculations or reasoning.
- Use Estimation: Estimation can serve as a quick check. If your final answer seems far from the estimated value, it’s worth re-evaluating the process.
- Seek Multiple Methods: Sometimes trying a different approach can help confirm the result. If different methods lead to the same answer, it increases confidence in its accuracy.
By adhering to these guidelines, learners can strengthen their problem-solving skills and increase the likelihood of finding accurate results.
Exploring Concepts in Go Math Curriculum
The curriculum designed for early education introduces essential ideas and strategies to enhance problem-solving abilities. Understanding these core concepts helps learners build a strong foundation for future learning. By exploring a variety of topics, students can develop critical thinking skills and improve their analytical abilities.
Key concepts are carefully chosen to ensure a balanced development of skills. These include numerical operations, understanding patterns, and applying logic in various scenarios. Each concept is connected to real-world examples to make the learning process engaging and relevant.
Concept Key Focus Example Number Operations Addition, subtraction, multiplication, division Solving equations with various operations Patterns and Sequences Identifying patterns and predicting the next number Finding the next number in a sequence like 2, 4, 6, 8 Fractions and Decimals Understanding parts of a whole and converting between fractions and decimals Expressing 1/2 as 0.5 or 50% Geometry Shapes, areas, perimeters, and volumes Calculating the area of a rectangle or the perimeter of a square By delving deeper into each concept, students can connect their learning to practical applications and enhance their understanding. The curriculum also emphasizes problem-solving strategies, helping students approach challenges methodically and efficiently.
Improving Skills with Practice

Repetition and active engagement are crucial when it comes to strengthening problem-solving abilities. Regular exercises help solidify concepts, making them easier to recall and apply in different scenarios. Mastery of various techniques comes with consistent practice, reinforcing skills and boosting confidence in tackling challenges.
To enhance understanding, it is essential to engage in exercises that span different levels of difficulty. Gradually increasing the complexity ensures that learners build a strong foundation and progress toward more advanced tasks. Active participation also fosters a deeper comprehension of underlying principles.
Effective Methods for Enhancing Skills
- Consistent Practice: Repeating exercises regularly helps reinforce key concepts and develop a strong grasp of the material.
- Breaking Down Problems: Tackling problems step-by-step can prevent overwhelm and ensure better understanding of each part of the process.
- Varied Approaches: Exploring different ways to solve a problem can provide a deeper insight into the subject and offer alternative solutions.
Tracking Progress

Tracking progress is essential for recognizing improvements and areas that need further attention. By regularly assessing strengths and weaknesses, learners can focus on specific areas that require additional effort. This helps ensure that each concept is fully understood and retained.
Where to Access Reliable Answer Keys
Having access to trustworthy solutions is an essential part of evaluating progress and ensuring a correct understanding of various topics. Accurate guides can help verify the work completed, offering learners a way to check their reasoning and identify any mistakes. These resources serve as an important tool for learning, allowing students to make adjustments and improve their techniques.
There are multiple ways to find dependable solution keys, both online and offline. Some resources provide full explanations for each problem, while others may offer concise solutions. Below are some popular options for accessing these helpful materials.
Reliable Sources for Solution Keys
- Official Educational Websites: Many educational institutions provide resources that include verified solution sets for their materials, offering a high level of accuracy and consistency.
- Teacher Resources: Educators often have access to detailed solution guides that can be shared or referenced when available.
- Academic Forums and Communities: Online forums where learners and instructors discuss problems often feature collaborative solutions and detailed explanations, providing multiple perspectives on how to approach challenges.
- Educational Publishers: Publishers that produce learning materials typically offer solution sets for purchase or through supplementary digital tools linked to their resources.
By using these trusted sources, students can ensure that they are following correct methodologies and improving their skills through well-supported resources.
Math Problem Types in Grade 5
At this level, learners encounter various types of challenges that are aimed at strengthening their problem-solving abilities. These exercises require the application of fundamental concepts to solve complex scenarios. The problems are structured to progressively enhance students’ analytical skills, covering a wide range of operations, shapes, and real-world applications. Understanding different problem types is essential for developing critical thinking and approaching tasks with confidence.
Common Problem Categories
In this stage, students are exposed to a variety of problem types that test their understanding and calculation abilities. These problems often include, but are not limited to, the following categories:
- Real-World Problems: These require learners to interpret and solve situations from everyday life, often involving several steps.
- Fraction Operations: These problems involve performing operations like addition, subtraction, multiplication, and division with fractions.
- Decimal Calculations: Exercises that involve working with decimal numbers, including addition, subtraction, and multiplication.
- Unit Conversions: Tasks that challenge students to convert units of measurement, such as length, weight, or volume.
- Geometric Applications: Problems that involve shapes, area, volume, and perimeter calculations.
Sample Problem Types
Problem Type Example Skills Tested Real-World Problem If a bus departs at 10 AM and travels for 3 hours, what time will it arrive? Time calculation and reasoning Fraction Operations What is 2/5 + 3/10? Adding fractions with different denominators Decimal Calculations Subtract 7.25 from 12.50. Decimal subtraction Unit Conversions Convert 3 meters to centimeters. Understanding unit conversions Geometric Applications Find the area of a triangle with a base of 8 cm and height of 5 cm. Area calculation These problem types provide students with opportunities to develop their reasoning, calculation, and critical thinking abilities. Mastery of these concepts is crucial for further academic success and for applying skills in real-world situations.
Tips for Parents Supporting Learning
Parents play a crucial role in fostering a positive and effective learning environment at home. With the right support and guidance, students can develop strong problem-solving skills and a deep understanding of essential concepts. By providing encouragement, resources, and consistent involvement, parents can help their children navigate challenges and build confidence in their abilities. Below are a few practical tips for parents looking to support their child’s academic growth effectively.
- Encourage a Growth Mindset: Emphasize effort and persistence over immediate success. Encouraging children to embrace challenges and learn from mistakes helps them develop resilience.
- Make Learning Interactive: Use everyday situations, such as cooking or shopping, to reinforce concepts. This makes learning more engaging and applicable to real-life scenarios.
- Create a Routine: Establish a regular study schedule that provides consistency and structure. Consistency helps children build focus and stay organized.
- Ask Open-Ended Questions: Instead of simply providing answers, ask questions that encourage your child to think critically and explain their reasoning. This helps improve their problem-solving skills.
- Be Patient: Learning complex concepts can take time. Show patience and understanding when your child struggles, and offer support when needed.
- Provide Positive Reinforcement: Celebrate achievements, no matter how small, to boost your child’s motivation and self-esteem. Recognizing progress encourages a positive attitude toward learning.
By adopting these strategies, parents can create a supportive environment that promotes confidence and a love for learning. Your involvement can make a significant difference in your child’s academic journey.
Best Practices for Self-Assessment in Learning
Self-assessment is an important skill that encourages students to reflect on their own understanding and progress. It enables learners to identify strengths and areas for improvement while promoting independence and responsibility in their academic journey. By regularly evaluating their own work, students gain valuable insight into their learning process and develop strategies to enhance their performance. Below are some effective methods for conducting self-assessments that can lead to better learning outcomes.
1. Set Clear Goals and Objectives

Before beginning any task or assignment, it’s essential for students to set specific, measurable goals. These goals should be focused on the key skills or concepts being learned. By having a clear sense of direction, students can better assess whether they’ve achieved their objectives and identify areas that require more focus.
2. Use Rubrics for Evaluation
Rubrics provide a structured framework for evaluating work based on set criteria. When students use rubrics for self-assessment, they can break down the requirements of the task and evaluate each aspect of their performance. This practice encourages detailed reflection and helps ensure that students understand what is expected of them.
3. Reflect on Mistakes and Successes
Encouraging students to reflect on both mistakes and successes is essential for growth. By understanding why certain approaches worked and others didn’t, learners can adapt their strategies and improve their problem-solving skills. Reflection is key to developing a deeper understanding of the material.
4. Keep a Learning Journal
A learning journal can be a valuable tool for self-assessment. Students can use it to track their progress, jot down what they’ve learned, and note any areas where they still feel unsure. Regularly reviewing the journal allows learners to see how far they’ve come and which areas need further attention.
5. Seek Feedback and Compare Results
Self-assessment becomes even more effective when combined with feedback from others. By comparing their self-assessment with teacher or peer feedback, students can refine their evaluation process and gain new perspectives on their performance.
By adopting these best practices, students can develop greater awareness of their own learning processes, leading to improved academic outcomes and greater confidence in their abilities.
Aligning Educational Resources with School Requirements
Integrating educational tools with the requirements set by educational systems is crucial for ensuring that students receive a well-rounded and standardized learning experience. When instructional materials are aligned with these expectations, they help students acquire the necessary skills and knowledge needed to succeed. The key is to ensure that the resources used in the classroom effectively cover the required topics while promoting understanding and critical thinking.
1. Identifying Core Competencies
One of the first steps in aligning instructional resources with educational frameworks is identifying the core competencies that students are expected to master. These competencies outline the key skills and knowledge that students need to develop at each stage of their learning journey. By ensuring that educational tools target these competencies, educators can provide students with the right resources to build a strong foundation.
2. Mapping Lessons to Learning Goals
Each lesson or unit should be mapped to specific learning objectives outlined in the curriculum. When resources are designed with these goals in mind, they provide students with focused activities and assessments that allow them to meet the expected outcomes. This approach helps ensure that students progress in a structured manner and that each learning experience is purposeful and relevant.
3. Continuously Reviewing and Adapting Content

Educational needs and requirements evolve, so it’s essential to regularly review and adapt instructional content. By keeping up with updates to curriculum guidelines, educators can ensure that their teaching materials remain aligned with the latest expectations. This process helps to maintain the effectiveness and relevance of the resources used in the classroom.
Aligning instructional resources with educational expectations not only supports the academic success of students but also ensures that teachers are equipped with tools that enhance the learning experience. By focusing on core competencies, mapping lessons to specific goals, and continuously adapting content, educators can foster an environment where students thrive and meet their learning targets.
Interactive Ways to Learn Fifth Grade Concepts
Engaging students through interactive activities can make learning both enjoyable and effective. When students actively participate in their learning journey, they are more likely to retain the information and develop a deeper understanding of the material. Interactive methods can range from hands-on activities to technology-driven tools that allow students to experiment, explore, and reinforce their knowledge in a fun and dynamic way.
1. Educational Games
Games provide a stimulating environment where students can practice skills while enjoying the process. Whether through board games, card games, or digital platforms, educational games offer a variety of opportunities for students to engage with core concepts. These activities often include challenges and rewards that keep learners motivated.
- Online quizzes with instant feedback
- Interactive puzzles and brain teasers
- Game-based apps to reinforce skills
2. Hands-On Learning Activities
Using physical materials in the classroom or at home allows students to see abstract ideas come to life. This can help make difficult concepts more tangible and relatable. Activities like building models, using manipulatives, or conducting simple experiments can spark curiosity and help students visualize their learning.
- Building geometric shapes with sticks and clay
- Measuring objects with rulers and tape
- Creating graphs with real-world data (e.g., weather patterns)
By incorporating interactive methods, students gain the chance to apply their knowledge in real-world scenarios, making the learning experience more meaningful and impactful. These techniques not only enhance engagement but also improve critical thinking and problem-solving skills.
Common Core Alignment in Go Math
Ensuring that a curriculum aligns with educational benchmarks is essential for providing students with a structured and consistent learning experience. A well-aligned curriculum helps educators track progress, identify areas for improvement, and deliver targeted instruction. When lessons and activities match key learning goals, students gain the necessary skills to advance confidently through their academic journey.
Key Areas of Focus
The alignment with educational frameworks ensures that all students are exposed to critical concepts at the appropriate time. These frameworks emphasize problem-solving, analytical thinking, and the application of learned concepts in real-world scenarios. Here’s how these goals are reflected in a structured curriculum:
Focus Area Key Objective Expected Outcome Problem Solving Encourages students to apply strategies to solve real-world issues Students demonstrate the ability to approach complex challenges with confidence Concept Understanding Strengthens the grasp of fundamental ideas Students internalize core concepts and apply them in various contexts Application of Knowledge Promotes the use of learned skills in practical situations Students show proficiency in using acquired knowledge beyond the classroom Ensuring Consistency Across Lessons
Through well-thought-out alignment, each lesson builds upon the previous one, ensuring continuity and deepening understanding. Teachers can focus on mastering key concepts while also offering differentiated support for students who may need additional assistance. This alignment is integral to helping students achieve the necessary proficiency at each stage of their educational journey.
Mastering Concepts Through Practice
Reinforcing foundational ideas through continuous engagement is key to achieving proficiency. Consistent exposure to various problem types allows learners to internalize concepts and apply them effectively. Regular exercises, whether they are structured or exploratory, provide opportunities for growth, helping to solidify knowledge and boost confidence in handling new challenges.
Why Repetition is Essential
Repetition allows students to solidify their understanding and discover new ways to approach familiar problems. It fosters deeper insight into how different principles interconnect and can be applied across a variety of situations. Here are some benefits of consistent practice:
- Retention: Repeated engagement with a topic improves long-term memory.
- Confidence: Overcoming challenges through practice boosts self-assurance in tackling unfamiliar tasks.
- Fluency: Regular exercises enhance speed and accuracy, enabling students to solve problems more efficiently.
- Mastery: Repeated exposure to varying complexities ensures complete understanding of concepts.
Effective Practice Strategies
While repetition is important, practicing with purpose is equally essential. Focusing on specific areas of difficulty and progressively increasing the complexity of tasks helps in mastering challenging topics. Here are a few effective strategies:
- Break down problems: Divide complex tasks into smaller, manageable parts to understand each step.
- Use real-world examples: Apply learned concepts to everyday scenarios to demonstrate practical usage.
- Seek feedback: Discuss mistakes and misunderstandings to improve comprehension and technique.