The second section of this curriculum focuses on developing critical mathematical reasoning and problem-solving abilities. By tackling a variety of challenges, students are introduced to the fundamentals of equations, expressions, and their relationships. This approach allows learners to strengthen their understanding of mathematical structures and apply these skills to solve complex problems.
Throughout this section, students will encounter various techniques to simplify and solve problems. These techniques help build a strong foundation for more advanced topics, ensuring that key concepts are fully understood. With clear examples and practice exercises, learners can gradually build confidence and gain mastery over the material.
Mastering these skills is crucial not only for academic success but also for everyday problem-solving. Whether working through assignments or applying logic in real-world scenarios, the principles learned here provide the tools necessary for continued growth in mathematics.
Understanding the Key Concepts in Section 2
This section introduces fundamental mathematical ideas essential for building a strong foundation in solving numerical problems. It emphasizes techniques for analyzing and manipulating different expressions, focusing on enhancing problem-solving strategies. Students will gain insight into how to approach mathematical challenges methodically and efficiently.
Breaking Down Core Techniques
The main focus is on mastering methods for simplifying equations and understanding their relationships. By applying these techniques to a range of exercises, learners are encouraged to recognize patterns and develop a deeper understanding of how different mathematical elements interact with each other. This process helps in strengthening reasoning skills and builds confidence in solving progressively difficult tasks.
Practical Applications of Mathematical Methods
Once the basic principles are understood, students can start applying these methods to real-world problems. These practical applications help bridge the gap between theory and practice, showing how mathematical reasoning can be useful in various everyday situations. Whether in academics or personal decision-making, the skills learned here are applicable across many areas of life.
Overview of Section 2

This section focuses on developing essential mathematical skills by exploring key concepts that form the basis of more advanced problem-solving. It covers a range of topics that teach students how to work with different types of expressions and equations, helping them build a solid foundation for future learning. By engaging with various problems, learners improve their ability to approach and solve complex tasks efficiently.
Main Concepts Covered
- Understanding the structure of equations
- Learning to manipulate expressions effectively
- Identifying patterns and relationships between terms
- Applying basic strategies for solving problems
Skills Developed in This Section
- Improved ability to simplify and solve equations
- Enhanced critical thinking and problem-solving techniques
- Better understanding of how mathematical concepts connect
- Greater confidence in approaching various mathematical challenges
Key Concepts in Section 2
This section introduces crucial ideas that form the foundation for tackling mathematical problems. It explores the relationships between different mathematical elements and how they can be used together to solve complex tasks. By mastering these core concepts, students can develop a stronger understanding of mathematical reasoning and improve their problem-solving abilities.
Core Ideas Covered
- Identifying and working with variables and constants
- Understanding the structure of expressions and equations
- Applying techniques for simplifying and solving equations
- Recognizing patterns in mathematical problems
Developing Essential Skills
- Enhancing the ability to manipulate mathematical terms
- Building stronger problem-solving strategies
- Improving analytical thinking and reasoning
- Learning to apply abstract concepts to real-world situations
How to Approach Mathematical Problems
Successfully solving mathematical problems requires a structured approach that breaks down each task into manageable steps. By following a logical sequence, learners can simplify complex equations and identify the best strategies for reaching solutions. This method helps avoid common mistakes and improves accuracy in problem-solving.
Step-by-Step Process for Solving Problems
| Step | Description |
|---|---|
| 1. Understand the Problem | Read the problem carefully and identify the known and unknown values. |
| 2. Translate to Mathematical Language | Convert words and phrases into mathematical expressions or equations. |
| 3. Simplify the Equation | Apply basic operations to simplify the equation or expression. |
| 4. Solve for the Variable | Isolate the variable and solve for its value. |
| 5. Check the Solution | Substitute the solution back into the original equation to verify it works. |
Tips for Effective Problem Solving
- Always double-check your calculations.
- Look for patterns that can simplify the process.
- Take your time to understand each part of the problem.
- Practice regularly to build confidence and speed.
Step-by-Step Solutions for Section 2
Breaking down problems into smaller, manageable steps is essential for mastering mathematical tasks. By following a structured process, learners can ensure they understand each part of the problem and approach the solution systematically. This section provides detailed steps for solving the key problems presented, offering clear guidance to enhance comprehension and accuracy.
Detailed Problem-Solving Approach
| Step | Description |
|---|---|
| 1. Analyze the Problem | Read through the problem and identify the values and unknowns. Make sure to understand what is being asked. |
| 2. Set Up the Equation | Translate the problem into a mathematical equation or expression that can be worked with. |
| 3. Simplify the Expression | Combine like terms and apply any necessary operations to simplify the equation. |
| 4. Solve for the Unknown | Isolate the variable to find its value, using appropriate mathematical techniques. |
| 5. Verify the Solution | Substitute the solution back into the original equation to ensure it satisfies all conditions. |
Common Mistakes to Avoid
- Skipping steps or rushing through calculations.
- Forgetting to check the solution after solving.
- Misinterpreting the problem or setting up the wrong equation.
- Overcomplicating simple problems.
Solving Linear Equations Effectively
Mastering the art of solving linear equations is essential for developing a strong foundation in mathematics. By following a clear and systematic approach, you can quickly and efficiently isolate the variable and find the solution. This process involves applying basic operations, such as addition, subtraction, multiplication, and division, to simplify the equation step by step.
Step-by-Step Guide to Solving Linear Equations

| Step | Description |
|---|---|
| 1. Simplify Both Sides | Start by simplifying both sides of the equation. Combine like terms where possible. |
| 2. Eliminate Constants | Move constant values to one side of the equation using addition or subtraction. |
| 3. Isolate the Variable | Use multiplication or division to isolate the variable on one side of the equation. |
| 4. Solve for the Variable | Perform the final operation to find the value of the variable. |
| 5. Check the Solution | Substitute the solution back into the original equation to ensure it satisfies both sides. |
Tips for Efficient Problem Solving
- Always combine like terms first to make equations simpler.
- Be careful with signs when moving terms from one side to the other.
- Double-check each step to avoid calculation errors.
- Practice with various types of problems to increase your speed and confidence.
Identifying Patterns in Algebraic Expressions
Recognizing patterns within mathematical expressions is a key skill in solving problems efficiently. By identifying recurring structures and relationships, you can simplify expressions and make calculations quicker. These patterns often reveal valuable insights into the behavior of variables and constants, allowing for more straightforward solutions and predictions.
Common Types of Patterns in Expressions
There are several types of patterns that can appear in mathematical expressions. These include:
- Linear Relationships: Expressions where the variable is raised to the first power, such as 3x + 5.
- Quadratic Forms: Patterns where the variable is squared, such as x² + 4x + 3.
- Factorable Expressions: Expressions that can be factored into simpler binomials or polynomials, like x² – 9 (which factors to (x – 3)(x + 3)).
How to Recognize and Use Patterns
To effectively use patterns, start by looking for similarities in terms and coefficients. For example, in an equation with repeated terms or factors, it may be possible to simplify the expression by factoring or combining like terms. Recognizing these patterns not only speeds up problem-solving but also strengthens your understanding of how different expressions relate to one another.
Common Mistakes in Chapter 2 and Fixes
When working through mathematical problems, it’s easy to make errors, especially when dealing with complex expressions and equations. Recognizing common mistakes is crucial for improving your problem-solving skills and avoiding unnecessary setbacks. By understanding where things typically go wrong, you can apply strategies to correct them and approach problems with more confidence.
Frequent Errors and How to Correct Them
- Incorrect Distribution: One common mistake is failing to distribute a term across a sum or difference properly. To avoid this, always double-check your multiplication steps to ensure each term is distributed correctly.
- Combining Unlike Terms: Another frequent error is mistakenly adding or subtracting terms that don’t have the same variable or exponent. Remember, only like terms can be combined. Pay attention to the variables and exponents before simplifying.
- Sign Errors: Mistaking the sign of a number when adding or subtracting is a common issue. Be cautious with negative numbers and consider using parentheses to clarify operations.
Preventing These Mistakes
To avoid these common errors, it’s helpful to work through each problem step by step, carefully verifying each operation. Use a methodical approach, and when in doubt, rewrite the equation to ensure you’re following the correct procedures. Taking extra time to check your work can save significant effort in the long run and help you gain more confidence in your skills.
Strategies for Improving Algebra Skills
Enhancing your mathematical skills requires consistent practice and the adoption of effective strategies. Whether you’re tackling complex equations or learning new concepts, having a clear plan in place can significantly improve your proficiency. By understanding the core concepts and developing a systematic approach, you can make steady progress and gain more confidence in solving problems.
Focus on Understanding Core Concepts
Instead of memorizing formulas or shortcuts, focus on understanding the fundamental principles behind the operations. This deep understanding will allow you to apply your knowledge to different types of problems. Practice consistently by working through examples and asking questions when you encounter challenges. The more you grasp the core ideas, the easier it becomes to navigate complex equations.
Utilize Effective Study Techniques
- Practice Regularly: The more you practice, the more familiar the problems become. Start with easier problems and gradually move to more challenging ones as your confidence builds.
- Break Down Problems: If you encounter a difficult problem, break it down into smaller, manageable parts. This helps prevent feeling overwhelmed and makes it easier to solve.
- Seek Help When Needed: Don’t hesitate to ask for help if you’re stuck. Whether it’s a teacher, tutor, or peer, getting guidance from others can help you understand the material from a different perspective.
By adopting these strategies, you’ll be able to strengthen your problem-solving skills and improve your overall performance in mathematical tasks.
Detailed Explanation of Chapter 2 Exercises
Understanding how to approach and solve problems is crucial for mastering any mathematical concept. In this section, we will go over the exercises from the second unit, providing clear and detailed explanations to ensure you grasp each idea fully. By breaking down the steps involved, you will see how to apply various techniques and solve problems more effectively.
The exercises in this section focus on building a solid foundation in problem-solving strategies. Each problem is designed to reinforce key concepts, such as solving linear equations, recognizing patterns, and applying basic mathematical operations. We will explore step-by-step methods that make each problem easier to tackle.
Step 1: Understanding the Problem
Before diving into solving any problem, it’s important to first understand what is being asked. Carefully read each problem and identify the variables, constants, and relationships between them. This step will help you create a clear mental image of the problem, allowing you to focus on the solution.
Step 2: Applying the Right Method
After understanding the problem, choose the most appropriate method to solve it. Whether it’s isolating variables or simplifying expressions, applying the right approach can make a significant difference in solving the problem efficiently. Use methods such as substitution, elimination, or simplifying both sides of the equation to make progress toward finding the solution.
By following these steps, you can confidently tackle the exercises and reinforce your understanding of key concepts in the unit. Practice is essential, and by breaking down each problem methodically, you will become more proficient in solving similar problems in the future.
How to Prepare for Algebra 1 Tests
Preparing effectively for tests requires more than just memorizing formulas; it involves understanding core principles, practicing problem-solving techniques, and refining your ability to apply learned concepts in different scenarios. Proper preparation is key to performing well on any math exam, and with the right approach, you can approach your test with confidence.
Here are several strategies to help you prepare for an upcoming test:
Review Key Concepts
- Go over the most important topics covered in the lessons.
- Ensure you fully understand basic concepts, such as solving equations, simplifying expressions, and identifying patterns.
- Work through examples and make sure you can apply the concepts in different problem-solving situations.
Practice Problem-Solving
- Complete practice exercises and examples to reinforce your skills.
- Focus on problems you find difficult, and work through them multiple times to ensure you understand the solution process.
- Check your answers and understand any mistakes you make to avoid repeating them during the test.
Create a Study Schedule
- Plan out a study schedule in the days leading up to the test.
- Break down your study time into manageable chunks and focus on different sections each day.
- Don’t wait until the last minute–start early to give yourself enough time to review and practice.
By following these steps, you will be well-prepared for your test. Stay organized, practice regularly, and approach the test with a calm mindset for the best results. Consistent practice and a solid understanding of key concepts will ensure your success on the exam.
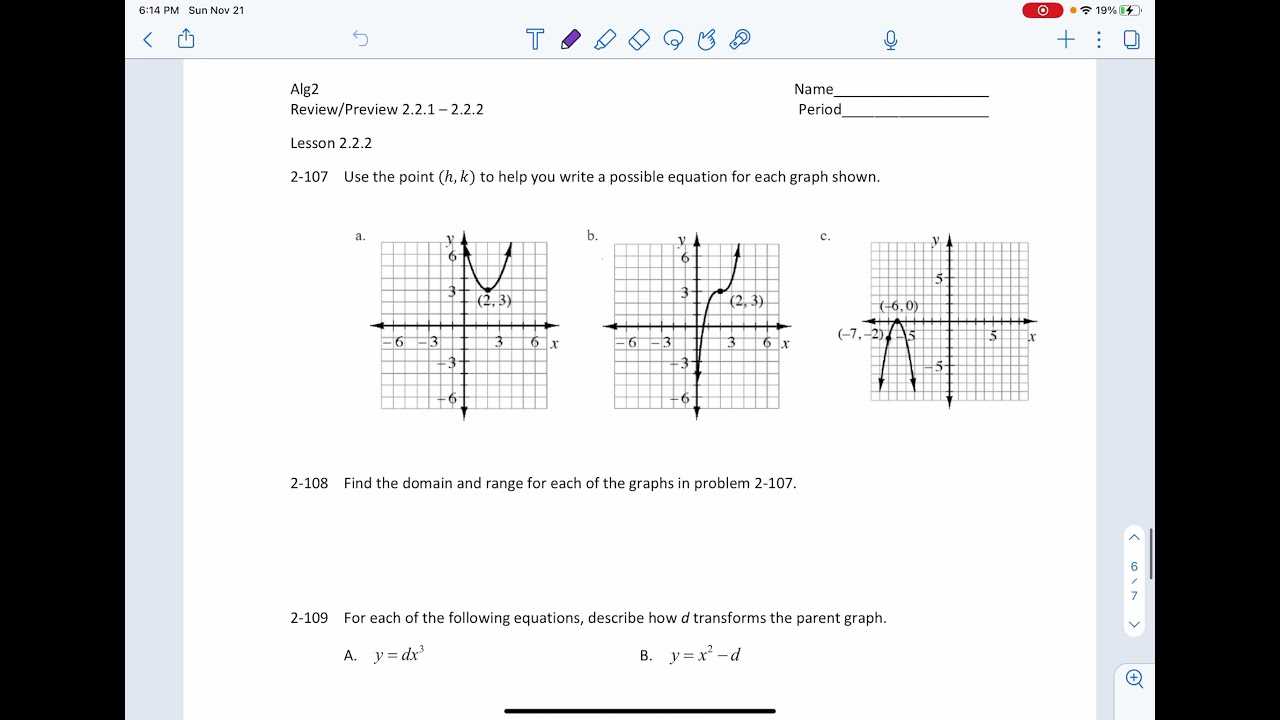
Using Graphs to Solve Algebraic Problems
Graphs are a powerful tool for visualizing mathematical relationships and solving problems. By representing equations or functions graphically, you can quickly identify key properties, such as solutions, intercepts, and trends. This visual approach simplifies the process of understanding how different variables interact and provides a clear picture of the problem at hand.
Understanding the Role of Graphs
Graphs allow you to see the relationship between variables in a visual format. For example, plotting linear equations on a coordinate plane helps you identify the slope, intercepts, and behavior of the equation. This is particularly useful for solving problems involving systems of equations, inequalities, and analyzing patterns in data.
Steps to Solve Problems Using Graphs
- Step 1: Plot the given equation or function on a graph by determining key points and drawing the line or curve that represents the relationship.
- Step 2: Analyze the graph to find important information, such as intercepts or points of intersection.
- Step 3: Use the graph to solve the problem, whether it’s finding a specific value, identifying the solution to a system of equations, or examining trends in the data.
By using graphs, you gain a deeper understanding of mathematical concepts and can approach problems with a more intuitive and visual mindset. This method is especially helpful in complex problems where numerical solutions might be harder to identify directly. With practice, graphing will become an indispensable skill for solving various types of mathematical challenges.
Practice Problems for Chapter 2 Mastery
Engaging in practice exercises is one of the most effective ways to reinforce concepts and gain proficiency. By working through various problems, you can strengthen your understanding, identify areas where you need improvement, and develop problem-solving strategies. These practice problems are designed to help you master key skills and ensure you’re well-prepared for more advanced topics.
Problem Set 1: Solving Linear Equations

- Problem 1: Solve the equation 3x + 5 = 20.
- Problem 2: Solve for y in the equation 2y – 4 = 10.
- Problem 3: Find the value of x in the equation 5(x – 2) = 25.
Problem Set 2: Graphing Functions
- Problem 1: Graph the linear equation y = 2x + 3 and identify the slope and y-intercept.
- Problem 2: Plot the equation y = -x – 1 and determine where the line intersects the x-axis.
- Problem 3: Create a table of values for the equation y = x + 4 and graph it.
Working through these exercises will enhance your ability to solve equations and graph functions with ease. As you practice, focus on understanding the steps involved and how they connect to the concepts you’ve learned. Regular practice will build your confidence and make these tasks more intuitive.
Exploring Real-World Algebra Applications
Mathematical concepts are not only relevant in the classroom but are also essential tools in solving practical problems encountered in daily life. Understanding how to apply mathematical principles to real-world scenarios can enhance your problem-solving skills and deepen your comprehension of abstract ideas. From budgeting to engineering, the ability to manipulate variables and equations plays a critical role in numerous fields.
For instance, professionals in construction and design use equations to calculate materials needed for projects. Financial planners apply formulas to track expenses, predict savings, and manage investments. Additionally, technology experts use mathematical models to optimize algorithms and data structures. By recognizing these connections, you can better appreciate how foundational concepts are employed in various industries.
As you explore these applications, keep in mind that mastering these techniques enhances both theoretical knowledge and practical skills, making it easier to tackle challenges in the real world.
Review of Key Formulas in Chapter 2
Mastering the essential formulas is crucial for solving mathematical problems effectively. These formulas are the building blocks that allow you to tackle various types of equations and apply them to real-world situations. Understanding their structure and how they are derived can simplify complex tasks and improve problem-solving speed.
In this section, we will review some of the most important formulas that you need to keep in mind. Below is a summary of key formulas and their uses:
- Linear Equation Formula: y = mx + b
This formula represents the equation of a straight line, where m is the slope and b is the y-intercept.
- Point-Slope Form: y – y₁ = m(x – x₁)
This formula helps express the equation of a line when you know a point on the line and the slope.
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a
Use this formula to solve quadratic equations where a, b, and c are the coefficients in the equation ax² + bx + c = 0.
- Distributive Property: a(b + c) = ab + ac
The distributive property allows you to multiply a number across a sum or difference.
Familiarizing yourself with these formulas and knowing when to apply them will significantly enhance your ability to solve mathematical problems with confidence and precision.
Additional Resources for Success
To excel in solving mathematical problems, it’s important to go beyond the basic lessons and utilize various tools and resources. These additional materials can enhance your understanding, reinforce key concepts, and provide more practice opportunities. Whether you’re seeking video tutorials, interactive exercises, or study groups, these resources can offer valuable support on your journey to mastering the material.
Online Tools and Websites
- Khan Academy: Offers free video tutorials and practice exercises for various topics.
- Wolfram Alpha: A computational engine that can help solve equations and explain solutions step-by-step.
- Desmos: A graphing calculator tool to visualize functions and equations interactively.
- Mathway: Provides step-by-step solutions to math problems and offers explanations for each step.
Books and Study Guides
- Practice Makes Perfect: This series provides practice problems with detailed solutions to reinforce learning.
- Math for Dummies: A beginner-friendly resource that breaks down complex topics into simple explanations.
- Shmoop: Offers comprehensive study guides and explanations, particularly for high school mathematics.
Utilizing these resources can significantly improve your comprehension and problem-solving skills. Combining practice, exploration, and expert insights will provide a well-rounded approach to mastering mathematical concepts.