
As you approach the final assessment of this course, it’s essential to consolidate your understanding of the key concepts covered throughout the year. This section is designed to help you review important topics and ensure you’re fully prepared for the test. By focusing on the critical areas, you can confidently approach each problem with the right strategies and methods.
The material spans various aspects of advanced mathematical principles, including problem-solving techniques, theoretical foundations, and practical applications. From analyzing shapes and figures to working with complex formulas, mastering these concepts is crucial for success. Each section highlights the most important skills and knowledge needed to tackle the most common types of questions you’ll face.
With the right preparation, you’ll be equipped to handle any challenge. Whether you’re revisiting previously covered material or enhancing your skills in specific areas, this guide offers a structured path to help you navigate the topics effectively. Strengthen your grasp of the subject and approach the assessment with confidence.
Mathematical Concepts and Problem-Solving Techniques
In this section, we focus on consolidating your knowledge of essential topics and providing solutions to the most commonly encountered questions. By examining key principles and applying them to different scenarios, you will strengthen your understanding and improve your problem-solving abilities. This guide is tailored to help you identify the critical areas that require attention and give you the tools to tackle each challenge effectively.
Understanding the foundational concepts is crucial for successfully completing the tasks ahead. Whether it’s working with shapes, analyzing relationships between different figures, or applying complex formulas, each skill plays a vital role in achieving mastery. The problems presented here have been selected to test your comprehension and ensure you’re ready for the final assessment.
To maximize your success, focus on breaking down each problem into manageable steps. Review key theorems and strategies, and practice solving problems methodically. With the right approach, you will build the confidence necessary to excel in the upcoming evaluation.
Key Concepts for Geometry Exam
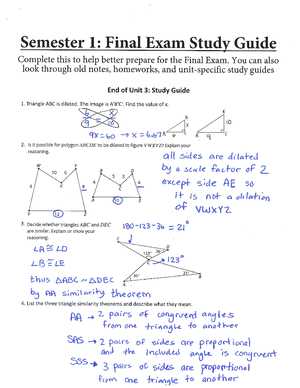
Mastering the essential ideas in this subject is the foundation of success. A clear understanding of the most important concepts will allow you to approach any problem with confidence. This section highlights the core topics that are essential for tackling various types of questions, focusing on how to apply fundamental principles to different scenarios.
Core Theorems and Postulates
Familiarizing yourself with key theorems and postulates will significantly enhance your problem-solving skills. These principles serve as the building blocks for many of the more complex tasks you will face. Understanding their applications is crucial for success in any type of question involving shapes, angles, and measurements.
| Theorem/Postulate | Description |
|---|---|
| Pythagorean Theorem | Describes the relationship between the sides of a right triangle: a² + b² = c². |
| Angle Sum Theorem | The sum of the angles in a triangle is always 180°. |
| Parallel Postulate | If two parallel lines are cut by a transversal, alternate interior angles are congruent. |
Essential Skills for Problem Solving
Alongside understanding the core concepts, honing your ability to solve problems efficiently is vital. Developing a systematic approach for breaking down each question allows you to stay focused and organized. Practice solving problems step by step, ensuring you understand how each concept fits into the overall solution.
Understanding Geometric Proofs
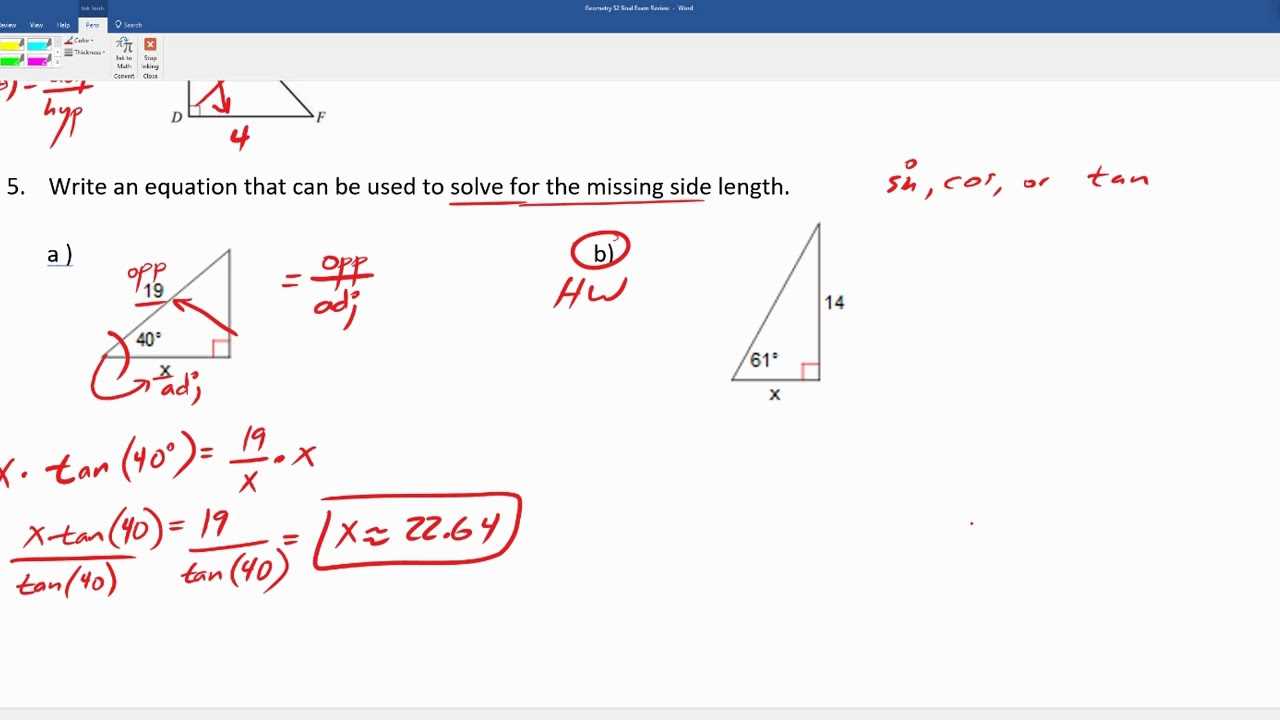
Being able to construct logical arguments and justify conclusions is a fundamental skill in mathematics. Proofs are essential for validating relationships between various elements in a figure, establishing connections between properties, and demonstrating the truth of statements. The key to mastering this skill is understanding the structure and reasoning behind each proof, which requires both practice and attention to detail.
When working through a proof, it’s important to break down each statement into smaller, more manageable parts. Each step should follow logically from the one before it, with every conclusion being supported by known theorems, postulates, or definitions. Developing a clear method for constructing proofs will improve both your understanding and confidence when solving more complex problems.
| Proof Type | Description |
|---|---|
| Two-Column Proof | A logical sequence where statements are listed in one column, and reasons for those statements in the second column. |
| Paragraph Proof | A more narrative form of proof where the reasoning is presented in a written paragraph format. |
| Flowchart Proof | A diagrammatic representation where steps are connected by arrows to show the logical flow of reasoning. |
Solving Triangle Congruence Problems
Understanding the relationships between the sides and angles of triangles is essential for solving many geometric problems. Congruence between two triangles means they are identical in size and shape, and recognizing this property is key when working with these figures. By applying specific criteria, you can determine when two triangles are congruent and use that information to solve a variety of problems.
To effectively approach triangle congruence problems, focus on the criteria that can be used to prove two triangles are congruent. These include side-angle-side (SAS), angle-side-angle (ASA), and side-side-side (SSS), among others. Mastery of these conditions allows you to make logical conclusions based on the information provided in a problem.
Practice with different types of triangle congruence will strengthen your ability to recognize patterns and apply the appropriate rules. Once you identify the correct congruence condition, solving for unknown sides or angles becomes straightforward, helping you confidently complete problems with precision.
Mastering Coordinate Geometry Techniques
Coordinate-based methods allow you to solve geometric problems by working directly with numerical values and positions on a grid. This approach involves using the x and y axes to represent points, lines, and other shapes, translating abstract concepts into a more tangible form. Mastering these techniques is crucial for solving a wide range of problems involving distances, slopes, and equations of lines.
One of the key skills is understanding how to calculate the distance between two points, which is fundamental when working with figures on a coordinate plane. Additionally, grasping how to determine the slope of a line, and the equation of that line, enables you to analyze and solve problems involving straight lines and their relationships with other geometric elements.
To build confidence, focus on practice problems that involve plotting points, finding midpoints, and determining equations of lines. By understanding how these elements work together, you can confidently apply coordinate geometry techniques to a variety of mathematical challenges.
Analyzing Quadrilaterals and Polygons
Understanding the properties and relationships of multi-sided figures is a key component in solving many problems. Polygons, including quadrilaterals, are characterized by their straight sides and angles. Each shape within this category has its own unique set of properties that define its structure and behavior. Analyzing these figures involves recognizing these properties and applying them to solve various problems.
For quadrilaterals, focus on understanding the different types, such as squares, rectangles, parallelograms, and trapezoids, each with its own set of angle and side length rules. By identifying the specific characteristics of a given shape, you can apply relevant formulas to calculate areas, perimeters, and other important properties. For more complex polygons, the key is to break down the shape into simpler components, using techniques such as triangulation or applying sum formulas for interior and exterior angles.
Practice with a variety of shapes and problems will help you become proficient in quickly identifying key properties and applying the right methods for analysis. This approach enables you to efficiently solve problems involving both simple and more complex multi-sided figures.
Working with Circles in Geometry
Circles play an important role in many geometric problems, as their properties can be applied to a wide range of scenarios. Understanding how to work with circles requires familiarity with their components and the relationships between these elements. The key is to know how to calculate distances, areas, and angles associated with a circle using the appropriate formulas and principles.
To work effectively with circles, focus on the following concepts:
- Radius and Diameter: The radius is the distance from the center to any point on the circle, while the diameter is twice the radius, extending across the circle through its center.
- Circumference: The perimeter of a circle can be found using the formula C = 2πr, where r is the radius.
- Area: The area of a circle is given by A = πr², where r is the radius.
In addition to these basic properties, there are several important relationships to consider when working with angles and arcs. For example, the central angle subtended by an arc is proportional to the length of the arc, and the angle inscribed in a semicircle is always a right angle.
When solving problems involving circles, it’s important to understand how to apply these concepts in combination with other geometric principles. This includes calculating angles, solving for unknown lengths, and using symmetry to simplify complex problems.
Solving Area and Perimeter Questions

Determining the area and perimeter of shapes is a fundamental skill in mathematics, as it allows you to quantify the size and boundaries of various figures. By understanding the basic formulas and applying them correctly, you can solve problems involving both simple and complex shapes. Whether you’re working with polygons, circles, or irregular figures, mastering these calculations is essential for tackling a wide range of problems.
When solving for area and perimeter, it’s important to identify the shape you’re dealing with and choose the correct formula. Here are some of the most common formulas you’ll need:
- Rectangle: Area = length × width, Perimeter = 2(length + width)
- Triangle: Area = 1/2 × base × height, Perimeter = sum of all sides
- Circle: Area = πr², Perimeter (Circumference) = 2πr
- Square: Area = side², Perimeter = 4 × side
For more complex shapes, such as polygons with many sides or irregular figures, you may need to break the shape into smaller, simpler components. Using the properties of these smaller components will help you calculate the total area and perimeter more easily. Additionally, sometimes it is necessary to apply the Pythagorean theorem to find missing side lengths or use trigonometry for more complex angles.
By practicing with different types of problems, you will become more efficient at identifying the appropriate methods for calculating the area and perimeter of various figures, ensuring you’re ready to tackle any question that comes your way.
Exploring Volume and Surface Area
Understanding how to calculate the volume and surface area of three-dimensional figures is essential for solving problems related to space and measurement. These concepts allow you to determine the amount of space an object occupies and the total area of its outer surface. Mastery of volume and surface area calculations is useful in a wide range of applications, from real-world scenarios to more complex mathematical problems.
When working with three-dimensional objects, it’s important to know the specific formulas for different shapes. Here are some of the most commonly used formulas:
- Rectangular Prism:
- Volume = length × width × height
- Surface Area = 2lw + 2lh + 2wh (where l = length, w = width, h = height)
- Sphere:
- Volume = (4/3)πr³
- Surface Area = 4πr²
- Cylinder:
- Volume = πr²h
- Surface Area = 2πr² + 2πrh
- Cone:
- Volume = (1/3)πr²h
- Surface Area = πr(r + l) (where l is the slant height)
For more complex shapes, it’s often helpful to break the object down into smaller components that can be easily measured. For example, when calculating the surface area of a composite figure, you may need to find the surface area of individual parts and then add them together. Similarly, when calculating volume, dividing the shape into simpler pieces can make the process more manageable.
By practicing these formulas and techniques, you’ll develop a deeper understanding of three-dimensional shapes, and you’ll be able to confidently solve problems involving volume and surface area.
Key Theorems and Postulates Review

Understanding the fundamental principles that govern geometric relationships is crucial for solving various problems. Theorems and postulates serve as the foundation for reasoning and proof in mathematics, providing the tools to draw conclusions about shapes, angles, and distances. Mastering these concepts is essential for tackling more advanced problems and deepening your understanding of geometric structures.
Important Theorems to Know
Several key theorems play a significant role in understanding the properties of geometric figures. Some of the most essential theorems include:
- Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This is expressed as a² + b² = c², where a and b are the legs, and c is the hypotenuse.
- Triangle Sum Theorem: The sum of the interior angles of any triangle is always 180°.
- Congruence Theorems: The conditions for triangles to be congruent include Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Angle-Angle-Side (AAS).
Essential Postulates for Proofs
Postulates are accepted truths that don’t require proof. They are the building blocks for geometric reasoning and proofs. Some key postulates include:
- Ruler Postulate: The distance between any two points on a line can be measured using a ruler, and the distance is always a non-negative real number.
- Segment Addition Postulate: If three points are collinear, the sum of the lengths of two smaller segments equals the length of the larger segment.
- Angle Addition Postulate: If two angles are adjacent, their sum is equal to the angle formed by the two non-overlapping parts.
By applying these theorems and postulates, you will be equipped to solve a variety of geometric problems. Understanding their applications and interrelationships is key to building a solid foundation in mathematical reasoning.
Angles and Parallel Lines Explained
Understanding the relationship between angles and parallel lines is fundamental to solving various geometric problems. When two straight lines are parallel, they never meet, and this property gives rise to several key angle relationships that are crucial for problem-solving. By recognizing these relationships, one can easily determine unknown angles and prove various geometric properties.
Parallel lines, when intersected by a transversal, create pairs of angles that have specific relationships. These relationships are useful in determining angle measures and proving geometric theorems. Here are some key angle relationships that arise when parallel lines are cut by a transversal:
- Corresponding Angles: Angles in the same relative position at each intersection are equal.
- Alternate Interior Angles: Angles on opposite sides of the transversal and inside the parallel lines are congruent.
- Alternate Exterior Angles: Angles on opposite sides of the transversal and outside the parallel lines are congruent.
- Consecutive Interior Angles: Angles on the same side of the transversal and inside the parallel lines are supplementary, meaning their sum is 180°.
These angle relationships form the basis for many theorems and proofs involving parallel lines. For example, the fact that corresponding angles are equal or consecutive interior angles are supplementary can help you establish congruence and similarity between shapes, or determine the value of unknown angles in a figure. Understanding these concepts is key to successfully solving geometric problems involving parallel lines and angles.
Geometric Transformations Simplified

In the study of shapes and their properties, transformations play a key role in understanding how figures change position, size, or orientation. These movements can be applied in various ways, each altering the figure in specific manners while maintaining certain characteristics. By mastering these transformations, one can predict the outcome of changes to geometric objects and solve complex problems more effectively.
There are several types of transformations that are commonly studied, each with its own set of rules and effects on the shape. The most fundamental types include:
- Translation: This involves shifting a figure from one location to another without altering its size, shape, or orientation. Every point in the figure moves the same distance in the same direction.
- Reflection: This transformation flips a figure over a line, creating a mirror image. The figure’s orientation changes, but its size and shape remain the same.
- Rotation: A figure is turned around a fixed point, usually the center of the figure. The rotation can occur by any degree, but the figure’s size and shape remain unchanged.
- Dilation: This transformation involves resizing a figure either by enlarging or reducing it. The shape maintains its proportions, but its size changes.
Understanding how these transformations work and how they affect the figure is crucial for solving many types of geometric problems. By applying these concepts, you can explore the symmetries of shapes, analyze properties, and solve problems involving congruence and similarity. Transformations offer a powerful method for manipulating geometric figures and revealing their underlying properties.
Reviewing Pythagorean Theorem Applications
The Pythagorean theorem is a fundamental concept used to solve a wide variety of problems involving right-angled triangles. This powerful tool allows us to relate the lengths of the sides of a right triangle and is essential in both theoretical and real-world problem-solving. By applying this principle, we can determine unknown side lengths or verify whether a triangle is a right triangle based on its side lengths.
One of the key applications of the theorem is in geometry, where it helps us solve problems related to distance, angles, and areas. In addition, the theorem is used in fields such as engineering, architecture, and physics, where precise measurements and calculations are crucial. Understanding how to apply this concept is critical for mastering various geometric principles and solving complex problems.
Using the Theorem to Find Missing Sides
The most common use of the Pythagorean theorem is to find the length of an unknown side in a right triangle. Given the lengths of two sides, you can calculate the third side using the formula:
a² + b² = c², where a and b are the lengths of the two legs, and c is the length of the hypotenuse.
Real-World Applications of the Theorem
The theorem extends beyond the classroom and is used in practical situations. For example, it is used to calculate distances between points in coordinate planes, to design structures, and even in navigation and computer graphics. Whether you’re calculating the shortest path between two points or determining the height of an object from a distance, the Pythagorean theorem is a reliable and essential tool.
Understanding Similarity and Ratios
In the study of shapes and their properties, similarity plays a crucial role in understanding how figures relate to one another. When two objects are similar, their shapes are the same, but their sizes may differ. The concept of similarity helps us recognize proportional relationships between corresponding parts of different figures, enabling us to solve problems involving measurements, scaling, and comparison.
At the heart of similarity lies the idea of ratios. A ratio expresses the relative size of two quantities and is a key concept in comparing the dimensions of similar objects. By examining corresponding sides, angles, and other measurements, we can determine how one figure compares to another in terms of scale and proportion.
Understanding the relationship between similarity and ratios allows us to solve a variety of practical problems. For example, scaling models, designing architectural blueprints, or calculating the size of objects from a distance all involve the use of proportional reasoning. Mastering this concept is essential for working with geometric figures and applying these ideas in real-world scenarios.
Coordinate Geometry and Distance Formula
In the study of shapes and space, coordinate systems provide a powerful framework for understanding the positioning of points and calculating distances between them. The distance formula is a fundamental tool used to measure the straight-line distance between two points on a plane. By applying this formula, we can determine the spatial relationships between points and solve problems involving distances and locations.
The formula is derived from the Pythagorean theorem and involves the use of the coordinates of two points. By finding the differences in the x and y coordinates of the points, we can calculate the distance between them. This is a crucial technique used not only in geometry but also in fields such as physics, engineering, and navigation.
Mastering the distance formula enables us to solve a variety of problems, such as determining the shortest path between two locations, calculating the length of a line segment, or even analyzing the geometry of complex shapes. Understanding how to apply this formula is essential for working in the coordinate plane and tackling real-world challenges involving spatial relationships.
Reviewing Geometric Constructions Techniques
Constructing precise shapes and figures is a key skill in the study of spatial relationships. The ability to create accurate representations of geometric objects relies on a set of techniques that allow you to manipulate tools like compasses, rulers, and protractors to create exact diagrams. These methods are essential for solving problems and understanding the properties of shapes in a practical, hands-on way.
In this section, we will explore various construction methods and how they can be applied to create points, lines, and angles. These techniques often form the foundation for more complex concepts and are used frequently in problem-solving scenarios. Mastery of these techniques will enhance your understanding of the underlying principles of shape creation and measurement.
Common Construction Methods
- Bisecting Angles: This technique involves dividing an angle into two equal parts using a compass and straightedge.
- Constructing Perpendicular Lines: By using the compass and ruler, perpendicular lines can be constructed from a given line at any point.
- Creating Parallel Lines: Parallel lines can be drawn by transferring a specific angle using the properties of corresponding angles.
Practical Applications of Constructions
- Finding the Circumcenter: Geometric construction is used to find the center of a triangle where all the perpendicular bisectors meet.
- Constructing Triangles: Using given lengths or angles, you can accurately construct triangles of different types, such as equilateral, isosceles, or scalene.
- Dividing Segments: A common technique for dividing a line segment into equal parts, useful in both basic constructions and more complex designs.
By practicing these techniques, you will not only develop a deeper understanding of geometric principles but also improve your ability to approach real-world challenges that require precision and attention to detail.
Practice Problems for Geometry Mastery

To truly master the concepts of shapes, figures, and their relationships, consistent practice is key. Working through a variety of problems not only reinforces what you have learned but also helps uncover areas where you might need additional focus. In this section, we will present several problems that challenge your understanding of key concepts and help build your problem-solving skills.
By engaging with these exercises, you’ll deepen your comprehension of core principles, such as spatial reasoning, measurement, and the relationships between different geometric elements. These problems will test your ability to apply formulas, theorems, and construction methods to real-world scenarios.
Practice Problems
- Problem 1: Calculate the area of a triangle given its base is 12 cm and height is 5 cm.
- Problem 2: A circle has a radius of 7 inches. Find its circumference and area. (Use π ≈ 3.14)
- Problem 3: Given a right triangle with legs of lengths 9 cm and 12 cm, determine the length of the hypotenuse.
- Problem 4: Construct an equilateral triangle with a side length of 8 cm. Explain the steps and the reasoning behind each step.
- Problem 5: A parallelogram has an area of 36 square units. If its base is 6 units, what is its height?
- Problem 6: Solve for x in the equation of similar triangles, where the corresponding sides are in the ratio 3:4 and the shorter side is 9 cm.
Attempting these problems will help solidify your understanding and enhance your ability to tackle more complex questions in the future. Remember to take your time, approach each problem step by step, and don’t hesitate to review any concepts if needed.
Final Tips for Geometry Exam Success

To achieve success in your assessment, it’s important to combine both solid preparation and effective test-taking strategies. With the right approach, you can confidently tackle the challenges ahead. Here are some final tips to help you make the most of your study time and perform at your best when it counts.
Effective Study Strategies
- Review Key Concepts: Focus on understanding the fundamental principles behind the problems, rather than just memorizing formulas. Mastery of core concepts will make solving unfamiliar problems easier.
- Practice Regularly: Consistent practice will help you identify your strengths and weaknesses. Work through a variety of problems, and pay attention to your mistakes so you can learn from them.
- Utilize Visual Aids: Drawing diagrams, using models, or visualizing the problem can make abstract concepts easier to grasp and help with problem-solving.
- Form Study Groups: Collaborating with peers can provide new perspectives on difficult topics. Explaining concepts to others also reinforces your own understanding.
Test-Taking Tips
- Read Instructions Carefully: Be sure to thoroughly read each question before starting. Understanding exactly what is being asked will save you time and prevent costly errors.
- Manage Your Time: Allocate time for each section based on the number of questions and difficulty. Don’t spend too much time on any single problem; move on and come back if necessary.
- Double-Check Your Work: If time allows, revisit your answers to ensure accuracy. Look for any mistakes, especially with calculations and key steps in problem-solving.
- Stay Calm: Stay focused and keep a positive mindset. If you come across a difficult problem, take a deep breath, skip it, and return to it later with a clear mind.
By applying these tips, you can approach your test with confidence and improve your chances of success. Remember, preparation and a calm, methodical approach are key to doing your best. Good luck!