
In this section, you’ll find valuable solutions and explanations for various exercises designed to enhance problem-solving abilities. Whether you’re revising previously covered material or tackling new concepts, this guide will offer clear steps to follow for each problem.
Understanding the methods and techniques provided here can make a significant difference in grasping the subject matter. The solutions not only show the correct answers but also provide insights into how to approach different types of problems, helping students develop a deeper understanding.
By reviewing the provided responses, learners can compare their work and identify areas where they might need further practice. This process is essential for mastering the topics and building a strong foundation for more advanced studies.
Go Math Chapter 6 Answer Key
This section provides detailed solutions and explanations for the exercises presented in the sixth unit. It is designed to guide students through the process of solving problems, ensuring they understand the logic behind each step and are able to apply similar methods in future tasks.
Step-by-Step Problem Breakdown
Each solution is broken down into clear, manageable steps. This approach helps students follow along and comprehend the reasoning behind the methods used. By analyzing these steps, learners can strengthen their problem-solving skills and gain a better understanding of how to approach different types of exercises.
How to Maximize Learning with Provided Solutions
Reviewing the solutions carefully allows students to compare their own work and identify areas for improvement. This process enhances retention and encourages a more analytical approach to solving future problems. The key to mastering these concepts lies in consistent practice and a deep understanding of the fundamental techniques demonstrated in the provided examples.
Overview of Go Math Chapter 6
This section focuses on a variety of key concepts that build a strong foundation for advanced topics. Students will explore essential techniques, sharpen their analytical skills, and learn to solve a range of problems effectively. By mastering the concepts covered here, learners gain the confidence to tackle more complex challenges in future studies.
Core Concepts and Techniques
The exercises in this section emphasize problem-solving strategies, covering both basic and more advanced methods. Each topic is introduced in a clear, logical sequence to help students understand the material step by step. The focus is on strengthening critical thinking and analytical skills that are vital for success in future lessons.
Importance of Practical Application
Applying the techniques learned in this section to real-world problems is crucial for mastering the material. By practicing with various examples, students can gain hands-on experience and improve their ability to solve similar problems independently. This practical approach ensures that learners can confidently use these methods outside of the classroom setting.
Key Concepts Covered in Chapter 6
This section introduces a variety of essential principles designed to enhance problem-solving abilities. The focus is on building a solid foundation through the exploration of fundamental techniques, which will help learners understand more complex material in later units. By the end of this unit, students should be equipped with a deeper comprehension of core topics that will serve them in future lessons.
Core Principles Explained
Throughout this section, the following concepts are explored in detail:
- Basic problem-solving techniques
- Strategies for approaching multi-step exercises
- Understanding numerical patterns and relationships
- Application of operations in diverse contexts
- Key rules for manipulating equations
Practical Approaches to Mastery
Students will engage with these core principles through a series of practice exercises that reinforce their understanding. The goal is to build confidence in applying these techniques to a wide range of problems, both in and out of the classroom.
How to Use the Answer Key Effectively
Utilizing a solutions guide is not just about finding the correct results; it’s about understanding the reasoning behind each step. This approach ensures that students learn how to solve problems independently and apply similar strategies to future tasks. The goal is to use the provided solutions as a learning tool rather than simply as a quick reference for answers.
Review Each Step Carefully
When using the solutions guide, it’s important to examine each step in the process. Focus on understanding why certain methods are applied and how different concepts interact. This will help solidify your grasp of the material and improve your problem-solving skills for future exercises.
Compare and Reflect on Your Work
After completing an exercise on your own, compare your solution with the one provided. Identify any differences in approach or calculation. This practice will highlight areas where you may need additional focus, helping you refine your techniques and increase your accuracy.
Common Mistakes in Go Math Chapter 6
When working through problems in this section, students often encounter several recurring challenges. These mistakes can hinder progress and prevent a full understanding of the material. Recognizing and addressing these errors early on is key to improving accuracy and building confidence in solving future problems.
One common issue is misinterpreting the instructions or failing to break down multi-step problems properly. Skipping steps or rushing through calculations often leads to incorrect results. Another frequent mistake involves overlooking the importance of proper sequencing when applying mathematical operations, which can cause errors in more complex exercises.
Additionally, confusion can arise from incorrectly applying formulas or mixing up similar concepts. This typically happens when students fail to fully understand the underlying principles behind each technique. By practicing with attention to detail, these issues can be minimized, leading to stronger problem-solving skills.
Step-by-Step Problem Solving Guide
This guide walks through the process of tackling problems systematically, ensuring that each step is understood and correctly executed. By following a clear sequence of actions, students can build confidence and accuracy when solving complex exercises. Each stage is designed to enhance comprehension and ensure that no important details are overlooked.
Breaking Down the Problem
The first step is to carefully read the problem and identify what is being asked. Pay attention to key details, such as numbers, operations, and any specific instructions. This clarity will help in determining the most effective approach to solving the problem.
Applying the Correct Method
Once the problem is understood, it’s crucial to choose the right method or formula. Depending on the task, this could involve using a specific rule or applying operations in a certain order. Double-check that each step follows logically from the previous one to avoid mistakes. Consistency in applying these techniques is key to achieving the correct result.
Understanding Key Formulas and Equations
Grasping the underlying principles of formulas and equations is essential for solving problems effectively. These tools provide structured ways to relate different variables and reach a solution. By mastering the core formulas in this section, students can confidently tackle more complex tasks and ensure accuracy in their calculations.
Core Formulas to Master
Here are some of the important formulas to focus on:
- Operations involving fractions and decimals
- Equations for solving unknown variables
- Rules for combining and simplifying terms
- Conversion formulas for measurement units
Applying Formulas to Real-World Problems
Once the formulas are understood, the next step is to apply them to practical problems. This involves recognizing which formula is most appropriate for each situation and correctly applying it to find the desired result. Repeated practice with these formulas will strengthen problem-solving skills and enhance understanding.
Practice Problems with Solutions
Working through practice problems is a critical step in reinforcing understanding and improving problem-solving abilities. This section presents several examples to work through, with clear solutions provided to guide you in mastering the material. These problems will help you identify common challenges and learn the correct approach to solving similar tasks.
Example Problems
Below are practice problems along with their solutions. Use these examples to test your understanding and check your results:
| Problem | Solution |
|---|---|
| 1. Solve for x: 5x + 3 = 18 | x = 3 |
| 2. Simplify: 3(4 + 2) | 18 |
| 3. Convert 3/4 to a decimal | 0.75 |
How to Solve Similar Problems
These problems serve as examples of the types of exercises you will encounter. Practice by attempting similar problems on your own, using the provided solutions to guide your steps. The more you practice, the more confident you’ll become in applying these methods to different types of problems.
How Teachers Can Utilize the Answer Key
For educators, the solutions guide is an invaluable resource to support effective teaching and help students master essential skills. It provides not only the correct results but also a structured approach to solving problems. Teachers can use it to assess students’ progress, identify common mistakes, and provide targeted guidance to reinforce key concepts.
One way teachers can benefit from this resource is by reviewing the solutions before the lesson to ensure they understand the method behind each problem. This allows for a more confident explanation during class and helps in providing students with clearer, more detailed feedback.
Classroom Benefits
Using the guide during lessons offers several advantages:
| Benefit | Description |
|---|---|
| Identify Mistakes | Helps teachers spot common errors students make, allowing for timely corrections. |
| Track Progress | Enables teachers to track students’ understanding and identify areas that need further review. |
| Provide Support | Equips teachers to offer targeted help where students struggle most. |
Enhancing Student Engagement
When used interactively, the solutions guide can also help keep students engaged. Teachers can present problems to the class, ask students to solve them, and then review the solutions together. This collaborative approach encourages participation and deepens comprehension.
Tips for Students to Improve Understanding
Mastering new concepts requires not only practice but also an active approach to learning. By incorporating effective study habits and focusing on key techniques, students can improve their understanding and enhance their problem-solving abilities. Here are some valuable strategies to help strengthen your grasp on the material.
Effective Study Strategies
Adopting the right study habits is essential for academic success. Below are some tips that can help improve your understanding:
- Review each problem step-by-step to ensure you fully understand the reasoning behind each solution.
- Practice regularly to reinforce your knowledge and identify areas that need more attention.
- Work with classmates or tutors to discuss difficult concepts and share different problem-solving strategies.
- Use supplementary resources, such as practice exercises and instructional videos, to deepen your understanding of challenging topics.
Engagement with Solutions
Engaging with provided solutions in an active way is also beneficial. Here’s how to make the most of solutions:
- After attempting a problem, compare your solution with the one provided and analyze any differences.
- Break down the steps in the solution to understand the reasoning behind each one.
- Use the solutions to identify common mistakes and learn how to avoid them in future problems.
Go Math Chapter 6 Review Questions
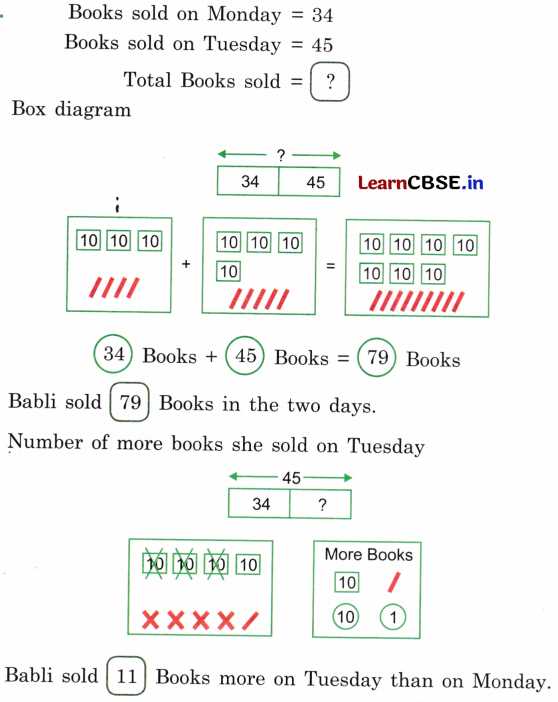
To reinforce your understanding and assess your progress, review questions are an excellent tool. These questions test your grasp of the key concepts, allowing you to practice applying the techniques you’ve learned. By working through these problems, you can identify areas of strength and areas that may require further study. Below are several review questions to help you solidify your knowledge.
Review Problems
Below is a set of review questions that cover the key concepts from this section. Attempt each one and check your understanding as you go:
| Problem | Solution |
|---|---|
| 1. Solve for x: 4x + 7 = 27 | x = 5 |
| 2. Simplify: 2(3 + 5) – 4 | 12 |
| 3. Convert 3/8 to a decimal | 0.375 |
| 4. What is the area of a rectangle with length 8 and width 5? | 40 |
| 5. Subtract: 15 – 9 | 6 |
These review questions are designed to test your understanding of the core skills. Work through them carefully, ensuring you understand each step before moving to the next problem.
Strategies for Completing Chapter 6 Exercises
Successfully completing exercises requires a combination of focus, understanding, and the right approach. By applying specific strategies, you can improve your problem-solving skills and work through tasks more efficiently. These methods will help you approach each problem with confidence and accuracy.
Effective Problem-Solving Techniques
Here are some strategies to enhance your approach to solving exercises:
- Understand the Problem: Before jumping into the solution, take a moment to read the problem carefully. Identify key information and what is being asked.
- Break It Down: Split the problem into smaller, more manageable parts. Tackle each part step by step instead of feeling overwhelmed by the entire problem.
- Work Through Examples: Review examples in your study materials to see how similar problems are solved. This can give you a clear idea of the process to follow.
- Use Visual Aids: Drawing diagrams, charts, or graphs can help clarify complex concepts and make abstract ideas easier to understand.
- Double-Check Your Work: After solving a problem, go back and verify your steps. This helps ensure no mistakes are overlooked.
Staying Focused and Organized
Maintaining focus and staying organized can improve your efficiency when completing exercises:
- Set a Timer: Work in focused intervals, such as 25-minute sessions, followed by short breaks. This helps maintain concentration without getting overwhelmed.
- Stay Organized: Keep your work space clean and organized. Arrange your materials and tools before starting to avoid distractions.
- Ask for Help When Needed: If a concept is unclear, don’t hesitate to ask for help. Whether it’s a teacher, tutor, or classmate, collaboration can help clarify difficult points.
By applying these strategies, you can tackle exercises with greater efficiency and improve your understanding of the material. Regular practice, combined with these techniques, will help you build confidence and master the concepts.
How Chapter 6 Builds Mathematical Skills
Section 6 is designed to progressively develop a variety of essential problem-solving abilities. By introducing new techniques and reinforcing previously learned concepts, it helps students enhance their understanding and application of core principles. This structured approach allows for the gradual acquisition of skills that are applicable to both simple and complex tasks.
The section focuses on strengthening key abilities that contribute to overall competency, such as recognizing patterns, applying formulas, and solving multi-step problems. Each exercise helps students practice these skills, solidifying their foundation for future learning.
Skill Development Through Practice
The various exercises in this section target specific competencies, encouraging improvement in different areas:
| Skill | Description | Application |
|---|---|---|
| Problem Solving | Breaking down complex problems into simpler steps. | Improves logical thinking and critical reasoning abilities. |
| Pattern Recognition | Identifying repeating elements and relationships within problems. | Helps predict outcomes and identify trends in future tasks. |
| Formula Application | Using mathematical rules and expressions to solve problems. | Strengthens understanding of how to manipulate variables and solve for unknowns. |
| Multi-Step Solutions | Integrating multiple steps to solve more complex problems. | Prepares students for advanced problem solving in various contexts. |
By consistently engaging with these exercises, students are able to refine these core skills, making them more adept at handling progressively complex tasks. The steady advancement through these techniques ensures that learners not only master the current material but also gain confidence in their ability to tackle new and challenging problems in the future.
Connection to Previous Go Math Chapters
The concepts introduced in this section build upon the foundational skills and techniques explored in earlier sections. Each topic is carefully designed to align with previous lessons, reinforcing and expanding on the knowledge students have already acquired. By making these connections, learners can see how their previous understanding is crucial for mastering more advanced topics.
This progression encourages a deeper comprehension of the subject matter, as each new idea is tied back to prior content, making it easier for students to see the relevance and application of what they’ve already learned. It helps bridge the gap between individual topics, creating a coherent learning experience that prepares students for future lessons.
How Earlier Topics Relate to Section 6
- Basic Operations: The skills of addition, subtraction, multiplication, and division are essential for solving more complex problems in this section.
- Understanding Variables: Previous lessons on variables and expressions provide a solid foundation for the more advanced manipulations found in this section.
- Patterns and Sequences: Earlier exercises on recognizing patterns help in identifying and applying more intricate sequences in later problems.
- Problem Solving Strategies: Techniques learned in earlier chapters for breaking down and solving multi-step problems are crucial for handling the more complex tasks introduced here.
Linking New Concepts to Earlier Skills
- The new formulas and methods introduced build on the basics of algebraic manipulation and arithmetic from prior sections.
- Learning to apply these strategies reinforces previously learned skills, creating stronger connections between ideas and enhancing overall understanding.
- By reviewing and using earlier concepts, students are better equipped to apply them to more advanced and diverse challenges in this section.
As students progress through this section, they will notice how each concept fits together with the broader picture, reinforcing the importance of mastering earlier material. This interconnected approach not only strengthens current knowledge but also sets the stage for even more advanced learning in subsequent sections.
Additional Resources for Chapter 6
To further enhance your understanding and practice of the concepts introduced, there are several helpful materials and tools available. These resources are designed to support learning and provide additional practice, helping you solidify key skills and clarify any uncertainties. Whether you need supplementary exercises, video tutorials, or interactive tools, these resources can guide you through the learning process and deepen your comprehension.
Online Tools and Websites
- Interactive Learning Platforms: Websites like Khan Academy and IXL provide interactive exercises and detailed explanations on topics covered in this section. These platforms help reinforce concepts with step-by-step guidance and practice problems.
- Educational YouTube Channels: Channels such as Math Antics and PatrickJMT offer video tutorials that explain complex topics in a simple and easy-to-understand manner. These videos can be a great visual aid for understanding tricky concepts.
- Online Forums and Communities: Participating in discussion forums like Stack Exchange or Reddit’s learning communities allows you to ask questions, exchange tips, and collaborate with others who are also working through the same material.
Books and Study Guides
- Study Guides: Comprehensive guides such as those from the “For Dummies” series or Barron’s provide detailed explanations and examples of key topics. These books are designed to break down complex subjects into manageable sections, with exercises and solutions to help reinforce learning.
- Workbooks: Practice workbooks tailored to the current learning topic provide additional problems to solve, offering valuable practice to master the concepts covered.
- Teacher and Tutor Support: Many educators offer extra materials such as worksheets, practice tests, and additional resources that align with the curriculum. Reaching out for one-on-one help can clarify doubts and solidify understanding.
Using these additional materials can make a significant difference in your mastery of the topic. By supplementing the textbook with these resources, you can ensure that you are well-prepared for tests, assignments, and future lessons.
How to Prepare for Chapter 6 Tests
Preparing for a test involves more than just reviewing the material; it’s about understanding key concepts, practicing problems, and developing strategies to perform well under time constraints. The best approach combines a thorough review with focused practice on areas where you need improvement. In this section, we’ll explore effective ways to prepare for assessments related to the topics in this unit, ensuring you feel confident and ready when exam day arrives.
Effective Study Strategies
- Review Key Concepts: Go through your notes and textbooks to make sure you understand the foundational principles. Identify any areas that feel unclear and focus your efforts on these concepts.
- Practice with Problems: Solve problems from each section, especially those you find challenging. This will help reinforce your understanding and highlight areas that need more attention.
- Create Summary Sheets: Summarize important formulas, methods, and strategies in a concise sheet. This will serve as a quick reference guide during your revision and can also help with memory recall during the test.
Test-Taking Techniques
- Time Management: Practice solving problems under timed conditions. This helps you gauge how much time to spend on each question and ensures you don’t run out of time during the exam.
- Identify Question Types: Familiarize yourself with the types of questions that are likely to appear on the test. Knowing what to expect allows you to approach each question more confidently.
- Stay Calm and Focused: During the test, stay calm and read each question carefully. Don’t rush through the problems–taking a moment to think can save you time in the long run and prevent careless mistakes.
By following these strategies, you can effectively prepare for the upcoming test. Consistent practice and a clear understanding of the material are key to achieving success and feeling confident during the exam.
Benefits of Mastering Chapter 6 Content
Mastering the content covered in this unit offers numerous advantages, both in academic achievement and in the development of essential skills that can be applied beyond the classroom. A deep understanding of the material enables students to approach more complex topics with confidence and efficiency. By building a solid foundation in this section, learners are better prepared for future challenges, whether in exams or practical applications.
Enhanced Problem-Solving Skills
- Critical Thinking: Understanding the core concepts enables students to analyze and break down problems more effectively, leading to better decision-making.
- Logical Reasoning: With practice, students develop the ability to recognize patterns and use logic to solve problems, a skill valuable in many areas of life.
- Increased Efficiency: Mastery of key methods helps students solve problems faster and with fewer errors, saving time and reducing frustration during tests.
Stronger Academic Performance
- Improved Test Scores: A firm grasp of the material directly translates to better performance in assessments, boosting overall grades.
- Confidence Boost: When students feel confident in their understanding, they are more likely to engage actively in class discussions and participate in problem-solving exercises.
- Better Retention: Mastery of the material leads to longer-term retention, allowing students to apply their knowledge in future lessons and real-life situations.
By thoroughly mastering the content in this section, students not only improve their academic standing but also develop essential skills that will benefit them in many areas of their education and life. The effort put into understanding these concepts pays off in the form of increased success and greater confidence in tackling new challenges.