
As students approach the end of their coursework, a comprehensive review becomes essential for mastering key concepts. This guide is designed to help individuals confidently navigate the challenges of their upcoming evaluation, offering a clear path for preparation. Whether tackling equations, understanding graphs, or solving real-world problems, readiness is the key to success.
Focused practice can make all the difference, ensuring that each topic is not only understood but applied effectively. Throughout this section, we will explore the most important mathematical topics, offering both theoretical insight and practical exercises to reinforce learning. Mastery of these core areas will boost your confidence and allow you to tackle any problem that may appear.
We will also provide useful strategies for managing time and minimizing stress during the assessment. Proper preparation is not just about knowing the material, but also about approaching the test with the right mindset and tools. Let’s begin the journey toward mastering these essential mathematical concepts.
Algebra 1 Final Exam Preparation 2025
Preparing for an important mathematical assessment requires focused effort and a strategic approach. This section aims to guide you through the necessary steps to ensure you are fully ready. By reviewing key concepts, practicing problem-solving techniques, and learning to apply your knowledge efficiently, you can approach the test with confidence.
First, it’s essential to refresh your understanding of the core principles you’ve learned throughout the course. From simplifying expressions to solving complex equations, mastering these fundamental skills will provide a strong foundation for tackling any challenge. Consistent practice and active engagement with the material are critical components in strengthening your problem-solving abilities.
Additionally, being familiar with the structure and types of questions typically asked will help reduce uncertainty. The more you understand the format, the better you can manage your time and approach each section systematically. Developing a review schedule, allowing ample time for both revision and practice tests, will maximize your preparation.
Overview of Algebra 1 Exam Structure
Understanding the structure of the upcoming assessment is crucial for effective preparation. By familiarizing yourself with the different sections, types of questions, and time limits, you can approach the test with confidence and focus. The format is designed to evaluate your grasp of core mathematical concepts and your ability to apply them to solve various problems.
Types of Questions and Content Areas
The evaluation typically includes a variety of question types, such as multiple choice, short answer, and word problems. Each section is aimed at assessing your proficiency in different mathematical skills, from basic calculations to more complex reasoning. Expect questions on equations, inequalities, and functions, among others. Being prepared for diverse question formats will help you stay organized and efficient during the assessment.
Time Management and Organization
Effective time management is vital for completing the assessment within the allotted time. It’s important to practice pacing yourself during mock tests to ensure you can answer all questions without rushing. Allocating time wisely across different sections will help you remain calm and focused, increasing your chances of success.
Key Topics Covered in Algebra 1
Throughout the course, various essential mathematical concepts are introduced and developed, all of which play a vital role in solving problems and understanding more advanced topics. These foundational skills are crucial for success in any mathematical evaluation and provide a basis for future learning. By mastering these areas, you will be well-equipped to tackle any questions that arise.
Understanding Equations and Inequalities
One of the core areas covered is the solving and manipulation of different types of equations and inequalities. This includes linear equations, systems of equations, and simple inequalities. Being able to solve for unknowns and interpret the solutions in a real-world context is essential for progressing in mathematics.
Functions and Graphing Techniques
Another critical topic is the study of functions and their graphical representations. Understanding how to graph linear and quadratic functions, as well as identifying key features like slopes and intercepts, is fundamental. Mastering this topic will help you solve problems more efficiently and visualize mathematical relationships.
Understanding Equations and Inequalities
At the heart of many mathematical problems are equations and inequalities. These structures help define relationships between different variables and form the foundation for more complex problem-solving. Mastery of these concepts is essential, as they are frequently tested and used in various real-life applications, from budgeting to engineering.
Solving Linear Equations
Linear equations represent the simplest form of equations. Solving them involves isolating the unknown variable on one side of the equation. The key steps typically involve simplifying both sides, combining like terms, and applying inverse operations. Below is an example of a basic linear equation and its solution steps:
| Step | Equation | Explanation |
|---|---|---|
| 1 | 2x + 5 = 15 | Start with the given equation. |
| 2 | 2x = 10 | Subtract 5 from both sides. |
| 3 | x = 5 | Divide both sides by 2 to solve for x. |
Working with Inequalities
Inequalities are similar to equations but involve a range of possible solutions. Rather than providing a single value, inequalities define a set of values that satisfy the condition. The process of solving them is much like solving equations, but with extra attention given to how the inequality symbol changes when multiplying or dividing by negative numbers. Here’s an example:
| Step | Inequality | Explanation |
|---|---|---|
| 1 | -3x ≥ 9 | Start with the given inequality. |
| 2 | x ≤ -3 | Divide both sides by -3 (flip the inequality symbol). |
By understanding these basic principles, you’ll be well-prepared to tackle more complex equations and inequalities encountered in the assessment.
Mastering Linear Functions and Graphs
Linear functions are among the most fundamental concepts in mathematics, representing relationships where variables change at a constant rate. Understanding how to work with these functions is essential for solving a variety of problems, both in academic contexts and in real-life applications. Once you are comfortable with linear functions, graphing them becomes a powerful tool to visually interpret data and relationships.
Understanding Slope and Intercept
One of the key features of linear functions is their slope and y-intercept. The slope represents the rate of change, or how much one variable increases or decreases in relation to another. The y-intercept is the point where the line crosses the vertical axis. These two elements are crucial when writing the equation of a line in slope-intercept form: y = mx + b, where m is the slope and b is the y-intercept.
Graphing Linear Functions
Graphing a linear function involves plotting two key points and drawing a straight line through them. To graph a line, start by plotting the y-intercept, then use the slope to find another point. For example, if the slope is 2, this means for every 1 unit you move to the right along the x-axis, you move up 2 units along the y-axis. This process can be repeated to draw the line accurately. Once the line is drawn, it represents all the possible solutions to the function.
Exploring Systems of Equations
Systems of equations involve solving multiple equations simultaneously, where the goal is to find the values of variables that satisfy all equations in the system. These types of problems are useful for modeling real-world situations where multiple conditions need to be met at once. Understanding how to solve these systems efficiently is a key skill in solving complex problems.
Methods for Solving Systems
There are several methods for solving systems of equations, each suited for different types of problems. The most common approaches include:
- Graphing: This involves plotting both equations on the same coordinate plane and finding the point where the lines intersect. The coordinates of this point are the solution to the system.
- Substitution: In this method, one equation is solved for one variable, and the result is substituted into the other equation to find the other variable.
- Elimination: This technique involves adding or subtracting the equations to eliminate one variable, making it easier to solve for the other.
Solving by Substitution Example
Consider the following system:
- 2x + 3y = 10
- 4x – y = 7
To solve by substitution, solve the second equation for y:
4x – y = 7 → y = 4x – 7
Now substitute this expression for y into the first equation:
- 2x + 3(4x – 7) = 10
- 2x + 12x – 21 = 10
- 14x = 31
- x = 31/14
Finally, substitute the value of x back into the equation for y to find the solution for y.
Polynomials and Their Operations Explained
Polynomials are a key component in many areas of mathematics, consisting of terms that involve variables raised to different powers. These expressions are central to solving a variety of problems, from simplifying equations to understanding complex relationships between variables. Understanding how to manipulate and operate with polynomials is essential for progressing in more advanced topics.
Basic Operations with Polynomials
There are several fundamental operations that can be performed on polynomials, including addition, subtraction, multiplication, and division. Each operation requires following specific rules to combine or simplify terms effectively.
- Addition and Subtraction: To add or subtract polynomials, simply combine like terms–terms with the same degree and variable. For example, (3x² + 2x) + (4x² – x) becomes 7x² + x.
- Multiplication: When multiplying polynomials, use the distributive property (also known as the FOIL method for binomials) to multiply each term in one polynomial by every term in the other. For example, (x + 3)(x + 2) results in x² + 5x + 6.
- Division: Polynomial division can be done using long division or synthetic division. This process is useful for breaking down more complex expressions into simpler forms.
Factoring Polynomials
Factoring polynomials is another essential operation. It involves rewriting a polynomial as a product of simpler polynomials. This is especially useful for solving equations or simplifying expressions. Common factoring techniques include:
- Factoring by grouping: Group terms in pairs to factor out the greatest common factor (GCF) from each pair.
- Factoring trinomials: Factor quadratic expressions into binomials, such as x² + 5x + 6 being factored as (x + 2)(x + 3).
Factoring Techniques for Algebra 1
Factoring is a powerful tool in simplifying and solving equations. By expressing a polynomial as a product of simpler polynomials, one can uncover solutions more easily and make complex problems more manageable. There are various methods for factoring expressions, each suited for different types of problems.
Common Factoring Methods
There are several key methods used in factoring polynomials, each designed for specific types of expressions:
- Factoring by Grouping: This method works when an expression has four terms. The idea is to group terms in pairs and factor out the greatest common factor (GCF) from each group. If done correctly, this should result in two binomials that can be factored further.
- Factoring Trinomials: Trinomials of the form ax² + bx + c can be factored into two binomials. This is done by finding two numbers that multiply to give ac and add up to b. For example, x² + 5x + 6 factors to (x + 2)(x + 3).
- Difference of Squares: This technique applies to expressions like a² – b². The result is a simple factorization of (a + b)(a – b). For example, x² – 9 factors to (x + 3)(x – 3).
- Perfect Square Trinomials: When a trinomial is a perfect square, such as x² + 6x + 9, it factors into a binomial squared: (x + 3)².
Step-by-Step Factoring Process
To effectively factor a polynomial, follow these general steps:
- Look for a common factor: Always check if there is a greatest common factor (GCF) that can be factored out from all terms before proceeding with other methods.
- Choose the appropriate method: Depending on the number of terms and the structure of the polynomial, select the most suitable factoring method, such as grouping or factoring trinomials.
- Check your factorization: After factoring, multiply the factors to ensure that you arrive back at the original expression. This helps verify your solution.
Simplifying Rational Expressions and Equations
Rational expressions and equations involve fractions that contain polynomials in the numerator and denominator. Simplifying these expressions is an important skill that makes complex equations more manageable. By reducing these fractions, we can make it easier to solve problems or perform operations like addition, subtraction, and multiplication.
Steps for Simplifying Rational Expressions
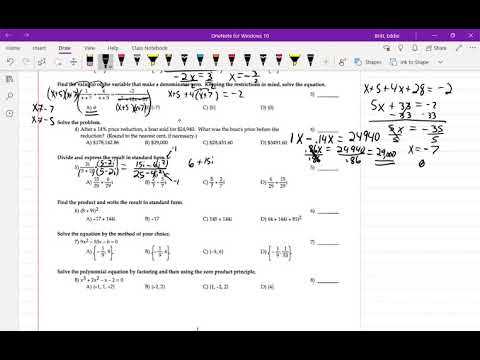
Simplifying a rational expression involves reducing it to its lowest terms. Here are the key steps:
- Factor the numerator and denominator: Look for common factors in both the top and bottom parts of the fraction. Factoring both parts helps in identifying and canceling out common terms.
- Cancel out common factors: Once the numerator and denominator are factored, cancel out any common factors. This is the key to simplifying the expression.
- Rewrite the expression: After canceling, write the simplified expression, ensuring there are no further common factors.
Example of Simplifying a Rational Expression
Consider the rational expression:
- (x² – 9) / (x² – 6x + 9)
First, factor both the numerator and the denominator:
- Numerator: x² – 9 is a difference of squares, so it factors to (x + 3)(x – 3).
- Denominator: x² – 6x + 9 is a perfect square trinomial, so it factors to (x – 3)(x – 3).
Now, the expression becomes:
- (x + 3)(x – 3) / (x – 3)(x – 3)
Cancel the common (x – 3) terms, leaving:
- (x + 3) / (x – 3)
This is the simplified form of the expression.
Solving Quadratic Equations Effectively
Solving quadratic equations is a fundamental skill in mathematics. These equations often appear in various real-world applications, and mastering efficient methods for solving them is crucial. There are several strategies available, each suited to different forms of the equation, allowing for quicker and more accurate solutions.
Common Methods for Solving Quadratic Equations
To solve these equations, the following methods are most commonly used:
- Factoring: This method involves rewriting the quadratic as a product of two binomials. If the equation can be factored, it simplifies the process significantly. For example, x² – 5x + 6 factors to (x – 2)(x – 3).
- Quadratic Formula: The quadratic formula is a universal tool that can solve any quadratic equation. Given a quadratic equation of the form ax² + bx + c = 0, the solution is found using the formula:
x = (-b ± √(b² - 4ac)) / 2aUse this formula when factoring is difficult or not possible. It provides the roots of the equation directly.
Step-by-Step Process for Solving by Factoring
When factoring is the method of choice, follow these steps:
- Write the equation in standard form: Ensure the equation is in the form of ax² + bx + c = 0.
- Factor the quadratic expression: Look for two numbers that multiply to give the product of ac and add up to b.
- Set each factor equal to zero: After factoring, set each binomial equal to zero and solve for the variable. For example, from (x – 2)(x – 3) = 0, solve for x to get x = 2 and x = 3.
By following these steps, you can quickly solve quadratic equations when factoring is possible, providing the solutions needed for a variety of problems.
Working with Exponents and Powers
Understanding how to manipulate exponents and powers is essential for solving many types of equations. These concepts allow us to express repeated multiplication in a compact form and simplify complex calculations. Mastery of the rules governing exponents makes it easier to work with large numbers and expressions in a variety of mathematical contexts.
Key Rules for Exponents
There are several fundamental rules that govern operations with exponents:
- Product Rule: When multiplying expressions with the same base, add the exponents. For example, x⁴ × x² = x⁶.
- Quotient Rule: When dividing expressions with the same base, subtract the exponents. For instance, x⁶ ÷ x² = x⁴.
- Power of a Power Rule: When raising a power to another power, multiply the exponents. For example, (x²)³ = x⁶.
- Power of a Product Rule: When raising a product to a power, apply the exponent to both terms in the product. For example, (xy)² = x²y².
- Negative Exponent Rule: A negative exponent represents the reciprocal of the base raised to the positive exponent. For instance, x⁻² = 1/x².
Examples of Simplifying Expressions
Here are some examples that demonstrate how to simplify expressions using the above rules:
- Example 1: Simplify x³ × x⁴. Using the product rule, add the exponents: x³ × x⁴ = x⁷.
- Example 2: Simplify y⁶ ÷ y³. Using the quotient rule, subtract the exponents: y⁶ ÷ y³ = y³.
- Example 3: Simplify (a²)⁴. Using the power of a power rule, multiply the exponents: (a²)⁴ = a⁸.
- Example 4: Simplify (3x)². Using the power of a product rule, apply the exponent to both terms: (3x)² = 9x².
By practicing these rules and applying them consistently, solving equations involving exponents becomes much easier and more intuitive.
Analyzing Word Problems in Algebra
Word problems are a common challenge in mathematical problem-solving. These problems require translating a written scenario into a mathematical equation or set of equations. The key to solving these problems is carefully identifying the relevant information, recognizing the mathematical relationships between quantities, and formulating a solution strategy.
To approach word problems effectively, start by breaking down the problem into smaller, manageable parts. Identify the knowns and unknowns, and determine how they are related. Once the structure is clear, set up an equation that reflects these relationships. Solving the equation will lead to the desired answer, which can then be interpreted in the context of the original problem.
Additionally, it’s important to pay attention to keywords and phrases that indicate specific operations. For example, words like “sum” or “total” suggest addition, while “difference” or “less” point to subtraction. By becoming familiar with these cues, solving word problems becomes a more systematic process.
Practicing different types of word problems helps to sharpen your skills in problem identification, equation formulation, and solution interpretation. With time, this process becomes more intuitive, allowing for quicker and more accurate solutions to a wide range of mathematical challenges.
Graphing Parabolas and Other Functions
Graphing functions is a key skill in mathematics, and understanding how to plot various types of curves, such as parabolas, is essential for visualizing mathematical relationships. The process of graphing involves translating an equation into a visual representation on a coordinate plane, helping to identify patterns, roots, and key features of the function. One of the most important types of graphs to master is the parabola, which often appears in quadratic equations.
To graph a parabola, first recognize its general form, typically written as y = ax² + bx + c. The shape of the parabola is determined by the value of a, which affects the width and direction of the curve. The vertex of the parabola, which represents either its highest or lowest point, can be found using specific formulas. From there, you can plot points and sketch the curve.
Key Steps for Graphing Functions
- Identify the type of function and its characteristics (e.g., whether it’s linear, quadratic, etc.).
- Find the vertex and other key points such as intercepts or asymptotes.
- Plot the points on the coordinate plane and connect them smoothly to form the graph.
- Analyze the graph for symmetry, direction, and key behaviors such as increasing or decreasing intervals.
Other Common Functions
In addition to parabolas, there are various other functions that require graphing, such as linear, exponential, and rational functions. Each function has its own set of characteristics, and understanding how to identify these is crucial for effective graphing. For instance, linear functions result in straight lines, while exponential functions have rapid growth or decay patterns. Understanding the unique properties of these functions allows for more accurate and efficient graphing.
Mastering the art of graphing enables you to not only visualize solutions to equations but also gain deeper insights into the behavior of mathematical functions. Practice with various types of equations will increase your confidence and proficiency in this important skill.
Using the Quadratic Formula Correctly
The quadratic formula is a powerful tool used to solve equations that involve second-degree terms. It provides a straightforward method for finding the roots or solutions of a given equation, especially when other methods like factoring are difficult or impossible to apply. Understanding how to correctly apply the quadratic formula can significantly simplify the process of solving such equations.
The general form of the quadratic equation is ax² + bx + c = 0. The quadratic formula is given as:
x = (-b ± √(b² – 4ac)) / 2a
Each component of the formula corresponds to a specific part of the equation. The values of a, b, and c are the coefficients from the quadratic equation. The discriminant, represented by b² – 4ac, plays a key role in determining the nature of the solutions. If the discriminant is positive, there will be two real solutions. If it is zero, there will be exactly one real solution, and if it is negative, the solutions will be complex or imaginary.
Steps for Using the Quadratic Formula
- Write the equation in the standard form ax² + bx + c = 0.
- Identify the values of a, b, and c.
- Substitute these values into the quadratic formula.
- Calculate the discriminant (b² – 4ac) and evaluate the square root.
- Apply the plus and minus sign in the formula to find the two possible values for x.
- Simplify the expression to get the final solutions.
Example Calculation
| Equation | Solution Steps | Result |
|---|---|---|
| x² – 5x + 6 = 0 |
|
x = 3 or x = 2 |
Mastering the quadratic formula allows for quick and accurate solutions to second-degree equations, especially when other methods are not feasible. Practice using the formula with various types of equations to build confidence in your problem-solving abilities.
Practice Questions for Exam Success
Practicing a variety of problems is crucial for mastering key concepts and ensuring confidence when tackling challenges. Engaging with a wide range of questions helps reinforce understanding, identify patterns, and improve problem-solving speed. By working through different types of problems, students can develop strategies for approaching unfamiliar situations and strengthen their skills.
Question Set 1: Solving Equations

Try solving the following problems to sharpen your skills in equation manipulation:
| Problem | Solution Method |
|---|---|
| 2x + 5 = 15 | Solve for x by isolating the variable. |
| 3(x – 4) = 12 | Expand the equation and solve for x. |
| 4x² – 9 = 0 | Factor the quadratic expression and solve for x. |
Question Set 2: Word Problems
Next, tackle these word problems to improve your ability to translate real-life situations into mathematical expressions:
| Problem | Solution Method |
|---|---|
| A store sells pencils at $0.50 each. How many pencils can you buy for $5? | Set up an equation and solve for the number of pencils. |
| The sum of two numbers is 30, and their difference is 10. What are the numbers? | Write a system of equations and solve for both numbers. |
| A car travels 60 miles per hour. How long will it take to travel 180 miles? | Use the formula: distance = rate × time. Solve for time. |
Regular practice with these types of questions will prepare you to handle similar problems under exam conditions. Don’t rush through the problems–focus on understanding each step, and soon you’ll find yourself more comfortable solving even the most challenging questions.
Tips for Time Management on Exam Day
Effective time management is essential to performing well under pressure. With limited time available during an assessment, it’s important to organize your approach and allocate your time wisely. By practicing efficient time management techniques, you can reduce stress, avoid rushing, and ensure you have enough time to tackle all sections of the test.
Prioritize and Plan
Start by quickly scanning the entire test to get an overview of the questions. Identify any sections that may require more time and allocate accordingly. If you are unsure about a question, it’s often best to move on and come back to it later. This strategy ensures that you don’t get stuck and waste precious time.
Stick to a Pace
One of the most effective strategies is to set time limits for each section. For example, if there are 50 questions and you have 90 minutes, aim to spend no more than 1-2 minutes per question. This keeps you from spending too much time on difficult questions and helps maintain a steady pace.
- Set mini-goals: For example, aim to finish 10 questions in 20 minutes.
- Keep track of time: Use a watch or timer to stay on track.
- Don’t dwell on one question: If stuck, mark it and move on to the next.
By practicing these time management tips, you’ll improve your ability to navigate the test efficiently, leading to a calmer and more successful experience. Remember that preparation is key–not only in mastering the material but also in mastering the clock.
How to Review Answers and Check Work
Reviewing your work is an essential part of ensuring accuracy and avoiding mistakes. After completing a test or task, taking the time to carefully check your answers can make a significant difference in your overall performance. By following a systematic approach, you can catch errors, improve your results, and gain confidence in your work.
Take a Systematic Approach
Begin by reviewing each question one at a time. Don’t just skim over the answers; read each question again thoroughly to ensure you understand what was asked. Then, compare your solution step-by-step with the correct method. Double-check that you’ve followed the proper procedures for each type of problem. This process helps to identify any missteps or oversights that could have occurred while working under time pressure.
Check for Common Mistakes
After reviewing each problem, look for common errors such as:
- Sign mistakes: Ensure that positive and negative signs are correctly placed, especially when dealing with subtraction and multiplication.
- Misplaced decimal points: These can lead to large errors in calculations.
- Incorrect formulas: Verify that you’ve applied the correct formula for each specific problem.
- Calculation errors: Recheck the arithmetic to ensure no simple mistakes were made.
By following these techniques and staying organized during the review process, you increase your chances of catching avoidable mistakes and improving your final results. A careful review can be the key to boosting your confidence and achieving success.