
When tackling challenging topics in mathematics, it’s crucial to grasp the underlying principles that shape the problems and solutions. This section will help clarify the most important techniques, offering guidance on how to approach tasks with confidence. Whether you’re dealing with complex equations or multi-step problems, understanding the foundational concepts will enhance your ability to solve them effectively.
Improving your skills involves a combination of practice and applying the right strategies. By breaking down each problem step by step, you’ll be able to identify patterns and methods that lead to accurate results. This approach not only strengthens your ability to handle similar challenges in the future but also builds the critical thinking necessary for mastering more advanced topics.
Common Core Lesson 19 Homework Overview
This section provides an in-depth look at the key topics and problem-solving techniques you’ll encounter in the current set of exercises. Focusing on essential mathematical concepts, the goal is to guide you through various types of questions, helping you build a strong foundation for more advanced topics in the subject. You will be introduced to several strategies that simplify complex problems and allow for more effective solutions.
Key Topics and Approaches
In this section, you will explore a range of topics that are central to the current set of tasks. These include basic arithmetic operations, algebraic manipulation, and problem-solving strategies. Each task requires understanding both the theory and the application of mathematical rules, enabling you to apply your knowledge to a variety of problem types.
Step-by-Step Problem Breakdown
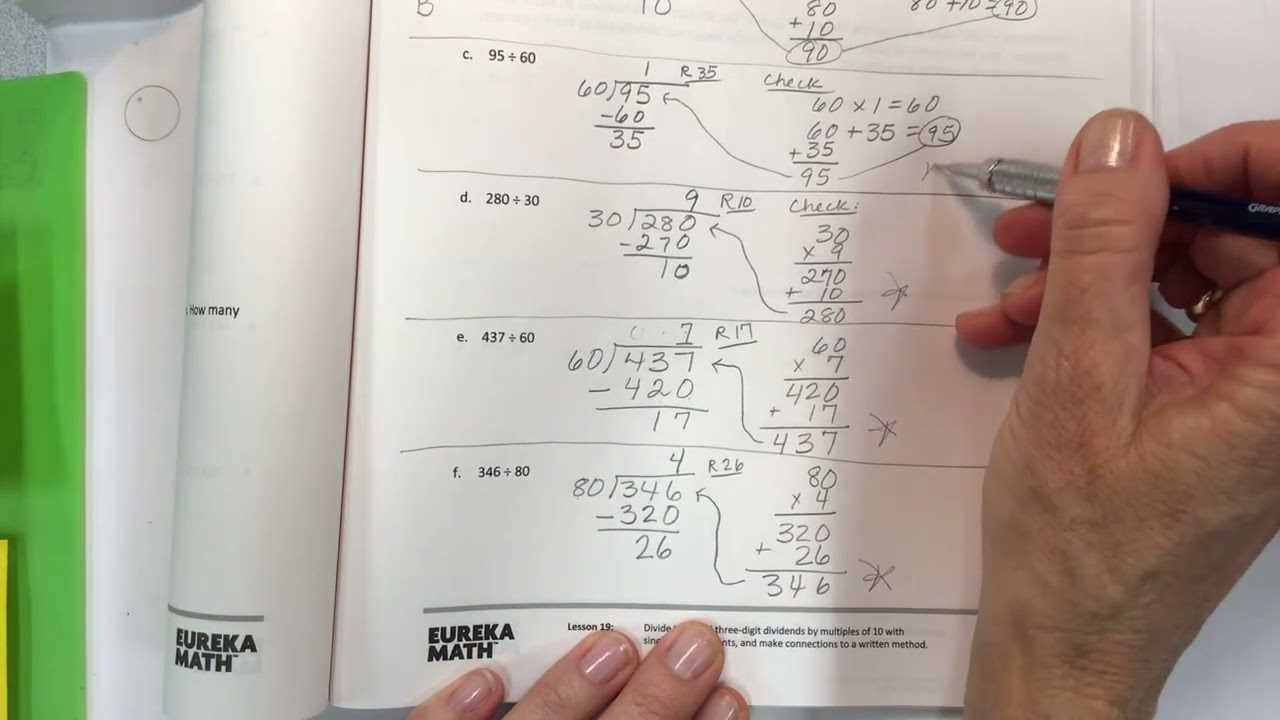
Breaking down each problem into smaller steps is essential for finding the correct solutions. This method helps identify patterns and possible shortcuts, making complex tasks easier to manage. By following the step-by-step approach outlined here, you will increase your ability to solve questions accurately and efficiently.
| Topic | Focus Area | Common Challenges |
|---|---|---|
| Arithmetic Operations | Basic addition, subtraction, multiplication, and division | Difficulty in handling large numbers and multi-step operations |
| Algebra | Solving equations and simplifying expressions | Understanding variable manipulation and balancing equations |
| Word Problems | Applying math to real-life scenarios | Extracting the right information and setting up equations |
Key Concepts Covered in Lesson 19
This section focuses on the essential principles and strategies that are vital for mastering the current set of tasks. Understanding these core topics will allow you to confidently tackle various mathematical challenges, ensuring both accuracy and efficiency in problem-solving. The concepts presented here will build the foundation for more complex tasks in the future.
Main Ideas and Techniques
The material presented covers a range of fundamental concepts necessary for solving problems in this topic. Key areas of focus include:
- Understanding numerical operations and their applications
- Mastering algebraic expressions and equations
- Breaking down word problems and translating them into mathematical forms
- Identifying and applying mathematical patterns to simplify calculations
Detailed Breakdown of Topics
The following list outlines the major areas covered, offering a deeper look into each one:
- Operations with Fractions: Techniques for adding, subtracting, multiplying, and dividing fractions
- Linear Equations: Solving for unknown variables in one-step and multi-step equations
- Graphing Points on a Coordinate Plane: Understanding coordinates and plotting points accurately
- Problem-Solving Strategies: Approaching word problems by translating them into mathematical operations
Step-by-Step Guide to Homework Solutions
In this section, we will walk you through a detailed process for solving the exercises effectively. By breaking down each problem into smaller, manageable steps, you will be able to tackle each part with precision. This approach ensures that even the most complex questions become easier to understand and solve.
Understanding the structure of each problem is key to developing a solution strategy. Start by carefully reading the question, identifying important information, and determining what is being asked. Once you’ve clarified the goal, proceed step by step, applying the appropriate methods for each part of the problem.
Breaking Down the Problem
Start by examining the problem closely and organizing the given data. This will help you identify any patterns or relationships between the numbers or variables involved. Once you’ve done that, follow these steps:
- Step 1: Identify the type of operation needed, such as addition, subtraction, multiplication, or division.
- Step 2: Apply the correct formulas or methods for that type of operation.
- Step 3: Simplify the problem by performing intermediate calculations, if necessary.
- Step 4: Double-check each step to ensure accuracy before finalizing the result.
Applying Techniques for Difficult Problems
For more complex exercises, break down the problem even further, and don’t hesitate to apply techniques such as drawing diagrams or creating tables to better visualize the relationships between elements. With consistent practice, you will become more confident in handling even the most challenging questions.
Understanding the Core Principles of Lesson 19

To successfully tackle the tasks in this section, it’s essential to grasp the fundamental principles that guide the problem-solving process. The focus is on building a strong mathematical foundation, which will help you apply your knowledge effectively across a range of questions. Mastering these concepts will also make future challenges easier to handle, as they provide the framework for more advanced topics.
Key Ideas to Focus On
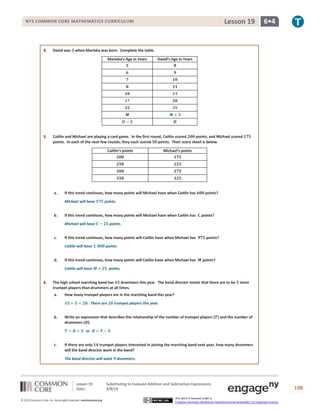
Here are the main principles you’ll need to understand in order to complete the exercises effectively:
- Basic Operations: Understanding how to manipulate numbers through addition, subtraction, multiplication, and division.
- Algebraic Thinking: Grasping the use of variables and solving equations.
- Patterns and Relationships: Identifying trends within numbers and variables that simplify problem-solving.
- Problem Translation: Converting word problems into mathematical operations.
Applying Key Concepts to Problem-Solving
Once you have a solid understanding of these core principles, you can apply them to specific problems. For instance, recognizing the need for a particular operation or identifying a pattern in a sequence will help you choose the correct method. With continued practice, these concepts will become second nature, allowing you to solve problems more quickly and accurately.
How to Tackle Complex Problems Effectively
When faced with challenging questions, breaking them down into simpler components is key to finding a solution. Complex problems often seem overwhelming at first, but with the right approach, they become manageable. The goal is to identify the best strategies and techniques that allow you to navigate through the problem step by step, ensuring accuracy and efficiency in the process.
Approach for Solving Difficult Problems

Here are several strategies that can help simplify complex problems:
- Read the Problem Thoroughly: Make sure to fully understand what is being asked before beginning the solution process.
- Break It Down: Divide the problem into smaller, more manageable parts, solving one step at a time.
- Identify Patterns: Look for common patterns or relationships between numbers or variables that may simplify the task.
- Apply Relevant Techniques: Use formulas, methods, or operations that fit the type of problem you’re dealing with.
- Check Your Work: Always verify your solution by retracing your steps to ensure accuracy.
Example of Problem Breakdown
Here’s an example of how to approach a complex question:
| Step | Action | Expected Outcome |
|---|---|---|
| 1 | Read the problem carefully | Understanding the task and key information |
| 2 | Break the problem into smaller parts | Focusing on manageable steps |
| 3 | Apply the appropriate method | Using relevant formulas or operations |
| 4 | Check and verify the results | Ensuring accuracy and correctness |
Strategies for Solving Math Questions
Solving mathematical problems requires a methodical approach that involves recognizing patterns, applying relevant formulas, and carefully working through each step. By using effective strategies, you can approach any math problem with confidence and increase your chances of finding the correct solution. This section explores a range of techniques that can simplify even the most complex questions.
Key Techniques for Success
Mastering the following strategies will help you tackle a variety of math questions:
- Understand the Problem: Read the problem thoroughly and ensure you know what is being asked before proceeding. Identify the key elements, such as numbers, variables, and operations.
- Choose the Right Method: Determine which mathematical techniques are most appropriate for the problem. Whether it’s arithmetic, algebra, or geometry, knowing which method to use is crucial for success.
- Break Down Complex Problems: For larger problems, divide them into smaller, easier-to-manage parts. Solve each part step by step, making it easier to track your progress and avoid errors.
- Use Visual Aids: For certain types of questions, drawing diagrams, charts, or tables can help visualize relationships and simplify complex calculations.
Additional Tips for Efficient Problem Solving

Along with the key techniques mentioned above, keep these additional tips in mind for improving your math problem-solving skills:
- Practice Regularly: The more you practice, the more familiar you become with different types of problems and their solutions.
- Work Backwards: In some cases, starting with the final answer and working backward can help you identify the correct process.
- Double-Check Your Work: Always verify your calculations and steps to ensure accuracy and avoid mistakes.
Common Mistakes to Avoid in Homework

When working through assignments, it’s easy to overlook small details that can lead to mistakes. Being aware of common pitfalls and developing strategies to avoid them is crucial for improving accuracy and efficiency. This section highlights the frequent errors that students make and offers practical tips to help you stay on track.
Frequent Errors in Problem-Solving
Many mistakes occur during the problem-solving process, especially when it comes to understanding the question and applying the correct method. Here are some of the most common issues:
- Misinterpreting the Problem: Often, students fail to fully understand the question, which leads to incorrect solutions. Always read the problem carefully and make sure you know what is being asked.
- Skipping Steps: Rushing through calculations or skipping intermediary steps can lead to errors. Ensure you follow the correct process and check each step before moving on.
- Overlooking Negative Signs: Forgetting to account for negative signs in equations or calculations can easily cause mistakes, especially when working with fractions or algebraic expressions.
- Incorrect Use of Formulas: Using the wrong formula or misapplying a concept can derail your entire solution. Double-check that the method you’re using is the right one for the problem at hand.
Tips for Avoiding Mistakes
In addition to being mindful of the errors listed above, consider these tips to minimize mistakes and improve the quality of your work:
- Stay Organized: Write out each step clearly and logically to avoid confusion and prevent skipping important parts of the solution.
- Double-Check Your Work: Take the time to review your solution after completing the problem. This can help you spot any mistakes you may have missed initially.
- Practice Regularly: The more you practice, the more familiar you become with the types of problems you’ll encounter. Regular practice helps reduce mistakes by reinforcing concepts.
Tips for Reviewing Lesson 19 Content
Effective review is essential to mastering the material and reinforcing the concepts you’ve learned. By taking a structured approach to reviewing, you can ensure that you fully understand the content and are prepared for any related tasks. Here are some strategies to help you review the material thoroughly and efficiently.
Review Strategies for Success
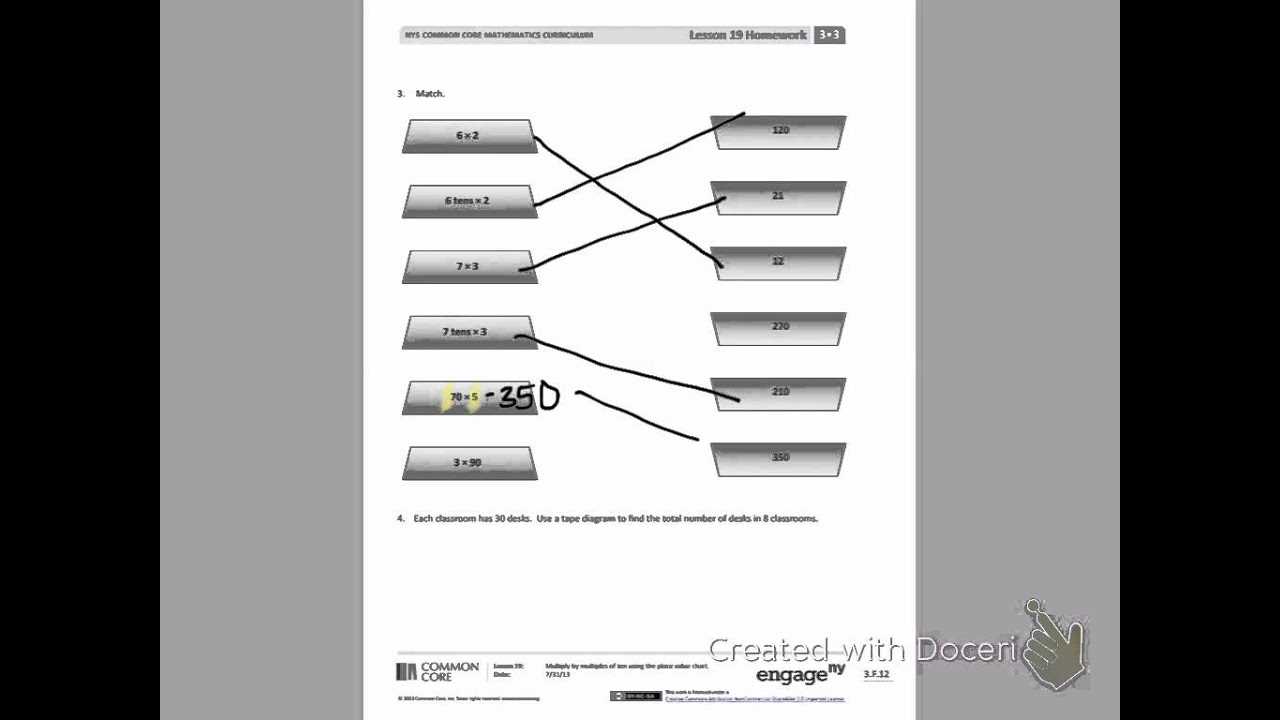
To optimize your study sessions, try these proven techniques:
- Break Down Key Concepts: Focus on one concept at a time and make sure you understand the principles before moving on to the next one.
- Create Summary Notes: Write a brief summary of the material in your own words to reinforce key points and simplify complex ideas.
- Practice Regularly: Regular practice is essential for retention. Solve a variety of problems to reinforce your understanding and identify areas that need further review.
- Use Visual Aids: Diagrams, charts, or even mind maps can help you visualize connections between concepts and clarify difficult material.
Effective Review Techniques
In addition to the general review strategies, the following techniques can help you better absorb and retain the material:
- Teach What You’ve Learned: Explaining the concepts to someone else, or even to yourself, can help solidify your understanding and highlight any gaps in your knowledge.
- Take Practice Quizzes: Testing yourself with practice quizzes or problems is a great way to assess your grasp of the material and identify areas for improvement.
- Group Study: Collaborating with others can provide new insights and different perspectives, making it easier to understand challenging concepts.
What You Need to Know About Word Problems
Word problems can often be the most challenging part of any mathematical assignment. These problems require you to translate a real-life situation into mathematical terms and solve it using appropriate methods. The key to successfully solving word problems is understanding the context, identifying the relevant information, and applying the correct approach. In this section, we’ll explore effective strategies for tackling these types of questions.
Steps for Solving Word Problems
To break down word problems efficiently, follow these key steps:
- Read the Problem Carefully: Take your time to read through the problem, ensuring you understand the context and what is being asked.
- Identify Important Information: Highlight or underline key numbers, relationships, and operations mentioned in the problem.
- Choose the Right Strategy: Decide which mathematical method to use based on the information given. This could involve addition, subtraction, multiplication, division, or other operations.
- Set Up an Equation: Translate the words into an equation that represents the relationships between the quantities. This will serve as the foundation for solving the problem.
- Solve and Check: Solve the equation, then review your work to ensure the solution makes sense in the context of the problem.
Common Challenges in Word Problems
While word problems are common in various subjects, they often present specific challenges. Here are some common difficulties students face:
- Misunderstanding the Question: Sometimes, students focus on the numbers without fully grasping what the question is asking.
- Identifying the Wrong Information: It’s easy to get distracted by unnecessary details or fail to spot the most important data in the problem.
- Difficulty in Translating Words to Math: Converting the scenario described in the problem into a mathematical equation can be tricky.
Example Word Problem
To help illustrate the process, here is an example of a word problem with its step-by-step solution:
| Problem | Jane has 5 apples. She buys 3 more apples. How many apples does Jane have now? |
|---|---|
| Step 1: Identify Information | Jane starts with 5 apples and buys 3 more. |
| Step 2: Set Up Equation | 5 + 3 = ? |
| Step 3: Solve the Equation | 5 + 3 = 8 |
| Answer | Jane now has 8 apples. |
Breaking Down Multi-Step Questions

Multi-step questions can often seem daunting due to their complexity, but with a structured approach, they become much easier to handle. These questions typically require more than one operation or method to find the correct solution. Breaking them down into smaller, manageable steps is key to solving them efficiently. In this section, we will explore how to approach these types of questions and solve them step by step.
Approach to Multi-Step Problems
To tackle multi-step questions, follow this methodical approach:
- Read the Question Thoroughly: Begin by reading the entire problem to understand all aspects of the question. Ensure you are clear on what is being asked.
- Identify the First Step: Look for the first operation or calculation you need to perform. This is often the key to starting the problem.
- Work Step by Step: Solve each step in sequence, taking care to perform the calculations correctly before moving on to the next one.
- Use Intermediate Results: Keep track of intermediate results and use them for the next step in the process. This ensures that you are building upon your progress.
- Review the Entire Problem: After completing the final step, double-check your solution by reading the question again and verifying the calculations.
Example of a Multi-Step Problem
Here’s an example to demonstrate how to break down a multi-step question:
| Problem | A bakery sells muffins at $2 each and cookies at $3 each. If a customer buys 4 muffins and 5 cookies, how much will the total cost be? |
|---|---|
| Step 1: Multiply for Muffins | 4 muffins x $2 = $8 |
| Step 2: Multiply for Cookies | 5 cookies x $3 = $15 |
| Step 3: Add the Results | $8 (muffins) + $15 (cookies) = $23 |
| Final Answer | The total cost is $23. |
By following these steps, the problem is simplified and easier to solve without missing any important details.
How to Check Your Work for Accuracy

Ensuring that your work is accurate is essential for mastering any subject. Reviewing your solutions can help you catch errors, improve your understanding, and increase your confidence. In this section, we will outline effective strategies for checking your work and ensuring that every step of the process is correct.
Steps to Verify Your Results
To check your work thoroughly, follow these important steps:
- Double-Check Calculations: Go over each calculation carefully to ensure no mistakes were made in addition, subtraction, multiplication, or division.
- Revisit Each Step: Review each step of your process. Ensure that each operation logically follows the previous one and that no important details were overlooked.
- Verify Units and Labels: Make sure you have included any necessary units or labels. These details are often overlooked but are crucial for accuracy, especially in word problems or measurement tasks.
- Reverse the Process: In some cases, reversing the steps can help verify the solution. If you used multiplication, try dividing the result to see if it checks out.
- Seek Consistency: If the problem involves multiple steps or different sections, check for consistency between your answers. A discrepancy could indicate an error.
Additional Tips for Verification

Here are some additional tips to help you catch mistakes and ensure your work is correct:
- Work Backwards: In certain problems, working backwards can help confirm your solution. This is especially useful for problems involving equations or logical steps.
- Use a Different Method: If possible, solve the problem using a different method or approach to see if you get the same result. This can serve as a quick check for accuracy.
- Take Breaks: After completing the task, take a short break before reviewing your work. This will allow you to approach it with fresh eyes and help you spot errors more easily.
By applying these techniques, you can be confident that your work is accurate and that you have mastered the material effectively.
Using Resources to Aid in Problem Solving
When facing challenging questions, it’s essential to use available resources to assist in finding the correct solution. Resources such as textbooks, online platforms, and practice materials can provide the necessary guidance to break down complex problems. In this section, we will explore how to leverage these resources effectively to improve problem-solving skills and achieve better outcomes.
Types of Resources for Effective Problem Solving
Different resources can offer varying levels of support, depending on the task at hand. Here are some types of resources that can be helpful:
- Textbooks and Class Materials: Review your class notes and textbooks for step-by-step examples. These materials often contain worked-out problems that are similar to what you’re facing, providing useful insights.
- Online Tutorials and Videos: Platforms like YouTube and educational websites offer video tutorials that explain the solution process for many types of problems. Visual aids can often make complex concepts clearer.
- Practice Worksheets: Practice sheets are an excellent way to reinforce concepts. Working through additional problems helps solidify understanding and prepares you for different types of challenges.
- Discussion Forums: Websites like Stack Exchange and other forums allow you to ask specific questions and engage with a community of experts. This is especially helpful if you’re stuck and need guidance from others.
- Instructional Apps: There are many apps designed to help with problem-solving in various subjects. These apps can provide instant feedback and often offer interactive ways to practice.
How to Use These Resources Effectively
Simply having access to these resources is not enough; using them wisely is key to successful problem-solving:
- Don’t Rely on Answers Alone: While it’s tempting to search for the solution directly, it’s important to understand the process behind the answer. Take the time to follow the solution steps to deepen your comprehension.
- Compare Multiple Sources: If one resource doesn’t make sense, consult another. Different explanations or approaches can offer a fresh perspective on the problem.
- Take Notes: As you review resources, jot down important concepts, formulas, or problem-solving strategies. These notes can serve as a reference for future tasks.
- Work in Stages: Break down problems into smaller chunks and use resources for each step. This approach ensures you understand each phase of the problem-solving process.
By effectively utilizing these resources, you can tackle difficult problems with more confidence and a clearer understanding of the material.
How Practice Makes Perfect in Education
Mastering any subject, especially complex topics, requires consistent practice and effort. This principle holds true across all fields of study, and the more time you dedicate to solving problems and reviewing material, the more confident and proficient you become. In this section, we will explore how regular practice can improve your skills, enhance understanding, and lead to better academic performance.
The Importance of Consistency
Repetition is key when it comes to learning. By repeatedly working through similar types of problems or concepts, you can strengthen your grasp of the material and improve your problem-solving strategies. Here’s how consistent practice helps:
- Reinforces Learning: Revisiting topics multiple times ensures that concepts stay fresh in your mind. It helps reinforce key ideas and formulas, making them easier to recall during assessments.
- Builds Confidence: As you become more familiar with different types of problems, you will approach new challenges with greater assurance. This confidence boosts your ability to tackle more difficult material over time.
- Identifies Weak Areas: Regular practice helps identify areas where you may need further clarification. If certain topics are challenging, you can dedicate more time to them and seek additional help if necessary.
- Develops Problem-Solving Skills: The more problems you work through, the more methods and strategies you will discover. Each problem presents an opportunity to learn a new approach, making you more adaptable in solving future questions.
Effective Ways to Practice
To get the most out of your practice sessions, it’s essential to practice strategically. Here are some methods for effective practice:
- Set Specific Goals: Focus on one concept or problem type at a time. Rather than aimlessly solving problems, target a specific skill you want to improve, such as mastering fractions or understanding algebraic equations.
- Use a Variety of Problems: Practice problems can vary in difficulty and style. By exposing yourself to a wide range of problems, you’ll be better prepared for any challenges that may arise.
- Track Your Progress: Keep a record of your practice sessions to monitor improvements. This can also help you notice patterns in the types of problems you find more difficult, so you can focus your efforts accordingly.
- Review Mistakes: Don’t just move on when you make an error. Take time to understand why you made the mistake and learn from it. This process is crucial for refining your skills.
Ultimately, practice is not just about completing tasks–it’s about making continuous progress and developing a deeper understanding of the material. The more you practice, the more proficient you’ll become, leading to greater success in academic endeavors.
Improving Speed and Efficiency in Tasks
Being able to complete tasks quickly and accurately is a valuable skill, especially when dealing with complex subjects or a large volume of work. Achieving a balance between speed and accuracy requires practice, strategy, and focus. In this section, we will explore effective methods to enhance both the speed and efficiency with which you approach assignments, ensuring you can complete them in less time while maintaining high standards.
The key to improving speed and efficiency lies in developing strong foundational skills and using proven techniques that reduce the time spent on each task. As you become more familiar with concepts and problem-solving methods, you can begin to work faster without sacrificing quality.
Here are a few strategies that can help improve your overall performance:
- Understand the Fundamentals: A solid understanding of the basic concepts and formulas allows you to solve problems more quickly. When you’re confident in the foundational knowledge, you can spend less time thinking about basic principles and focus more on applying them effectively.
- Practice Mental Math: Being able to solve simple calculations in your head rather than writing them down saves valuable time. Regular practice can help you improve your mental arithmetic and increase your overall speed.
- Use Templates or Shortcuts: Whenever possible, use templates, shortcuts, or strategies that streamline tasks. Whether it’s a formula, a pattern, or a specific method, having go-to solutions can help you complete tasks more efficiently.
- Prioritize Tasks: Not all tasks require the same amount of effort or time. Prioritize the more complex or time-consuming tasks first and tackle them when you’re most focused. This allows you to allocate time efficiently to each task.
- Avoid Multitasking: While it may seem like multitasking can increase your productivity, it often leads to mistakes and wasted time. Focusing on one task at a time helps you work more efficiently and reduces the likelihood of errors that need to be corrected later.
By incorporating these strategies into your routine, you can gradually improve the speed with which you complete tasks without compromising the quality of your work. Efficiency doesn’t mean rushing through assignments; it means becoming more proficient and strategic in your approach.
Important Formulas and Definitions for Lesson 19

In any subject, mastering key formulas and concepts is crucial for solving problems effectively. Understanding the definitions and knowing when to apply specific formulas can save time and increase accuracy. This section will cover the essential formulas and terms you need to understand in order to excel in the tasks at hand.
To ensure success, it’s important to memorize the critical principles and practice applying them to different scenarios. Below, you will find the core formulas and definitions that will help guide your approach to various types of problems.
Key Formulas

- Formula 1: The area of a rectangle: Area = Length × Width
- Formula 2: The perimeter of a square: Perimeter = 4 × Side Length
- Formula 3: The Pythagorean Theorem: a² + b² = c², used for right triangles
- Formula 4: The volume of a cylinder: Volume = π × Radius² × Height
Key Definitions
- Term 1: Area: The measure of the space inside a two-dimensional shape, typically in square units.
- Term 2: Perimeter: The total length of all sides of a polygon.
- Term 3: Radius: The distance from the center of a circle to any point on its edge.
- Term 4: Height: The perpendicular distance from the base of a figure to its topmost point.
Familiarizing yourself with these essential formulas and definitions is the first step in solving problems more efficiently. Once you are comfortable with them, you can focus on applying these principles to various scenarios, making problem-solving faster and more accurate.
How to Prepare for Future Lessons and Tests
Effective preparation is the key to mastering new material and excelling in upcoming assessments. Knowing how to organize your study time and focus on the most important topics will help you retain information and build confidence. By adopting strategic approaches to learning, you can ensure that you are well-prepared for both future lessons and exams.
In order to succeed, it’s essential to develop a study routine that works best for you. Below are some practical steps to enhance your preparation and achieve better results:
Steps to Prepare Effectively
- Create a Study Schedule: Organize your time in advance, allocating specific hours for each topic. Prioritize the most difficult material first.
- Review Previous Material: Regularly go over past lessons to reinforce your understanding and identify any areas that need improvement.
- Practice with Sample Problems: Work through example questions similar to those you might encounter on future tests. This will help you gain familiarity with the format and types of questions.
- Seek Help When Needed: Don’t hesitate to ask teachers or peers for clarification on any concepts you find challenging.
Tips for Test Preparation
- Stay Consistent: Make studying a daily habit instead of cramming the night before an exam.
- Focus on Key Concepts: Review important formulas, definitions, and concepts that are frequently tested.
- Take Breaks: Break your study sessions into manageable chunks with short breaks in between to keep your mind fresh.
- Get Plenty of Sleep: Ensure that you are well-rested before your test to help with concentration and memory retention.
By following these strategies, you can effectively prepare for upcoming lessons and tests, improving both your understanding of the material and your test performance.