
Mathematics can be challenging, especially when tackling complex problems that require deep understanding and attention to detail. This section offers valuable insights into how to approach various exercises and effectively solve them. Whether you’re struggling with particular topics or aiming to strengthen your skills, the provided guidance will help you navigate through the material step by step.
By focusing on problem-solving techniques and breaking down difficult questions into manageable parts, you can improve your ability to handle more advanced concepts. Each solution is designed to build on the knowledge gained previously, ensuring that all key principles are well understood and retained. Mastering these methods will enable you to approach similar challenges with confidence.
Learning how to correctly interpret and work through assignments can make a significant difference in your academic journey. This guide will assist you in recognizing patterns and applying logical reasoning to find solutions efficiently. Whether for practice or review, this material is a useful resource for enhancing both your problem-solving and analytical skills.
Saxon Math Course 3 Answers Overview
This section provides a comprehensive overview of solutions for the exercises in the third level of the program. The key focus is to simplify the process of tackling various problems, ensuring that learners can confidently navigate through each topic. By understanding the structure of the tasks and the approach to solving them, students can enhance their grasp of fundamental concepts and develop problem-solving strategies for more complex challenges.
Breaking Down Key Problem Areas
The material covered in this section includes a wide range of topics, from basic calculations to more intricate algebraic tasks. Each problem is accompanied by a detailed explanation, breaking down the steps involved in reaching the correct solution. By following this systematic approach, students can better understand how to apply their knowledge to different types of exercises and improve their overall performance.
Building Confidence and Mastery
Consistent practice and a clear understanding of the techniques outlined here are essential for mastering the content. This section is designed to build confidence, allowing learners to tackle increasingly difficult problems with ease. As the concepts become clearer, students will find that their ability to approach similar exercises improves, making learning both more enjoyable and effective.
Comprehensive Guide to Saxon Math Solutions

This guide offers a detailed approach to tackling problems across various levels of difficulty, focusing on clear, step-by-step explanations for each task. The primary goal is to equip students with the tools they need to navigate complex problems with confidence. By understanding the methodology behind each solution, learners can strengthen their problem-solving skills and improve their ability to handle new challenges effectively.
Each section is designed to help students break down difficult tasks into manageable steps. Solutions are presented in a logical sequence, ensuring that every concept is understood before moving on to more advanced material. This approach provides a solid foundation, making it easier for learners to retain key principles and apply them in different contexts.
| Topic | Key Concept | Solution Approach |
|---|---|---|
| Fractions | Understanding Numerators and Denominators | Breaking down fractions and finding common denominators |
| Algebra | Solving for Variables | Applying basic equations to isolate variables |
| Word Problems | Translating Text into Mathematical Operations | Identifying keywords and solving step-by-step |
By following this guide, students will gain a deeper understanding of each topic and how to approach problems in a structured way. This method not only aids in solving individual exercises but also enhances overall mathematical thinking, providing lasting benefits for future learning.
Understanding Key Concepts in Course 3

This section focuses on helping learners grasp the essential principles necessary to solve problems at the third level of the program. By understanding the core concepts, students can build a solid foundation that will enable them to tackle more complex topics in the future. The approach is designed to make difficult ideas more approachable and provide strategies for mastering each concept with ease.
Key areas of focus include:
- Understanding fractions and their applications
- Mastering algebraic expressions and solving for variables
- Learning how to work with ratios and proportions
- Developing strategies for solving word problems effectively
- Identifying patterns and applying them to different tasks
Each of these topics is broken down into smaller, manageable parts, allowing students to gain a deeper understanding. By following this structured approach, learners can ensure they fully grasp the concepts before moving on to more advanced material.
To further enhance comprehension, it is recommended to practice regularly and apply the methods learned to a variety of problems. Repetition and consistency are key to mastering these essential concepts and improving overall performance.
How to Use the Answer Key Effectively

The answer key is an essential tool for reinforcing understanding and verifying solutions to problems. By carefully referencing the provided solutions, students can ensure their approach is correct and identify any mistakes in their work. This guide will explain how to use the answer key effectively to improve problem-solving skills and achieve a better understanding of the material.
When using the answer key, it is important to:
- Attempt solving the problem independently before checking the solution.
- Review each step in the answer key to understand the reasoning behind the solution.
- Identify any differences between your solution and the provided one, then analyze where you went wrong.
- Use the explanations to clarify any concepts you may have misunderstood.
By incorporating these strategies into your study routine, the answer key will become an invaluable resource, helping you improve both your understanding and your ability to solve similar problems in the future. Always aim to learn from the process rather than simply checking answers.
Step-by-Step Solutions for Course 3 Problems

This section provides detailed, step-by-step instructions for solving problems in the third level of the program. Each solution is broken down into clear stages to help students understand how to approach various types of tasks. By following these steps, learners can better grasp the underlying principles and develop a structured method for tackling challenges.
The following table illustrates the approach used for solving typical problems in this level:
| Problem Type | Step 1 | Step 2 | Step 3 |
|---|---|---|---|
| Fractions | Identify the numerators and denominators | Find the least common denominator (LCD) | Simplify the fraction or perform the operation |
| Equations | Isolate the variable | Simplify both sides of the equation | Solve for the unknown value |
| Word Problems | Read and identify key information | Set up an equation or system of equations | Solve and interpret the result |
By following the step-by-step breakdown for each problem, students can develop a deeper understanding of the process and apply these methods to similar exercises. This structured approach helps prevent mistakes and builds confidence in solving more complex problems.
Effective Study Tips for Success

Success in solving complex problems comes from a combination of consistent practice, understanding the key principles, and developing a strong study routine. This section will highlight several tips and strategies to help students improve their performance and deepen their understanding of essential concepts. By adopting these effective techniques, learners can enhance their problem-solving abilities and achieve better results in their studies.
Here are some valuable study tips to consider:
- Review previous lessons regularly to reinforce understanding and prevent forgetting key concepts.
- Work through practice problems before checking the solutions to challenge your problem-solving skills.
- Break down complex problems into smaller, manageable parts to make them easier to solve.
- Use visual aids, such as diagrams and charts, to help understand abstract concepts.
- Take breaks between study sessions to stay focused and prevent burnout.
- Seek help from peers or tutors if a particular concept is challenging.
By incorporating these strategies into your study routine, you will not only strengthen your understanding of the material but also improve your confidence and ability to tackle new challenges effectively. Consistent practice, patience, and a structured approach are key to mastering any subject.
Common Challenges in Level 3 Problem Solving
As students progress through the third level of the program, they often encounter specific difficulties that can hinder their understanding and problem-solving abilities. Identifying and addressing these challenges early on is essential for success. This section highlights some of the most common obstacles faced by learners and offers guidance on how to overcome them effectively.
Common challenges include:
- Difficulty understanding abstract concepts such as variables and equations.
- Struggling with word problems due to difficulty translating real-world scenarios into mathematical expressions.
- Confusion around fractions, especially when performing operations like addition and subtraction.
- Failing to recognize patterns and relationships in numerical problems.
- Making errors in multi-step problems due to losing track of intermediate steps.
- Lack of confidence when faced with unfamiliar problem types or complex questions.
To address these challenges, it’s important to regularly practice problem-solving techniques, review foundational concepts, and seek additional help when needed. Breaking down complex problems into simpler components and using visual aids can also make difficult topics more manageable. With consistent effort and the right strategies, these challenges can be overcome, leading to improved skills and greater confidence in tackling new problems.
Practice Problems and Their Solutions
In order to solidify your understanding of the material, it is essential to work through practice problems that test your ability to apply the concepts you’ve learned. This section provides a series of sample problems, along with their solutions, to help you practice and evaluate your progress. By working through these problems, you can strengthen your problem-solving skills and identify areas where further review may be needed.
The following table presents practice problems, their solutions, and step-by-step approaches to solving them:
| Problem | Solution | Step-by-Step Approach |
|---|---|---|
| 5x + 3 = 18 | x = 3 | Subtract 3 from both sides: 5x = 15. Then divide by 5: x = 3 |
| 2/3 + 1/4 | 11/12 | Find the common denominator (12): 8/12 + 3/12 = 11/12 |
| What is 20% of 50? | 10 | Convert percentage to a decimal: 20% = 0.2. Multiply 0.2 × 50 = 10 |
By working through these problems and understanding the step-by-step solutions, you can gain confidence in solving similar exercises. Regular practice with problems like these is key to mastering the material and preparing for more advanced topics in the future.
Breaking Down Complex Math Questions


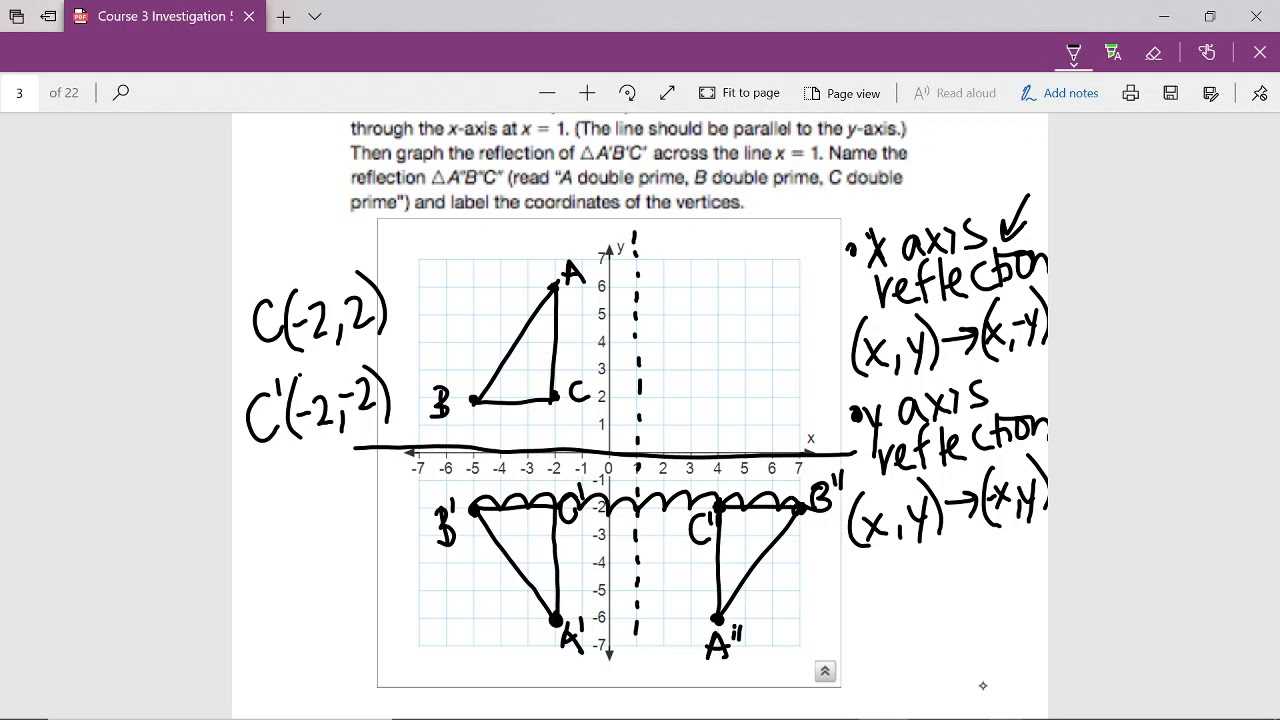
When faced with difficult problems, it’s essential to break them down into smaller, more manageable parts. This approach not only makes the problem less overwhelming but also helps identify the most efficient path to the solution. By following a structured method, you can approach complex questions with greater clarity and confidence. This section will guide you through strategies for simplifying and solving intricate problems step by step.
To tackle complex problems effectively, consider the following approach:
- Read and Understand: Carefully read the question to understand what is being asked. Identify key terms and numbers that are crucial to solving the problem.
- Break it Down: Divide the problem into smaller, more digestible parts. Work on one section at a time to avoid feeling overwhelmed.
Breaking Down Complex Math Questions
When faced with difficult problems, it’s essential to break them down into smaller, more manageable parts. This approach not only makes the problem less overwhelming but also helps identify the most efficient path to the solution. By following a structured method, you can approach complex questions with greater clarity and confidence. This section will guide you through strategies for simplifying and solving intricate problems step by step.
To tackle complex problems effectively, consider the following approach:
- Read and Understand: Carefully read the question to understand what is being asked. Identify key terms and numbers that are crucial to solving the problem.
- Break it Down: Divide the problem into smaller, more digestible parts. Work on one section at a time to avoid feeling overwhelmed.
- Apply Relevant Concepts: Think about the principles or formulas that might apply to each part of the problem. Make sure you understand how to use them before applying them.
- Work Through Step by Step: Solve each part step by step, keeping track of your work. This ensures you don’t miss any critical details.
- Review the Solution: After completing the problem, review your solution to ensure accuracy. Double-check your steps and make sure they make sense in the context of the question.
By adopting this method, even the most complex problems become more manageable. Practice with this approach will enhance your problem-solving skills, allowing you to approach difficult questions with more ease and precision.
Breaking Down Complex Math Questions
When faced with difficult problems, it’s essential to break them down into smaller, more manageable parts. This approach not only makes the problem less overwhelming but also helps identify the most efficient path to the solution. By following a structured method, you can approach complex questions with greater clarity and confidence. This section will guide you through strategies for simplifying and solving intricate problems step by step.
To tackle complex problems effectively, consider the following approach:
- Read and Understand: Carefully read the question to understand what is being asked. Identify key terms and numbers that are crucial to solving the problem.
- Break it Down: Divide the problem into smaller, more digestible parts. Work on one section at a time to avoid feeling overwhelmed.
- Apply Relevant Concepts: Think about the principles or formulas that might apply to each part of the problem. Make sure you understand how to use them before applying them.
- Work Through Step by Step: Solve each part step by step, keeping track of your work. This ensures you don’t miss any critical details.
- Review the Solution: After completing the problem, review your solution to ensure accuracy. Double-check your steps and make sure they make sense in the context of the question.
By adopting this method, even the most complex problems become more manageable. Practice with this approach will enhance your problem-solving skills, allowing you to approach difficult questions with more ease and precision.
Breaking Down Complex Math Questions
When faced with difficult problems, it’s essential to break them down into smaller, more manageable parts. This approach not only makes the problem less overwhelming but also helps identify the most efficient path to the solution. By following a structured method, you can approach complex questions with greater clarity and confidence. This section will guide you through strategies for simplifying and solving intricate problems step by step.
To tackle complex problems effectively, consider the following approach:
- Read and Understand: Carefully read the question to understand what is being asked. Identify key terms and numbers that are crucial to solving the problem.
- Break it Down: Divide the problem into smaller, more digestible parts. Work on one section at a time to avoid feeling overwhelmed.
- Apply Relevant Concepts: Think about the principles or formulas that might apply to each part of the problem. Make sure you understand how to use them before applying them.
- Work Through Step by Step: Solve each part step by step, keeping track of your work. This ensures you don’t miss any critical details.
- Review the Solution: After completing the problem, review your solution to ensure accuracy. Double-check your steps and make sure they make sense in the context of the question.
By adopting this method, even the most complex problems become more manageable. Practice with this approach will enhance your problem-solving skills, allowing you to approach difficult questions with more ease and precision.
Breaking Down Complex Math Questions
When faced with difficult problems, it’s essential to break them down into smaller, more manageable parts. This approach not only makes the problem less overwhelming but also helps identify the most efficient path to the solution. By following a structured method, you can approach complex questions with greater clarity and confidence. This section will guide you through strategies for simplifying and solving intricate problems step by step.
To tackle complex problems effectively, consider the following approach:
- Read and Understand: Carefully read the question to understand what is being asked. Identify key terms and numbers that are crucial to solving the problem.
- Break it Down: Divide the problem into smaller, more digestible parts. Work on one section at a time to avoid feeling overwhelmed.
- Apply Relevant Concepts: Think about the principles or formulas that might apply to each part of the problem. Make sure you understand how to use them before applying them.
- Work Through Step by Step: Solve each part step by step, keeping track of your work. This ensures you don’t miss any critical details.
- Review the Solution: After completing the problem, review your solution to ensure accuracy. Double-check your steps and make sure they make sense in the context of the question.
By adopting this method, even the most complex problems become more manageable. Practice with this approach will enhance your problem-solving skills, allowing you to approach difficult questions with more ease and precision.
Breaking Down Complex Math Questions
When faced with difficult problems, it’s essential to break them down into smaller, more manageable parts. This approach not only makes the problem less overwhelming but also helps identify the most efficient path to the solution. By following a structured method, you can approach complex questions with greater clarity and confidence. This section will guide you through strategies for simplifying and solving intricate problems step by step.
To tackle complex problems effectively, consider the following approach:
- Read and Understand: Carefully read the question to understand what is being asked. Identify key terms and numbers that are crucial to solving the problem.
- Break it Down: Divide the problem into smaller, more digestible parts. Work on one section at a time to avoid feeling overwhelmed.
- Apply Relevant Concepts: Think about the principles or formulas that might apply to each part of the problem. Make sure you understand how to use them before applying them.
- Work Through Step by Step: Solve each part step by step, keeping track of your work. This ensures you don’t miss any critical details.
- Review the Solution: After completing the problem, review your solution to ensure accuracy. Double-check your steps and make sure they make sense in the context of the question.
By adopting this method, even the most complex problems become more manageable. Practice with this approach will enhance your problem-solving skills, allowing you to approach difficult questions with more ease and precision.
Tips for Solving Word Problems in Level 3
Word problems can often seem intimidating because they require both reading comprehension and mathematical reasoning. However, with the right strategies, these problems become more manageable. In this section, we will cover useful tips for approaching and solving word problems effectively. By following these techniques, you can improve your ability to translate real-world scenarios into mathematical equations and solutions.
Here are some tips to help you tackle word problems:
- Read the Problem Carefully: Before attempting to solve the problem, read it several times to ensure you fully understand the scenario and what is being asked. Identify the key information and terms.
- Identify the Question: Pay close attention to what the problem is asking. Highlight the specific question so you can focus on solving for that particular unknown.
- Translate Words into Mathematical Expressions: Convert the word problem into an equation or set of operations. Look for phrases that indicate operations, such as “total” for addition or “difference” for subtraction.
- Organize the Information: Write down the known values and what you need to find. It can be helpful to draw diagrams or tables to visualize the problem.
- Work Step by Step: Solve the problem one step at a time. Don’t try to jump ahead; instead, break the problem into smaller parts and solve each one sequentially.
- Check Your Answer: Once you’ve found a solution, review your work. Make sure your answer makes sense in the context of the problem and recheck your steps for any errors.
By applying these strategies, you can improve your ability to approach and solve word problems. With consistent practice, you’ll gain confidence and develop the skills needed to tackle even more challenging problems in the future.
How Structured Learning Builds Strong Foundations

Effective learning begins with a solid foundation. In mathematics, this principle is especially important as each new concept builds upon the ones learned previously. A methodical approach to teaching ensures that students grasp fundamental concepts thoroughly before moving on to more complex ideas. This approach strengthens problem-solving skills and prepares students for higher-level challenges.
Through consistent practice and gradual progression, learners can develop a deep understanding of key principles. This ensures they are well-equipped to tackle more advanced topics in the future. The key to building a strong foundation lies in reinforcing basic skills and consistently revisiting them throughout the learning process.
Continuous Reinforcement of Core Concepts
By revisiting essential skills regularly, students strengthen their understanding and avoid gaps in knowledge. Repetition allows learners to retain information better, ensuring that foundational skills are always fresh and accessible for more complex problems.
Step-by-Step Development of Skills

Breaking down complex topics into smaller, manageable parts makes learning more accessible. Each lesson is designed to introduce new concepts at a steady pace, ensuring that students are not overwhelmed. With each new step, learners gain confidence and develop the skills necessary for success in more advanced areas.
Reviewing and Reassessing Lessons for Better Understanding

Revisiting and reflecting on previously learned material is essential for reinforcing concepts and ensuring long-term retention. This process allows learners to identify areas where they may need further clarification and helps them build a stronger foundation for more advanced topics. A thorough review not only improves understanding but also boosts confidence, enabling students to approach new challenges with a clearer perspective.
Here are some strategies to effectively review and reassess lessons:
- Revisit Key Concepts: Go back to the main points of each lesson. Make sure you understand the underlying principles before moving on to new material.
- Practice Regularly: Solve problems from earlier lessons to reinforce what you’ve learned. Consistent practice will help solidify your understanding of core topics.
- Identify Weak Areas: Focus on areas where you feel less confident. These are the sections where additional practice or clarification may be needed.
- Use Multiple Resources: If a concept is difficult to grasp, look for explanations from different sources. Sometimes a different perspective can make things clearer.
- Teach Someone Else: Explaining a concept to someone else is a powerful way to reinforce your own understanding. If you can teach it clearly, you likely understand it well.
By regularly reviewing and reassessing lessons, learners can ensure that they are building a strong and lasting understanding. This process helps to reinforce knowledge, uncover gaps, and solidify the foundation needed for tackling more challenging material in the future.