
Understanding how to represent numbers in compact ways is a crucial skill in mathematics. This approach simplifies complex calculations and makes working with large figures more manageable. Whether you’re dealing with enormous values in scientific fields or learning to solve mathematical challenges, this concept plays a key role in everyday applications.
By grasping how to work with numerical expressions efficiently, students can tackle a wide range of tasks with greater accuracy. From simplifying large figures to interpreting them in different contexts, the ability to transform numbers into a more convenient format is indispensable in many areas of study and practical scenarios.
In this guide, we will explore essential methods for converting numbers, solving problems, and avoiding common errors. With the right approach, mastering this skill will become an invaluable part of your mathematical toolkit.
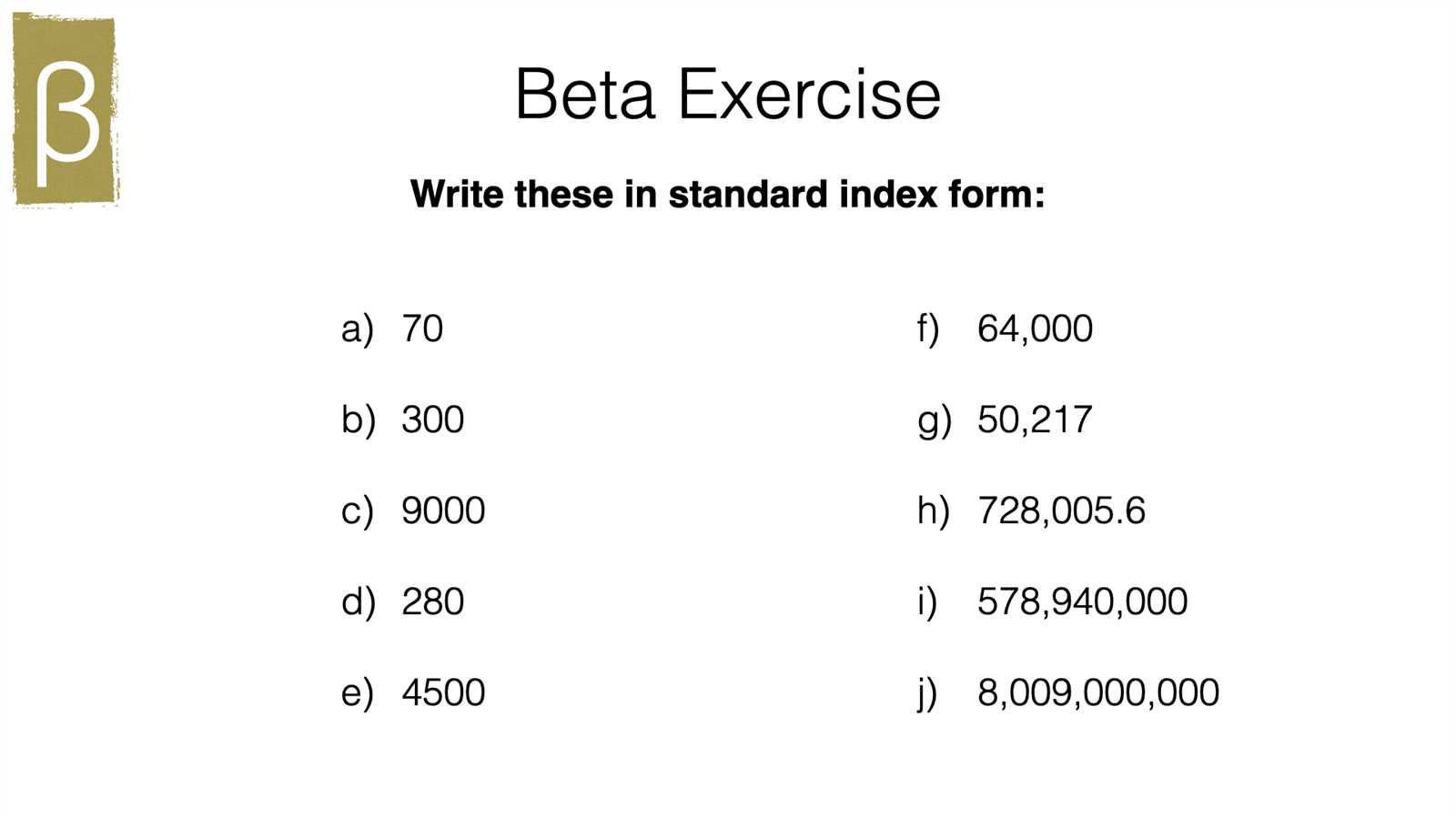
Standard Form Exam Questions and Answers
In any test or academic challenge, it is important to understand how to represent numbers in a more manageable way, especially when dealing with large or small values. Being able to express numbers succinctly not only simplifies calculations but also enhances your ability to work with data across various disciplines. This section will focus on common problem types and provide solutions that will help you approach this topic confidently.
Examples of Mathematical Problems
One of the most frequent types of problems involves converting large or small numbers into a simpler format. These tasks might require expressing values as powers of 10 or adjusting them into an easier-to-read structure. For instance, transforming a long number like 1,000,000 into a more compact representation like 1 × 10^6 can make complex calculations much simpler.
Step-by-Step Solutions to Common Problems
When tackling such problems, it’s crucial to understand the rules that govern number representation. Start by identifying the base number and the power of 10 it can be multiplied by. For example, when converting 0.00045, you can express it as 4.5 × 10^-4. Practicing these types of problems ensures that you can solve them quickly and with greater accuracy during any assessment or real-life application.
What is Standard Form in Math?
In mathematics, it’s essential to represent numbers in a way that makes them easier to work with, especially when dealing with very large or very small values. This method allows you to express such numbers more simply and compactly, making calculations faster and less prone to errors. By adopting this technique, complex equations and problems become more manageable.
When using this method, numbers are typically written as a product of a base number and a power of 10. This structure helps streamline operations and makes the values more practical for analysis and computation.
Key Characteristics of This Representation
- The number is expressed as a coefficient multiplied by 10 raised to a certain exponent.
- The coefficient is typically a number between 1 and 10.
- The exponent indicates how many places the decimal point moves to convert the number to its full form.
Examples of Practical Applications

- Large numbers in fields such as astronomy, where distances between stars and galaxies are measured in billions of light-years.
- Small numbers in scientific disciplines, such as biology, where measurements of cells or molecules are often minuscule.
Using this technique, you can work with values more efficiently in everyday problems or advanced studies.
Understanding the Basics of Standard Form

In mathematics, working with numbers that are either extremely large or small can be cumbersome. To simplify these numbers, a specific method is used that allows them to be represented in a more concise way. This approach not only helps in reducing the complexity of calculations but also makes it easier to compare and manipulate different values.
The main idea behind this technique is to express numbers as a product of a base number and a power of 10. By doing so, the values become more manageable and easier to work with in mathematical operations. The base number is usually a figure between 1 and 10, while the exponent indicates how many times the base is multiplied or divided by 10.
Mastering this method is essential for simplifying problems, especially in fields like science, engineering, and finance, where dealing with very large or very small values is common. With a solid understanding of these principles, you can quickly handle such numbers with accuracy and confidence.
Common Questions on Standard Form
When working with numbers expressed in a more compact manner, many people encounter challenges. Some of these challenges involve the process of converting numbers, understanding the rules for adjusting decimal points, or dealing with exponents. Below are some of the most frequently asked topics related to this method of representation.
Frequently Asked Topics
- How do you convert a large number into a more concise format?
- What happens when the number is smaller than 1?
- How do you determine the correct exponent when converting?
- How can negative exponents be interpreted?
- What is the correct way to handle decimal points?
Example Problems
- Convert 45,000,000 into a simpler form.
- Express 0.00032 as a more compact value.
- Write 8.9 × 10^-3 as a decimal number.
- Explain the steps to convert a number like 1,234,000 into its scientific notation.
By familiarizing yourself with these common issues, you’ll be better equipped to handle any related problems quickly and accurately. With practice, the process becomes intuitive and easy to apply in different contexts.
Key Concepts to Remember in Standard Form
To effectively work with numbers in a simplified manner, it’s essential to understand the foundational ideas behind this representation method. These core principles help ensure accuracy when converting, manipulating, or interpreting numbers expressed in this concise format. Below are some crucial concepts to keep in mind when using this approach.
The first key idea is recognizing the role of the base number and the power of 10. The base is typically a number between 1 and 10, and the exponent determines how many times the base is multiplied or divided by 10. It’s important to always adjust the decimal point correctly based on the value of the exponent.
Another vital point is understanding how positive and negative exponents affect the value. Positive exponents indicate that the decimal point moves to the right, while negative exponents shift it to the left. Mastery of these concepts will allow you to convert numbers seamlessly and solve related problems with confidence.
How to Convert Numbers to Standard Form
Converting numbers into a more manageable format is a useful skill in many mathematical applications. This method allows you to express large or small values more concisely, making calculations easier and more accurate. The process involves moving the decimal point and adjusting the exponent accordingly to fit a specific structure.
Step-by-Step Guide
To convert a number into this format, follow these simple steps:
- Identify the base number, which should be a value between 1 and 10.
- Move the decimal point in the number so that the base is in the correct range.
- Count how many places you moved the decimal point and use this count as the exponent for 10.
- If the decimal point moves to the right, the exponent will be positive. If it moves to the left, the exponent will be negative.
Examples of Converting Numbers
For example, to convert 4,500,000:
- Move the decimal point 6 places to the left, making it 4.5.
- The result is 4.5 × 10^6.
For a smaller number, like 0.00056:
- Move the decimal point 5 places to the right, making it 5.6.
- The result is 5.6 × 10^-5.
By practicing this method, you’ll gain confidence in handling numbers in this simplified format, whether working with large figures or tiny measurements.
Practice Problems for Standard Form
To master the technique of simplifying numbers, it is essential to practice solving problems that involve converting both large and small values into a more concise representation. By working through examples, you can improve your understanding of how to manipulate exponents and decimal points effectively. Below are several practice problems to help you sharpen your skills.
Conversion Challenges

Try converting the following numbers into a more compact representation:
| Original Number | Converted Form |
|---|---|
| 123,000,000 | 1.23 × 10^8 |
| 0.0000987 | 9.87 × 10^-5 |
| 450,000 | 4.5 × 10^5 |
| 0.000042 | 4.2 × 10^-5 |
Additional Problems to Solve
- Convert 8,200,000 into a more concise value.
- Express 0.0000735 as a simplified number.
- Convert 3,000,000 into a compact representation.
- Express 0.0049 as a smaller value in this format.
By practicing these problems regularly, you will become more comfortable with the process of converting numbers efficiently and accurately.
Common Mistakes in Standard Form Conversion
When converting numbers into a more manageable format, it’s easy to make certain errors that can lead to incorrect results. These mistakes often occur when dealing with decimal points, exponents, or misinterpreting the magnitude of a number. Understanding these common pitfalls can help you avoid them and improve your accuracy in solving related problems.
Common Errors in Conversion

Here are some of the most frequent mistakes people make when converting numbers:
| Mistake | Explanation |
|---|---|
| Incorrect placement of the decimal | Moving the decimal point too far left or right leads to an inaccurate base number. |
| Misunderstanding exponents | Incorrectly interpreting the exponent can cause the value to be too large or too small. |
| Forgetting to adjust the exponent | When changing the position of the decimal, failing to modify the exponent accordingly is a common mistake. |
| Confusing positive and negative exponents | Positive exponents should increase the value, while negative exponents decrease it, but they are sometimes swapped. |
How to Avoid These Mistakes
To reduce these errors, follow these simple steps:
- Always double-check the placement of the decimal point before adjusting the exponent.
- Remember that positive exponents increase the value, while negative exponents decrease it.
- Be sure to count the decimal point moves carefully and adjust the exponent accordingly.
By paying attention to these details, you can avoid common mistakes and become more proficient in converting numbers accurately.
How to Write Large Numbers in Standard Form
When dealing with extremely large numbers, it can be challenging to work with them directly. Writing these numbers in a more concise manner helps simplify calculations and makes them easier to interpret. The process involves adjusting the decimal point and using powers of 10 to express the number in a manageable form.
Steps to Convert Large Numbers
Follow these steps to convert large numbers into a simplified format:
- Identify the original number and its value.
- Move the decimal point so that the base number is between 1 and 10.
- Count how many places you moved the decimal point. This will be your exponent for 10.
- Write the number as a product of the base number and 10 raised to the power of the exponent.
Examples of Large Numbers
- Convert 15,000,000 into a compact representation:
- Move the decimal 7 places left: 1.5 × 10^7
- Convert 450,000,000 into simplified notation:
- Move the decimal 8 places left: 4.5 × 10^8
- Convert 75,000,000,000 into a more concise form:
- Move the decimal 10 places left: 7.5 × 10^10
By following these simple steps, you can easily express large numbers in a form that is easier to work with and interpret.
Using Standard Form in Real-Life Scenarios

In many practical situations, numbers can become so large or small that they are difficult to handle directly. This is especially true in fields like science, engineering, and technology, where extreme values are commonly encountered. By expressing numbers in a more compact manner, you can make calculations simpler and improve understanding of the data involved. Below are several real-life examples where this approach is essential.
Science and Astronomy

In fields like astronomy, scientists often work with extremely large numbers when measuring distances between stars, planets, and galaxies. For example, the distance from Earth to the nearest star, Proxima Centauri, is approximately 40 trillion kilometers. Writing this as a simplified value helps astronomers express such distances more easily and make comparisons across vast scales.
Technology and Computing

In computing, data storage capacities and processing speeds are often expressed using very large or small numbers. For instance, the storage capacity of modern hard drives might be measured in gigabytes (GB) or terabytes (TB), which are represented by large values like 1,000,000,000,000 bytes. Representing these numbers in a more manageable form ensures efficient communication of data storage capabilities and speeds.
Environmental Studies
Environmental scientists use compact number representations when dealing with measurements like the population of bacteria in a sample or the concentration of pollutants in the air. These values often require a large degree of precision and are more easily managed when written in a concise format.
In these various contexts, simplifying numbers not only makes them more readable but also allows for easier comparison and calculation, which is crucial for making informed decisions in fields ranging from healthcare to space exploration.
Steps to Solve Standard Form Equations
Solving equations expressed in a compact number format involves following a clear set of steps to simplify and manipulate the expression correctly. These steps can help ensure that even complex equations are manageable and solvable. Whether you are dealing with polynomial equations or scientific measurements, the process remains the same. Below are the key steps to follow when solving these types of equations.
Step 1: Identify the Base Number and Exponent
The first step is to recognize the base number and the exponent used in the equation. For example, in an equation like 3 × 10^4, the base number is 3, and the exponent is 4. Identifying these components is essential to understanding how the equation will behave as you solve it.
Step 2: Simplify the Base Number

If the base number is already between 1 and 10, no changes are needed. However, if the base number is greater than or less than this range, you must adjust the decimal place accordingly, and adjust the exponent to maintain the correct value.
Step 3: Perform the Required Mathematical Operations
Once the base number is simplified, proceed with the necessary mathematical operations. This may include addition, subtraction, multiplication, or division, depending on the equation’s structure. Be sure to apply the operations to both the base number and the exponent as required.
Step 4: Adjust the Exponent When Necessary
During the process of simplification, you may need to adjust the exponent. This is done to ensure that the equation remains in a correct and consistent form. Pay attention to the movement of the decimal point, as this directly impacts the exponent’s value.
Step 5: Check the Final Result
After performing the calculations, verify the final result. Ensure that the base number is within the correct range (between 1 and 10) and that the exponent is accurate. Double-check for any calculation errors or misinterpretations of the values to ensure your solution is correct.
By following these steps, you can effectively solve equations expressed in compact notation and ensure the accuracy of your results, no matter how complex the equation may be.
Benefits of Learning Standard Form
Mastering the technique of expressing numbers in a compact way offers numerous advantages in various fields of study and everyday life. Understanding how to simplify large or small numbers not only aids in making calculations more efficient but also enhances one’s ability to solve problems across different subjects. Below are some key benefits of learning how to represent numbers in this simplified manner.
- Improved Efficiency: Converting numbers into a concise format reduces the need to handle large digits, making mathematical operations faster and more manageable.
- Enhanced Understanding of Complex Data: By simplifying large or small figures, it becomes easier to analyze and compare data, especially in subjects like science, economics, and engineering.
- Better Accuracy in Calculations: Working with smaller, more manageable values can help reduce the likelihood of errors, especially in complex mathematical operations.
- Practical for Real-Life Applications: Whether dealing with financial data, scientific measurements, or technological statistics, compact number representation helps communicate values more clearly and effectively.
- Stronger Analytical Skills: Learning this concept strengthens problem-solving abilities and promotes logical thinking by requiring individuals to break down complex numbers into simpler, more accessible forms.
Whether you’re a student, a professional, or someone working with data regularly, mastering this technique offers a range of practical advantages. The ability to express numbers in a more understandable format plays a significant role in improving overall efficiency and precision in various fields.
How Standard Form is Used in Science
The use of compact number representation is essential in science, particularly when dealing with extremely large or small values. In fields like physics, chemistry, and astronomy, numbers can span several orders of magnitude, making traditional notation cumbersome. By converting these values into a simpler format, scientists can work more efficiently and communicate results more clearly.
- Astronomy: Distances between celestial bodies, such as stars and galaxies, are often expressed using this method. For instance, the distance from Earth to a star can be written as a number in the billions or even trillions of kilometers, which is far more manageable in compact notation.
- Physics: In particle physics, scientists often deal with incredibly tiny measurements, such as the mass of subatomic particles, which are expressed using a simplified format to avoid writing long decimal numbers.
- Chemistry: Concentrations of solutions and quantities in chemical reactions are often represented using this technique, especially when dealing with extremely low concentrations or reaction rates.
- Engineering: Engineers use compact notation to represent physical constants, such as the speed of light or gravitational constants, which are fundamental to calculations in various fields of science and technology.
Overall, this method of representation makes complex scientific data easier to handle, analyze, and share, allowing for greater precision and clarity in scientific research and communication.
Applying Standard Form in Physics
In the realm of physics, dealing with both extremely large and small numbers is a common challenge. From the vast distances between celestial bodies to the minuscule sizes of subatomic particles, representing these values in traditional notation would be unwieldy. This is where simplified numerical expressions come into play, allowing physicists to handle complex data more efficiently.
- Astronomical Distances: When measuring vast distances in space, such as the distance from Earth to distant stars, the numbers involved can be astronomical. Expressing these values using a compact notation makes them easier to understand and work with, reducing errors in calculations.
- Subatomic Particles: In particle physics, scientists work with minuscule measurements, like the mass or size of particles, which are often expressed in simplified notation for better clarity. These tiny values would otherwise require an impractically long series of zeros in decimal notation.
- Scientific Constants: Fundamental constants like the speed of light or Planck’s constant are represented in a compact format, making it easier for physicists to incorporate them into complex equations and calculations without losing precision.
- Energy Levels: In quantum mechanics, energy levels of particles such as electrons in atoms are often expressed using this technique. This allows for clearer, more concise communication of results in theoretical physics and experimental data.
Using this method in physics ensures that calculations are not only easier to perform but also more accurate, reducing the chance of errors in theoretical and experimental work. It also aids in the clear communication of complex concepts across the scientific community.
Tips for Standard Form Exam Success
Mastering the use of simplified numerical expressions is essential for tackling various types of problems. Understanding how to convert large or small numbers into a more manageable format can make a significant difference in your ability to solve problems accurately and efficiently. With the right approach and practice, achieving success in this area becomes much more attainable.
Key Strategies for Success

By following these practical tips, you can improve your ability to solve problems involving large and small numbers quickly and correctly:
- Practice Regularly: Regular practice with different types of problems will help solidify your understanding of numerical representations. The more you practice, the more confident you’ll feel when faced with complex problems during assessments.
- Understand the Basics: Ensure that you fully grasp how to convert numbers, perform calculations, and interpret results. A solid foundation will help you tackle more challenging problems with ease.
- Learn to Identify Patterns: Recognizing patterns in the way numbers are represented or manipulated can save valuable time during tests. By learning these patterns, you’ll be able to apply solutions faster and more efficiently.
- Use a Calculator Wisely: Some exams may allow you to use a calculator. Get familiar with the functionality of your calculator to perform conversions and calculations accurately without wasting time on manual steps.
Important Dos and Don’ts
To further improve your performance, make sure to follow these dos and don’ts:
| Do | Don’t |
|---|---|
| Check your work for accuracy after performing conversions. | Skip steps or rush through calculations. |
| Break down complex problems into smaller, manageable steps. | Overcomplicate simple problems. |
| Review key concepts before the assessment. | Ignore reviewing the foundational principles. |
| Stay calm and focused under pressure. | Let stress affect your performance. |
By applying these strategies, you can greatly increase your chances of success in any problem-solving situation involving these types of numerical representations. With practice and preparation, you’ll feel more confident and capable of handling any challenges that come your way.
Mastering Exponents in Standard Form
Exponents play a critical role in simplifying large and small numerical values, making them more manageable. Understanding how to use exponents effectively in various mathematical contexts can help streamline calculations and improve accuracy. When dealing with powers of ten, mastering the manipulation of exponents is essential for success, especially in scientific, engineering, and technical fields.
Exponents are typically used to express numbers that are either very large or very small in a compact and efficient manner. By adjusting the exponent, one can represent a wide range of values, making complex calculations more accessible and easier to handle.
Understanding the Basics of Exponents
Before diving into complex problems, it is important to have a strong grasp of the fundamental rules of exponents. Here are some key concepts to keep in mind:
| Rule | Description |
|---|---|
| Product Rule | When multiplying powers with the same base, add the exponents. Example: a^m × a^n = a^(m+n). |
| Quotient Rule | When dividing powers with the same base, subtract the exponents. Example: a^m ÷ a^n = a^(m-n). |
| Power Rule | When raising a power to another power, multiply the exponents. Example: (a^m)^n = a^(m×n). |
| Negative Exponent Rule | A negative exponent indicates the reciprocal of the base raised to the positive exponent. Example: a^(-n) = 1/a^n. |
Applying Exponents in Calculations

Once you are familiar with the basic exponent rules, you can apply them to solve problems involving numbers expressed as powers of 10. This is particularly useful in scientific notation, where exponents help simplify the process of dealing with extremely large or small quantities.
- Multiplying numbers with exponents: When multiplying numbers in exponential form, you simply add the exponents of the powers of 10. For example, 10^3 × 10^4 = 10^7.
- Dividing numbers with exponents: When dividing, subtract the exponents of the powers of 10. For example, 10^5 ÷ 10^2 = 10^3.
- Converting large numbers: To convert a large number into a more manageable expression, use a power of 10. For instance, 6,000 = 6 × 10^3.
By applying these rules and practicing regularly, you can become proficient in handling exponents, making it easier to manipulate complex values, simplify problems, and solve them with greater speed and precision.
Visualizing Standard Form with Graphs
Representing numbers visually can significantly improve understanding, especially when dealing with large or small values. Graphs offer a clear way to illustrate how certain numbers behave and can highlight patterns that are not immediately obvious from raw data. When using powers of ten, graphs can help provide a better grasp of the scale of values and their relationships.
In mathematical contexts, numbers expressed in exponential notation are often plotted on graphs to show trends, distributions, or changes over time. Understanding how to translate these numbers into visual form allows for easier interpretation and comparison, particularly when working with very large or small data sets.
Understanding Graphical Representation of Powers of Ten

When working with values that are expressed as powers of ten, you can visualize them on a logarithmic scale or a linear scale. Each type of graph offers unique advantages depending on the range and type of data you’re working with.
- Logarithmic scale: A logarithmic scale is particularly useful for plotting large data sets where values span multiple orders of magnitude. In this type of graph, each unit increase on the scale represents a tenfold increase in the value, which makes it easier to compare values that differ greatly in size. For example, 10^2 and 10^5 would appear closer together on a logarithmic scale than they would on a linear scale.
- Linear scale: In contrast, a linear scale is used when differences between numbers are more consistent. This scale is useful for visualizing smaller ranges of values, where the magnitude of numbers doesn’t change dramatically.
Graphing Exponential Values
To plot numbers that are expressed as powers of ten, follow these steps:
- Identify the base value (the number being multiplied by a power of ten).
- Determine the exponent and calculate the value of the number. For example, 10^3 = 1000 or 10^-2 = 0.01.
- Plot the calculated value on the appropriate graph, ensuring that the correct scale is used (logarithmic or linear).
By using graphs, you can easily compare exponential values and observe their relationships. This method is often employed in fields such as science, economics, and engineering, where data can span a wide range of magnitudes.
How to Avoid Errors in Standard Form Exams
When working with numbers expressed in exponential notation, it’s easy to make mistakes that can lead to incorrect answers. These errors can range from simple miscalculations to misunderstandings of the underlying concepts. To minimize the risk of mistakes, it is important to follow a set of strategies that help ensure accuracy and confidence during assessments.
First, focus on understanding the basic principles behind exponential notation. Knowing how to manipulate powers of ten and recognizing when to adjust the decimal point will provide a strong foundation. Secondly, practice solving problems regularly to reinforce these concepts and familiarize yourself with common pitfalls.
Additionally, it’s important to carefully read each problem and pay attention to any given instructions. Misinterpreting the problem can lead to unnecessary mistakes. Double-check your calculations and the placement of decimal points, especially when converting or simplifying numbers.
Common Mistakes to Avoid
- Incorrect decimal placement: One of the most common errors is misplacing the decimal point when converting or simplifying numbers. Always ensure that you adjust the decimal point correctly according to the exponent’s value.
- Forgetting to adjust the power: When moving the decimal point, remember to also adjust the exponent. If the decimal point moves to the left, the exponent increases, and if it moves to the right, the exponent decreases.
- Misinterpreting the problem: Be cautious when reading the problem. Sometimes, the numbers may require you to perform multiple steps, like converting from one notation to another, and missing this step can lead to errors.
Tips for Accuracy
- Practice regularly with a variety of problems to build familiarity with the process.
- Write down each step of your solution to help catch any errors as you work.
- Double-check your work before submitting to ensure all values are accurate and all steps have been followed correctly.
By staying focused, practicing diligently, and being mindful of common mistakes, you can approach problems involving powers of ten with confidence and avoid errors during assessments.