
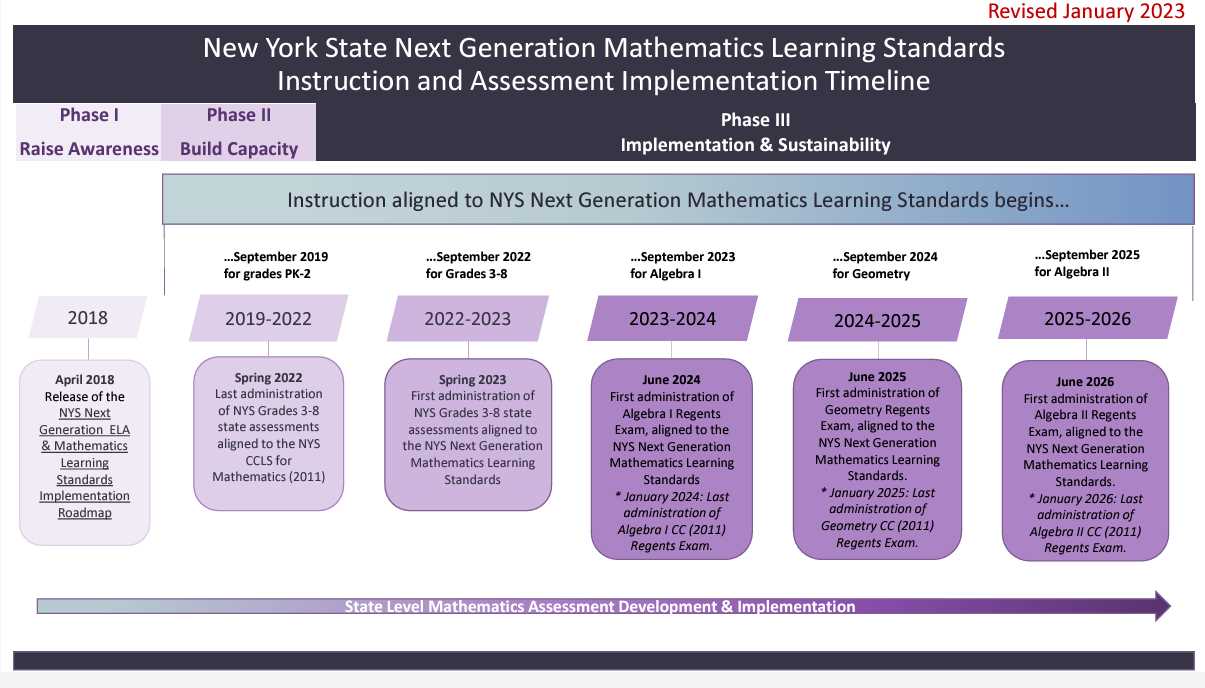
Preparing for a major math assessment can be a daunting task, but with the right approach, it becomes an opportunity to showcase your knowledge and skills. This guide will help you navigate the critical aspects of your upcoming evaluation, providing you with the tools to tackle each problem confidently and efficiently. Whether you’re focusing on complex equations, problem-solving strategies, or test-taking techniques, you’ll find the resources you need to succeed.
Understanding the structure of the exam and knowing what to expect is crucial for effective preparation. In this article, we break down the most important concepts, suggest helpful study practices, and walk you through practical examples to ensure you are fully equipped when the day arrives. By honing your abilities in these key areas, you’ll improve both your performance and your overall confidence.
From step-by-step solutions to common challenges, this resource aims to guide you through every stage of your preparation, ensuring you are ready to face the test head-on. With a strategic approach, dedication, and the right mindset, you can turn your studying into success.
Mathematics Assessment Solutions
When preparing for a key mathematics exam, understanding the types of questions and the best strategies for solving them is essential. This section provides a detailed look at the expected problems, offering step-by-step guidance on how to approach each one effectively. By familiarizing yourself with the common question formats and methodologies used, you can enhance your ability to work through complex problems with ease.
In addition to the key problem-solving techniques, this section presents detailed explanations and solutions for a range of typical exam questions. These will serve as a useful reference, helping you identify patterns in problem types and understand how to apply your knowledge accurately under exam conditions. The goal is to provide clarity and insight into the process, ensuring you feel well-prepared and confident as you approach the test.
With a focus on practical applications, this resource equips you with the tools to tackle the most challenging sections of the test. Whether you’re revisiting foundational concepts or fine-tuning advanced strategies, you’ll find the answers and methods needed to excel.
Overview of Mathematics Exam Structure
The assessment is designed to evaluate your understanding and proficiency in various mathematical concepts, focusing on problem-solving, critical thinking, and application skills. It covers a broad range of topics that are fundamental to higher-level mathematics, requiring you to demonstrate both your theoretical knowledge and practical abilities. This exam tests not only your ability to solve individual problems but also your capacity to apply mathematical reasoning in different contexts.
The exam is divided into multiple sections, each targeting different mathematical areas. These sections are structured to test your knowledge through a combination of multiple-choice questions, short answer problems, and extended response tasks. By understanding the structure of the test, you can better prepare for the types of questions you will encounter and develop the skills needed to address each one effectively.
In preparation, it’s important to familiarize yourself with the key themes and topics that will be assessed. A strategic approach to reviewing these areas will help you identify any gaps in your knowledge and focus your efforts on the most critical aspects of the material. Practicing past questions and understanding their solutions can significantly improve your performance and boost your confidence on the day of the test.
Key Topics Covered in Mathematics Curriculum
The exam assesses a wide array of mathematical concepts that are crucial for higher education and real-world applications. Understanding these core topics will ensure you’re well-prepared for the challenges the test presents. The following areas are essential for success and are frequently tested:
- Linear Equations and Inequalities
- Quadratic Functions and Their Graphs
- Systems of Equations and Inequalities
- Exponential and Logarithmic Functions
- Polynomials and Rational Expressions
- Sequences and Series
- Complex Numbers and Their Operations
- Probability and Statistics
- Mathematical Modeling and Applications
Each of these topics requires a solid understanding of both theoretical principles and practical problem-solving techniques. You will need to be comfortable manipulating equations, solving for unknowns, and applying mathematical reasoning to a variety of contexts. Mastering these key areas will help you navigate the test with confidence and accuracy.
Additionally, it’s important to understand how these topics interrelate. For example, systems of equations may be used in conjunction with quadratic functions, and the principles of probability may apply to statistics-related questions. A well-rounded understanding of these concepts will be essential for tackling more complex problems that integrate multiple areas of mathematics.
Understanding the Exam Format
To succeed in any standardized assessment, it’s essential to familiarize yourself with its structure. The test consists of multiple sections designed to assess your knowledge and problem-solving abilities across various mathematical domains. Each section includes a blend of question types, ranging from multiple-choice to open-ended tasks, aimed at evaluating both your conceptual understanding and practical application skills.
Exam Structure Overview
The format is divided into different sections, each targeting specific mathematical concepts. Below is an overview of how the exam is generally structured:
| Section | Question Type | Weight |
|---|---|---|
| Multiple-Choice Questions | Choose the correct answer from a list of options | 40% |
| Short-Answer Problems | Provide a direct answer, often with a brief explanation | 30% |
| Extended Response | Longer problems requiring detailed steps and explanations | 30% |
Time Management and Strategies
Each section is timed to ensure you can demonstrate both speed and accuracy. Proper time management is key to making sure you don’t spend too much time on any one question. The multiple-choice section is typically faster to complete, while the extended response section may require more time and attention to detail. Practicing past papers will give you a good sense of how to pace yourself throughout the exam.
How to Approach Mathematics Questions
Successfully tackling mathematical questions requires a strategic approach that involves understanding the problem, applying relevant concepts, and executing clear steps to reach the solution. By breaking down each question into manageable parts, you can avoid feeling overwhelmed and systematically solve each problem. The following guidelines will help you build a structured plan to address different types of questions efficiently.
Step-by-Step Strategy
Before jumping into solving any problem, it’s essential to follow a structured approach that will guide you through each task:
- Read the question carefully: Make sure you understand exactly what the problem is asking. Highlight key information and identify the variables involved.
- Identify the relevant concepts: Determine which mathematical principles or formulas apply to the question. This might involve recognizing patterns or recalling methods you’ve learned.
- Break it into smaller parts: If the problem seems complicated, break it down into smaller steps. Solve each step systematically before combining your results.
- Check your work: After solving, review each step and ensure there are no calculation errors or missed details in your solution.
Tips for Different Question Types
Each question type on the test requires a different approach. Here’s how to handle them effectively:
- Multiple-Choice Questions: Eliminate obviously incorrect choices first, then review the remaining options. If you’re unsure, try plugging the choices back into the problem.
- Short-Answer Questions: Provide direct answers, but always show your work. Even if the answer is correct, showing the steps can earn you partial credit.
- Extended Response Questions: Take extra time to explain each step in detail. Write clear, logical explanations of your thought process and justify each calculation.
With these strategies, you’ll be well-equipped to approach each question confidently and methodically, improving your chances of performing well on the exam.
Top Strategies for Exam Success
Achieving success in a challenging mathematics assessment requires more than just understanding the material–it involves developing effective strategies for both preparation and test-taking. By applying the right techniques, you can maximize your potential, reduce stress, and perform at your best. Here are some key strategies that will help you succeed in the exam.
Effective Preparation Methods
Preparation is the cornerstone of exam success. The more thoroughly you prepare, the more confident you’ll feel when you take the test. Consider the following tips to optimize your study time:
- Create a Study Plan: Set a clear schedule and break your study sessions into manageable chunks. Focus on one topic at a time and allocate more time to areas where you need improvement.
- Use Past Exams: Practice with previous tests to familiarize yourself with the question formats and types of problems you may encounter. This will help you identify common patterns and question styles.
- Review Key Concepts: Ensure you understand the foundational principles of the subject. A strong grasp of the basics will make more complex problems easier to solve.
- Focus on Weak Areas: Spend extra time on topics that you find challenging. Revisit concepts that you struggle with and practice related problems until you feel more comfortable.
Test-Day Tips for Success
On the day of the exam, it’s important to stay calm and manage your time effectively. Follow these strategies to ensure you’re fully prepared for test day:
- Get Enough Rest: A good night’s sleep before the exam is essential. Being well-rested will help you stay focused and think clearly during the test.
- Time Management: Allocate time for each section based on its weight and difficulty. Don’t spend too long on any single problem, and keep track of your progress.
- Read Questions Carefully: Take your time to understand what each question is asking before you begin. Misinterpreting a question can lead to mistakes.
- Stay Calm and Focused: If you encounter a difficult problem, don’t panic. Skip it and return later if necessary. Keeping a level head will help you think more clearly and solve problems more effectively.
By following these strategies, you’ll improve both your preparation and performance, setting yourself up for success on exam day.
Common Mistakes to Avoid in Mathematics
When preparing for a complex math exam, even small errors can have a significant impact on your overall score. Many students fall into common traps that can easily be avoided with proper preparation and attention to detail. Recognizing these mistakes and understanding how to avoid them will help you perform at your best and increase your chances of success.
Calculation Errors
One of the most frequent mistakes made during exams is simple calculation errors. These can occur when you rush through a problem or misread numbers. To prevent these errors, always double-check your calculations, especially when dealing with fractions, exponents, or negative numbers.
- Misplacing decimal points–This can drastically change the result of your answer. Take extra care when dealing with decimals.
- Incorrectly applying operations–For example, confusing the order of operations or adding instead of subtracting.
- Omitting steps–Skipping intermediary steps may lead to incorrect results or missed details.
Misunderstanding the Problem
Another common mistake is not fully understanding the problem before attempting to solve it. This can result in applying the wrong method or formula. Always read the question carefully and identify what is being asked before proceeding with your solution.
- Overlooking key information–Sometimes, important details are hidden within the question. Take time to identify all relevant information.
- Ignoring units or variables–Make sure you pay attention to all variables or units mentioned in the problem. These details often change the approach needed.
- Rushing through word problems–In word problems, misinterpreting the situation or the question can lead to errors in your solution strategy.
By being mindful of these common mistakes and practicing your skills, you can approach the exam with greater accuracy and confidence.
How to Practice for the Mathematics Test

Effective preparation is essential for doing well on any challenging exam, and practicing regularly is one of the best ways to improve both your skills and confidence. By working through a variety of problems, you can solidify your understanding of key concepts and become familiar with the types of questions you’ll encounter. This section outlines proven methods to help you practice efficiently and maximize your study time.
Build a Solid Study Plan
A well-structured study plan is crucial for focused and productive practice. Here are some strategies to help you create a plan that works for you:
- Identify your weak areas: Start by reviewing past materials and pinpoint the topics that challenge you the most. Focus your efforts on these areas to improve your overall performance.
- Set realistic goals: Break your study sessions into manageable time blocks and set specific goals for each one, such as completing a certain number of problems or mastering a specific topic.
- Review consistently: Rather than cramming all at once, incorporate daily or weekly reviews to reinforce what you’ve learned and ensure long-term retention.
Practice with Past Papers
One of the best ways to prepare for the test is by working through past exam papers. These will give you a sense of the question format, the level of difficulty, and the common themes tested. Here’s how to approach past papers:
- Time yourself: Simulate real exam conditions by timing yourself when working through practice tests. This will help you manage your time effectively on test day.
- Analyze your mistakes: After completing a practice exam, go over your mistakes carefully. Understand why you made each error and how you can avoid it in the future.
- Focus on problem areas: If you struggle with certain types of questions, make sure to do additional practice focused on those problem types until you feel more confident.
Use Online Resources and Tools
In addition to textbooks and past papers, online resources offer interactive ways to practice and test your skills. Consider using:
- Interactive quizzes: Many educational websites provide quizzes that give immediate feedback on your answers, allowing you to quickly identify and correct errors.
- Video tutorials: Sometimes, visual explanations can make difficult concepts clearer. Watching instructional videos can help reinforce topics that you may find challenging.
- Math apps: There are various apps available that provide practice problems, step-by-step solutions, and tips on improving your skills.
With focused practice and the right resources, you can build the skills necessary to perform confidently on your mathematics test.
Mathematics Test Solution Guide for June 2025

Having access to a detailed solution guide is an invaluable resource when preparing for an important mathematics assessment. It not only helps you check your work but also provides insights into the step-by-step methods used to solve problems correctly. This section will provide key solutions to common question types encountered in the test, allowing you to better understand how to approach and solve them.
Understanding the Solution Process

While knowing the correct answer is important, understanding the reasoning behind each solution is even more valuable. Here, we’ll break down some of the key steps involved in solving typical problems. By reviewing the solution processes, you’ll be able to apply similar strategies to new problems with confidence.
- Step 1: Carefully read the problem to identify what is being asked. Pay attention to key numbers, variables, and operations that will guide you through the solution.
- Step 2: Apply the appropriate mathematical principles, whether it’s solving an equation, simplifying an expression, or interpreting data. Follow the correct order of operations to avoid mistakes.
- Step 3: Solve the problem step by step. Ensure that each calculation is accurate before moving on to the next step.
- Step 4: Double-check your final answer, ensuring it makes sense within the context of the problem.
Example Problems and Solutions
Below are a few example problems along with their detailed solutions to give you an idea of how to approach similar questions in the actual exam:
- Problem 1: Solve the equation 2x + 5 = 13.
Solution: First, subtract 5 from both sides: 2x = 8. Then, divide both sides by 2 to get x = 4.
- Problem 2: Simplify the expression (3x + 2) – (4x – 5).
Solution: Distribute the negative sign and combine like terms: 3x + 2 – 4x + 5 = -x + 7.
By reviewing the solutions to these sample problems, you can begin to recognize patterns and apply similar strategies to the questions you will face. The key to success is not just finding the right answer, but understanding the reasoning behind it, so that you can approach any problem with a clear strategy.
Detailed Solutions to Exam Questions
Understanding how to approach and solve problems correctly is crucial for success in any exam. This section provides step-by-step solutions to some common types of problems typically seen in assessments. By breaking down each question into manageable parts, you can better understand the problem-solving process and improve your ability to handle similar questions on test day.
Step-by-Step Problem Solving
When solving problems, it’s important to follow a logical sequence to ensure accuracy. Below is a detailed solution to a common problem type, demonstrating the necessary steps to reach the correct answer. Review each step carefully to understand how to apply these methods to other problems.
| Step | Action | Result |
|---|---|---|
| 1 | Identify the problem and variables involved. | Recognize the equation or expression that needs to be solved or simplified. |
| 2 | Apply the appropriate operation or formula. | Use algebraic or arithmetic rules to simplify or solve the expression. |
| 3 | Perform the calculations step by step. | Ensure each operation is done correctly to avoid errors. |
| 4 | Review the solution for correctness. | Double-check your work to ensure the final answer is accurate. |
Example Problem and Solution
Here’s an example problem with its detailed solution:
Problem: Solve the equation: 4x – 7 = 9
Solution:
- Step 1: Add 7 to both sides of the equation:
4x – 7 + 7 = 9 + 7
Result: 4x = 16
- Step 2: Divide both sides by 4 to solve for x:
4x / 4 = 16 / 4
Result: x = 4
By following these steps, we find that the solution to the equation is x = 4.
Practicing with similar problems and reviewing detailed solutions will help you become more proficient in solving a wide range of problems efficiently and accurately.
Tips for Solving Complex Mathematics Problems
Tackling complex problems requires a combination of strong foundational knowledge, problem-solving strategies, and careful attention to detail. While difficult questions may initially seem overwhelming, breaking them down into smaller, manageable parts can make them more approachable. This section provides helpful tips for approaching and solving intricate problems effectively.
Approach Problems with a Structured Method
When faced with challenging problems, having a structured approach can make all the difference. Follow these steps to ensure you address every aspect of the question methodically:
- Understand the Problem: Carefully read the question and identify what is being asked. Look for key terms and variables that will guide your solution process.
- Organize Your Information: Write down all the given values and make a note of any formulas or rules that may apply. This helps to clarify what is needed and how to proceed.
- Choose the Right Strategy: Determine the best approach for solving the problem. Whether it’s applying an equation, simplifying an expression, or working with a graph, select the most effective method for the task at hand.
Use These Helpful Techniques
For more complex problems, it’s crucial to use specific strategies to break them down. The following techniques can help streamline your work:
- Work Backwards: Sometimes, working backwards from the solution can provide valuable insight. This can be especially helpful in problems where you are asked to verify or check the result.
- Substitute Known Values: When possible, substitute numbers or known values into the equation to reduce complexity. This makes it easier to identify patterns or simplify calculations.
- Use Estimation: For problems that seem too complex to solve exactly, estimate the answer first. This gives you a rough idea of what to expect and can guide your more detailed calculations.
Practice and Refine Your Skills

Complex problems often involve multiple steps and concepts. The more you practice, the better you’ll become at recognizing patterns and applying the right techniques quickly and accurately. Regular practice with a variety of problem types will help build your confidence and ability to tackle any question that comes your way.
By implementing these strategies, you’ll be well-equipped to handle even the most challenging problems, improving both your problem-solving efficiency and your overall performance on the test.
Using Past Exams for Preparation
One of the most effective ways to prepare for any exam is by practicing with past test papers. These materials offer valuable insight into the structure of the questions, the types of topics covered, and the level of difficulty you can expect. By reviewing previous exams, you can familiarize yourself with the test format and identify common patterns, helping you feel more confident and prepared on exam day.
Working through past papers also allows you to refine your time-management skills, as you learn how to allocate the right amount of time for each question. Moreover, practicing under timed conditions can simulate the pressure of the actual exam, improving your focus and performance.
How to Effectively Use Past Exams
Simply reviewing past exams isn’t enough–it’s important to use them strategically to maximize your preparation. Here are some steps to ensure you’re making the most out of these resources:
- Start with Recent Papers: Begin by practicing with exams from the last few years. These are more likely to reflect the current format and trends in the test.
- Review the Solutions: After completing a past exam, thoroughly review the solutions, especially for questions you got wrong. This will help you understand where you went wrong and what steps you can take to improve.
- Time Yourself: To simulate the exam environment, time yourself while working through past papers. This helps you gauge how long you should spend on each section and keeps you from running out of time during the real exam.
- Track Your Progress: Keep track of how well you perform on each practice test. Over time, you’ll see improvements in both accuracy and speed, which will boost your confidence.
Benefits of Practicing with Past Exams
There are numerous advantages to incorporating past exams into your study routine:
- Familiarity with Question Types: You’ll become comfortable with the kinds of questions typically asked, which reduces anxiety on test day.
- Identifying Common Mistakes: Reviewing past exams helps pinpoint recurring mistakes and weak areas, so you can focus your revision on those topics.
- Improved Time Management: Practicing under exam conditions helps you develop a strategy for answering questions efficiently, ensuring that you can complete the exam on time.
Incorporating past exams into your study routine is one of the most effective ways to enhance your exam readiness. By familiarizing yourself with the test format, refining your skills, and improving your time management, you’ll be well-prepared to tackle the real exam with confidence.
Calculators and Tools for the Exam
During exams, having the right tools at your disposal can significantly improve your efficiency and accuracy. Whether it’s a calculator for quick calculations or a set of formulas to reference, using the appropriate resources can help you solve problems more effectively. However, it’s important to know which tools are permitted, how to use them correctly, and how to avoid relying too heavily on them during your preparation.
In this section, we will explore the types of calculators and tools commonly allowed for exams, their advantages, and best practices for using them. Understanding when and how to use these resources is key to maximizing their benefits while avoiding common pitfalls.
Types of Calculators Allowed
Different exams may allow various types of calculators, each with different functionalities. Familiarize yourself with the specific rules regarding calculator usage for your exam. Below are the two main categories of calculators commonly permitted:
- Basic Calculators: These are simple devices that allow for basic arithmetic operations, such as addition, subtraction, multiplication, and division. They are ideal for quickly performing routine calculations.
- Scientific Calculators: These calculators are more advanced and can perform a range of functions, including trigonometric calculations, logarithms, and exponents. They are suitable for solving more complex equations that require additional mathematical operations.
It’s important to check which type is allowed for your exam and practice using it beforehand to become familiar with its functions.
Other Tools and Resources
In addition to calculators, there are other tools and resources that can support your problem-solving during the exam:
- Formula Sheets: Some exams provide formula sheets, while others may allow you to bring your own. These sheets typically include key equations and constants that are commonly used in problem-solving. Make sure to review the formula sheet before the exam and understand how to use it effectively.
- Graphing Tools: For exams that include graphing questions, a graphing calculator or paper may be allowed. Practice plotting equations and interpreting graphs ahead of time so that you can use these resources efficiently during the test.
- Online Resources: If permitted, online resources such as math-solving websites or apps can help clarify difficult concepts. However, always check the exam’s specific guidelines regarding their use.
While tools can certainly make calculations easier, it’s essential to remember that they should support your understanding, not replace it. Practice solving problems manually to strengthen your conceptual knowledge and ensure that you’re not overly dependent on calculators or other resources during the test.
How to Manage Your Time Effectively

Effective time management is one of the key factors in achieving success during any test. Being able to allocate your time wisely ensures that you can complete all sections, check your work, and still feel confident in your answers. Without a plan, you may end up rushing through questions or spending too much time on challenging problems, leaving little time for others. This section will provide strategies to help you manage your time during exams efficiently and reduce stress.
Plan Ahead
Before starting the exam, take a moment to review the entire test. Understand how many questions are in each section, their point values, and how much time you have in total. This will allow you to divide your time in a way that reflects the importance of each section.
- Read Through the Exam: Start by skimming through the test to get a sense of the questions and their difficulty. This will help you identify which sections will take more time and which ones you can quickly answer.
- Allocate Time Wisely: Divide the total time by the number of questions, but adjust based on the complexity of each section. For example, spend more time on multi-step problems and less on simple calculations.
During the Exam
Once you begin the exam, stay focused and stick to the time limits you’ve set for yourself. It’s important not to linger too long on any one question, especially if it’s causing frustration.
- Use a Timer: If allowed, use a watch or a timer to track your progress. Set an alarm to remind you when it’s time to move on to the next section or question.
- Prioritize Easy Questions: Start with the questions you find easiest. This builds confidence and allows you to secure quick points before tackling the more challenging problems.
- Mark Difficult Questions: If you get stuck on a question, mark it and move on. Come back to it later with a fresh perspective if time allows.
By following these strategies, you’ll be able to manage your time more effectively, ensuring that you can complete the entire exam with enough time to double-check your answers and address any remaining questions.
Understanding Common Algebra 2 Concepts
To succeed in any advanced mathematical exam, it’s essential to grasp the key concepts that frequently appear in the test. Understanding these fundamental ideas forms the foundation for solving complex problems with confidence. In this section, we will explore some of the most common mathematical principles that often challenge students and are critical to exam success. By mastering these concepts, you can approach problems with a clearer mindset and reduce the risk of mistakes.
One of the best ways to prepare for the test is to focus on the core topics that tend to appear most often. Whether it’s solving equations, interpreting functions, or working with polynomials, a deep understanding of these concepts will give you an advantage. Let’s take a look at some of the most important concepts you should be familiar with.
- Functions and Graphing: A clear understanding of how to interpret and graph different types of functions–whether linear, quadratic, or exponential–is essential. Recognizing the shape of the graph, as well as understanding domain, range, and intercepts, will help you solve problems efficiently.
- Equations and Inequalities: Mastering the techniques for solving various types of equations and inequalities is crucial. This includes linear, quadratic, and rational expressions, as well as applying methods like factoring, completing the square, and using the quadratic formula.
- Polynomials: Knowing how to simplify, multiply, and factor polynomials is an important skill. Additionally, understanding the behavior of polynomial functions–such as finding zeros and using the Remainder Theorem–will help you solve related problems more effectively.
- Systems of Equations: Being able to solve systems using different methods (substitution, elimination, or matrix operations) is essential. Systems can involve linear and nonlinear equations, and the ability to solve them will be a key part of many exam questions.
- Sequences and Series: Sequences and series often appear in more advanced problems. Understanding how to work with arithmetic and geometric sequences, as well as finding sums and terms, is critical for solving these questions.
These core concepts are not only foundational for the exam but also serve as the building blocks for more advanced topics. Mastering them through practice and understanding will allow you to approach even the most complex problems with confidence and accuracy.
Resources for Algebra 2 Preparation
When preparing for any advanced mathematics exam, using the right study materials and resources can make a significant difference in your performance. From textbooks to online platforms, there are various tools available to help reinforce your understanding of key concepts and improve your problem-solving skills. This section will introduce you to some of the best resources that you can use to prepare effectively for your upcoming test.
It’s important to approach your study plan with a combination of theoretical knowledge and practical exercises. The following resources will provide a well-rounded preparation strategy, including both structured lessons and practice problems.
Online Platforms and Websites

Several online platforms offer free or paid resources designed to help you strengthen your skills. These websites include interactive lessons, practice tests, and tutorials on difficult topics. Below are a few popular websites:
- Khan Academy: A comprehensive resource that covers a wide range of topics, offering video tutorials and practice exercises to reinforce concepts.
- IXL Learning: An online learning platform that provides personalized practice problems, feedback, and progress tracking.
- PatrickJMT: A website with video tutorials on specific math topics, breaking down complex problems step by step.
- Desmos: A graphing calculator tool that helps visualize mathematical functions and explore different types of problems in real-time.
Books and Textbooks

Traditional textbooks and study guides are essential for in-depth learning and exam preparation. These resources provide explanations, examples, and practice exercises to solidify your understanding. Consider using the following books:
- “Precalculus: Mathematics for Calculus” by Stewart, Redlin, and Watson: This textbook covers foundational topics needed for advanced math courses and exams, including functions and graphing.
- “The Art of Problem Solving: Introduction to Algebra” by Richard Rusczyk: A great book for building problem-solving skills and mastering the basics.
- “Barron’s Test Prep: High School Math”: This study guide is designed specifically for standardized math exams, with tips, strategies, and practice tests.
Practice Tests and Problem Sets

Regular practice is critical to performing well in any exam. Below is a table outlining some resources that offer practice tests and problem sets tailored to your needs:
| Resource | Type of Material | Key Feature |
|---|---|---|
| Old Exam Papers | Practice Tests | Real-world test experience, helpful for timing yourself |
| Study.com | Practice Problems | Comprehensive topic-wise quizzes |
| Mathway | Problem Solver | Instant step-by-step solutions to practice problems |
Using these resources in combination with consistent study habits will significantly boost your confidence and preparedness for the test. By focusing on your weak areas, practicing regularly, and testing yourself under exam conditions, you will be well on your way to success.
How to Review Mistakes and Improve
One of the most effective ways to improve in any subject is by learning from your mistakes. Reviewing errors is an essential part of the learning process, as it helps you understand where you went wrong and prevents similar mistakes in the future. In this section, we will explore how to systematically review your errors and turn them into valuable learning opportunities.
When it comes to improving your problem-solving skills, simply correcting your mistakes is not enough. It’s important to analyze why the mistake occurred and how you can avoid it in the future. This reflective process will not only boost your confidence but also help you build a deeper understanding of the material.
Step 1: Identify the Root Cause of Mistakes

After completing a practice test or set of problems, it’s crucial to go back and look at the mistakes you made. Rather than just noting the correct answer, take the time to examine why the error happened. Ask yourself the following questions:
- Did I misunderstand the question? Sometimes, confusion arises from misinterpreting the problem’s instructions or wording.
- Did I make a calculation error? Double-check your arithmetic or algebraic manipulations. Even small mistakes can lead to incorrect answers.
- Was I unclear on the method or concept? If a particular concept or formula seemed difficult, revisit it and review the steps involved.
- Was I rushing or under pressure? Stress or time constraints can often lead to careless mistakes. Make sure to pace yourself appropriately during practice.
Step 2: Correct the Mistakes and Understand the Concept
Once you’ve identified the cause of the mistake, the next step is to correct it. It’s important to go beyond just finding the right answer–take the time to fully understand the correct method. This may involve:
- Re-reading your textbook or notes: Sometimes, the solution to the problem is hidden in a concept that you haven’t fully grasped. Revisiting the relevant section can provide clarity.
- Watching instructional videos: Online resources like YouTube or Khan Academy offer visual explanations of difficult concepts that might help reinforce your understanding.
- Doing additional practice problems: Practice makes perfect. By solving similar problems, you can reinforce the correct methods and ensure that you don’t make the same mistakes again.
Step 3: Track Your Progress and Stay Consistent
Keeping track of the mistakes you’ve made and how you’ve addressed them is essential for continuous improvement. Maintain a log of the problems you’ve encountered, including what went wrong and how you corrected it. This can be in the form of a simple notebook or a digital document.
Consistency is key to improvement. Regularly review your errors and continue practicing. The more mistakes you make and learn from, the better prepared you’ll be for the real test.
By taking the time to thoroughly review your mistakes and applying the right strategies for improvement, you will gradually build a deeper understanding of the material. Remember, errors are not failures–they are simply opportunities for growth and mastery.
Final Tips for the Upcoming Exam
As the exam day approaches, it’s crucial to refine your study strategies and make sure you’re fully prepared. This final phase of preparation is about fine-tuning your approach, managing any remaining uncertainties, and building confidence. The last few days before the test should focus on reinforcing what you’ve learned and avoiding common pitfalls that could affect your performance.
In this section, we’ll share practical advice on how to make the most of your remaining study time, avoid last-minute stress, and stay mentally sharp during the exam. These tips will help you approach the test with a calm and focused mindset, giving you the best chance to succeed.
Stay Focused During the Last Week
In the final week leading up to the exam, your focus should be on review and consolidation rather than learning new material. Follow these steps to maximize your last-minute study sessions:
- Prioritize weak areas: Focus on concepts or problem types that you find most challenging. Spend extra time on areas where you’ve made the most mistakes in practice tests.
- Review key formulas and concepts: Ensure you have a solid understanding of the essential formulas and methods that frequently appear on the exam.
- Take short, focused study sessions: Avoid long, tiring study marathons. Aim for 1-2 hour blocks with breaks in between to maintain concentration.
Get Plenty of Rest Before the Test
The importance of rest cannot be overstated. In the days before the exam, ensure you’re getting enough sleep to be mentally and physically refreshed. Lack of sleep can hinder your ability to think clearly and solve problems effectively. Aim for at least 7-8 hours of sleep the night before the exam to ensure optimal brain function on the day of the test.
Practice Under Timed Conditions
To simulate the pressure of the actual exam, try practicing problems under timed conditions. This will help you get used to the pace you need to maintain throughout the test. You can use practice exams, or set a timer when working through problems from your study materials. This will also help you learn how to allocate time to different sections without rushing.
Review Test-Taking Strategies
In addition to reviewing content, make sure you have a solid test-taking strategy. Keep the following in mind:
- Read the instructions carefully: Always take the time to read each question carefully, ensuring you understand exactly what is being asked before answering.
- Start with the easiest questions: Answer the questions you know well first. This will boost your confidence and ensure you don’t waste time on difficult questions right away.
- Manage your time: Keep track of the time during the exam to ensure you complete all sections. If you get stuck on a question, move on and come back to it later if time permits.
By following these final tips and keeping a calm, focused mindset, you will be well-prepared for the exam. Remember that preparation is not just about hard work but also about managing your mental and physical well-being. Good luck!