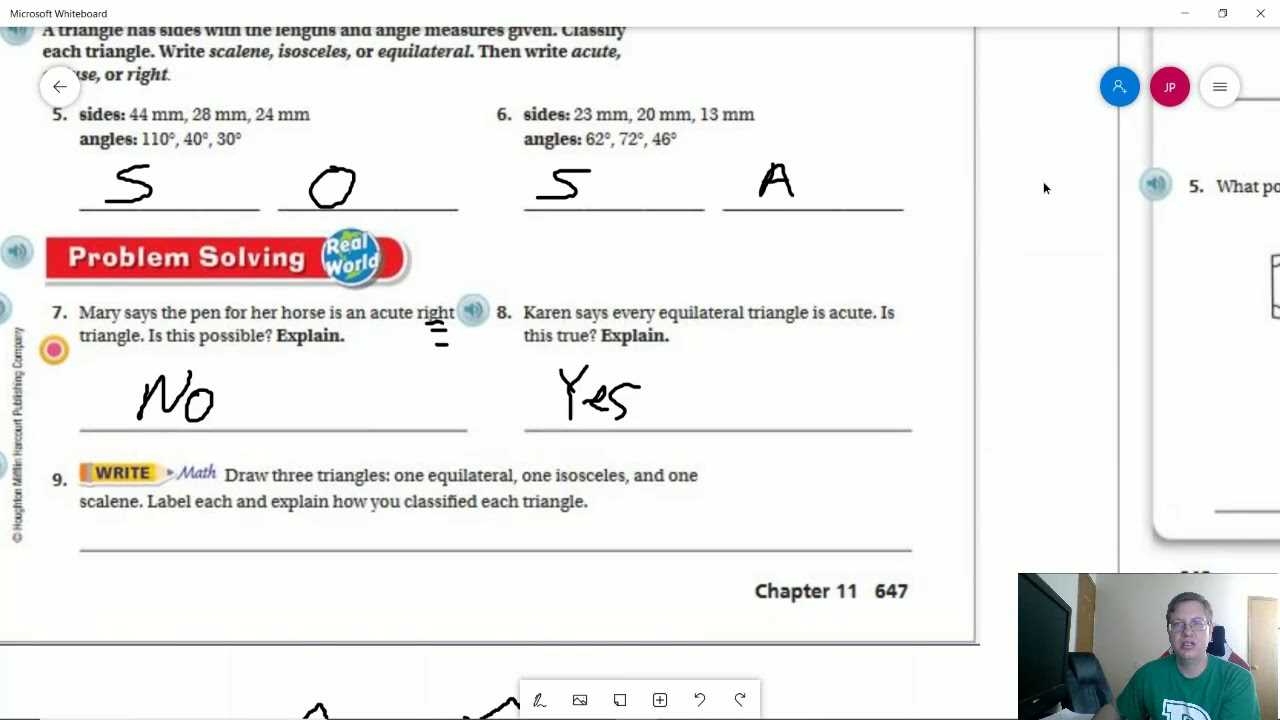
In this guide, we will explore essential techniques and methods that help break down complex mathematical topics into simpler, manageable steps. This approach is designed to improve comprehension and provide clarity for students at different levels of learning.
Whether you’re tackling word problems, equations, or formulas, the focus is on providing clear, actionable solutions that guide you through each challenge. Mastering these skills will build a solid foundation for solving more advanced problems with confidence.
By following structured examples and practicing with real-world scenarios, you’ll develop a deeper understanding and improve both speed and accuracy. It’s all about honing your problem-solving abilities and strengthening your overall approach to studying mathematics effectively.
Go Math Lesson 11.3 Answers
This section provides detailed solutions and explanations for various problems, aimed at enhancing understanding and reinforcing key concepts. By breaking down each step clearly, we help make complex topics more accessible for learners of all levels.
Throughout this guide, you’ll find examples that demonstrate how to approach different types of problems. Each solution is designed to illustrate the thought process and reasoning behind each step, helping you to develop problem-solving skills and confidence.
Here are some of the key strategies covered:
- Identifying and applying core principles effectively
- Breaking down multi-step problems into simpler tasks
- Using visual aids and diagrams for clarity
- Practice exercises to strengthen understanding
By following the examples provided, you can gain a deeper understanding of how to solve problems more efficiently. This approach also helps you become familiar with different types of challenges and methods that can be used to tackle them.
In the following sections, we’ll go over specific problems and the most effective ways to solve them. Each example is carefully crafted to showcase the necessary steps, so you can apply the techniques learned to similar problems in the future.
Understanding Key Concepts in Lesson 11.3
This section focuses on grasping the foundational ideas and methods that serve as the backbone of problem-solving in this unit. By thoroughly understanding these concepts, you can apply them effectively across various exercises and scenarios. The goal is to develop a clear and structured approach that enhances both understanding and accuracy.
Key topics explored include identifying core principles, recognizing patterns, and learning how to apply rules consistently. Mastery of these concepts is essential for tackling more complex tasks and for strengthening your problem-solving skills. By building on these concepts step by step, you gain a deeper insight into the material, improving your overall performance.
Step-by-Step Solutions for Go Math
This section provides a structured breakdown of various problems, guiding you through each step necessary to arrive at the correct solution. By following the detailed process, you can learn to approach similar challenges with confidence and clarity.
Each example is designed to highlight the key stages of problem-solving, from understanding the question to applying the correct strategies. The goal is to make each step understandable, so you can replicate the approach independently.
Here’s how the process works:
- Identify the core problem: Carefully read through the question to understand what is being asked.
- Break the problem into smaller parts: Divide complex tasks into manageable sections.
- Choose the right method: Select the appropriate technique or formula based on the given information.
- Execute the solution: Apply the chosen method step by step to solve the problem.
- Verify the result: Double-check the calculations to ensure accuracy and correctness.
By following this approach, you can systematically solve problems while reinforcing your understanding of the underlying principles. Each step is designed to build your problem-solving skills and improve your ability to tackle future exercises with greater ease.
Common Mistakes in Lesson 11.3
While working through exercises, it’s easy to make certain mistakes that can lead to confusion or incorrect solutions. Recognizing and avoiding these errors is essential for improving accuracy and understanding. In this section, we will highlight the most common pitfalls and how to avoid them.
Misunderstanding the Problem
One frequent mistake is not fully understanding the problem before attempting to solve it. Skimming through the question or overlooking key details can result in applying the wrong method. To avoid this, take time to carefully read and analyze the problem, identifying what is being asked before proceeding with the solution.
Skipping Key Steps

Another common error is skipping intermediate steps in the problem-solving process. This often happens when students rush to the answer without following the necessary steps, leading to mistakes or incomplete solutions. To ensure accuracy, follow each step methodically and check that all calculations are done correctly.
By being aware of these common mistakes, you can develop a more precise approach to solving problems and avoid setbacks that might hinder your progress. Practice and attention to detail will help in mastering the material efficiently.
Tips for Mastering Go Math 11.3
Mastering complex problems requires not just understanding the individual steps but also developing effective strategies for consistent practice and application. In this section, we’ll outline essential tips that will help improve your problem-solving skills and lead to better results.
| Tip | Description |
|---|---|
| Understand Key Concepts | Focus on the foundational principles and ensure you understand their application before moving on to more complex problems. |
| Break Down Problems | Divide larger, multi-step problems into smaller, more manageable tasks to avoid feeling overwhelmed. |
| Practice Regularly | Consistent practice reinforces concepts and improves familiarity with different problem types. |
| Review Mistakes | After solving problems, carefully review mistakes to understand where and why errors occurred, which helps avoid repeating them. |
| Seek Clarification | If something is unclear, don’t hesitate to ask for help or look for additional resources that explain difficult concepts in more detail. |
By following these tips, you’ll not only improve your problem-solving techniques but also gain a deeper understanding of the material, ensuring greater success in tackling similar challenges in the future.
How to Solve Word Problems in 11.3

Word problems can be one of the most challenging aspects of any subject, as they require not only understanding the concepts but also translating them into solvable steps. Here’s a systematic approach to help you tackle these problems effectively and with confidence.
To solve word problems, follow these essential steps:
- Read the problem carefully: Understand all the information provided. Highlight or underline key facts and numbers.
- Identify the question: Clearly determine what is being asked in the problem. This helps focus on the end goal.
- Break it down into smaller steps: Separate the problem into manageable parts, and solve each step systematically.
- Choose the correct approach: Based on the information, decide which method or formula to use.
- Perform the calculations: Carefully carry out each step, checking your work as you go along.
- Verify the solution: Once you’ve solved the problem, review the result to ensure it makes sense in the context of the question.
By following this method, you can approach word problems with a clear strategy, reducing confusion and increasing your accuracy. Practice with different examples will help solidify these steps and improve your problem-solving skills over time.
Explanation of Go Math 11.3 Strategies

In this section, we will explore the key strategies that are essential for solving problems effectively and efficiently. These approaches help simplify complex tasks and ensure that the right methods are applied at each step. Understanding and mastering these strategies will significantly improve problem-solving skills and boost overall performance.
Breaking Down Complex Problems
One of the most effective strategies is to break down complicated problems into smaller, more manageable parts. By isolating each element, you can focus on solving one step at a time, which makes the entire process less overwhelming. This approach also helps to avoid mistakes that can occur when trying to solve everything at once.
Using Visual Aids for Better Understanding
Another valuable strategy is to use visual aids, such as diagrams or charts, to better understand the relationships between different parts of a problem. Visual representations make abstract concepts clearer and provide a roadmap for solving the problem step by step. This method is especially helpful when dealing with geometric or data-related questions.
By applying these strategies, you’ll develop a more organized approach to solving problems. With practice, you’ll find that these methods not only make difficult tasks easier but also increase your confidence in tackling new challenges.
Help with Practice Problems in 11.3
Practicing with problems is essential for mastering new concepts and improving problem-solving skills. In this section, we will guide you through the process of solving practice problems, offering tips and strategies to help you approach them with confidence and clarity. Whether you’re just starting or need extra assistance, this guide will provide the support you need.
Breaking Down Practice Problems
The first step in tackling practice problems is to break them into smaller, manageable steps. By focusing on each part individually, you can ensure that you’re addressing the core elements of the question and not getting overwhelmed. Start by identifying the information provided, and then carefully determine what is being asked before selecting the appropriate method.
Working Through Sample Problems
Working through sample problems is an excellent way to practice and reinforce your understanding. For each example, follow the same steps you would in a real problem: read the question, break it down, apply the correct method, and double-check your solution. With repeated practice, these steps will become second nature, and you’ll be able to solve problems more efficiently.
By following these steps and practicing consistently, you’ll strengthen your problem-solving abilities and gain confidence in applying what you’ve learned. Practice is key to becoming proficient, so make sure to work through as many examples as possible.
Visual Aids for Go Math Answers
Visual tools are powerful aids that can enhance understanding and simplify complex problems. By using diagrams, charts, or other forms of visual representation, you can more easily grasp the relationships between different elements in a problem and solve it step by step. In this section, we will discuss how to effectively use visual aids to support your learning and problem-solving process.
Using Diagrams for Clarity
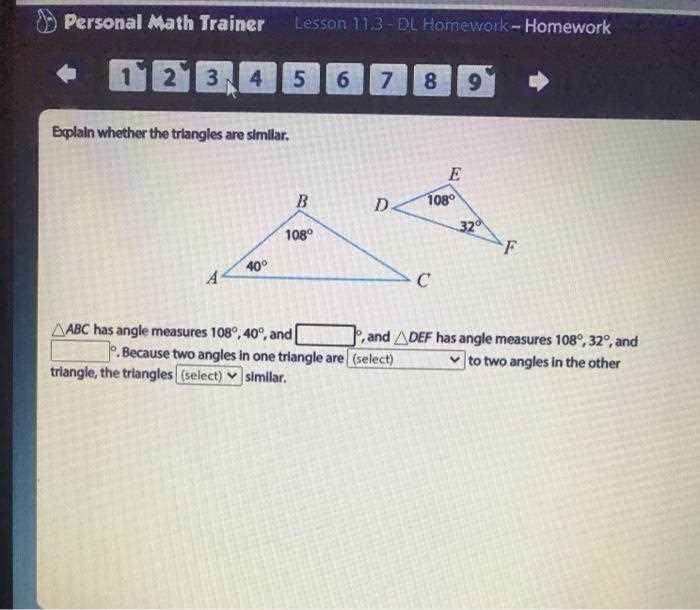
Diagrams are particularly useful when dealing with problems that involve spatial reasoning or geometric concepts. Drawing out the elements of a problem helps visualize how different components interact with each other. Whether it’s a shape, a graph, or a number line, creating a visual representation can make abstract ideas much clearer and easier to work with.
Utilizing Charts and Tables
Charts and tables are excellent for organizing data and comparing different values. When dealing with problems that require calculations or require you to track multiple pieces of information, creating a table can help you stay organized and avoid confusion. These tools also make it easier to spot patterns and trends, which can lead to faster and more accurate solutions.
Incorporating visual aids into your study routine can significantly improve both your understanding and retention of key concepts. By practicing with diagrams, charts, and other visual tools, you’ll develop stronger problem-solving skills and a more intuitive grasp of the material.
Go Math 11.3 Homework Assistance
Completing assignments can sometimes be challenging, especially when faced with complex problems. This section provides valuable tips and strategies to help you navigate through homework tasks with ease. Whether you’re struggling with understanding a particular concept or simply need guidance on how to approach problems, these steps will offer the support you need.
Here are some helpful tips for tackling homework problems:
- Review Class Notes: Before starting, review your notes to refresh your memory on key concepts and problem-solving methods discussed in class.
- Identify Key Information: Carefully read through the problem to identify the key facts and what is being asked. Highlight or underline important details.
- Break Problems into Smaller Steps: If a problem feels overwhelming, divide it into smaller, manageable parts. Solve each part individually and then combine your results.
- Work Through Examples: Look for similar examples in your textbook or notes. These can serve as a guide and show you how to approach similar problems.
- Use Online Resources: If you’re still stuck, consider using reliable educational websites or videos for additional explanations.
- Ask for Help: Don’t hesitate to ask your teacher, tutor, or a classmate for assistance if you’re having difficulty understanding the material.
By following these tips, you’ll build confidence and improve your ability to complete assignments more efficiently. Remember, practice is key, and with time, the process will become more intuitive.
How to Check Your Answers Correctly
Checking your solutions is a crucial step in the problem-solving process. It ensures that you’ve followed the correct methods and arrived at the right results. In this section, we will explore effective techniques for reviewing your work, identifying errors, and confirming the accuracy of your answers.
To check your work effectively, follow these strategies:
- Review Each Step: Go through the solution process step by step. Ensure that you applied the correct methods and followed all necessary calculations without skipping any details.
- Estimate the Answer: Before diving into detailed checking, estimate the expected outcome. This helps you quickly identify any major discrepancies in your solution.
- Double-Check Calculations: Revisit any calculations or operations. Small errors in addition, subtraction, multiplication, or division can lead to incorrect results.
- Use a Different Method: If possible, try solving the problem using a different approach or formula to see if you get the same answer.
- Check Units and Labels: Ensure that your final answer has the correct units and labels, especially if the problem involves measurements or quantities.
- Seek External Confirmation: Use available resources, such as answer keys or online tools, to verify your final answer. Cross-checking with trusted sources can provide additional confidence in your results.
By following these steps, you can develop a habit of thoroughly reviewing your work, which will help improve your accuracy and build stronger problem-solving skills.
Quick Review of Lesson 11.3 Topics
This section provides a concise overview of the key concepts covered, helping reinforce your understanding and clarify any doubts. A quick review can help solidify the knowledge and prepare you for more advanced topics. Let’s recap the main points to ensure you are comfortable with the material.
Core Concepts Explored
In this section, we explored several important ideas, including the fundamentals of how to approach complex problems step by step. The focus was on building a solid foundation that allows you to tackle similar challenges with confidence. Key techniques, such as breaking down problems into smaller, more manageable parts, were introduced to enhance problem-solving skills.
Essential Strategies for Success
We also discussed effective strategies to improve your performance, such as reviewing key formulas, understanding the process of working through examples, and identifying patterns that can simplify calculations. Remember that practice plays a significant role in mastering these techniques, and the more you apply them, the more intuitive they become.
By revisiting these essential concepts and methods, you’ll reinforce your skills and be better equipped to solve problems with greater efficiency and accuracy.
Understanding the Formulas Used
Formulas are essential tools for solving various problems efficiently. Understanding how they work and how to apply them correctly is key to solving challenges effectively. In this section, we will break down the most commonly used formulas and explain how each one serves a specific purpose in problem-solving scenarios.
Here are some key formulas and their uses:
| Formula | Description | Example |
|---|---|---|
| Area of a Rectangle | Used to calculate the area inside a rectangle. Multiply the length by the width. | Area = Length × Width |
| Perimeter of a Rectangle | Used to calculate the total distance around a rectangle. Add the lengths of all four sides. | Perimeter = 2(Length + Width) |
| Volume of a Rectangular Prism | Used to find the space inside a rectangular prism (box). Multiply the length, width, and height. | Volume = Length × Width × Height |
By understanding how each formula works and when to apply it, you’ll be able to solve a variety of problems more effectively. Remember, knowing the right formula for a specific situation is a crucial step in reaching the correct solution.
Improving Your Accuracy with 11.3
Precision is essential when working through complex problems. Even small mistakes can lead to incorrect results. In this section, we will focus on strategies that can help you improve your accuracy and avoid common errors. By refining your approach, you can achieve better outcomes and gain confidence in your problem-solving skills.
Key Tips to Enhance Accuracy

Here are several practical strategies you can apply to ensure accuracy while solving problems:
- Double-check calculations: After performing calculations, always go back and verify each step. This helps catch any small errors that may have been overlooked.
- Work step-by-step: Break down each problem into smaller parts. This makes it easier to identify mistakes early and ensures that each step is correct before moving on to the next.
- Use estimation: Before solving a problem, estimate the answer. If your final result is far off from your estimate, it’s a good indication that something went wrong.
- Understand the concepts: A strong grasp of the underlying principles will help you avoid common errors that arise from misunderstanding the problem.
- Review your work: Always review your work at the end. A quick check can often reveal mistakes that are easy to miss in the heat of solving a problem.
Common Pitfalls to Avoid
Being aware of common mistakes is just as important as applying strategies for accuracy. Some errors you might encounter include:
- Rushing through the steps without paying attention to details.
- Misreading the problem or misunderstanding key information.
- Skipping over intermediate steps, which can lead to skipped calculations.
By staying focused and applying these strategies, you will improve your accuracy and develop stronger problem-solving habits. Practice and careful attention to detail are key to achieving better results.
Practice Questions for Lesson 11.3
To solidify your understanding of the concepts, it’s crucial to engage with a variety of practice problems. These exercises will help reinforce your skills and provide the opportunity to apply what you’ve learned. Below are some practice questions designed to challenge your knowledge and improve your problem-solving abilities.
Sample Practice Problems
Try solving the following questions. After completing them, check your work to ensure you’ve understood the material thoroughly.
| Problem | Instructions |
|---|---|
| Problem 1 | Solve the equation for x: 4x + 5 = 21 |
| Problem 2 | Find the area of a rectangle with a length of 12 cm and width of 8 cm. |
| Problem 3 | Determine the value of y in the expression: 3y – 9 = 18 |
| Problem 4 | What is the perimeter of a square with a side length of 5 meters? |
Answer Verification
Once you have completed the problems, verify your answers by reviewing the solution strategies. This will ensure that you’re able to solve similar questions with confidence in the future.
Go Math 11.3 Solutions for Parents
Supporting your child’s learning is essential in helping them grasp challenging concepts. As a parent, understanding the strategies and methods used in their studies can make a significant difference in their academic progress. This section offers guidance and resources to help you assist your child with their homework and improve their problem-solving skills.
Here are some tips and strategies for parents to help their children succeed:
- Encourage Independent Problem-Solving: Allow your child to work through problems on their own, offering guidance when needed but letting them take the lead.
- Clarify Instructions: Help your child read and understand the questions, breaking them down into smaller, more manageable steps if necessary.
- Provide Visual Aids: Use diagrams, charts, or other visual tools to help your child better understand abstract concepts.
- Use Real-World Examples: Show how the problems relate to everyday situations to make the concepts more tangible.
- Be Patient: Some students may need more time to understand the material. Offer positive reinforcement and be patient as they work through each challenge.
By utilizing these strategies, you can offer valuable support to your child and foster a positive learning environment at home.
Key Takeaways from Lesson 11.3
Understanding key concepts and applying strategies effectively is crucial for mastering any subject. This section highlights the most important takeaways from this part of the curriculum, offering a concise review of the core ideas that students should grasp. By focusing on these main points, learners can strengthen their foundational knowledge and improve their ability to solve related problems independently.
Key concepts to remember include:
- Core Principles: The fundamental techniques and approaches that underpin the problems tackled in this section.
- Problem-Solving Strategies: How to break down complex problems into smaller, manageable parts for easier understanding and solution.
- Application of Formulas: Knowing when and how to apply the relevant formulas to arrive at correct solutions.
- Common Pitfalls: Identifying and avoiding the common mistakes that can arise when solving problems, and how to overcome them.
By mastering these core elements, students will be well-equipped to handle future challenges and build confidence in their abilities.
Preparing for Tests with Go Math 11.3
When preparing for exams, it’s essential to focus on understanding the key concepts, mastering problem-solving techniques, and reviewing important topics that frequently appear in assessments. This section provides a guide on how to effectively prepare for tests by revisiting the most critical elements covered in the curriculum. A well-structured study plan will help reinforce your knowledge and boost confidence when facing any evaluation.
Here are some practical tips to ensure you’re ready:
- Review Key Concepts: Focus on the fundamental principles taught in this section. Understanding the core ideas is essential for tackling complex problems.
- Practice Problems: Solve various problems from the workbook and online resources. The more practice you do, the better you’ll understand the material.
- Use Study Guides: Utilize available study guides and practice tests to simulate the test environment and identify areas where you need improvement.
- Group Study: Collaborate with classmates to discuss challenging problems. Explaining concepts to others can deepen your understanding.
Additionally, here’s a quick review of some essential topics:
| Topic | Focus Area |
|---|---|
| Core Principles | Understand foundational methods used in problem-solving. |
| Key Formulas | Practice applying relevant formulas correctly in various scenarios. |
| Common Mistakes | Identify typical errors and learn how to avoid them. |
| Problem-Solving Strategies | Break problems into smaller, manageable steps for easier solutions. |
By following these steps and dedicating time to study, you’ll be well-prepared to tackle any test with confidence.