
Preparing for advanced mathematics assessments requires both a solid understanding of key concepts and the ability to apply them under timed conditions. This section focuses on strategies and resources to help students tackle complex problems effectively, offering valuable insights into the types of questions commonly encountered.
Through a thorough review of past problems and solutions, students can gain a deeper understanding of the problem-solving techniques necessary for success. In addition, practicing these problems regularly can help improve speed and accuracy, essential for achieving a high score. Emphasis is placed on interpreting questions correctly and executing the appropriate mathematical methods with confidence.
2012 AP Calculus BC Exam Multiple Choice Answers
This section delves into the correct solutions for the key questions found in the AP advanced mathematics assessment. By analyzing the problems from a strategic perspective, students can learn how to approach complex scenarios and apply the appropriate techniques for solving them efficiently.
The focus is on understanding the underlying concepts behind each question, recognizing common patterns, and learning the best methods for reaching the correct conclusions. This approach not only helps clarify the reasoning behind each solution but also enhances problem-solving skills for future assessments.
Overview of AP Calculus BC Exam

The AP advanced mathematics test is designed to assess students’ proficiency in higher-level mathematical concepts, emphasizing their ability to solve complex problems and apply theoretical knowledge in practical contexts. The assessment covers a broad range of topics, providing a comprehensive challenge for students who seek to demonstrate their skills and understanding of the subject.
This test includes a variety of problem types, ranging from theoretical questions to real-world applications, all of which require careful analysis and strong problem-solving abilities. A key component of the test is the ability to manage time effectively while tackling intricate and multi-step problems.
| Topic | Description |
|---|---|
| Limits and Continuity | Understanding the behavior of functions as they approach specific values. |
| Differentiation | Applying techniques of finding rates of change and slopes of curves. |
| Integration | Using integrals to find areas under curves and solve real-world problems. |
| Series and Sequences | Analyzing infinite series and understanding their convergence properties. |
| Polar Coordinates | Exploring coordinate systems for representing curves and calculating areas. |
How to Approach Multiple Choice Questions
When faced with a series of problem-solving tasks, it’s essential to develop an effective strategy for tackling each question efficiently. With a well-thought-out approach, students can save time and reduce errors while working through various types of questions.
Here are some helpful steps to follow when approaching these tasks:
- Read the Question Carefully: Take the time to fully understand the problem before jumping into calculations. Often, key details can be hidden within the wording.
- Identify Known Information: Determine which pieces of information are given and how they relate to the question at hand.
- Eliminate Obvious Incorrect Options: Cross out answers that are clearly wrong. This will increase your chances if you need to guess.
- Work Step-by-Step: Break down the problem into manageable parts. Focus on one calculation or concept at a time to avoid feeling overwhelmed.
- Use Approximation When Necessary: If you’re unsure about an exact answer, estimate values or use logical reasoning to guide your decision.
By following these strategies, you can improve your chances of correctly solving problems in a timely manner while avoiding common pitfalls.
Key Topics Covered in 2012 Exam
The test assesses a wide range of advanced mathematical concepts, requiring students to demonstrate their understanding and ability to apply these principles effectively. The questions cover both foundational topics and more complex theories, designed to challenge and evaluate critical thinking and problem-solving skills.
Some of the key topics included in the assessment are:
- Limits and Continuity: Exploring the behavior of functions at specific points and over intervals, and understanding concepts like continuity and discontinuities.
- Differentiation: Techniques for finding the rates of change of functions, including rules such as the product, quotient, and chain rules.
- Integration: Applying integrals to solve problems related to areas under curves, volumes, and other real-world applications.
- Series and Sequences: Investigating infinite series, their convergence, and applying tests like the ratio test and integral test.
- Polar Coordinates and Parametric Equations: Understanding the representation of curves and solving problems in alternative coordinate systems.
- Vector Calculus: Applying vector operations to solve problems in three-dimensional space, including concepts like dot products and cross products.
Mastery of these topics is essential for success, and a clear understanding of their applications is necessary for solving complex problems efficiently and accurately.
Common Mistakes to Avoid in Calculus BC
When preparing for advanced mathematics assessments, students often fall into several common traps that can hinder their performance. These mistakes range from simple computational errors to misunderstandings of key concepts, and they can significantly impact the accuracy of solutions. By recognizing these pitfalls in advance, students can better equip themselves to avoid them and improve their problem-solving strategies.
Misunderstanding Question Requirements
One of the most frequent errors is misinterpreting what a question is asking. This can lead to applying the wrong method or overlooking important information. Always read the problem carefully and identify what is being requested before attempting to solve it. Pay attention to terms such as “exact value” versus “approximate value,” or “find the slope” versus “find the area under the curve.” Clear comprehension of the task is crucial.
Neglecting to Simplify Expressions
Students often skip crucial steps when simplifying expressions, which can lead to incorrect results. Whether it’s failing to factor an equation, skipping the necessary algebraic manipulation, or overlooking simplifications in integrals or derivatives, these shortcuts can cause small but significant errors. Ensure every step is fully worked out and that final expressions are simplified before moving on to the next part of the problem.
By avoiding these common mistakes and practicing careful analysis, students can enhance their accuracy and improve their overall performance in advanced mathematical assessments.
Tips for Efficient Exam Preparation
Effective preparation is key to success in advanced mathematics assessments. By following a strategic approach, students can maximize their study time, strengthen their understanding of critical concepts, and improve their problem-solving skills. Proper planning and consistent practice are essential for mastering complex topics and performing well under pressure.
Establish a Structured Study Schedule
One of the best ways to stay organized is by creating a study plan that allocates enough time for each topic. Break down the material into manageable sections and set realistic goals for each study session. Be sure to include review time for earlier topics to reinforce what you’ve already learned and avoid last-minute cramming.
Focus on Practice and Review

Regular practice is crucial for improving problem-solving speed and accuracy. Solve as many practice problems as possible, especially those that challenge your weak areas. After completing each problem, carefully review your solutions to identify any mistakes and understand the reasoning behind each step. This will deepen your understanding and help avoid common errors during the test.
Strategies for Solving Complex Problems

Approaching difficult mathematical problems requires both analytical thinking and the ability to break down complicated concepts into simpler steps. The best strategy is to stay methodical and patient, ensuring that every detail is addressed. With the right techniques, even the most challenging questions can be solved efficiently.
Here are some strategies to help you tackle complex problems effectively:
- Break the Problem Into Smaller Parts: Divide the question into manageable sections. Solving smaller parts one at a time makes the overall problem less overwhelming.
- Look for Patterns or Symmetry: Many complex problems have underlying patterns. Identifying these can simplify calculations and help recognize shortcuts.
- Use Approximations When Appropriate: For certain problems, estimating values or using approximations can guide you toward the correct solution, especially when an exact answer is not necessary.
- Check for Hidden Information: Carefully examine the problem for any hidden variables or extra details that may not be immediately obvious but are essential for solving it.
- Work Backwards: If you’re stuck, sometimes solving the problem backwards or starting from the conclusion can help reveal the necessary steps.
By applying these methods, you’ll improve your ability to navigate complex questions and find solutions more efficiently under time constraints.
Understanding the Grading System

To perform well in advanced mathematical assessments, it’s crucial to understand how your performance is evaluated. Grading systems are designed to assess your mastery of key concepts, with each section of the test carrying a specific weight that contributes to your final score. Understanding this structure helps you manage your time and focus on the areas that will impact your grade the most.
How Scores Are Calculated
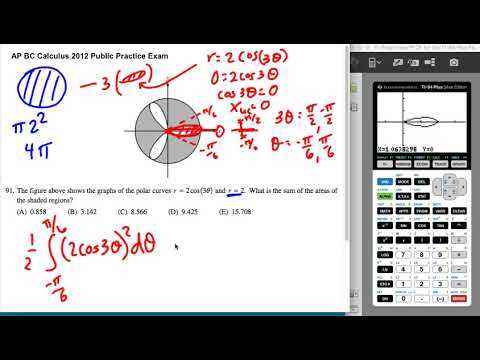
Each problem or section typically receives a set number of points, and your score is determined by the number of correct responses you provide. The final grade is often presented as a scaled score, which is adjusted to reflect the difficulty of the test and ensure fairness across different years and groups of students.
Breakdown of Scoring Components
| Section | Point Allocation | Percentage of Final Score |
|---|---|---|
| Conceptual Understanding | 50-60 points | 40% |
| Problem Solving Skills | 40-50 points | 35% |
| Application of Knowledge | 20-30 points | 25% |
This breakdown helps clarify where to focus your study efforts, ensuring you strengthen both your theoretical knowledge and practical problem-solving ability.
Practice Questions from 2012 Exam
One of the best ways to prepare for any advanced mathematical assessment is through practice. Working through questions from previous tests allows you to familiarize yourself with the types of problems you’ll face, develop your problem-solving strategies, and refine your ability to work under time constraints. By solving a variety of questions, you can identify patterns and improve your overall readiness.
Sample Question 1: Limits and Continuity

Problem: Determine the limit of the function as x approaches 0:
f(x) = (sin x) / x
What is the value of this limit?
Solution: To solve this problem, recall the standard limit result:
lim (sin x) / x = 1 as x approaches 0. Therefore, the limit of the function is 1.
Sample Question 2: Integration Techniques
Problem: Evaluate the integral:
∫ (x^3 – 2x) dx
What is the antiderivative of this function?
Solution: To solve this integral, apply the power rule for integration:
∫ x^n dx = (x^(n+1)) / (n+1) + C
For the given function, the solution is:
∫ (x^3 – 2x) dx = (x^4) / 4 – x^2 + C
These practice questions are designed to challenge your understanding of key concepts and improve your ability to solve problems quickly and accurately. Regular practice with a variety of problems is an effective way to enhance your skills.
Analyzing the Answer Key

After completing a practice set or mock test, it is essential to carefully review the provided solutions to understand why certain responses are correct or incorrect. Analyzing the key not only helps identify mistakes but also enhances your comprehension of the material by revealing the reasoning behind each step. This process is critical for reinforcing concepts and improving your problem-solving approach.
Understanding the Rationale Behind Correct Responses
Each correct solution is based on established mathematical principles and strategies. By studying the solution process, you can uncover the specific techniques used to arrive at the correct result. This might involve applying formulas, manipulating expressions, or recognizing patterns. By internalizing these methods, you can replicate them when faced with similar questions in the future.
Identifying Common Mistakes
Examining the mistakes you made and contrasting them with the correct solutions provides insight into common errors. Often, missteps occur due to overlooked details, rushed calculations, or incorrect assumptions. By recognizing these patterns, you can take steps to avoid making the same errors again, thus improving your accuracy in future tests.
Incorporating this analysis into your study routine can significantly enhance your learning and increase your chances of success. Understanding both the correct solutions and your errors is essential for mastering complex topics and achieving better results over time.
Calculus BC vs AB: Key Differences
When it comes to advanced mathematics courses, there are several levels designed to cater to students’ varying skills and readiness. Understanding the distinctions between these courses is essential for making an informed decision about which one to take. While both levels assess similar core concepts, they differ significantly in depth, scope, and complexity.
Content Scope
The primary difference between the two levels lies in the breadth of topics covered. The more advanced course introduces additional concepts that require a deeper understanding of mathematical theory and application. Below are the key content areas for each course:
- AB Level: Focuses on fundamental principles of differential and integral calculus, including limits, derivatives, integrals, and basic series.
- BC Level: Includes all topics from AB, plus additional material such as polar coordinates, parametric equations, sequences and series, and advanced integration techniques.
Difficulty Level
While both courses challenge students, the more advanced level demands a higher level of mathematical reasoning and problem-solving ability. The extra topics introduced in the BC level require students to grasp more complex ideas and apply them in various contexts.
- AB Level: Geared towards students with a strong grasp of basic calculus concepts and who are comfortable with problem-solving in a more structured manner.
- BC Level: Intended for students who are already proficient in the basic concepts and are ready to handle more challenging and abstract mathematical problems.
Ultimately, the choice between the two depends on the student’s goals, academic strengths, and how much time they are willing to dedicate to mastering more advanced material. Understanding these differences will help ensure the best fit for each student’s needs and aspirations.
Effectively Managing Your Exam Time
Time management is crucial when tackling a rigorous test. Properly allocating your time during the assessment allows you to approach each section with a clear focus and ensures that you complete the test without unnecessary stress. Creating a strategy to manage your time can make a significant difference in your overall performance.
Planning Your Approach
Before diving into the test, take a moment to quickly assess the structure and number of questions. This will help you estimate how much time to spend on each section. Having a strategy before starting can prevent you from spending too much time on any one part and ensures a balanced distribution of your effort throughout the test.
- Read Through the Instructions: Ensure you understand the directions for each section before starting to avoid confusion later.
- Set Time Limits for Each Section: Allocate a specific amount of time to each part of the test based on its difficulty and length.
- Prioritize Easier Questions: Start with questions you feel most confident about to gain momentum and secure quick points.
Maximizing Efficiency During the Test
As you work through the test, it’s important to remain focused and efficient. Being mindful of your pace can help ensure you leave enough time for more challenging questions while also minimizing the likelihood of rushing through easier ones.
- Work on Time Management Throughout: Periodically check the clock to ensure you’re on track to finish all questions.
- Skip and Return: If a question is taking too long, move on to the next one and return to it later if time permits.
- Don’t Overthink: Trust your initial instincts on questions you’re uncertain about, as second-guessing often leads to errors.
By practicing time management strategies ahead of time, you can reduce stress and approach your test with a clear and confident mindset, leading to a more successful outcome.
Resources for Additional Practice
To enhance your understanding and improve problem-solving skills, it’s essential to regularly practice with a variety of materials. Access to high-quality resources will provide you with ample opportunities to reinforce concepts and master new techniques. There are several excellent options available that cater to different learning styles and offer diverse sets of problems.
Online Platforms
Many online platforms provide interactive exercises and video tutorials that can help clarify difficult topics. These resources are often updated to reflect the latest curriculum changes and exam formats. Below are some popular options:
- Khan Academy: Offers free lessons, practice problems, and instructional videos on a wide range of mathematical topics.
- AP Classroom: A platform specifically designed for students preparing for advanced placement courses, offering practice exams and performance feedback.
- Brilliant.org: Focuses on problem-solving and offers challenging puzzles and interactive courses in mathematics.
Books and Study Guides
Traditional study materials, such as textbooks and comprehensive guides, remain a valuable tool for deepening your knowledge. Many books offer step-by-step explanations and a wide variety of practice problems. Consider the following resources for targeted practice:
- Princeton Review – AP Prep Books: These books provide practice tests, detailed answer explanations, and effective strategies for test-taking.
- Barron’s AP Series: Known for its extensive problem sets and in-depth coverage of key topics, these books are a great way to gauge your readiness.
- Fiveable: Offers study guides and virtual study sessions that cover key concepts and strategies for tackling difficult questions.
By leveraging a combination of online tools and traditional study materials, you can ensure consistent practice and refine your skills in preparation for the test.
Importance of Reviewing Solutions
Reviewing solutions after completing practice problems or assessments is a crucial step in the learning process. Simply solving the problems is not enough to ensure mastery; understanding the steps taken and the reasoning behind each choice is key to improving performance. By analyzing solutions, students can identify mistakes, clarify concepts, and refine their problem-solving strategies.
Why Reviewing Matters
When you review solutions, you not only confirm whether your answer was correct, but also gain insights into how problems can be approached more effectively. This process allows you to:
- Recognize common errors and avoid them in the future.
- Understand alternative methods for solving problems.
- Strengthen your conceptual understanding of complex topics.
How to Review Effectively
To make the most out of your review sessions, it’s essential to approach solutions with a critical mindset. Here are some best practices:
- Work through each step: Don’t just look at the final solution. Go through each part of the solution to understand the reasoning behind every step.
- Identify your mistakes: If you made an error, analyze why it happened. Was it a misinterpretation of the problem, a calculation mistake, or a misunderstanding of the concept?
- Test alternative methods: If there’s more than one way to solve a problem, try each approach to see which one works best for you.
Solution Review Table
| Step | What to Focus On | Action |
|---|---|---|
| Step 1 | Understand the problem | Identify what the question is asking and highlight key information. |
| Step 2 | Work through the process | Carefully follow the method used in the solution, ensuring each operation is correct. |
| Step 3 | Check for errors | Review your calculations and logic to identify any mistakes made along the way. |
| Step 4 | Test alternative methods | Explore different ways to solve the problem to deepen understanding and increase efficiency. |
Incorporating solution reviews into your study routine helps build long-term retention and improves your ability to tackle similar problems in the future. By focusing on the process rather than just the outcome, you enhance your problem-solving skills and increase your overall confidence.
How to Improve Your Calculus Skills
Enhancing your mathematical abilities, particularly in advanced topics, requires consistent practice, a deep understanding of fundamental concepts, and the application of effective strategies. To excel in this subject, you must not only focus on solving problems but also aim to comprehend the underlying principles and how they connect to one another. Building a solid foundation and practicing regularly are key steps to mastery.
Strengthen Your Conceptual Understanding
Rather than memorizing formulas or procedures, focus on grasping the concepts that form the basis of the subject. This will allow you to apply your knowledge in various situations and solve more complex problems effectively. Key strategies include:
- Review foundational concepts: Ensure a strong grasp of basic concepts like limits, derivatives, and integrals, as they are critical for tackling more advanced problems.
- Relate theory to practice: Understand how theoretical principles apply in real-world situations, such as physics or engineering problems, to make the material more relevant.
- Ask questions: Don’t hesitate to clarify doubts with your teacher or peers, and seek explanations for concepts that seem unclear.
Effective Practice Techniques
Practice is essential for reinforcing your knowledge and improving problem-solving skills. However, it’s not just about doing more problems–it’s about doing them correctly and efficiently. Here are some techniques to maximize your practice sessions:
- Work through varied problems: Tackle problems of different difficulty levels and from different topics to ensure comprehensive learning.
- Simulate test conditions: Time yourself while solving problems to improve speed and accuracy under pressure.
- Review solutions thoroughly: After solving a problem, examine the solution carefully to understand each step and to identify areas for improvement.
Improving your skills in this field is a gradual process that demands patience and persistence. By consistently practicing, reviewing solutions, and strengthening your understanding of the subject, you will see significant progress and build the confidence necessary for success.
Using Past Exams for Better Results
One of the most effective ways to prepare for any high-level assessment is to utilize previous years’ tests. These materials not only help familiarize you with the format and style of the questions, but they also provide insight into recurring themes and concepts. By reviewing past assessments, you can identify areas where you need more practice and focus your efforts on mastering these topics. This strategy allows you to approach the material with confidence and optimize your preparation process.
Working through old tests helps you build familiarity with the structure and pacing of the assessment, making it easier to manage time on test day. It also provides an opportunity to understand the types of questions that often appear, allowing you to develop targeted strategies for answering them efficiently.
Furthermore, analyzing the solutions after completing a past test enables you to identify mistakes, learn from them, and avoid making the same errors in the future. This reflective process strengthens your problem-solving skills and ensures that you’re thoroughly prepared for similar challenges in future assessments.