Precalculus Midterm Exam Answers and Solutions Guide

As you approach the upcoming assessments, understanding the fundamental principles that will be tested is crucial. This guide provides you with valuable insights into the essential topics and strategies to ensure you are fully prepared. By focusing on key problem-solving methods and concepts, you can boost your confidence and perform at your best.

Preparation involves not just reviewing formulas and equations, but also developing a clear approach to tackling challenging questions. With the right techniques, even the most complex problems can be simplified and solved efficiently.

Throughout this article, you will find expert advice on how to navigate through each section of your coursework. We will cover various problem types, common pitfalls to avoid, and time-saving strategies that will help you excel in your assessments.

Precalculus Midterm Exam Answers

Mastering complex mathematical concepts requires more than just rote memorization; it involves understanding the underlying principles and knowing how to apply them in different situations. This section will guide you through key problem-solving techniques and help you effectively tackle the most common question types you will encounter.

By breaking down the essential topics and offering clear solutions, this guide ensures that you approach each problem with confidence and precision. Below, you will find a selection of typical questions with step-by-step explanations to solidify your understanding.

Problem Type	Description	Solution Overview
Equations	Solving linear and quadratic equations	Use factoring, completing the square, or the quadratic formula
Graphing	Plotting functions and identifying key features	Analyze intercepts, slopes, and asymptotes
Trigonometry	Solving trigonometric expressions and identities	Apply unit circle and Pythagorean identities
Rational Functions	Working with rational expressions and asymptotes	Find the domain and simplify expressions
Polynomials	Factoring and solving polynomial equations	Use synthetic division or long division methods

By studying these types of problems and understanding the methods behind them, you will be able to approach any question with clarity and efficiency, ensuring a solid performance in your assessment.

Key Concepts to Master for the Exam

To succeed in your upcoming assessment, it’s essential to master the fundamental principles that will be tested. Understanding these core ideas and their applications will help you solve a wide range of problems with ease. Focusing on the key areas that are often emphasized will ensure that you’re fully prepared for any challenges that arise.

Functions are central to many of the problems you will encounter. Familiarize yourself with different types of functions, their graphs, and how to manipulate them. Whether you’re working with linear, quadratic, or exponential functions, knowing how to solve for unknowns and interpret graphical representations is crucial.

Trigonometry is another vital concept to grasp. Understanding the unit circle, trigonometric identities, and the relationships between angles and side lengths will significantly improve your problem-solving skills. Be sure to practice simplifying expressions and solving equations involving sine, cosine, and tangent.

Another important area is polynomials, where you’ll need to know how to factor and solve polynomial equations. This includes using methods like synthetic division, long division, and the Rational Root Theorem. Understanding these techniques will allow you to work through complex expressions with greater confidence.

Finally, it’s essential to be comfortable with rational expressions and complex numbers. Knowing how to simplify and solve problems involving fractions, radicals, and imaginary numbers will give you an edge in tackling more advanced problems.

Understanding Common Precalculus Topics

To perform well in your assessment, it’s crucial to familiarize yourself with the most common mathematical concepts that will be tested. These topics often appear throughout various problems, so understanding their foundations and how they interconnect will give you a significant advantage. Below are several essential areas to focus on to ensure you’re well-prepared for any challenge.

Functions and Their Properties

Functions form the backbone of many problems. Understanding how they behave, how to manipulate them, and how to graph them will allow you to approach a variety of questions with confidence. You should be comfortable with both basic and advanced function types, as well as transformations and compositions.

Trigonometric and Exponential Functions

Trigonometry and exponential functions are among the most challenging yet essential areas to master. You should understand how these functions are used to model real-world phenomena, how to apply identities, and how to solve equations involving these functions.

Topic	Key Concepts	Common Challenges
Functions	Linear, quadratic, polynomial, rational	Graphing and solving equations
Trigonometry	Unit circle, sine, cosine, tangent	Using identities and solving trig equations
Exponential Functions	Growth and decay, logarithms	Solving for unknown exponents

Mastering these key areas will ensure you are prepared for both straightforward and complex problems. Consistent practice and a deep understanding of these topics will be essential for success in your upcoming test.

Solving Equations for Midterm Success

Mastering the process of solving equations is one of the most effective ways to prepare for your upcoming assessments. Being able to quickly and accurately solve different types of equations will help you tackle a wide variety of problems with ease. This section covers essential techniques for solving equations, ensuring that you approach each problem with confidence.

There are several methods for solving equations that you should become familiar with. The most common approaches include:

Isolating the variable: Rearranging the equation so that the unknown is on one side.
Factoring: Breaking down a complex equation into simpler terms that are easier to solve.
Using the quadratic formula: A powerful tool for solving quadratic equations when factoring is not feasible.
Substitution: Useful for systems of equations where one equation is substituted into the other to find the solution.
Graphing: Visualizing the equation on a graph to find the point(s) of intersection.

When solving equations, it’s important to:

Always check your solutions by substituting them back into the original equation.
Pay attention to special cases, such as extraneous solutions that might arise from rational equations or square roots.
Understand how to deal with multiple solutions, especially when working with quadratic or absolute value equations.

By regularly practicing these techniques, you will become adept at solving equations efficiently and accurately, helping you achieve success when it matters most.

How to Tackle Word Problems Effectively

Word problems often seem intimidating at first, but with the right approach, they can be broken down into manageable steps. The key to solving these types of problems is understanding the context, identifying the important information, and applying the correct mathematical techniques. This section provides strategies for approaching word problems in a systematic way to ensure clarity and accuracy in your solutions.

First, carefully read the problem to understand what is being asked. Highlight or underline important numbers, variables, and conditions. Then, translate the words into mathematical expressions. This might involve recognizing the type of problem, such as finding the area, rate, or distance, and using the appropriate formula.

Next, organize the information you have. Create diagrams or tables if necessary to visualize relationships between the variables. This helps in setting up equations or identifying patterns in the problem that might not be immediately obvious.

Finally, solve the equation step by step, checking your work as you go. If your solution doesn’t seem reasonable, revisit the problem to ensure that no key detail was overlooked.

By following these steps, you will develop a methodical approach to solving word problems, increasing both your speed and accuracy. With practice, you will be able to quickly identify the best strategy for each problem, making even the most complex questions easier to handle.

Tips for Graphing Functions Accurately

Graphing functions is an essential skill that allows you to visually interpret mathematical relationships. Understanding how to plot a function correctly can provide valuable insights into its behavior, including key features such as intercepts, slopes, and asymptotes. This section offers practical tips for graphing functions with precision and efficiency.

Identify Key Features Before Graphing

Before you start plotting, it’s crucial to identify the key features of the function. These might include:

Intercepts: Find the x- and y-intercepts by setting the other variable to zero.
Domain and Range: Determine the valid input and output values for the function.
Asymptotes: Identify vertical, horizontal, or oblique asymptotes where the function approaches but never touches.
Symmetry: Check if the function is even, odd, or periodic, which can simplify graphing.

Plot Points and Use a Systematic Approach

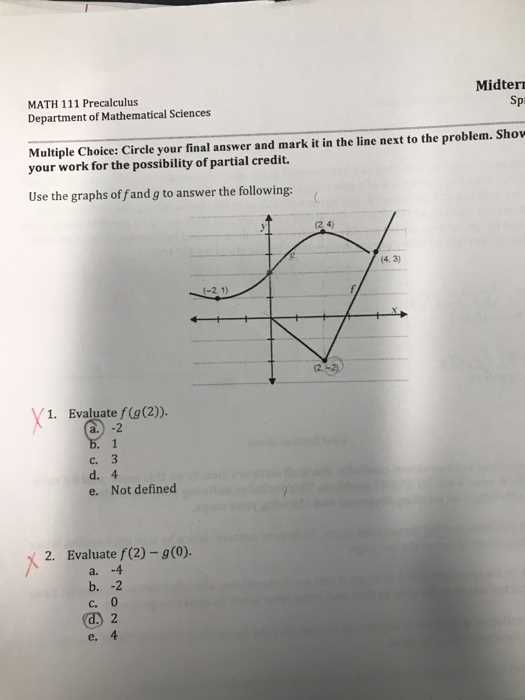
Once you’ve identified the key features, start plotting points on a grid. Begin with critical points such as intercepts and points where the function changes behavior. Use a systematic approach by evaluating the function at various intervals and plotting the results. Connecting these points will help form an accurate representation of the graph.

By following these steps and being thorough in your analysis, you’ll be able to graph any function with confidence and accuracy. Practice regularly to improve your ability to quickly identify key features and plot functions with precision.

Common Mistakes in Mathematical Assessments

Even the most prepared students can make errors during a test, which can lead to incorrect answers and lower scores. Being aware of common mistakes and knowing how to avoid them is crucial for success. This section highlights some of the most frequent errors students make and offers strategies for overcoming them.

Misinterpreting the Problem

One of the most common mistakes is misunderstanding the question or overlooking key details. It’s important to read each problem carefully, noting important terms, variables, and conditions. For example, failing to recognize that a problem asks for the “area” rather than the “perimeter” can lead to entirely wrong calculations. Always double-check the wording and make sure you understand exactly what is being asked.

Forgetting to Simplify or Factor

Another common error is neglecting to simplify expressions or factor equations where necessary. Often, students will solve a problem partially but fail to complete the process by simplifying or factoring the result. This can lead to incorrect or incomplete answers. Make sure to review each step, particularly when working with polynomials or rational expressions, to ensure your final solution is fully simplified.

By being mindful of these common pitfalls and taking the time to check your work, you can avoid many of the mistakes that can cost you valuable points. Regular practice and attention to detail are key to improving your accuracy and performance.

Mastering Trigonometric Identities

Trigonometric identities are powerful tools that simplify complex problems and provide a deeper understanding of mathematical relationships. Mastering these identities allows you to transform expressions, solve equations, and prove other mathematical principles with ease. This section provides essential identities and strategies for working with them effectively.

Start by familiarizing yourself with the fundamental trigonometric identities, which include:

Pythagorean Identities: These relate the basic trigonometric functions, such as sine, cosine, and tangent, in terms of each other.
Reciprocal Identities: These express trigonometric functions as the reciprocals of others (e.g., secant is the reciprocal of cosine).
Quotient Identities: These relate tangent and cotangent to sine and cosine.
Co-function Identities: These show relationships between functions of complementary angles, such as sine and cosine, or tangent and cotangent.
Sum and Difference Identities: These are used to simplify expressions involving the sum or difference of angles.

When working with these identities, follow these steps:

Start by writing down the given expression or equation clearly.
Identify any opportunities to apply fundamental identities, such as converting all terms to sine and cosine.
Simplify the expression step by step, substituting identities where appropriate.
Check your work by verifying that the final result matches the given conditions or equation.

Regular practice with these identities will help you become more efficient and confident in solving trigonometric problems, enabling you to tackle even the most challenging questions with ease.

Preparing for Polynomial Problems

Polynomial problems often appear in assessments and require a solid understanding of how to manipulate and solve expressions involving multiple terms. Being familiar with various techniques for factoring, expanding, and solving polynomial equations will make these problems more manageable. This section focuses on the essential strategies you need to approach polynomial-related questions with confidence.

Start by mastering the basic forms of polynomials and how to identify their degree, leading term, and coefficients. Understanding these features will allow you to recognize different types of problems, such as factoring or solving equations. Practice with different types of polynomials–ranging from simple quadratics to more complex cubic and quartic equations–will give you the skills to handle a wide range of scenarios.

Key methods to prepare for polynomial problems include:

Factoring: Learn techniques like factoring by grouping, using the difference of squares, and applying the quadratic formula.
Long Division and Synthetic Division: These are essential tools for dividing polynomials and simplifying complex expressions.
Rational Root Theorem: Use this to identify potential rational solutions and test them systematically.
Solving Polynomial Equations: Once factored, solving polynomial equations involves finding the roots, often through methods like factoring, graphing, or applying the quadratic formula.

By understanding these techniques and practicing regularly, you’ll be able to approach polynomial problems methodically and accurately, leading to better performance and fewer errors in your assessments.

Strategies for Handling Rational Functions

Rational functions, which involve ratios of polynomials, can be tricky to manage due to their complexity and the potential for undefined values. Understanding how to simplify, analyze, and solve these functions is essential for tackling problems involving them. This section provides strategies for working with rational functions efficiently and accurately.

Simplifying Rational Expressions

One of the first steps when working with rational functions is simplifying the expression. Look for common factors in the numerator and denominator that can be cancelled out. This makes the function easier to work with and reduces the risk of mistakes. Always ensure that any factors canceled are not zero, as division by zero is undefined.

In cases where you can’t immediately factor the expression, consider using polynomial long division or synthetic division to simplify complex rational expressions. These methods help break down the function into a simpler form, making it easier to analyze and solve.

Finding Domain and Asymptotes

Another important aspect of rational functions is understanding their domain and identifying any asymptotes. The domain is restricted by the values of the variable that make the denominator equal to zero. Always set the denominator equal to zero and solve for the variable to determine where the function is undefined.

In addition, rational functions often have vertical and horizontal asymptotes. Vertical asymptotes occur at the values of x where the denominator is zero, while horizontal asymptotes describe the behavior of the function as x approaches positive or negative infinity. To find horizontal asymptotes, examine the degrees of the polynomials in the numerator and denominator:

If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y = 0.
If the degrees are equal, the horizontal asymptote is at y = the ratio of the leading coefficients.
If the degree of the numerator is greater than the denominator, there is no horizontal asymptote (the function may have an oblique asymptote instead).

By following these strategies, you can approach rational functions systematically, ensuring that you simplify expressions correctly, identify key features, and solve problems with greater ease.

Important Formulas to Remember

Having a strong grasp of key mathematical formulas is essential for solving problems quickly and accurately. These formulas provide the foundation for a wide range of problems, from basic algebra to more complex functions. In this section, we will review some of the most important formulas you should remember to streamline your problem-solving process.

Algebraic and Polynomial Formulas

These formulas are fundamental for manipulating and solving algebraic expressions and polynomial equations:

Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a – Solves quadratic equations of the form ax² + bx + c = 0.
Difference of Squares: a² – b² = (a + b)(a – b) – Used for factoring expressions where you have the difference of two squared terms.
Sum of Cubes: a³ + b³ = (a + b)(a² – ab + b²) – Factorization of a sum of cubes.
Binomial Expansion: (a + b)ⁿ = aⁿ + n*aⁿ⁻¹b + … + bⁿ – Expands binomials raised to a power.

Trigonometric and Exponential Formulas

These formulas are crucial for solving trigonometric and exponential problems:

Pythagorean Identity: sin²(θ) + cos²(θ) = 1 – Relates sine and cosine for any angle.
Sum and Difference of Angles: sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B) – Used for simplifying trigonometric expressions involving angles.
Exponential Growth/Decay: y = y₀e^(kt) – Models growth or decay where y₀ is the initial value, k is the growth/decay rate, and t is time.
Logarithmic Identity: logₐ(xy) = logₐ(x) + logₐ(y) – Used for simplifying logarithmic expressions involving multiplication.

By memorizing and understanding how to apply these formulas, you’ll be better prepared to solve problems quickly and accurately, making your approach to any mathematical challenge more efficient.

How to Use Calculators on Your Test

Using a calculator effectively can save you time and reduce the chance of errors during a mathematical assessment. However, it’s important to know how to use the calculator as a tool, not as a crutch. This section covers strategies for using calculators in a test setting, ensuring that you get the most out of the device without relying on it too heavily.

First, familiarize yourself with the functions and features of the calculator you will be using. Many modern calculators offer advanced functions like graphing, solving equations, and performing statistical analyses. Understanding how to access these functions efficiently will allow you to work more quickly when faced with complex problems.

During the test, make sure to use the calculator for operations that are tedious to do by hand, such as large computations, solving equations, or evaluating complex functions. However, always double-check your inputs before pressing the “enter” button to avoid simple mistakes. Additionally, while calculators can speed up numerical calculations, it’s still important to understand the underlying principles behind the problem you’re solving.

Remember to use the calculator to verify your answers when possible. For example, after solving an equation by hand, you can plug the solution back into the equation using the calculator to check if it satisfies the original problem. This approach ensures greater confidence in your results and can help catch errors before submitting your work.

By mastering the use of your calculator and combining it with a solid understanding of mathematical concepts, you will be able to work more efficiently and accurately during your test.

Reviewing Limits and Continuity Concepts

Understanding the concepts of limits and continuity is crucial for solving many advanced problems in mathematics. These principles provide the foundation for analyzing the behavior of functions, particularly as they approach specific points or infinity. This section will cover the essential ideas behind limits and continuity, helping you grasp their application in problem-solving.

Understanding Limits

Limits describe the value that a function approaches as the input variable gets closer to a specific point. It’s essential to understand that limits can exist even if the function is not explicitly defined at that point. For example, a function might approach a value from the left or right, and understanding how to calculate this limit helps in analyzing function behavior near undefined points.

Key things to keep in mind when working with limits include:

Limits can be finite or infinite, and sometimes they approach a specific value or tend to infinity.
When calculating limits, always check if you can directly substitute the value of the input, or if algebraic manipulation (like factoring or rationalizing) is needed.
For one-sided limits, evaluate the behavior of the function as the input approaches the point from the left or the right.

Exploring Continuity

A function is continuous at a point if it is defined at that point, and the limit of the function as the input approaches that point equals the function’s value at that point. Continuity ensures that there are no jumps, breaks, or holes in the graph of a function.

To check for continuity, follow these steps:

Ensure that the function is defined at the point in question.
Verify that the left-hand limit and the right-hand limit at that point are equal.
Confirm that the limit matches the function’s value at that point.

By mastering these concepts, you can gain a deeper understanding of function behavior and approach problems involving limits and continuity with confidence.

Exam Day Tips for Success

The day of a major assessment can be stressful, but with the right strategies, you can stay calm and perform at your best. Proper preparation, a positive mindset, and effective time management are essential for making the most of your time during the test. In this section, we’ll explore key strategies to help you navigate the test day confidently and increase your chances of success.

Preparation Before the Test

Your preparation doesn’t end the night before the assessment. The hours leading up to it are just as important in setting you up for success. Here are some important tips to follow:

Sleep well the night before: Adequate rest helps you stay focused and alert.
Eat a balanced breakfast: Choose foods that provide energy and nourishment, avoiding anything too heavy or sugary.
Arrive early: Arriving with extra time ensures you can settle in and reduce pre-test anxiety.
Stay confident: Trust in your preparation and stay positive about the work you’ve done.

Effective Strategies During the Test

When it’s time to sit down and start the assessment, how you approach each question matters. Here are some useful strategies to keep in mind:

Read each question carefully: Make sure you understand exactly what’s being asked before beginning your work.
Start with easy questions: Work on the problems you feel most confident about to build momentum.
Don’t get stuck: If you’re unsure about a question, move on to the next one and come back later with fresh eyes.
Watch the clock: Keep track of time to ensure you can complete all sections without rushing at the end.

Essential Tools for Success

Bringing the right materials to your assessment can help streamline the process and reduce unnecessary stress. Here’s a checklist of items you should have:

Item	Purpose
Pencil and Eraser	For making clean, correctable marks and adjustments.
Calculator (if allowed)	To aid in solving complex problems more efficiently.
Watch or Timer	To keep track of time and stay aware of how long you’ve been working.
Formula Sheet (if provided)	Quick reference for any formulas you may need to solve problems.

By following these strategies and maintaining a calm, confident mindset, you will increase your chances of achieving your desired outcome. Preparation, organization, and smart time management are all key to approaching your assessment day with success.

Improving Time Management During the Test

Managing your time effectively during an assessment is crucial for ensuring that you can complete all questions without feeling rushed. Time management allows you to allocate sufficient time to each section, giving you the best chance of success. In this section, we will explore practical strategies that can help you use your time wisely and maintain focus throughout the test.

Prioritizing Tasks

One of the first steps in effective time management is determining which questions to tackle first. Start with the sections that are easiest for you, as this will help you build confidence and momentum. By addressing the simpler questions first, you can save time for the more challenging ones later. Here are some useful tips:

Start with what you know: Quickly scan the questions and begin with those that you are most confident about.
Mark tough questions: If a question looks difficult, mark it and return to it after completing the easier ones.
Don’t dwell too long: If you find yourself stuck on a question, move on and come back later.

Managing Your Time Wisely

To ensure that you’re using your time effectively, it’s important to keep track of how long you spend on each section. Having a plan will help you stay on schedule and avoid rushing through the last parts of the assessment. Here are a few strategies:

Set time limits: Decide how much time to spend on each question or section before starting. Stick to these limits to avoid spending too much time on any one task.
Check your progress: Periodically glance at the clock to make sure you’re staying on track.
Leave room for review: Allocate the final few minutes to review your work, making sure that you haven’t missed anything.

By employing these time management strategies, you can ensure that you’re able to navigate the assessment confidently and complete all tasks without unnecessary stress. Efficient time use is key to maximizing your performance on any test.

Breaking Down Complex Word Problems

Complex word problems can be overwhelming, especially when they seem to include multiple steps or variables. The key to solving them effectively is to break them down into smaller, manageable parts. By approaching word problems methodically, you can identify the important information and apply the right methods to reach a solution. In this section, we’ll explore how to simplify word problems and approach them with confidence.

Identifying Key Information

The first step in solving any word problem is to read it carefully and extract the relevant data. Often, problems contain unnecessary details that can distract you, so focusing on what’s important is crucial. Here’s how you can identify key information:

Highlight key numbers: Look for numerical values that are central to the problem.
Identify variables: Recognize what the unknowns are, and assign variables to them if needed.
Understand relationships: Pay attention to how different quantities in the problem are related.

Breaking Down the Problem into Steps

Once you’ve identified the key information, the next step is to break the problem into smaller steps. This will make it easier to follow a logical path to the solution. Here are some strategies for breaking down complex word problems:

Translate the problem: Convert the written problem into a mathematical expression or equation.
Work step-by-step: Solve the problem incrementally, completing each step before moving on to the next.
Double-check each step: After solving each part, pause and review your work to ensure accuracy.

By systematically breaking down word problems and focusing on one step at a time, you can simplify even the most challenging questions. With practice, this approach will help you tackle complex problems with greater ease and confidence.

How to Check Your Answers Efficiently

Reviewing your work is an essential part of ensuring accuracy, but doing so effectively requires focus and a systematic approach. Rushing through the process can lead to missed mistakes, so it’s important to develop strategies that allow you to check your work efficiently without compromising quality. In this section, we’ll explore methods for reviewing your solutions and confirming their correctness in a time-conscious manner.

Establish a Review Strategy

Before starting the review process, it’s crucial to have a clear plan in place. By following a consistent strategy, you can avoid wasting time and ensure that all aspects of the problem are addressed. Consider these strategies:

Work in reverse: Start from your final solution and work backward to see if it logically leads to the initial conditions or assumptions.
Check calculations: Verify each calculation, especially for arithmetic or algebraic operations, as small errors can have a large impact.
Review assumptions: Ensure that the assumptions you made while solving the problem are valid and consistent with the conditions given.

Common Techniques for Efficient Checking

To speed up your review process without sacrificing accuracy, there are several techniques you can use to check your work more effectively:

Estimate before checking: Quickly estimate what the solution should look like, then check to see if your result is within a reasonable range.
Cross-check with different methods: If possible, use an alternative approach to verify your solution. For example, you can substitute your result back into the original equation to see if it holds true.
Use the process of elimination: For multiple-choice or similar questions, rule out clearly incorrect answers to help focus your attention on the more probable solutions.

By following these strategies and techniques, you can enhance the efficiency and effectiveness of your review process. This will not only help you spot mistakes but also build confidence in the correctness of your solutions.

Additional Resources for Review

When preparing for a challenging test, having access to a variety of resources can make a significant difference. There are numerous tools available that can help you solidify your understanding of key concepts, practice problem-solving, and gain confidence in your skills. In this section, we will explore different types of materials and platforms that can assist you during your study sessions.

Online Learning Platforms

One of the most effective ways to review is through interactive platforms that offer video lessons, practice exercises, and real-time feedback. Here are some popular online resources to consider:

Khan Academy: Offers free instructional videos on a wide range of topics, including algebra, functions, and calculus.
Coursera: Features courses from top universities, providing comprehensive reviews on various mathematical concepts.
edX: Provides online courses with in-depth lessons and interactive practice problems tailored to different learning styles.

Textbooks and Study Guides

Traditional textbooks remain a valuable resource for understanding complex theories and working through practice problems. In addition, study guides designed specifically for review purposes can help you focus on the most relevant topics. Consider these options:

Textbooks: Review sections in textbooks that offer clear explanations, worked-out examples, and practice problems with step-by-step solutions.
Study Guides: Specialized study guides such as “Schaum’s Outlines” and “Barron’s” offer condensed information with additional problems and solutions to reinforce key ideas.

Interactive Problem Solving Tools

For hands-on learners, interactive problem-solving tools and apps can be invaluable for practicing various types of problems. These resources allow you to apply what you’ve learned and get immediate feedback on your work. Here are a few tools that may be helpful:

Wolfram Alpha: A powerful computational tool for solving math problems and verifying your work.
Desmos: An online graphing calculator that helps you visualize equations and functions for better understanding.
Symbolab: A problem solver that shows step-by-step solutions for a wide variety of mathematical problems.

Peer and Tutor Support

Sometimes, the best way to clarify difficult concepts is to discuss them with others. Working with a study group or seeking help from a tutor can provide different perspectives and help reinforce your knowledge. Consider these options:

Study Groups: Collaborating with classmates or friends who are also preparing for the same test can allow you to exchange insights and solve problems together.
Tutors: Seeking help from a tutor, whether in person or online, can provide personalized attention and guidance on areas where you may be struggling.

By utilizing a combination of these resources, you can strengthen your understanding of the material, improve problem-solving skills, and increase your chances of success on test day.