Developing a strong foundation in mathematics is crucial for academic success. This section will guide you through essential concepts that will help you navigate and solve challenging problems effectively. Whether you’re working on equations, geometric principles, or basic arithmetic, understanding the underlying principles is key to improving your skills.
Practice and perseverance play a vital role in mastering new techniques. By focusing on different problem-solving strategies and honing your logical thinking, you will gain confidence in tackling more complex topics. A step-by-step approach is often the most effective way to build a solid understanding.
Throughout this guide, you’ll find tips and techniques to enhance your abilities, along with methods to evaluate your progress. With consistent effort and the right resources, anyone can excel in these areas and achieve greater success in their mathematical journey.
Mastering I Ready Level G Math
Building proficiency in mathematical concepts requires dedication and the right approach. As you progress through various topics, it’s essential to focus on key principles and strengthen problem-solving techniques. Understanding the fundamentals and applying them efficiently will allow you to approach even the most complex challenges with confidence.
Building Strong Foundations
Every concept in this journey is interlinked, and a solid grasp of basic skills is the starting point for more advanced material. Focusing on operations, fractions, and algebraic structures will create a framework for tackling higher-order problems. Practicing regularly and refining strategies as you go ensures steady improvement.
Advanced Problem-Solving Techniques
As you master core concepts, you can begin experimenting with more advanced problem-solving approaches. Breaking down complicated problems into smaller, manageable parts is a key strategy. It’s important to stay organized, approach each problem methodically, and always double-check your work for accuracy.
Key Concepts for Success in Level G
Achieving success in this stage of your academic journey involves mastering several core ideas that form the backbone of more complex problem-solving techniques. Focusing on understanding concepts deeply and practicing regularly will enable you to tackle both simple and intricate challenges with ease. Strengthening your grasp on these essential ideas is the key to progressing efficiently.
Understanding Operations and Structures
At the heart of this stage is developing a strong understanding of basic operations and how they interact within different structures. Whether it’s handling numbers, variables, or geometric figures, recognizing patterns and knowing how to apply them to various situations will greatly enhance your problem-solving abilities. This knowledge is vital for moving forward with more complicated concepts.
Critical Thinking and Logical Reasoning
Building critical thinking skills is crucial. Developing the ability to analyze problems, identify key elements, and apply logical reasoning methods will allow you to break down even the most challenging tasks. These thinking strategies will not only help with immediate assignments but will also prepare you for higher-level topics in the future.
Understanding Mathematical Operations in Level G
Grasping the core operations is essential to mastering complex problem-solving techniques. These fundamental tasks are the building blocks that support everything from basic calculations to intricate equations. Whether dealing with addition, subtraction, multiplication, or division, understanding how these operations work together will enable you to tackle more advanced topics with confidence.
Operations with Fractions and Decimals
Fractions and decimals play a crucial role in many mathematical challenges. Recognizing how to convert between the two, perform arithmetic operations, and simplify expressions will enhance your ability to handle a wide range of problems. Mastering these skills will serve as a foundation for more advanced topics like ratios and percentages.
Algebraic Expressions and Equations
Working with algebraic expressions and equations is another key concept. Understanding how to manipulate variables, solve for unknowns, and apply algebraic rules will strengthen your problem-solving abilities. The ability to simplify and solve equations opens the door to solving complex problems in various areas of study.
Strategies for Solving Complex Problems
Approaching difficult challenges requires a clear strategy and the right mindset. Tackling intricate problems can often seem daunting, but breaking them down into smaller, manageable steps makes the process more achievable. With the right techniques, you can navigate even the most complicated tasks efficiently and confidently.
Breaking Problems into Manageable Steps
The first step in solving complex problems is to deconstruct them. Identify the key components, separate the information into smaller chunks, and tackle each part individually. This approach helps simplify the overall task and makes it easier to handle, allowing you to focus on one thing at a time.
Using Logical Reasoning and Patterns
Another essential strategy is recognizing patterns and applying logical reasoning. Look for similarities between the current problem and past challenges you’ve solved. Identifying recurring structures allows you to use proven techniques, making it easier to predict the solution and reduce errors.
Essential Skills for Level G Math
Achieving success in this stage involves mastering a variety of critical skills. These abilities form the foundation for solving more complex problems and understanding advanced topics. Focusing on key concepts such as numerical operations, logical thinking, and pattern recognition will significantly improve problem-solving capabilities.
Developing Strong Arithmetic Skills
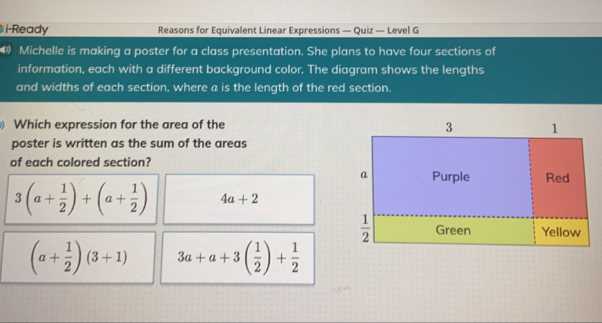
One of the most important skills is a solid grasp of basic arithmetic. Being able to perform operations with speed and accuracy is essential for progressing to more advanced material. Practicing addition, subtraction, multiplication, and division in various contexts will sharpen your ability to solve problems quickly and efficiently.
Enhancing Problem-Solving Techniques
In addition to arithmetic, effective problem-solving techniques are vital. Learning how to approach different types of problems, break them down into manageable steps, and apply logical reasoning will help you navigate challenges with greater ease. Being able to analyze problems from multiple angles is a skill that will serve you throughout your academic journey.
Exploring Word Problems in Level G
Word problems present a unique challenge, requiring not only mathematical knowledge but also strong reading and comprehension skills. To solve these problems effectively, it’s essential to translate the text into mathematical operations and apply appropriate strategies. Understanding the context and identifying key information is crucial to finding the correct solution.
Identifying Key Information in Word Problems
The first step in solving any word problem is to carefully read the problem and extract the most important details. Look for numbers, keywords, and relationships between different elements of the problem. Identifying what is being asked and what information is provided allows you to create a clear plan for solving the problem.
Formulating Equations from Descriptions
Once the essential information has been identified, the next step is to translate the narrative into a mathematical form. This may involve setting up equations or determining the proper operations to use. Understanding how to turn verbal descriptions into mathematical expressions is key to solving these types of problems accurately.
Tips for Efficiently Using the Program
Maximizing the effectiveness of an educational program requires smart strategies and focused effort. By understanding the tools at your disposal and knowing how to use them efficiently, you can improve your productivity and comprehension. The key is to approach each task systematically and make the most of the available resources.
Setting Clear Goals and Priorities
Before starting, establish clear goals for what you want to achieve. Prioritize tasks based on their importance and complexity. By breaking down your objectives into smaller, manageable steps, you will stay focused and ensure that each session is productive.
Tracking Progress and Reviewing Mistakes
One of the most effective ways to ensure continuous improvement is by regularly tracking your progress. After completing exercises, take the time to review mistakes and understand where you went wrong. This reflective approach helps reinforce concepts and prevent similar errors in the future.
How to Tackle Algebraic Expressions
Working with algebraic expressions can initially seem intimidating, but with the right approach, they become much easier to manage. These expressions often contain variables, constants, and mathematical operations that can be simplified or manipulated to solve for unknown values. The key is to break them down step by step and apply the appropriate rules and operations.
Identify Like Terms and Combine Them
The first step in simplifying an algebraic expression is to identify like terms. These are terms that contain the same variable raised to the same power. Once identified, you can combine them by adding or subtracting the coefficients. This reduces the expression to a simpler form.
Apply the Order of Operations
When simplifying an expression with multiple operations, it’s important to follow the order of operations. Start with parentheses, then move to exponents, followed by multiplication and division, and finally addition and subtraction. Keeping this order ensures that the expression is simplified correctly, avoiding errors in the process.
Master Fractions and Decimals in Level G
Understanding fractions and decimals is essential for handling a wide range of mathematical problems. These two concepts are closely related but require different approaches when performing operations. Mastering how to work with fractions and decimals will provide a solid foundation for more complex topics in mathematics and improve overall problem-solving skills.
Converting Between Fractions and Decimals
One of the most important skills is the ability to convert between fractions and decimals. To convert a fraction to a decimal, divide the numerator by the denominator. Conversely, to turn a decimal into a fraction, express the decimal as a fraction of 10, 100, or 1000, depending on the number of decimal places. Being comfortable with both forms allows for greater flexibility in solving problems.
Operations with Fractions and Decimals
Adding, subtracting, multiplying, and dividing fractions and decimals require specific strategies. When working with fractions, it’s essential to find a common denominator before adding or subtracting. For decimals, aligning the decimal points when adding or subtracting ensures accuracy. With multiplication and division, the same basic principles apply, but it’s crucial to understand how to handle the decimal point properly to avoid errors.
Time Management for Level G Math Tasks
Effective time management is crucial for completing mathematical tasks efficiently, especially when faced with complex problems. By organizing your time and prioritizing tasks, you can ensure that you stay focused and meet deadlines without feeling overwhelmed. Developing a strategy for managing time will not only help in completing exercises but also improve your overall learning experience.
Break Tasks into Manageable Segments
One of the best ways to manage time is by breaking tasks into smaller, more manageable segments. Instead of focusing on an entire assignment, divide it into sections that you can complete within a specific time frame. This approach allows you to focus on one part at a time and reduces the risk of feeling overwhelmed.
Set Timed Goals and Track Progress
Setting clear, timed goals for each task is another effective strategy. For example, allocate a certain amount of time to complete a specific exercise or problem. Use a timer or schedule to track your progress and ensure you are staying on track. By setting limits and monitoring your performance, you can prevent procrastination and maintain a steady workflow.
Common Mistakes and How to Avoid Them
When working through mathematical tasks, it’s easy to make simple errors that can lead to incorrect results. Recognizing common mistakes and knowing how to avoid them is essential for improving accuracy and efficiency. Being aware of these pitfalls will help you develop a more disciplined approach to solving problems.
Misinterpreting Word Problems
One of the most common mistakes is misunderstanding the wording of a problem. It’s important to carefully read through all parts of the problem and identify key information. To avoid this mistake:
- Highlight or underline important numbers and keywords.
- Rephrase the problem in your own words to ensure understanding.
- Check for hidden information, such as units of measurement or implied relationships.
Incorrectly Performing Operations
Another frequent error is misapplying mathematical operations, especially in multi-step problems. To reduce the likelihood of mistakes:
- Follow the proper order of operations (PEMDAS/BODMAS).
- Double-check each step before moving on to the next one.
- Use estimation to verify if your final answer seems reasonable.
Building Confidence Through Practice
Developing confidence in solving mathematical problems requires consistent practice and a focused approach. The more you engage with various types of problems, the more comfortable and assured you become in your problem-solving abilities. By repeating exercises and challenging yourself with different levels of difficulty, you can build both your skills and your self-assurance.
Start with Simple Problems
Begin by practicing simpler problems to establish a solid foundation. As you grow more familiar with basic concepts, you’ll gain confidence in tackling more complex tasks. Each small success helps reinforce your ability to approach more difficult problems with a positive mindset.
Challenge Yourself Gradually
Once you’ve mastered basic problems, it’s important to challenge yourself with increasingly difficult exercises. However, it’s essential to progress gradually–don’t jump straight into the hardest problems. By tackling challenges step by step, you reinforce what you’ve learned and feel a sense of accomplishment with each new success.
How to Use Online Resources Effectively
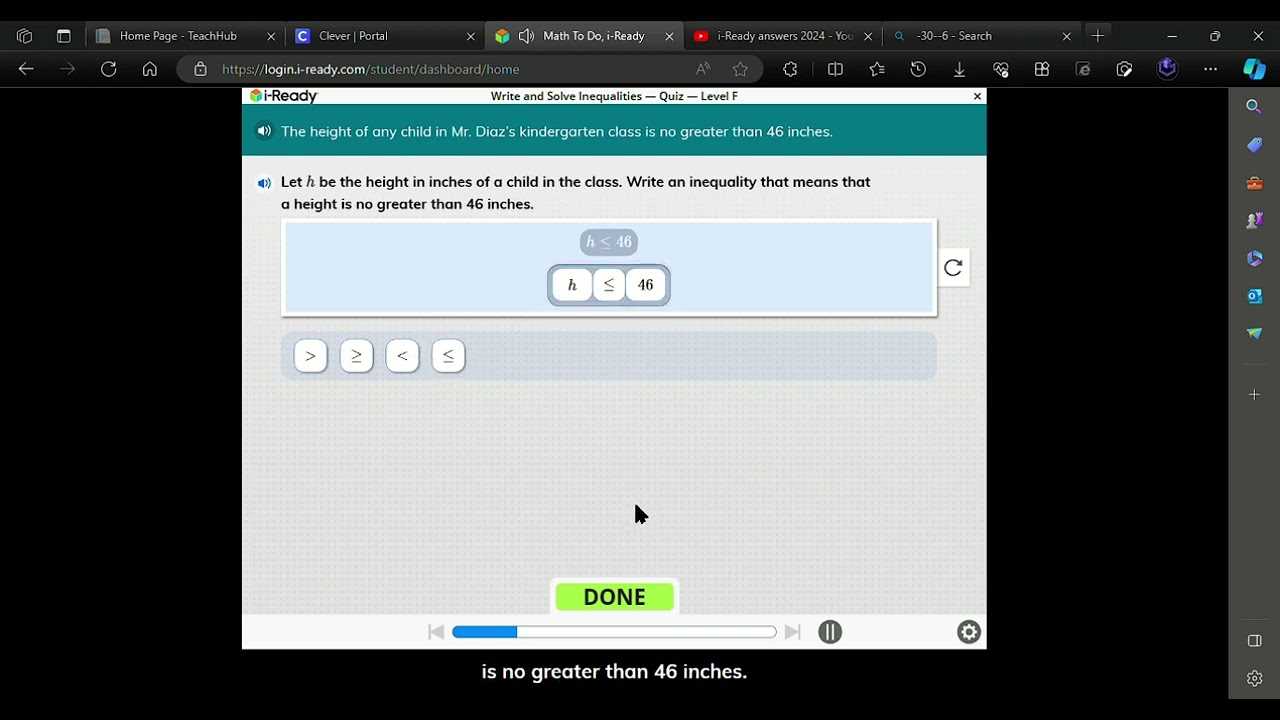
Online resources offer a wealth of tools and information to enhance your learning experience. However, to make the most of these resources, it’s important to use them strategically. Knowing how to navigate these platforms and selecting the right materials can help you grasp complex concepts more easily and improve your skills.
Choose Reputable Websites
Start by identifying reliable and reputable websites that offer quality content. Look for platforms with clear explanations, examples, and interactive exercises. To ensure you are using trustworthy resources:
- Check reviews or recommendations from educational communities.
- Focus on websites with content curated by experts or educators.
- Avoid sources with inconsistent or vague information.
Set Specific Goals
When using online platforms, it’s essential to set clear, achievable goals. Instead of aimlessly browsing, focus on specific topics or skills you want to improve. Here are some tips to stay on track:
- Break your learning sessions into small, focused goals.
- Track your progress regularly to measure improvement.
- Review what you’ve learned before moving on to new material.
Assessing Your Progress in Level G
Tracking your progress is essential to understanding how well you are mastering various concepts. Regular self-assessment helps identify areas where you’re excelling and areas that may require further focus. It provides an opportunity to adjust your learning methods and set new, achievable goals as you continue to improve.
Regular Self-Evaluation
To stay on track, evaluate your understanding periodically. This can be done by revisiting past problems and seeing if you can solve them more quickly and accurately. To assess your progress effectively:
- Review old exercises and compare your previous answers to your current ones.
- Take short quizzes or practice tests to gauge your retention of key concepts.
- Analyze any mistakes and identify patterns that may need more practice.
Set Milestones and Reflect
As you progress, set specific milestones that mark your achievements and reflect on them. This not only helps you measure improvement but also keeps you motivated. Consider these approaches to evaluate your growth:
- Set clear, measurable goals for each study session or week.
- Track improvements in speed, accuracy, and problem-solving strategies.
- Reflect on difficult concepts and assess if you’ve developed a deeper understanding over time.
Improving Test-Taking Skills for Math
Effective test-taking requires more than just knowledge of the subject; it also involves strategies that help manage time, reduce anxiety, and maximize performance. By developing strong test-taking skills, you can approach each exam with greater confidence and efficiency, ultimately improving your results. Understanding how to approach different types of problems and managing your time effectively are key components of success.
Key Strategies for Success
To perform your best during an exam, it is important to implement certain strategies that streamline the process. Here are some tested tips:
| Strategy | Explanation |
|---|---|
| Read Instructions Carefully | Ensure you understand each question before attempting to solve it. Misinterpreting the prompt can lead to unnecessary mistakes. |
| Time Management | Allocate time wisely for each section. Don’t spend too much time on one question; move on and come back later if needed. |
| Eliminate Obvious Mistakes | When reviewing, check for common errors such as calculation mistakes or overlooked instructions. |
Preparing for Success
Preparation plays a critical role in boosting test performance. Regular practice and mock exams help build familiarity and ease with the exam format. Use these preparation techniques:
- Practice with sample problems similar to those you expect to encounter.
- Focus on areas of difficulty and review them thoroughly.
- Simulate real test conditions to improve focus and time management.
Enhancing Logical Thinking for Math
Developing strong logical thinking is essential for solving problems efficiently and effectively. Logical reasoning allows you to break down complex tasks into manageable parts and approach them with a systematic mindset. Whether you are working with numerical puzzles or conceptual challenges, sharpening your logical skills can significantly improve your problem-solving abilities.
Key Components of Logical Thinking
Logical thinking involves several key components that help you analyze problems, make connections, and draw conclusions. Below are some important aspects:
| Component | Explanation |
|---|---|
| Pattern Recognition | Identifying patterns within numbers or shapes helps simplify complex problems and predict outcomes. |
| Deductive Reasoning | Drawing conclusions based on previously known facts or general principles can guide your approach to solving problems. |
| Critical Thinking | Assessing the validity of assumptions, recognizing biases, and evaluating evidence are vital in making sound decisions. |
Building Logical Skills Through Practice
To enhance your logical thinking abilities, consistent practice is key. Try incorporating the following exercises into your study routine:
- Solve puzzles and riddles to boost your ability to identify patterns.
- Engage in activities that require logical deduction, such as strategy games or brainteasers.
- Review mistakes made in previous tasks and identify where your reasoning faltered.
Getting Help When Stuck in Level G
Everyone encounters challenging problems that seem difficult to solve. When you find yourself stuck, it is important to know how to seek help effectively and regain your momentum. Whether it’s clarifying concepts, breaking down complex problems, or finding alternative solutions, there are various strategies to get back on track.
Strategies for Finding Assistance
If you’re having trouble understanding a problem or a concept, consider the following strategies to seek the help you need:
- Ask a Teacher or Tutor: Sometimes a brief explanation can help clear up confusion and offer a fresh perspective.
- Collaborate with Peers: Studying with classmates can help you see problems from different angles, making them easier to solve.
- Use Online Resources: Educational websites and videos often provide step-by-step tutorials that break down difficult topics.
- Review Your Notes: Going over class notes or textbooks can sometimes reveal key information that you missed the first time.
When to Seek Additional Support
It’s crucial to know when to seek help to avoid getting further behind. Here are some signs that it might be time to reach out:
- You’ve spent a considerable amount of time on a problem without making any progress.
- You’re unable to identify where your misunderstanding lies, and it’s preventing you from moving forward.
- You feel overwhelmed or frustrated and need someone to break things down into simpler steps.
Remember, it’s okay to ask for help, and doing so can save time and frustration in the long run. By using these strategies, you can ensure that you keep moving forward and make steady progress.