
When dealing with numbers that are either extremely large or small, traditional methods of representation often fall short. The need for an efficient system arises to handle these values without making calculations cumbersome or complicated. Understanding how to manage such figures can simplify complex mathematical tasks significantly.
By transforming numbers into a more manageable form, it’s possible to simplify arithmetic operations and make patterns more visible. This technique proves especially useful in fields like physics, engineering, and computer science, where precision and ease of calculation are key. Mastery of this method allows for greater flexibility and accuracy in mathematical problem-solving.
Through careful practice, anyone can learn to handle these transformations with ease. Whether it’s for academic purposes or practical applications, this skill is invaluable for anyone looking to enhance their numerical understanding.
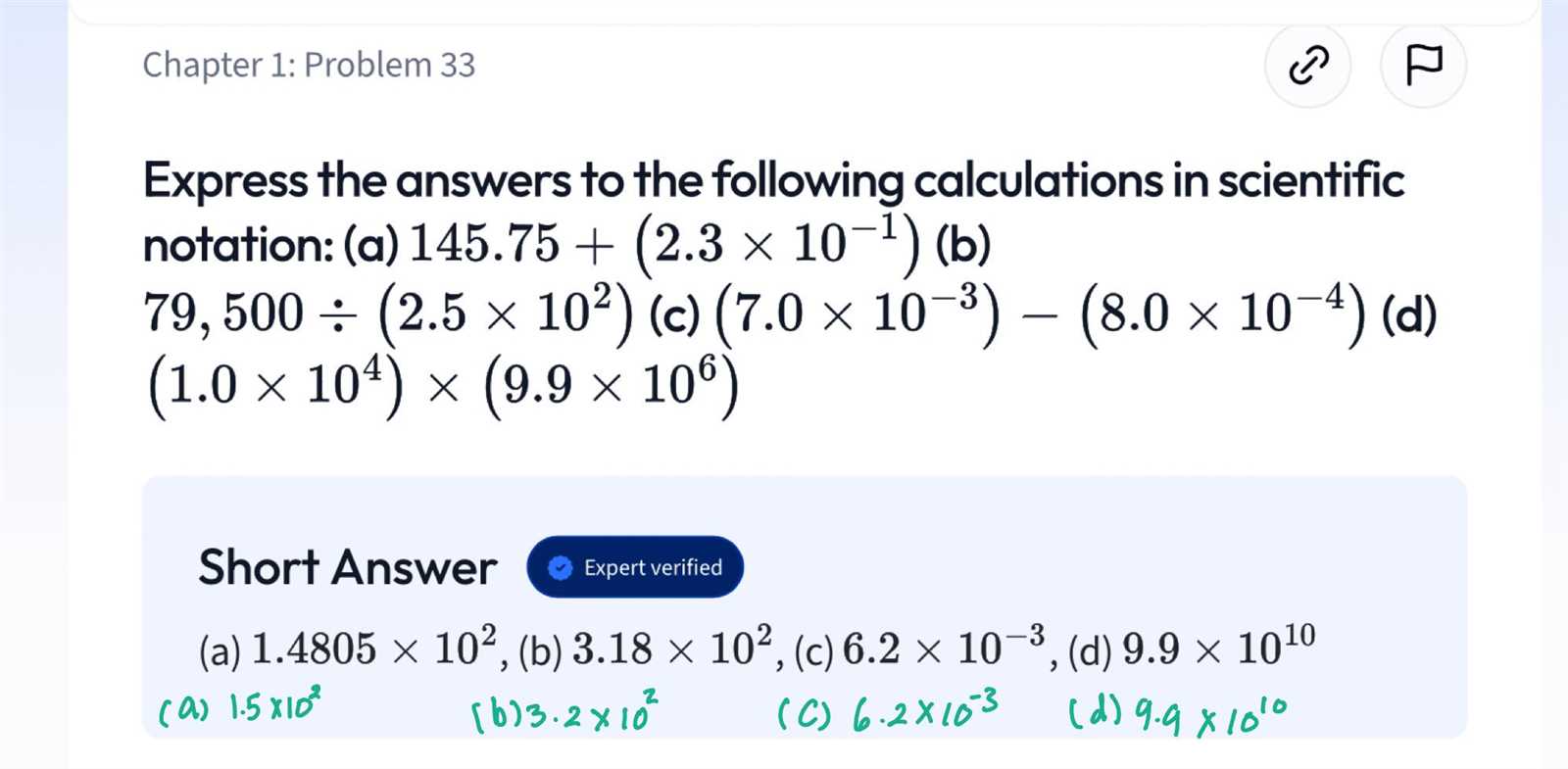
Solve Problems and Express in Scientific Notation
When dealing with numbers that vary greatly in size, finding a clear, efficient way to represent them is essential. This method helps to simplify complex calculations by converting values into a more manageable format, allowing for easier manipulation. Whether you’re working with extremely large or small figures, understanding how to transform these numbers makes arithmetic operations more straightforward.
Understanding the Key Steps
The first step involves identifying the appropriate transformation based on the number’s size. Larger values require a shift to a higher power of ten, while smaller ones are adjusted accordingly. Mastering this process is crucial for anyone looking to tackle calculations that involve a wide range of values, especially in fields like physics, engineering, or data analysis.
Practical Applications in Everyday Math
In everyday use, this skill becomes invaluable when working with measurements, scientific data, or financial figures. It streamlines tasks that would otherwise be complicated by working with unwieldy numbers. By converting them into a more consistent format, it’s possible to perform accurate calculations while minimizing errors and maximizing efficiency.
Understanding Scientific Notation Basics
In many areas of math and science, numbers can grow very large or become exceedingly small. To handle these extremes efficiently, a system is used that makes them more manageable. This method helps represent numbers in a compact form that maintains their value while simplifying calculations.
Key Components of the System
At its core, this system involves two main parts: a base number and an exponent. The base represents the significant digits, while the exponent determines how many times the base should be multiplied or divided by 10. Understanding how these components work together is essential for anyone looking to manipulate large or small values effectively.
- Base Number: The part that contains the significant digits.
- Exponent: Shows how many times the base should be multiplied or divided by 10.
Converting Numbers to a Simplified Form
To convert a number into this format, start by placing the decimal point after the first significant digit. The exponent will then indicate how many places the decimal needs to move. If the number is large, the exponent will be positive, while a small number results in a negative exponent.
- Identify the significant digits in the number.
- Move the decimal point to a position after the first digit.
- Count how many places the decimal was moved; this gives the exponent.
With practice, this method becomes a powerful tool to handle complex calculations and measurements, especially when dealing with vast quantities or extremely small values.
Why Use Scientific Notation in Math
When working with very large or tiny values, traditional methods of representing numbers can become unwieldy. In such cases, a more efficient approach is needed to simplify calculations while maintaining accuracy. By converting these numbers into a compact form, one can easily manage complex mathematical operations and comparisons.
Benefits of Using This System
This approach allows for faster calculations, reduces the risk of errors, and makes it easier to visualize large quantities. It is particularly useful in fields like physics, engineering, and finance, where precision is key, yet the values involved are often far beyond everyday numbers.
| Standard Number | Converted Form | Advantage |
|---|---|---|
| 1,000,000,000 | 1 × 109 | Compact, easy to work with in calculations |
| 0.0000000056 | 5.6 × 10-9 | Simplifies small values for quick comparison |
| 123,000 | 1.23 × 105 | Streamlined for easier mathematical operations |
Practical Applications in Various Fields

In scientific research, for example, this technique makes it possible to represent astronomical distances or subatomic measurements with ease. Similarly, in engineering, it facilitates accurate calculations involving forces, speeds, or electrical currents that span several orders of magnitude.
Converting Large Numbers to Scientific Notation
When dealing with exceptionally large values, it becomes crucial to represent them in a more compact form. By adjusting their scale, these numbers can be expressed in a way that is easier to manipulate and compare. This conversion process helps simplify complex calculations, especially when working with vast quantities or in scientific fields.
To convert a large value, first identify the most significant digits. Then, move the decimal point to just after the first digit. The number of places the decimal moves determines the exponent, which reflects how many times the base value should be multiplied by 10. This step is essential to maintaining the integrity of the number while reducing its complexity.
For example, the number 12,500,000 can be transformed into 1.25 × 107. In this case, the decimal moves 7 places to the left, indicating the exponent. By following this method, any large value can be simplified into a form that is easier to work with in mathematical operations.
How to Convert Small Numbers Easily
When working with very small values, it’s often necessary to simplify them for easier manipulation. Instead of dealing with long decimal places, these figures can be rewritten in a more efficient format that keeps their magnitude intact while reducing their length. This process is essential for accurate calculations, especially in fields that require precision.
Step-by-Step Conversion Process
To convert a small number, start by moving the decimal point to the right until it follows the first non-zero digit. The number of places the decimal moves determines the exponent, which will be negative to reflect the smaller value. This ensures the number stays true to its original size while being much more manageable.
For instance, the number 0.000032 can be rewritten as 3.2 × 10-5. In this case, the decimal moves 5 places to the right, showing the exponent’s negative value. With practice, converting small numbers in this way becomes a quick and reliable method.
When to Apply This Method
This technique is especially useful in scientific measurements, financial calculations, or when working with data that spans multiple orders of magnitude. Converting small values helps avoid errors caused by manually handling many decimal places, ensuring greater accuracy in your work.
Scientific Notation and Exponents Explained
Understanding how large or small values are represented through powers of ten is key to simplifying complex calculations. The process relies on breaking down a number into a base value and an exponent, which indicates how many times the base should be multiplied or divided by ten. This method allows for easy handling of numbers that would otherwise be too unwieldy for practical use.
How Exponents Work

Exponents play a crucial role in this system by showing the magnitude of a number. A positive exponent indicates that the number is large, while a negative exponent is used to represent small values. By shifting the decimal point in the number, the exponent reflects how many places the decimal needs to move.
| Number | Exponent | Converted Form |
|---|---|---|
| 1000 | 3 | 1 × 103 |
| 0.0001 | -4 | 1 × 10-4 |
| 250000 | 5 | 2.5 × 105 |
Using Exponents to Simplify Calculations
By converting values into this form, calculations such as multiplication, division, and comparison become much easier. Working with powers of ten allows for quick adjustments and more straightforward handling of extremely large or small figures, making this method an invaluable tool in many fields such as science, engineering, and economics.
Step-by-Step Guide to Problem Solving
When working with numbers that are either very large or small, a systematic approach is essential for accuracy and efficiency. By following a clear, step-by-step method, the process of handling complex values becomes much simpler. This guide provides a structured way to tackle mathematical tasks that involve shifting values into a more manageable format.
First, start by identifying the key elements of the task. Understand the number’s size and whether it’s large or small. Once you know this, you can determine whether to move the decimal point left or right, which will help you decide on the magnitude of the exponent.
Next, adjust the decimal to position it correctly after the first significant digit. Count how many places the decimal has moved, and this number will form the exponent, reflecting the scale of the value. Ensure you pay attention to whether the exponent should be positive or negative based on the number’s size.
Finally, double-check your work by comparing the result with the original number to ensure the scale and precision have been maintained. With practice, following this step-by-step approach will help make handling large or small numbers a more intuitive process.
Common Mistakes to Avoid in Notation
When converting numbers to a more simplified form, it’s easy to make certain errors that can affect the accuracy and clarity of the result. These mistakes often stem from misunderstanding the rules or skipping steps, leading to confusion or incorrect calculations. Recognizing these common pitfalls is essential for ensuring the process is done correctly every time.
Misplacing the Decimal Point
One of the most frequent mistakes occurs when shifting the decimal point. It’s important to count how many places the decimal moves and apply the correct exponent. Moving the decimal too many or too few places can completely alter the value, leading to incorrect conclusions.
Forgetting to Adjust the Exponent
Another common error is failing to adjust the exponent after moving the decimal. The exponent reflects how many places the decimal has shifted, so neglecting this step means the number won’t be represented correctly. Always ensure that the exponent matches the direction and number of places the decimal has moved.
Understanding the Power of Ten
The concept of powers of ten is fundamental when dealing with large or small numbers. By using ten as the base, it’s possible to express values in a way that makes them more manageable. Powers of ten represent how many times ten should be multiplied by itself to reach a particular value, allowing for a simpler representation of extremely large or small figures.
How Powers of Ten Work
When a number is raised to a power, it tells you how many times to multiply ten by itself. For instance:
- 101 = 10 (10 multiplied by itself once)
- 102 = 100 (10 multiplied by itself twice)
- 103 = 1000 (10 multiplied by itself three times)
Similarly, negative powers represent division by ten. For example:
- 10-1 = 0.1 (1 divided by 10)
- 10-2 = 0.01 (1 divided by 100)
- 10-3 = 0.001 (1 divided by 1000)
Practical Applications
Using powers of ten helps with simplifying calculations and representing numbers more efficiently. Whether it’s working with large distances in astronomy or small measurements in chemistry, understanding how to use powers of ten is essential for accurate data interpretation and problem-solving.
When to Use Scientific Notation
In certain situations, numbers become too large or small to be practical for everyday use. To make such numbers easier to work with, it’s helpful to convert them into a more compact format. This method simplifies complex values, making them more manageable and easier to understand, especially in fields like physics, engineering, or computer science.
Large Numbers
When dealing with very large quantities, such as astronomical distances or the size of a microscopic particle, using a condensed format makes it simpler to express these values without excessive zeros. For example, rather than writing out the number 100,000,000,000, it’s more efficient to represent it as 1 x 1011.
Small Numbers

Similarly, extremely small values, like those encountered in chemistry or biology, benefit from this more efficient format. Numbers like 0.00000000025 can be difficult to read and work with. By converting them to a more concise form, such as 2.5 x 10-10, calculations become much easier to perform.
How to Handle Negative Exponents
Negative exponents may seem tricky at first, but they follow a straightforward rule. They indicate that a number should be divided, rather than multiplied, by the base raised to the positive exponent. Understanding how to work with negative exponents is essential for simplifying expressions and making calculations more efficient.
When you encounter a negative exponent, you can convert it into a fraction. Specifically, a term with a negative exponent in the numerator should be moved to the denominator, and vice versa. For example:
- x-n = 1 / xn
- (1 / x-n) = xn
For instance, 10-3 equals 1 / 103, or 1/1000, which simplifies to 0.001. In this way, negative exponents allow you to represent small values without having to write out many zeros.
Multiplying Numbers in Scientific Notation
When multiplying values in compact form, there are two main steps to follow. First, you multiply the base values together. Then, add the exponents to combine them. This method allows for quick and efficient calculations, particularly when dealing with very large or small numbers.
For example, consider multiplying 3 x 104 by 2 x 106. First, multiply the base values (3 and 2), resulting in 6. Next, add the exponents: 4 + 6 = 10. The result is 6 x 1010.
This approach ensures that multiplication remains simple, even when working with numbers that span several orders of magnitude. The key is to handle the bases separately from the exponents, allowing for a clear and logical process.
Dividing Numbers in Scientific Notation
When dividing numbers written in compact form, the process is quite straightforward. You start by dividing the base values, then subtract the exponents. This method ensures that even very large or small numbers can be divided easily and accurately.
For example, consider dividing 6 x 108 by 3 x 104. Begin by dividing the base values (6 ÷ 3), which gives 2. Next, subtract the exponents: 8 – 4 = 4. The final result is 2 x 104.
By separating the base values and exponents, you maintain a clear path to perform division, allowing for quick simplifications without losing precision. This approach is especially helpful when working with numbers that differ by several orders of magnitude.
Adding and Subtracting in Notation
When performing addition or subtraction with numbers written in compact form, it’s important to ensure that the exponents are the same. This step simplifies the process and makes it easier to combine the base values. If the exponents differ, you’ll first need to adjust the numbers to a common exponent before proceeding with the arithmetic.
Adding Numbers
For example, when adding 4 x 105 and 2 x 105, both numbers already have the same exponent. You can simply add the base values:
- 4 x 105 + 2 x 105 = (4 + 2) x 105 = 6 x 105
Subtracting Numbers
For subtraction, the process is similar. If you have 5 x 106 – 3 x 106, you can subtract the base values directly:
- 5 x 106 – 3 x 106 = (5 – 3) x 106 = 2 x 106
When exponents differ, however, you must first adjust the numbers by converting one so that both exponents are the same. This allows for a straightforward addition or subtraction of the base values.
Real-World Applications of Scientific Notation
Numbers in compact form are often used in fields where large or small quantities are common. From astronomical distances to subatomic particles, this approach allows professionals to express extreme values more easily and manageably. Whether it’s in physics, engineering, or computer science, the ability to handle such values efficiently is crucial for various calculations and analyses.
Astronomy
In astronomy, distances between celestial objects are vast. To simplify expressions, scientists frequently use compact form for astronomical units:
- Distance from Earth to Sun: 1.496 x 108 kilometers.
- Mass of the Sun: 1.989 x 1030 kilograms.
Physics and Chemistry
In physics, the masses of subatomic particles are extremely small, requiring efficient representation. For example:
- Mass of an electron: 9.11 x 10-31 kilograms.
- Charge of an electron: 1.602 x 10-19 coulombs.
Using compact values simplifies communication, reduces errors, and enhances clarity in complex calculations.
Tips for Practicing Scientific Notation
Mastering the use of compact values requires consistent practice and attention to detail. By following a few simple strategies, anyone can become proficient in handling extremely large or small numbers. Whether you are studying for an exam or simply want to improve your skills, these tips can help streamline the learning process and ensure accuracy when using this mathematical approach.
Understand the Basics

Before tackling more complex examples, it’s essential to fully grasp the fundamentals of this method. Familiarize yourself with how numbers are represented in different forms, particularly how exponents reflect the magnitude of the values. Understanding these principles is key to using this system effectively.
- Focus on the power of ten and its role in adjusting the decimal point.
- Practice converting both large and small numbers into this form.
Practice Regularly
Like any mathematical skill, regular practice is essential for improvement. Start with simple exercises and gradually increase the difficulty. Working with a variety of examples will help you become comfortable with manipulating numbers in different contexts.
- Start with basic conversions and build up to more complex operations.
- Try to solve problems involving multiple steps to reinforce your understanding.
Advanced Techniques for Complex Problems
When dealing with intricate tasks that involve large numbers or intricate mathematical manipulations, it is essential to approach them with advanced strategies. These techniques streamline processes, minimize errors, and make it easier to work with very large or very small values. Mastering these methods allows for greater efficiency and accuracy in handling sophisticated calculations.
Breaking Down Exponents
For more complex equations, understanding how to break down exponents can simplify calculations significantly. This technique involves isolating the base number and its corresponding exponent, then handling them separately before combining the results. This method is especially useful when dealing with multiple terms or mixed operations involving powers of ten.
- Distribute powers across terms where necessary.
- Separate components before reassembling to ensure clarity and precision.
Handling Negative Exponents with Precision
Negative exponents can be challenging, but mastering their use is critical when working with extremely small numbers. To manage them effectively, remember that negative exponents represent division by powers of ten. Converting negative exponents into fractions can simplify the process and eliminate errors in complex expressions.
- Convert negative exponents into fractions for easier handling.
- Ensure proper placement of decimal points when working with small numbers.