In many mathematical and scientific problems, one often needs to isolate a specific variable to simplify the problem-solving process. This approach allows for greater clarity and more efficient calculations. By reformatting expressions to highlight one variable, complex problems become easier to understand and solve.
Understanding the principles behind this method is essential. The process involves manipulating equations to place a particular element at the forefront, making it the focal point of the solution. This method is widely applicable in algebra, physics, and engineering, where the need for precise relationships between variables is crucial.
Mastering this skill not only improves mathematical proficiency but also enhances problem-solving strategies in real-world scenarios. By focusing on one key component, it becomes easier to analyze the influence of other variables and make informed decisions based on the simplified expressions.
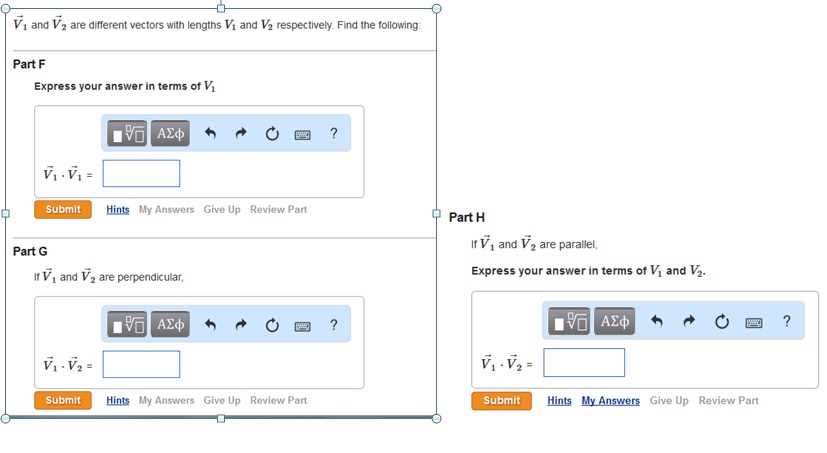
Represent Solutions Using v1
In problem-solving, particularly when dealing with equations or systems of relationships, isolating a specific variable is a powerful technique. This approach simplifies complex expressions and allows for a clearer understanding of how different factors are interrelated. By manipulating equations, it’s possible to highlight a single variable as the key focus, making it easier to solve for or understand the underlying problem.
The goal is to reformulate the equation so that the variable of interest stands out. This process involves rearranging terms and operations to create a more streamlined expression, offering a straightforward path to find the value of the variable. Whether dealing with algebraic equations, physical formulas, or mathematical models, focusing on a single component can provide valuable insights into the system’s behavior.
By focusing on one element, calculations become more manageable, and relationships between different variables become more transparent. This method is especially helpful in fields like physics or engineering, where knowing how a specific factor affects the overall system is essential for making informed decisions.
Understanding the Concept of v1
At the heart of many mathematical problems is the need to simplify relationships between variables. One effective strategy is to isolate a specific variable within an equation or model, making it the focal point for further analysis or computation. This process helps clarify how changes in one factor influence the others, offering a more accessible approach to solving complex problems.
Key Principles of v1 Manipulation
The concept of v1 revolves around identifying the variable that needs to be isolated and then restructuring the equation to highlight it. This often involves performing operations such as addition, subtraction, multiplication, or division on both sides of the equation, ultimately placing v1 in a form that is easy to interpret and solve.
Applications of v1 in Various Fields
Isolating a specific variable is not only useful in mathematics but also in other disciplines like physics, economics, and engineering. In these fields, understanding how individual variables affect systems or models is crucial. By expressing an equation in a way that emphasizes a particular variable, professionals can make more accurate predictions and decisions based on their calculations.
Why Use v1 in Your Solution
Focusing on a specific variable in an equation or model can greatly simplify the process of finding solutions. By isolating v1, you create a clearer path to understanding the relationships between different factors. This approach not only makes calculations more straightforward but also enhances the overall clarity of the problem-solving method.
Utilizing v1 as a central element in your solution allows for greater flexibility when analyzing how changes in other variables affect the outcome. This technique is especially helpful in fields such as physics, engineering, and economics, where precise measurements and predictions are essential. By focusing on one key variable, you can gain deeper insights into how different components interact within a system.
Moreover, working with v1 can help identify potential patterns or trends that may not be immediately apparent in more complex equations. This can lead to more efficient solutions and a better understanding of the problem at hand, ultimately improving decision-making and practical applications.
Key Techniques for Expression in Terms of v1
When solving equations or analyzing relationships between variables, certain strategies are used to isolate and focus on a single element. These techniques help transform complex equations into simpler forms, where the primary variable becomes the focal point. Mastering these methods allows for more efficient problem-solving and clearer insights into the underlying systems.
Rearranging Equations
The most common technique is to rearrange an equation to place v1 on one side while moving all other variables to the opposite side. This often involves using basic operations like addition, subtraction, multiplication, or division. By carefully manipulating both sides of the equation, it’s possible to isolate v1 and express it as a function of the remaining variables. Rearranging helps simplify the problem and makes the solution more accessible.
Substitution Method

Another useful approach is the substitution method, where known values or previously solved variables are substituted into an equation. This allows you to reduce the number of variables in the equation, ultimately isolating v1. By substituting one expression for another, the complexity of the equation is reduced, making it easier to solve for the desired variable.
Mastering these techniques enhances your ability to navigate more complex mathematical models and systems, providing a structured way to focus on a single variable, making calculations more intuitive and manageable.
Common Mistakes When Using v1
While isolating a variable and simplifying an equation can greatly aid in problem-solving, there are several common errors that can occur during this process. These mistakes often arise from misunderstandings of the necessary steps or misapplication of mathematical operations. Identifying and avoiding these errors can help ensure that the solution remains accurate and straightforward.
Incorrect Rearrangement of Equations
One frequent mistake occurs when equations are rearranged incorrectly. This can happen if operations are applied unevenly on both sides, leading to an inaccurate expression. Common errors include:
- Misapplying multiplication or division to one side without doing the same to the other side.
- Forgetting to apply the distributive property when expanding terms.
- Overlooking the order of operations, leading to incorrect results.
Failure to Simplify Properly
Another common issue arises when terms are not simplified adequately after isolating the variable. This can result in a more complicated expression than necessary. Examples of this include:
- Leaving like terms unsimplified, such as not combining constants or coefficients.
- Neglecting to factor out common terms that could make the equation simpler.
- Failing to cancel out common factors when possible, leaving an overly complex expression.
By carefully following the correct procedures and avoiding these common pitfalls, the process of isolating v1 becomes much more manageable and effective.
Step-by-Step Guide to v1 Expression
When isolating a variable in an equation, following a clear sequence of steps ensures that the process is accurate and efficient. By carefully manipulating the equation, each operation builds towards making the desired variable the focus. This step-by-step approach helps to avoid errors and makes the solution process more manageable.
Here’s a simple guide to isolating v1 in a basic equation:
| Step | Action | Explanation |
|---|---|---|
| 1 | Identify the target variable (v1) | Look for the variable that needs to be isolated in the equation. |
| 2 | Move other variables to the opposite side | Use addition or subtraction to shift terms that contain other variables away from v1. |
| 3 | Simplify coefficients | If v1 is multiplied by a coefficient, divide both sides by that coefficient to isolate it. |
| 4 | Check for simplifications | Combine like terms and simplify the equation as much as possible for clarity. |
| 5 | Verify the result | Substitute the isolated v1 back into the original equation to ensure accuracy. |
By following these steps, v1 can be effectively isolated and presented in a form that simplifies further analysis or computation.
Practical Examples of v1 Solutions
Applying the technique of isolating a specific variable is essential in various real-world problems, helping to simplify complex equations and derive meaningful solutions. In different fields such as physics, engineering, and economics, focusing on one key element allows for a better understanding of how different factors influence the system in question. Below are practical examples where this method can be used to solve common problems.
In the following examples, we will walk through the process of isolating v1 to better understand the relationships between variables and how this leads to a more straightforward solution.
Example 1: Physics – Motion Equation
Consider the equation for motion: d = v0 * t + 0.5 * a * t², where:
- d = distance
- v0 = initial velocity
- t = time
- a = acceleration
If we want to find the time (t) in terms of the other variables, we isolate t. Rearranging the equation:
- t = (-v0 ± √(v0² + 2ad)) / a
This gives a solution for t based on the given values of initial velocity, acceleration, and distance traveled.
Example 2: Economics – Profit Equation
In economics, profit (P) is often calculated as P = R – C, where:
- R = revenue
- C = cost
To determine the revenue in terms of profit and cost, we isolate R:
- R = P + C
This simplifies the equation and helps to understand how changes in profit or cost affect overall revenue.
In both examples, the process of isolating a single variable simplifies the analysis, allowing for easier computation and a deeper understanding of the system at hand.
When to Express Answers in Terms of v1
There are specific situations in mathematics and applied sciences when isolating a particular variable is necessary. This approach allows for a clearer understanding of how a single factor influences the overall system, making it easier to solve problems or make predictions. Knowing when to isolate v1 is a critical skill in simplifying complex equations and deriving meaningful insights.
Solving for Unknown Variables
One of the most common scenarios for focusing on v1 is when a problem involves finding an unknown variable. Isolating v1 allows for a solution that can be directly computed once the other variables are known. For instance, in algebraic problems or physics equations, having the desired variable on one side of the equation simplifies the solution process and enables easier calculation of values.
Understanding Relationships Between Variables
Another reason to isolate v1 is to better understand how different variables interact. In many cases, equations represent systems where one factor affects others. By focusing on a single variable, it’s possible to identify the dependency between variables more clearly. This is particularly useful in fields like economics, engineering, and biology, where understanding the influence of one component on another is crucial for making informed decisions or predictions.
In both cases, isolating v1 helps to break down complex problems into more manageable parts, allowing for clearer analysis and faster resolution.
How to Simplify Equations Using v1
Simplifying equations is a crucial skill in algebra and other mathematical disciplines. By focusing on isolating a specific variable, such as v1, it becomes easier to reduce complex expressions to simpler forms. This process not only makes the equation more manageable but also enhances understanding of the relationship between variables. The goal is to make the equation easier to work with, whether solving for a particular value or analyzing the system.
Step-by-Step Process for Simplification
The first step in simplifying an equation with v1 is identifying the variable that needs to be isolated. Once identified, operations such as addition, subtraction, multiplication, or division are applied to both sides of the equation to move other terms away from v1. Afterward, like terms are combined, and coefficients are simplified. This step-by-step process ensures that the equation is as simple as possible while keeping it mathematically correct.
Using Algebraic Properties to Simplify
Algebraic properties such as the distributive property, inverse operations, and factoring are essential tools for simplifying equations. For example, if v1 is part of a more complex expression involving parentheses, applying the distributive property will help break it down. Similarly, using inverse operations helps to cancel out coefficients or terms that might complicate the equation, ultimately leading to a cleaner expression for v1.
By following these strategies, equations can be simplified effectively, making them easier to solve or interpret in practical applications.
The Role of v1 in Problem Solving
In many problem-solving scenarios, focusing on a specific variable, such as v1, can significantly simplify the process. By isolating this variable, the problem becomes more structured, allowing for a clearer path to the solution. This method is particularly helpful when dealing with complex equations where multiple variables are involved. Understanding the role of v1 helps in breaking down a problem into more manageable parts, making the solution process more efficient and straightforward.
Clarifying Relationships Between Variables
In mathematical models and real-world problems, the relationship between variables often plays a key role in determining outcomes. By focusing on v1, the dependency between different factors can be more easily identified. This approach provides a clearer view of how changes in one variable affect the others, ultimately guiding the problem solver toward an accurate and logical solution.
Improving Problem Solving Efficiency
Isolating v1 streamlines the problem-solving process by reducing the complexity of the equation. With fewer variables to manage, calculations become less cumbersome and errors are minimized. This method not only improves efficiency but also enhances the problem solver’s confidence in their ability to tackle similar challenges in the future.
In conclusion, v1 plays a crucial role in simplifying complex problems and improving the overall problem-solving process. By isolating and understanding this variable, solutions can be reached more effectively and with greater clarity.
Benefits of Using v1 in Calculations
Isolating a specific variable such as v1 during calculations offers several advantages, especially when dealing with complex equations. By focusing on a single element, the problem becomes more manageable and easier to solve. This method not only simplifies the calculation process but also leads to more accurate results, reducing the chance of errors and misunderstandings.
One of the primary benefits is the clarity it provides in understanding the relationship between different variables. When v1 is isolated, it’s much easier to observe how changes in other factors influence the desired outcome. This approach also helps in identifying patterns and connections between variables that might otherwise be overlooked in a more complicated equation.
Key Advantages of Isolating v1
The following table summarizes some of the key benefits of using v1 in calculations:
| Benefit | Description |
|---|---|
| Simplification | Breaking down complex equations into simpler forms, making them easier to solve. |
| Clarity | Understanding the relationships between variables and their impact on the outcome. |
| Accuracy | Minimizing the chances of calculation errors by focusing on a single variable. |
| Efficiency | Reducing time spent solving equations, making the process quicker and more effective. |
| Problem Solving | Enabling easier identification of key elements in the problem and finding quicker solutions. |
By leveraging v1 in calculations, the overall efficiency and accuracy of solving equations are significantly improved. Whether in academic problems, scientific research, or real-world applications, this approach enhances the ability to make informed decisions based on clear and precise results.
Solving Real-World Problems with v1
In many practical situations, focusing on a specific variable, such as v1, helps to simplify complex problems and find effective solutions. Whether in engineering, economics, or everyday life, isolating a variable allows for clearer understanding and better decision-making. By applying this technique, problem solvers can approach challenges with a more structured and logical framework, leading to faster and more accurate results.
Examples of Real-World Applications
Here are a few areas where focusing on v1 proves to be essential:
- Engineering – In designing systems or structures, isolating variables like v1 can help determine critical factors such as material strength, load capacity, or energy efficiency.
- Economics – When analyzing market trends or making investment decisions, focusing on a single factor (e.g., interest rates or inflation) allows for a more accurate forecast and strategy development.
- Healthcare – In medical research, isolating specific variables such as v1 (e.g., dosage or treatment duration) helps determine the most effective solutions for patient care.
- Environmental Science – Understanding how one variable, such as v1, influences environmental factors, can aid in creating more sustainable practices and policies.
Steps for Applying v1 in Problem Solving
To effectively solve real-world problems using v1, follow these steps:
- Identify the Problem – Start by recognizing the key factors and challenges in the scenario.
- Isolate v1 – Focus on a single, influential variable to simplify the equation or system of equations.
- Apply Relevant Data – Use available data and information to solve for v1 and understand its impact.
- Analyze Results – Review the outcome to ensure the solution is valid and applicable to the situation.
- Implement the Solution – Apply the results to real-world scenarios and monitor for further improvements.
By applying these steps, individuals can address real-world challenges with greater precision, using v1 to guide their decisions and streamline the problem-solving process.
Transforming Complex Problems into v1
When faced with complex problems, breaking them down into manageable components often leads to more effective solutions. By focusing on a single critical factor, such as v1, it’s possible to simplify intricate systems and identify key relationships. This approach turns seemingly overwhelming challenges into structured tasks, making it easier to find actionable insights and solve the issue at hand. Isolating a particular variable or element reduces unnecessary complexity and allows for a more systematic approach to problem-solving.
One of the primary advantages of this method is its ability to clarify the problem’s core aspects. Instead of getting lost in a web of interdependent variables, focusing on v1 offers a straightforward path to understanding how specific changes affect the overall outcome. This transformation of complexity into a simplified structure ultimately leads to quicker and more precise solutions.
Tools and Methods for v1 Solutions
To effectively solve problems involving v1, it’s important to utilize a combination of tools and techniques that help isolate and focus on this key variable. Various approaches can be used depending on the complexity of the problem and the available data. From basic mathematical models to advanced computational methods, each tool has its specific use in simplifying and analyzing the situation. Whether you’re working with algebraic equations, simulations, or graphical representations, these resources provide a structured way to approach problem-solving.
Common Tools for v1 Analysis
Below are some of the most widely used tools that aid in isolating and solving for v1:
| Tool | Purpose | Applications |
|---|---|---|
| Algebraic Manipulation | Simplifying equations by isolating v1 | Used in basic and advanced mathematics for solving for unknowns |
| Graphical Methods | Visualizing the relationship between variables | Ideal for interpreting data in a more intuitive form |
| Computer Simulations | Modeling complex systems to observe behavior | Applied in engineering, physics, and economics to simulate real-world scenarios |
| Statistical Analysis Software | Analyzing data sets to identify correlations | Used in research and data science to handle large datasets |
Methods for Solving for v1
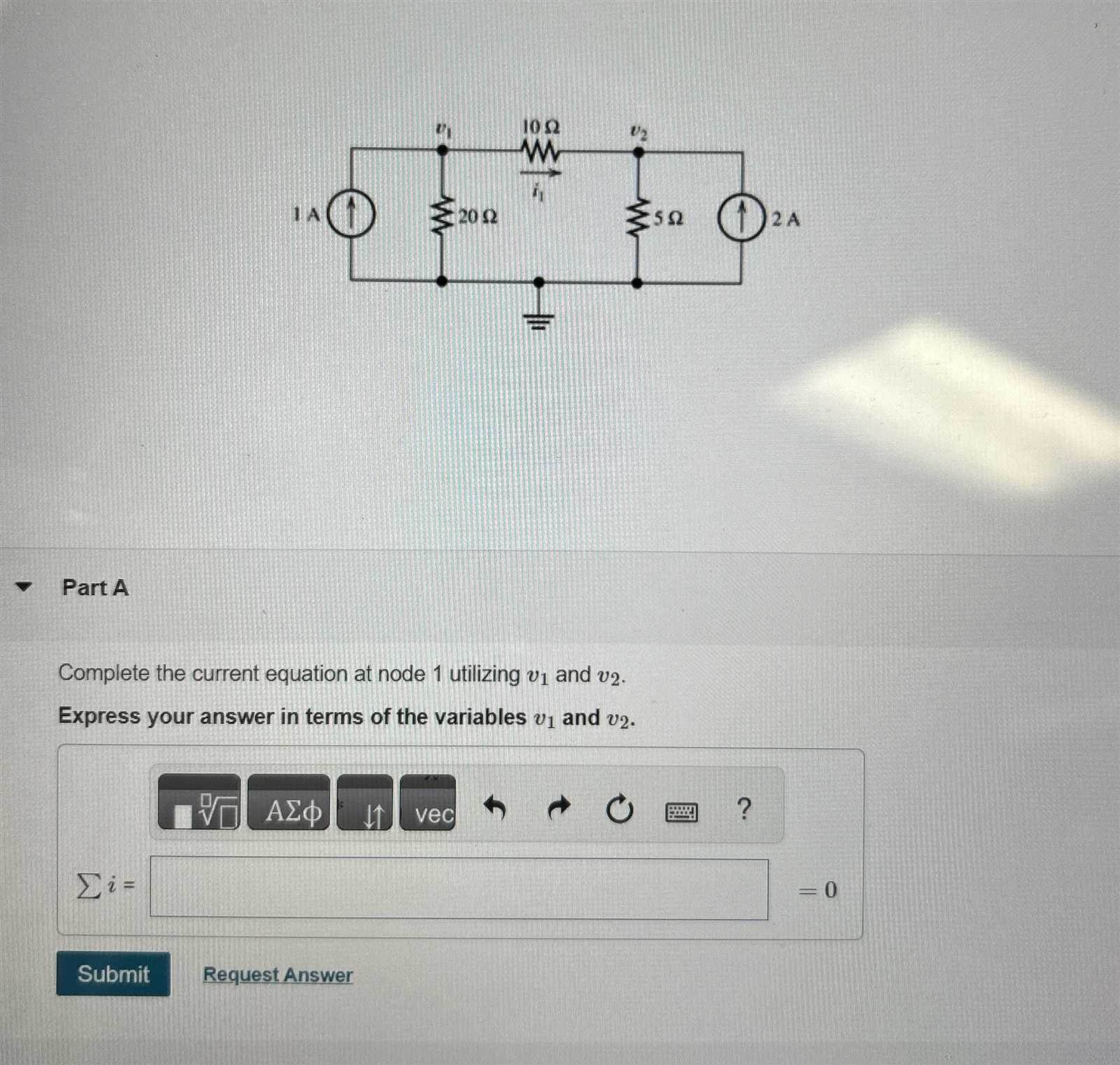
In addition to the tools mentioned above, several methods can be employed to isolate v1 in various types of problems:
- Substitution Method: Substituting known values into equations to find v1.
- Elimination Method: Eliminating other variables from a system of equations to focus on v1.
- Graphing: Plotting the relationships between variables and identifying where v1 can be isolated.
- Numerical Methods: Using computational techniques like Newton’s method to approximate solutions for v1 in complex models.
By combining these tools and methods, you can transform complicated problems into manageable tasks, leading to more efficient solutions for v1 and helping achieve the desired outcomes in various fields.
Advanced Techniques for v1 Manipulation
When dealing with complex problems, especially in higher-level mathematics or applied sciences, advanced methods are often required to manipulate variables like v1. These techniques go beyond basic algebraic operations and incorporate strategies that can handle more intricate equations or systems. Whether you are working with non-linear models, differential equations, or large data sets, these methods provide a structured approach to isolate and manipulate v1 efficiently. Understanding and mastering these techniques allows for more accurate solutions and a deeper understanding of the system at hand.
Key Advanced Methods for v1 Manipulation
Here are some of the most effective strategies used in advanced problem-solving when focusing on v1:
- Matrix Algebra: Solving systems of linear equations involving v1 through matrix operations, especially when dealing with multiple variables and large datasets.
- Differentiation and Integration: Applying calculus to manipulate and solve equations that involve v1, particularly useful in physics and engineering problems.
- Fourier Transforms: Converting complex data sets or signals into simpler forms, making it easier to isolate v1 in wave-related problems or signal processing.
- Optimization Algorithms: Using methods like linear programming, gradient descent, or other optimization techniques to find the best solution where v1 is the key variable.
- Numerical Methods: Employing algorithms like Newton’s method or finite difference methods to approximate solutions for v1 in complex, non-analytic problems.
Practical Applications of Advanced Techniques
These advanced techniques are crucial in fields where precision and efficiency are paramount. Some of the common scenarios where they are applied include:
- Engineering: Designing systems where variables, such as forces or voltages, need to be precisely controlled or calculated.
- Physics: Solving for variables in differential equations that describe physical phenomena such as motion, energy, and thermodynamics.
- Finance: Using optimization methods to solve for rates of return or investment strategies that maximize value.
- Computer Science: Algorithmic problem-solving where v1 represents a critical parameter in computational models, simulations, or data analysis.
By incorporating these advanced methods, you can tackle more sophisticated problems involving v1, yielding more efficient and accurate results across various disciplines.
Common Applications of v1 in Science
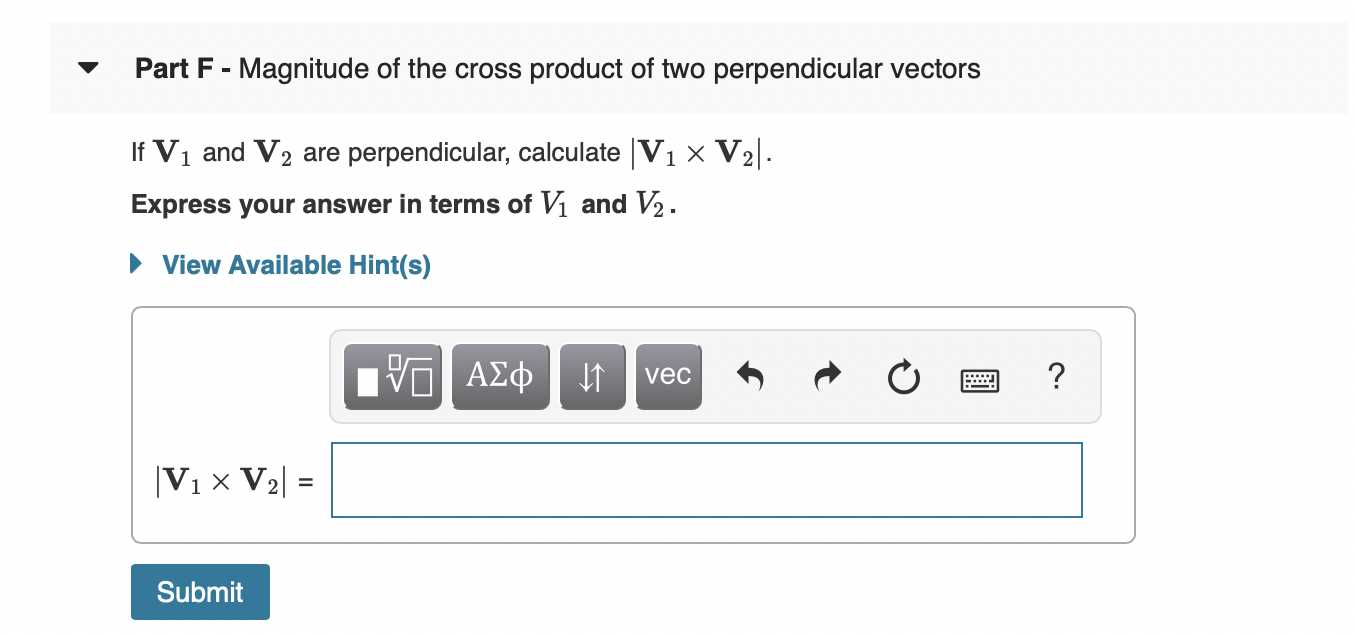
The use of v1 is widespread across various scientific fields, offering a structured approach to solving problems and understanding phenomena. Whether in physics, chemistry, biology, or environmental science, v1 serves as a crucial variable for formulating models, deriving equations, and analyzing data. In each discipline, manipulating v1 allows scientists to isolate and explore key relationships, helping to simplify complex systems or to predict outcomes under different conditions.
Key Scientific Disciplines Using v1
Below are some of the primary areas where v1 plays a significant role:
- Physics: In physics, v1 is often used to represent fundamental quantities like velocity, force, or energy. For instance, in kinematics, v1 may refer to initial velocity, which is essential in calculating the motion of objects under various forces.
- Chemistry: v1 can represent concentrations, reaction rates, or temperature in chemical reactions. By manipulating v1, chemists can predict how changes in one factor will influence the overall reaction.
- Biology: In biological sciences, v1 is frequently used to model population growth rates, enzyme kinetics, or the spread of diseases, helping to predict how systems evolve over time.
- Environmental Science: v1 is often used in environmental modeling, such as calculating pollutant dispersion or determining the rate of resource depletion. By understanding how v1 interacts with other factors, scientists can create more accurate predictions for environmental changes.
Practical Examples of v1 in Scientific Research
In addition to theoretical applications, v1 is crucial in practical research scenarios:
- Modeling the behavior of gases: In chemistry, the ideal gas law uses v1 as a variable to describe the behavior of gases under changing temperature and pressure conditions.
- Population dynamics: In biology, v1 may represent an initial population size, and models use it to predict how populations grow or shrink over time, depending on environmental variables and resource availability.
- Energy transfer: In physics, v1 is often used to denote initial energy levels in systems such as mechanical systems, where energy is transferred or transformed between different states.
- Climate modeling: In environmental science, v1 might represent initial climate conditions, which are used to forecast future changes in temperature, precipitation, or other factors impacting ecosystems.
Across these diverse fields, the manipulation of v1 helps scientists to develop clearer, more predictive models, providing valuable insights and guiding decisions based on reliable data.