Density Review Worksheet Answer Key for Students

Mastering the principles behind physical properties like mass and volume is essential for accurate problem-solving in science. Grasping the relationships between these concepts allows for a deeper understanding of how substances interact and behave under different conditions. Whether in the classroom or in practical applications, applying these ideas correctly ensures precise results in various fields of study.

Effective practice in solving related exercises helps reinforce these foundational skills. By working through exercises that involve calculations and real-world examples, learners can refine their techniques and improve their ability to apply theoretical knowledge. Correct solutions provide valuable insights into the methods required for accurate problem-solving.

For anyone seeking to strengthen their understanding, reviewing worked examples and checking solutions can offer clarity on common mistakes and misconceptions. This process is a key part of mastering the material, enabling learners to become more confident and skilled in their scientific approach.

Density Review Worksheet Answer Key

In order to fully grasp the concepts associated with mass and volume, it is important to have a clear reference for verifying calculations and understanding the correct methods. The following section provides a guide to ensure that each step of the problem-solving process is properly followed. By checking through accurate results, learners can confirm their comprehension and strengthen their approach to practical exercises.

The table below outlines the correct solutions for various problems related to the relationship between mass and volume. Each solution reflects the proper application of formulas, ensuring that the most efficient method is used for accurate results.

Problem	Correct Calculation	Result
Mass of object A (given volume = 5 cm³, density = 2 g/cm³)	5 cm³ × 2 g/cm³	10 g
Volume of object B (given mass = 20 g, density = 4 g/cm³)	20 g ÷ 4 g/cm³	5 cm³
Calculate mass of object C (given volume = 10 cm³, density = 1.5 g/cm³)	10 cm³ × 1.5 g/cm³	15 g
Find volume of object D (given mass = 30 g, density = 3 g/cm³)	30 g ÷ 3 g/cm³	10 cm³

By comparing your own results to the table above, you can identify any areas where further clarification or practice may be needed. Consistently reviewing these solutions helps reinforce a solid understanding of the relationship between mass, volume, and the methods used to solve related problems.

Understanding Density Concepts

Grasping the underlying principles of how substances relate to each other through their physical properties is crucial in many scientific fields. The connection between an object’s mass and its volume plays a fundamental role in determining its behavior in different environments. To build a strong foundation, it’s important to break down the core concepts involved in these calculations and understand the key factors that influence them.

Here are the main concepts that are essential to understanding this relationship:

Mass: The amount of matter in an object, typically measured in grams or kilograms.
Volume: The amount of space an object occupies, often measured in cubic centimeters or liters.
Relationship between mass and volume: The balance between these two properties determines how substances behave under different conditions, including buoyancy and flow.
Formula: The core formula used to calculate the physical property is mass divided by volume, though understanding how and when to apply this formula is key.

These principles are used to predict and explain a wide range of physical phenomena. Understanding how different materials interact with each other–whether in laboratory experiments or real-world applications–requires a solid grasp of these core ideas.

To strengthen your knowledge, consider practicing problems that involve different scenarios, adjusting variables like mass and volume, and interpreting the outcomes based on the relationships discussed.

Ultimately, a clear understanding of these concepts leads to better problem-solving skills and a deeper appreciation for the natural world around us.

Importance of Accurate Calculations

Precise measurements of an object’s mass and volume are crucial for drawing correct conclusions in both theoretical and practical scenarios. Accurate results are the foundation of any scientific analysis, ensuring that predictions and experiments are reliable. Whether working in a laboratory or applying concepts to real-world situations, the importance of correctness cannot be overstated. Small errors can lead to significant misunderstandings and affect the outcome of larger projects.

Consequences of Inaccurate Results

Inaccurate calculations can cause numerous issues, especially in fields where precision is essential. Some of the potential consequences include:

Incorrect conclusions: A slight miscalculation can alter the interpretation of an experiment, leading to misleading results.
Flawed designs: Engineers and designers rely on accurate data to develop functional systems or products. Any error could lead to costly mistakes.
Safety risks: In fields like chemistry or material science, improper measurements could result in dangerous reactions or structural failures.
Wasted resources: Incorrect calculations can lead to inefficient use of materials, energy, or time in both experimental and industrial settings.

Ensuring Precision in Measurements

To achieve the most reliable results, it is crucial to follow a systematic approach when performing calculations:

Use accurate instruments: Ensure that measurement tools are calibrated and functioning properly.
Double-check your work: Repeating calculations and verifying units helps catch any potential mistakes.
Understand the method: Having a clear understanding of the process ensures that each step is completed correctly.
Account for variables: Make sure all factors affecting the measurement are considered, including temperature, pressure, and material properties.

By paying attention to detail and applying these practices, it is possible to maintain accuracy and ensure that the results are both meaningful and reliable.

Key Terms in Density Problems

When tackling problems related to mass, volume, and their interrelationship, understanding key terms is essential for effective problem-solving. These terms form the foundation for the calculations and conceptual applications necessary to solve related exercises. Familiarity with these terms ensures clarity in both understanding the problem and applying the correct methodology to find solutions.

Below are the most important terms to grasp when working through these types of problems:

Mass: The amount of matter contained within an object, typically measured in grams (g) or kilograms (kg).
Volume: The amount of space an object occupies, often measured in cubic centimeters (cm³), liters (L), or milliliters (mL).
Unit of Measurement: The standard used to quantify mass and volume. Common units include grams, kilograms, liters, and cubic centimeters.
Formula: A mathematical expression used to calculate the relationship between mass and volume. The most common formula is mass divided by volume to determine an object’s physical property.
Buoyancy: The ability of an object to float or sink in a fluid, influenced by its physical property relative to the fluid.
Substance: The material from which an object is made, which can affect how its mass and volume relate to one another.

By familiarizing yourself with these fundamental terms, you can better approach problems that require calculating or understanding the relationship between mass and space. Clear definitions make it easier to navigate the steps involved in these calculations and ensure greater accuracy in problem-solving.

Step-by-Step Solution Process

Solving problems related to the relationship between mass and volume involves a clear and methodical approach. By following a structured process, you can ensure that each step is performed accurately, leading to correct solutions. Understanding how to break down the problem and apply the appropriate formulas is key to achieving reliable results.

Breaking Down the Problem

The first step is to carefully read the problem to identify the given values and what needs to be calculated. Once you have a clear understanding of the situation, follow these steps:

Identify known values: Determine which quantities are provided in the problem, such as mass, volume, or any other relevant details.
Identify unknown values: Understand what needs to be calculated. Typically, this will be a property like mass or volume.
Choose the correct formula: Select the formula that relates the known and unknown quantities, ensuring it’s the right equation for the problem at hand.
Double-check units: Ensure that all units are consistent before performing calculations. Convert units if necessary to avoid errors.

Executing the Calculation

Once the problem is broken down, it’s time to perform the calculation:

Substitute the values: Plug the known values into the formula carefully, making sure each variable is correctly placed.
Perform the calculation: Carry out the arithmetic operations needed to solve for the unknown quantity.
Check your result: After obtaining a result, review it to ensure it makes sense. Is the value reasonable? Does it match the expected outcome based on the problem description?

By following this clear and systematic approach, you can solve related problems with confidence, ensuring accuracy in every step of the process.

Common Mistakes in Density Worksheets

When working on problems related to mass, volume, and their relationship, students often make a variety of mistakes that can lead to incorrect results. These errors can stem from misunderstanding the concepts, overlooking important details, or misapplying formulas. Identifying and avoiding these common mistakes is crucial for improving accuracy and gaining a better understanding of the material.

Incorrect Unit Conversion

One of the most frequent errors occurs when students fail to convert units correctly. Since mass and volume are often measured in different units, it’s essential to ensure that all units are consistent before performing any calculations. Common mistakes include:

Forgetting to convert units, such as using grams when the problem requires kilograms.
Mixing incompatible units, like cubic centimeters and liters, without converting them properly.
Omitting unit conversions altogether when given a set of measurements in different units.

Misapplication of Formulas

Another common mistake is using the wrong formula or misapplying it. This can happen when students confuse different equations or forget to rearrange the formula correctly. Some frequent errors include:

Using the wrong formula to calculate mass or volume, especially when dealing with related properties.
Forgetting to rearrange the formula before performing the calculation.
Substituting values incorrectly into the equation, leading to invalid results.

Being aware of these common mistakes and practicing careful attention to detail can help avoid errors and lead to more accurate solutions when tackling these types of problems.

How to Solve Density Problems Efficiently

Solving problems related to mass, volume, and their interrelationships can sometimes be complex, but with the right approach, you can work through them quickly and accurately. The key to efficiency is understanding the core principles and applying a step-by-step strategy that minimizes mistakes and maximizes speed. By mastering the process, you can tackle any related problem with confidence and ease.

1. Understand the Problem Clearly

Before diving into calculations, make sure you fully understand the problem at hand. Take a moment to identify the given information and determine what is being asked. Understanding the question is the first step to finding the right solution. To speed up your approach, consider the following:

Identify known and unknown values: What information is provided, and what needs to be calculated?
Focus on units: Ensure that the units of mass and volume are consistent or convert them as needed.
Reword the problem: Restating the problem in simpler terms can often reveal insights and help guide your approach.

2. Use a Structured Approach

Once you have a clear understanding of the problem, apply a methodical approach to solving it. This ensures that you stay on track and avoid errors:

Apply the right formula: Select the appropriate equation based on the information provided.
Perform calculations in order: Start with simple operations and check your work as you go.
Check your results: After solving, always review your calculations to ensure they make sense and are in the correct units.

By following these steps, you can complete calculations quickly while maintaining accuracy, making the process far more efficient.

Practical Applications of Density

The relationship between mass and volume plays a crucial role in a wide variety of real-world applications. By understanding how these properties interact, we can better navigate challenges in fields such as engineering, medicine, and environmental science. From designing buoyant objects to analyzing the properties of different materials, this concept is foundational in solving many practical problems.

In engineering, for example, calculating how compact a material is can influence decisions about which materials to use for different construction projects. Lighter materials may be chosen for products that need to float, while denser materials are selected for projects requiring strength or durability. The ability to determine the compactness of a material helps engineers optimize resources and create more efficient designs.

In medicine, understanding how substances interact with one another based on their mass and volume is vital for creating accurate diagnostic tools. For example, the behavior of fluids in the human body, such as blood, can be studied through these principles to better understand diseases or develop treatments.

Environmental scientists also rely on these principles to monitor pollution levels, assess the movement of pollutants in water bodies, and develop strategies to mitigate environmental damage. By understanding how different substances behave in various conditions, researchers can make more informed decisions to protect ecosystems and human health.

Interpreting Results from Density Calculations

Once calculations involving the relationship between mass and volume are complete, the next crucial step is interpreting the results. These calculations provide important insights that help explain the physical properties of the substance being studied. However, simply obtaining a number is not enough; it’s essential to understand what that number represents in a practical context and how it can be used to draw meaningful conclusions.

Analyzing Numerical Results

When interpreting the outcome of these calculations, the first thing to consider is the magnitude of the result. For example, a higher value might indicate a compact material, while a lower value suggests a more porous or less compact substance. Depending on the situation, the result may be compared to known standards or expected values:

Comparison with known values: If you’re working with a common material, you can compare your calculated result to known reference values to verify the accuracy of your calculation.
Assessing reasonableness: Ensure that the result makes sense in the context of the problem. If the value seems unusually high or low, recheck the units, conversions, and the formula applied.

Practical Implications of Results

After confirming that your results are accurate, consider their practical implications. The calculated value can help determine a material’s suitability for a specific application. For instance, if you’re designing a boat, knowing whether a material will float or sink based on its properties is essential. In other contexts, like manufacturing, the results can influence decisions about material strength and performance under different conditions.

By interpreting these results effectively, you can gain a deeper understanding of how mass and volume relate to the world around you and use that knowledge to make informed decisions in a variety of fields.

Tips for Memorizing Density Formula

Mastering the formula that relates mass, volume, and their relationship is essential for solving a variety of problems in physics and chemistry. While the formula itself is straightforward, remembering it accurately and applying it effectively in different contexts can be challenging. Fortunately, there are several strategies that can make this process easier and help reinforce your understanding.

One effective method is to break down the formula into smaller, more manageable components. Focus on understanding what each variable represents and how they interact. This deeper comprehension can make the formula feel more intuitive, making it easier to recall when needed.

Another helpful technique is to create mnemonic devices or memory aids. For example, using phrases or acronyms that represent the variables in the formula can serve as a quick mental reminder. Visual learners might find it helpful to draw diagrams or charts that demonstrate the relationship between the variables, reinforcing the concept through imagery.

Lastly, consistent practice is key. Regularly working through problems and applying the formula in different scenarios not only strengthens memory but also builds confidence in using it correctly. The more you work with the formula, the more automatic it will become.

Real-World Examples of Density

The concept of mass per unit volume is not just an abstract idea; it has numerous applications in the real world. From everyday objects to complex scientific phenomena, understanding how mass and volume interact is essential in a wide range of fields. These examples highlight how this fundamental concept shapes everything from natural processes to technological innovations.

Buoyancy in Water: One of the most common examples is the principle that governs whether an object will float or sink in water. An object with a lower mass-to-volume ratio than water will float, while one with a higher ratio will sink. This is why ships, despite their massive size, can float on the ocean, while small stones may sink right away.

Airplanes and Aircraft Design: In aviation, engineers must consider the weight and air volume of materials to create efficient and safe flying machines. The materials used in aircraft are specifically chosen for their ability to be both lightweight and durable, which directly ties to the relationship between mass and volume. This knowledge helps manufacturers design planes that are capable of achieving lift and flying at high altitudes.

Oil Spills and Environmental Studies: When dealing with oil spills, understanding the mass-to-volume ratio of various liquids can be critical. Different oils have distinct mass-to-volume ratios, which affect their ability to spread or sink when spilled. This information is used to determine the best methods for cleanup and to predict the environmental impact on water bodies.

Food and Cooking: In the kitchen, mass and volume considerations influence cooking techniques. For example, the density of ingredients like flour and sugar can affect the texture of baked goods. Understanding how these ingredients interact helps chefs create the right consistency in recipes, ensuring the desired outcome for dishes.

Visualizing Density Through Diagrams

One of the most effective ways to understand the relationship between mass and volume is by using visual aids. Diagrams and illustrations can simplify complex concepts and make it easier to grasp how different substances behave under various conditions. By visually representing how particles are arranged and how their interactions affect a material’s properties, learners can gain a clearer understanding of physical concepts.

Using Particle Diagrams

Particle diagrams are a great tool for visualizing how mass and volume influence the behavior of a material. These diagrams typically show particles (atoms or molecules) arranged in a specific pattern, illustrating how closely they are packed. For example, in materials with a higher mass-to-volume ratio, the particles will be closely packed together, creating a denser substance. Conversely, in less dense materials, the particles will be more spread out.

Visualizing with Volume vs. Mass Graphs

Another helpful visualization tool is the graph that plots mass against volume. By understanding how these two quantities interact, learners can easily observe the relationship. A steep slope on such a graph represents a material with a higher mass for a given volume, indicating a denser substance. A flatter slope would suggest a lower mass-to-volume ratio, representing a less dense substance.

Material	Mass (g)	Volume (cm³)	Mass-to-Volume Ratio (g/cm³)
Lead	113.5	10	11.35
Wood	50	50	1
Oil	92	100	0.92

By comparing materials in a table like this, learners can quickly see the difference in mass-to-volume ratios. Visualizing these relationships in both particle diagrams and graphs helps clarify the concept and supports deeper learning.

Using Units Correctly in Density Calculations

Accurate calculations require attention to the units used for both mass and volume. When calculating the ratio between these two quantities, the units must align properly to ensure the result is meaningful. The precision of the outcome relies on correctly converting, canceling, and maintaining consistent units throughout the process. A solid understanding of how to handle these units is essential for producing reliable results.

Choosing the Right Units for Mass and Volume

When performing calculations, it’s important to select appropriate units for both mass and volume based on the context. For example, mass is often measured in grams (g) or kilograms (kg), while volume might be given in cubic centimeters (cm³) or liters (L). To avoid errors, always ensure that the units are compatible with each other and the final desired outcome. In some cases, converting between units may be necessary. For instance, if you are working with kilograms for mass and liters for volume, you might need to convert to grams and cubic centimeters for a consistent ratio.

Unit Conversion and Consistency

Unit conversion is a critical step in ensuring accurate results. If mass is measured in kilograms but volume is given in cubic meters, it’s essential to convert one or both units before performing any calculations. Additionally, it’s important to ensure that both mass and volume are expressed in consistent units before calculating the ratio. For example, if mass is in grams and volume is in milliliters, the result should be expressed in grams per milliliter (g/mL). Always check for unit consistency to avoid confusion and maintain calculation accuracy.

Example of Unit Conversion: If you are working with a material with a mass of 2000 grams and a volume of 2 liters, but you want the final result in grams per cubic centimeter (g/cm³), you would need to convert the volume from liters to cubic centimeters (1 liter = 1000 cm³) before performing the calculation.

Final Tip: Always double-check the units before starting a calculation and after reaching a final result to ensure the correctness and clarity of your answer. This simple step can prevent many common errors and ensure the reliability of your findings.

Understanding Mass and Volume Relationships

The relationship between the amount of matter in an object and the space it occupies is fundamental to understanding how materials behave under different conditions. This connection helps in determining how objects will interact with one another, such as whether they will float or sink when placed in a fluid. Knowing how to relate mass to volume is key to solving many problems in science and engineering.

Mass refers to the quantity of matter present in an object, typically measured in grams or kilograms. Volume, on the other hand, is the amount of three-dimensional space the object occupies, often measured in liters or cubic centimeters. These two quantities are directly related through specific formulas, and understanding how they interact allows for a more complete understanding of physical properties.

The relationship between mass and volume can be described as proportional, meaning that if one of these values increases, the other will change accordingly. For example, when the volume of an object increases, its mass will also increase if the material remains the same. This direct relationship is crucial for predicting how an object will behave in different environments and for making comparisons between different materials.

In many cases, the ratio between mass and volume provides a unique identifier for materials, and this ratio plays a central role in calculating other important properties. For example, objects made of the same material will have the same ratio, regardless of size, which allows scientists to determine the identity of a material or its behavior in various conditions.

Understanding this relationship also helps in practical applications like designing ships, aircraft, and other structures, where knowing how materials will behave under different stresses is essential for safety and efficiency.

Challenges in Solving Density Problems

Solving problems related to the relationship between mass and volume can present several difficulties, even for those with a strong understanding of basic mathematical concepts. The challenges often arise when trying to apply the correct formulas, converting between different units, or interpreting complex situations where multiple variables are at play.

Common Difficulties in Unit Conversion

One of the most frequent obstacles is the proper conversion of units. In these problems, mass and volume are typically measured in different units, such as grams versus kilograms or milliliters versus liters. Ensuring that all measurements are in compatible units is crucial for an accurate result, and even small errors in conversion can lead to significant mistakes in calculations.

Understanding Complex Objects and Materials

Another common challenge is dealing with objects made of multiple materials or those that are irregularly shaped. When an object is composed of several substances, each with different properties, it becomes more difficult to determine the overall relationship between mass and volume. In these cases, knowing how to break down the problem and apply the correct method to each part is essential for accurate results.

Additionally, many problems involve materials with unknown properties or that require approximations. In these situations, assumptions must be made based on prior knowledge or estimates, which can introduce a margin of error. Being able to identify when assumptions are reasonable and when they might cause inaccuracies is an important skill in solving these problems effectively.

Despite these challenges, mastering the techniques for solving mass-to-volume problems can lead to a deeper understanding of how materials interact in the physical world. With practice, students and professionals alike can become more comfortable navigating these difficulties and applying the appropriate solutions.

How to Verify Your Results

After solving problems involving the relationship between mass and volume, it is essential to verify that the results you obtained are accurate. Verification helps to ensure that no errors were made during calculations and that the answer is reasonable within the context of the problem. There are several strategies you can use to check the correctness of your solutions.

Double-Check the Formula Used

The first step in verifying your results is to confirm that you applied the correct formula for the calculation. Ensure that you are using the appropriate equation to solve for the unknown variable. Common formulas include those relating mass, volume, and other properties that are typically involved in such problems.

Unit Consistency

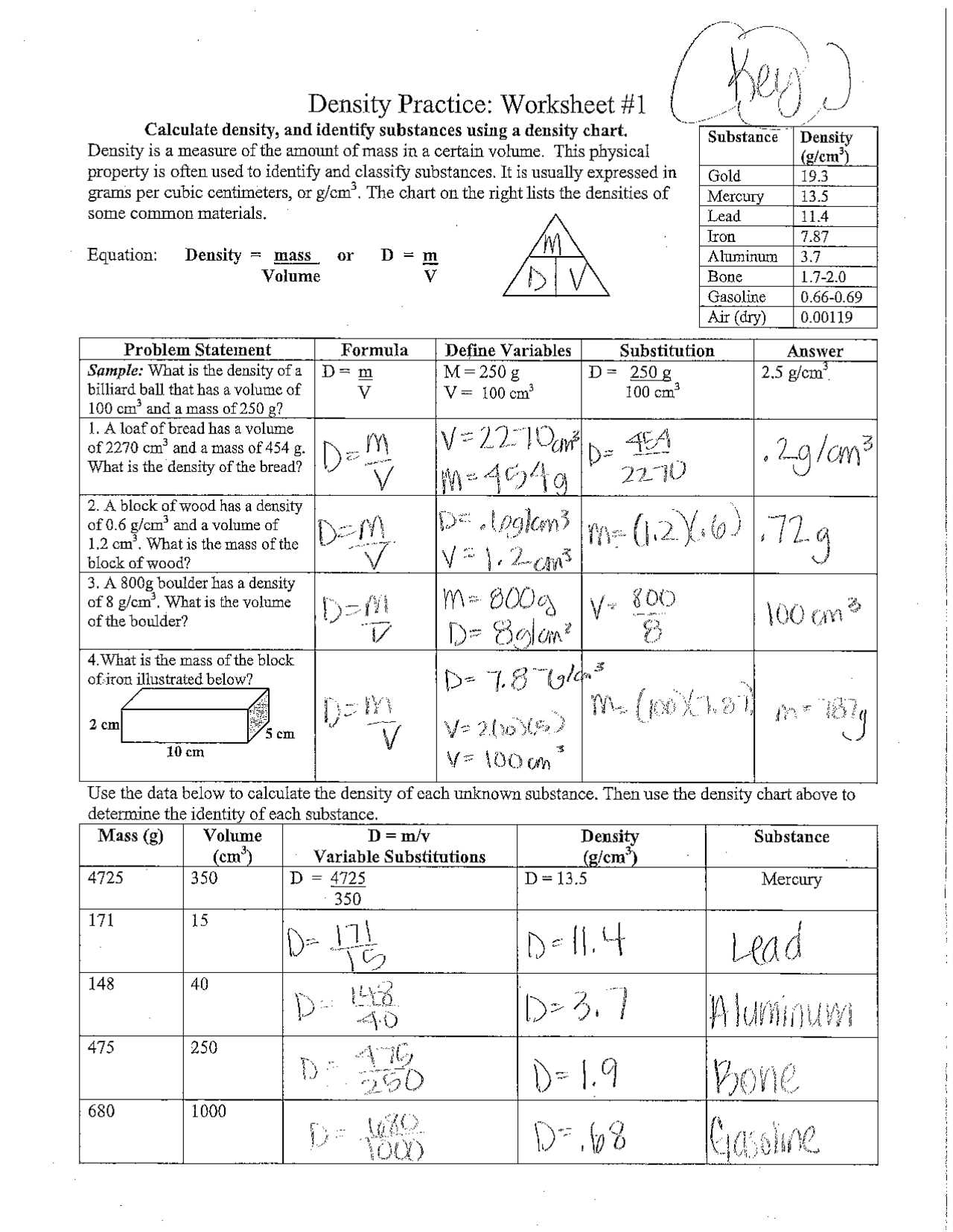
Verify that all units are consistent throughout the calculation process. One of the most common sources of errors is when mass and volume are measured in different units. Make sure that all values are converted to the same unit system before performing any calculations. This will help to avoid discrepancies in your results.

Cross-Check with Known Values

If possible, cross-check your results with known values or estimates. For example, if you’re working with a material whose mass and volume are well-known, you can use those values to see if your result aligns with the expected outcome. This can be an effective way to identify potential mistakes.

Use Estimation for Reasonability

For some problems, performing a rough estimation before calculating can help you judge if the final result is reasonable. If your result is drastically different from what you estimated, it may be a sign that an error was made somewhere in your calculations.

Reverse Calculation

Another way to verify your solution is to reverse the calculation. For example, if you calculated the mass from a given volume, you can check your answer by dividing the mass by the volume to see if it gives you the correct value.
This process helps ensure that no mathematical mistakes were made in the earlier steps.

Check for Consistency Across Different Problems

When working on multiple problems, verify that your answers are consistent across similar scenarios. If your solution for one problem differs significantly from others with similar conditions, it may indicate an error in your process.
Reviewing how you approach each type of problem can highlight areas where you need to refine your technique or understanding.

By following these strategies and taking the time to verify your results, you can ensure that your calculations are accurate and that your understanding of the material is solid.

Using the Solution Guide Effectively

When working through problems, it can be tempting to rely on the provided solution guide to check your results. While this can help confirm accuracy, it’s important to use it strategically. The guide should not be a crutch, but rather a tool to enhance your learning and understanding. Here’s how you can make the most of it.

Understand the Step-by-Step Process

Instead of just looking at the final result, carefully examine the process shown in the solution guide. Pay attention to each step and understand why it’s necessary. This approach will help you grasp the underlying principles and allow you to solve similar problems independently in the future.

Identify Mistakes and Learn from Them

If your answer differs from the one in the guide, don’t just move on. Analyze where you might have gone wrong. Compare your work with the provided solution and pinpoint any errors you made in calculations or reasoning. Understanding these mistakes is key to improving your problem-solving skills.

Check for Alternative Methods

Sometimes, the solution guide may present a different method of solving the problem than the one you initially used. Consider exploring these alternative methods, as they may offer deeper insights or more efficient approaches. This broadens your problem-solving toolkit and helps you adapt to various situations.

Reinforce Your Understanding with Practice

The best way to internalize what you’ve learned is through repetition. After reviewing the solution guide, try solving similar problems on your own. Use the guide as a reference to verify your approach and refine your skills rather than relying on it immediately for confirmation.

Use as a Learning Resource, Not a Shortcut

Only consult the solution guide after attempting the problem yourself.
Make sure to fully comprehend each step in the guide before moving on to the next problem.
Employ the guide as a tool for deeper learning, not just for checking final answers.

By following these strategies, you can use the solution guide to strengthen your understanding, avoid repeating mistakes, and become more confident in tackling similar problems independently.