
Understanding advanced problem-solving techniques and mathematical principles is essential for anyone aiming to excel in numerical reasoning. This section focuses on building the skills needed to navigate through various complexities in mathematical exercises.
Here, you’ll find explanations and examples designed to enhance your comprehension of critical topics. By exploring practical methods and insightful strategies, you can improve your analytical abilities and tackle challenges more effectively.
Whether you’re revisiting foundational ideas or exploring new approaches, this guide provides the tools you need to deepen your understanding and perform better in evaluations.
Understanding Key Concepts in Chapter 11
In this section, we explore foundational ideas that will help you strengthen your mathematical reasoning. By grasping these essential principles, you will gain the ability to solve a variety of problems with confidence. Understanding the core concepts is crucial for building a strong mathematical foundation and advancing to more complex topics.
We’ll focus on critical elements such as functions, equations, and graphing techniques that are vital for mastering advanced problem-solving. Familiarity with these concepts allows you to approach exercises with a structured method, improving both accuracy and efficiency.
Grasping the underlying principles will also make it easier to apply theoretical knowledge to real-world scenarios, enhancing your ability to think analytically and creatively in solving mathematical challenges.
Solving Quadratic Equations Effectively
Mastering the process of solving equations with multiple variables and exponents is essential for tackling a wide range of mathematical problems. A deep understanding of the techniques involved allows for quicker, more accurate solutions, which is crucial when faced with more complex scenarios.
One of the most effective methods is factoring, which involves breaking down a complex equation into simpler components. By recognizing patterns and applying appropriate formulas, you can simplify the problem-solving process significantly.
Factoring Method
Factoring requires identifying common factors within the equation, allowing you to separate terms in a way that makes solving easier. Recognizing the structure of quadratic expressions is key to applying this technique successfully.
Quadratic Formula
For situations where factoring isn’t straightforward, the quadratic formula provides a reliable solution. This formula can be used to find the roots of any quadratic equation, making it an invaluable tool for solving complex problems efficiently.
Mastering Exponential Functions for Success
Understanding the behavior of rapidly growing or decreasing quantities is a critical skill in mathematical studies. These concepts are fundamental for interpreting patterns and solving problems related to rates of change, making them essential for both academic and practical applications.
By exploring key properties such as growth, decay, and transformations, you can gain a deeper insight into how these functions work. A solid grasp of these ideas will allow you to approach related problems with confidence and precision.
Understanding Growth and Decay
Growth involves quantities increasing over time, often at an accelerating rate, while decay describes a gradual reduction. Recognizing these trends is vital for solving real-world problems such as population predictions or financial modeling.
Applying Transformations

Transformations, including shifts and stretches, allow you to modify functions to fit specific scenarios. By mastering these techniques, you can adapt and solve a wider range of problems effectively.
Graphing Techniques for Quadratic Functions

Visualizing mathematical relationships through graphs provides a clear and intuitive way to understand the behavior of equations. In particular, graphing functions that involve squared terms can offer insights into their structure and solutions.
Mastering graphing techniques allows you to represent these functions accurately and analyze their key features such as vertex, axis of symmetry, and direction of opening. By employing these methods, you can easily identify the nature of the solutions and their practical significance.
- Identifying Key Points: The vertex, intercepts, and symmetry are the primary points that shape the graph.
- Plotting the Vertex: The vertex is the point where the graph changes direction, providing important information about the function’s minimum or maximum value.
- Determining the Axis of Symmetry: This vertical line divides the graph into two mirror-image halves, making it easier to plot the function accurately.
By following these simple steps, you can quickly sketch and interpret quadratic functions, facilitating easier problem-solving and deeper understanding of mathematical relationships.
Analyzing Real-World Applications of Algebra
Mathematical principles extend far beyond theoretical exercises, offering valuable tools to solve practical challenges encountered in various fields. By applying equations and formulas to everyday situations, we gain insights that can help in decision-making, optimization, and problem-solving across many industries.
Understanding how to use these concepts in real-world scenarios enhances their relevance and utility. Whether in finance, engineering, or science, mathematical models provide effective ways to predict outcomes and create solutions for complex problems.
| Field | Example | Benefit |
|---|---|---|
| Finance | Budgeting and interest calculations | Helps manage expenses and investments |
| Engineering | Structural design and analysis | Ensures safety and efficiency |
| Marketing | Market research and trend analysis | Optimizes advertising strategies |
These examples demonstrate how mathematical methods form the backbone of decision-making processes, offering practical applications that extend beyond the classroom.
Breaking Down Polynomial Expressions
Breaking down complex mathematical expressions into simpler components allows for easier manipulation and understanding of their structure. By analyzing each term and identifying patterns, we can simplify expressions, solve problems more efficiently, and gain deeper insights into the behavior of functions.
When working with these expressions, it’s essential to recognize the different types of terms, their powers, and how they interact. By using systematic approaches like factoring or grouping terms, we can reduce the complexity and arrive at solutions more quickly.
Identifying Key Components
- Terms: Individual parts of an expression separated by addition or subtraction signs.
- Coefficients: Numbers multiplying variables in each term.
- Exponents: Indicate the power to which the variable is raised.
Simplifying Expressions
- Combine like terms by adding or subtracting their coefficients.
- Factor common elements to simplify the expression further.
- Rewrite the expression in its simplest form for easier solving.
By breaking down polynomial expressions into their fundamental parts, you can approach them with confidence and clarity, making problem-solving much more manageable.
Step-by-Step Problem-Solving Strategies
Approaching complex problems methodically can make the process more manageable and less overwhelming. By breaking down each challenge into smaller, logical steps, you can ensure that every aspect is addressed thoroughly, leading to accurate solutions and a better understanding of the concepts involved.
The key to effective problem-solving is to follow a structured approach that helps you stay organized and focused. Each step serves as a building block, guiding you toward the final answer with clarity and precision.
Start by carefully analyzing the problem, identifying the given information, and recognizing what needs to be found. From there, proceed step by step, applying relevant strategies, and checking your work along the way to ensure accuracy.
Common Mistakes to Avoid in Tests
When faced with an assessment, it’s easy to make small errors that can lead to significant consequences. Often, these mistakes result from rushing, overlooking key details, or misinterpreting questions. Recognizing and avoiding these common pitfalls can help improve performance and boost confidence.
By adopting a careful and methodical approach, you can minimize errors and enhance your problem-solving skills. Paying attention to every part of the question and double-checking your work are simple yet effective strategies for success.
Rushing Through Questions
Speed can be a double-edged sword during assessments. While it’s important to manage time effectively, rushing can lead to missed steps or incorrect calculations. Take the time to carefully read each question, and don’t hesitate to pause and think before answering.
Overlooking Key Information
Sometimes, the most critical details are hidden in plain sight. Be sure to carefully review all the provided information, including instructions and numbers, to avoid missing anything important. Taking a moment to re-read each part of the question can make all the difference in achieving a correct solution.
Practical Tips for Factoring Expressions
Factoring expressions can seem like a daunting task, but with the right approach, it becomes much easier. Breaking down complex expressions into simpler components allows for clearer solutions and a deeper understanding of mathematical relationships. By using a few effective strategies, you can enhance your problem-solving ability and streamline the process.
- Look for a common factor: Always start by checking if there’s a number or variable that can be factored out of all terms.
- Use grouping: If the expression has more than two terms, try grouping terms together to find common factors in pairs.
- Recognize special patterns: Look for perfect squares, difference of squares, or other recognizable patterns that can simplify factoring.
- Check for factorable quadratics: If the expression is quadratic, use methods like the AC method or trial and error to find the right factors.
By practicing these techniques, you’ll gain a stronger grasp of how to deconstruct and simplify expressions effectively, leading to quicker and more accurate results.
Importance of Vertex Form in Equations
Understanding the vertex form of equations plays a crucial role in solving and analyzing quadratic relationships. This specific representation helps in identifying key properties, such as the maximum or minimum values, and provides a clear way to graph parabolas. Knowing how to convert from standard to vertex form can simplify both problem-solving and interpretation of mathematical models.
Key Benefits of Vertex Form
- Directly identifies the vertex: The vertex form clearly reveals the coordinates of the vertex, making it easier to graph the equation.
- Reveals the direction of the parabola: The coefficient in the vertex form indicates whether the parabola opens upwards or downwards.
- Helps in finding maximum or minimum values: The vertex represents the highest or lowest point on the graph, which is important in optimization problems.
Applications in Real-World Scenarios
- Modeling projectile motion: In physics, the vertex form can be used to model the trajectory of objects under gravity.
- Optimization problems: In business or economics, vertex form is useful for finding optimal points, such as maximizing revenue or minimizing costs.
Mastering vertex form is essential for analyzing parabolas and applying these concepts effectively in various mathematical and real-world contexts.
Utilizing Graphing Calculators Effectively
Graphing calculators are powerful tools that can significantly aid in visualizing and solving complex mathematical problems. By inputting equations and instantly generating graphs, these devices provide insights that are difficult to achieve through manual methods. Learning how to use them efficiently can enhance your problem-solving skills and improve your understanding of mathematical concepts.
Getting the Most Out of Graphing Features
- Inputting equations: Start by ensuring that you enter equations correctly, paying attention to parentheses and operators to avoid errors.
- Adjusting viewing window: Customize the window settings to ensure that you can view the relevant part of the graph. This is particularly useful for zooming in on key points.
- Analyzing intercepts: Use the calculator’s tools to find x-intercepts, y-intercepts, and other important points on the graph.
Using Additional Functions for Deeper Analysis
- Trace and zoom features: Utilize the trace function to move along the graph and find specific coordinates. Zoom in and out to examine different sections of the graph.
- Graphing inequalities: Many graphing calculators allow you to graph inequalities, helping you visualize solution regions and understand the relationships between variables.
By mastering these functions, you can make the most of your graphing calculator, allowing for quicker and more accurate solutions to a wide range of problems.
Interpreting Results in Mathematical Context

Understanding the results of mathematical operations is crucial for applying them correctly in real-life situations. Once an equation is solved or a graph is generated, it’s important to interpret the findings within the context they are being used. This process allows you to extract meaningful conclusions and make informed decisions based on the data.
For example, when solving for unknowns in word problems, the results must be checked to ensure they make sense in the scenario. Does the solution fit the physical constraints of the problem? If not, further analysis might be needed. Additionally, it’s essential to consider the units of measurement, the scale of the graph, and the range of possible values when interpreting outcomes.
By connecting the mathematical results to real-world situations, one can verify their validity and understand their implications more clearly. This skill is vital for applying mathematical techniques effectively across various fields, from science and engineering to economics and everyday problem-solving.
Tips for Reviewing Study Material
Effective review strategies are essential for mastering any subject and retaining information over time. The key to successful revision lies in not just reading through the material, but actively engaging with it to reinforce your understanding. By using a variety of techniques, you can enhance your ability to recall information and solve problems more effectively.
One powerful method is spaced repetition. This involves reviewing the material at increasing intervals, which helps strengthen memory retention. Another helpful approach is summarizing key concepts in your own words. This forces you to process the information more deeply and ensures that you truly understand the material.
Additionally, practicing with sample problems is a great way to test your comprehension and identify areas where you may need more practice. Organizing your study sessions into manageable chunks and taking regular breaks can also improve focus and prevent burnout.
By combining these strategies, you can ensure that your study time is both productive and efficient, helping you to master the material and perform well when it counts.
How to Approach Complex Algebra Problems
When faced with intricate mathematical challenges, it’s crucial to break them down into simpler components. Rather than attempting to solve the problem all at once, begin by identifying key elements and understand how they relate to one another. This will help in reducing the complexity and providing a clear path towards the solution.
Start by carefully reading the problem. Identify the variables and any given information. Take note of any relationships or constraints that might apply, as these will guide your approach. Next, organize the problem step by step, ensuring that each phase is clear and manageable. This allows you to focus on one part of the problem at a time, reducing the feeling of being overwhelmed.
Another important strategy is to simplify the expressions whenever possible. Factor numbers or combine like terms to make the equation more straightforward. If necessary, apply known formulas or techniques, such as substitution or elimination, depending on the structure of the problem.
Lastly, double-check your work to ensure accuracy. Review each step methodically, looking for potential errors in calculations or logic. This careful, systematic approach will enhance your ability to tackle even the most challenging problems with confidence.
Insights into Quadratic Inequalities
When working with mathematical expressions that involve relationships between variables, understanding how to handle inequalities can be essential. Unlike equations where solutions are specific, inequalities provide a range of values that satisfy the conditions. This can be particularly useful when modeling real-world scenarios where exact values aren’t always required, but rather a range of possibilities.
Graphical Representation of Inequalities
One effective method for solving quadratic inequalities is graphing. The graphical approach allows you to visualize the solution set by identifying the region that satisfies the inequality. By plotting the corresponding quadratic function, you can determine whether the inequality involves values greater than or less than the parabola’s curve.
- Identify the vertex and direction of the parabola.
- Plot the points that represent the boundary of the inequality.
- Shade the appropriate region that satisfies the inequality.
Key Techniques for Solving Inequalities
Several techniques can be used to solve quadratic inequalities algebraically. One common approach is to express the inequality in standard form and then solve for the critical points by finding the roots of the corresponding equation. Once the roots are determined, you can use test points in the different regions to determine which intervals satisfy the inequality.
| Step | Action |
|---|---|
| Step 1 | Rewrite the inequality in standard form. |
| Step 2 | Find the roots of the corresponding equation. |
| Step 3 | Test values in each region to identify the solution set. |
With these techniques, you can confidently approach quadratic inequalities, whether graphically or algebraically, ensuring a deeper understanding of their behavior and applications in various contexts.
Techniques for Simplifying Expressions Quickly
Simplifying expressions efficiently is a crucial skill in mathematics, especially when dealing with complex formulas. By applying systematic strategies, you can reduce intricate problems into manageable forms, which not only saves time but also minimizes the chances of making mistakes. Whether you’re working with polynomials, rational expressions, or other types of mathematical statements, mastering these techniques can help streamline your problem-solving process.
Identifying Like Terms
One of the most effective techniques for simplifying expressions is identifying and combining like terms. Like terms are terms that have the same variable raised to the same power. This step is essential in reducing the complexity of an expression and makes the calculation more efficient.
- Look for terms with identical variables and exponents.
- Add or subtract the coefficients of these terms.
- Rewrite the simplified expression by combining them into one term.
Factoring and Distributive Property
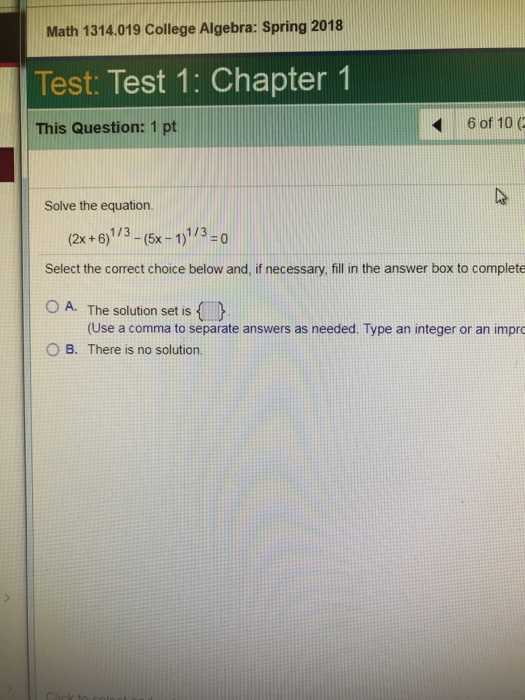
Another important strategy for simplifying expressions involves factoring and applying the distributive property. Factoring allows you to break down complex expressions into simpler components, while the distributive property helps to eliminate parentheses and consolidate terms more efficiently.
| Step | Action |
|---|---|
| Step 1 | Look for common factors within the expression. |
| Step 2 | Factor out the greatest common factor (GCF). |
| Step 3 | Apply the distributive property to expand and simplify. |
By using these techniques, you can quickly and effectively simplify even the most complex expressions, helping you to focus on the overall problem-solving process and achieve accurate results.
Preparing for Test Day with Confidence
Approaching an assessment with confidence starts long before the day itself. Preparing effectively involves organizing study time, managing stress, and practicing the material in a way that builds both skill and self-assurance. By following a structured approach, you can transform anxiety into readiness and tackle challenges with a clear, focused mind.
To set yourself up for success, it’s important to start reviewing the material well in advance. Break down complex concepts into smaller, manageable parts, and focus on one area at a time. Prioritize the topics that are most challenging and make sure to spend extra time reinforcing those. Consistent practice and revisiting difficult sections will enhance your understanding and memory.
Effective Time Management

Efficient time management plays a crucial role in successful preparation. Allocate specific time slots for studying, allowing breaks to avoid burnout. A well-paced study schedule will ensure that you cover all topics without feeling rushed on the day before the assessment.
- Set realistic study goals for each session.
- Use a timer to keep track of study periods and breaks.
- Review your progress periodically to adjust your approach.
Building Mental Readiness
Mental preparation is just as important as academic readiness. On the day before the assessment, make sure to get plenty of rest. A well-rested mind is more focused, alert, and capable of recalling information. Managing stress through relaxation techniques, like deep breathing or visualization, can also enhance concentration.
Approach the assessment with a positive mindset, trusting in the preparation you’ve put in. Confidence doesn’t come from knowing everything, but from being prepared to handle any challenges that arise. With the right mindset and solid study habits, you’ll approach the test with the assurance that you can perform at your best.