CPM Core Connections Geometry Answer Key Guide

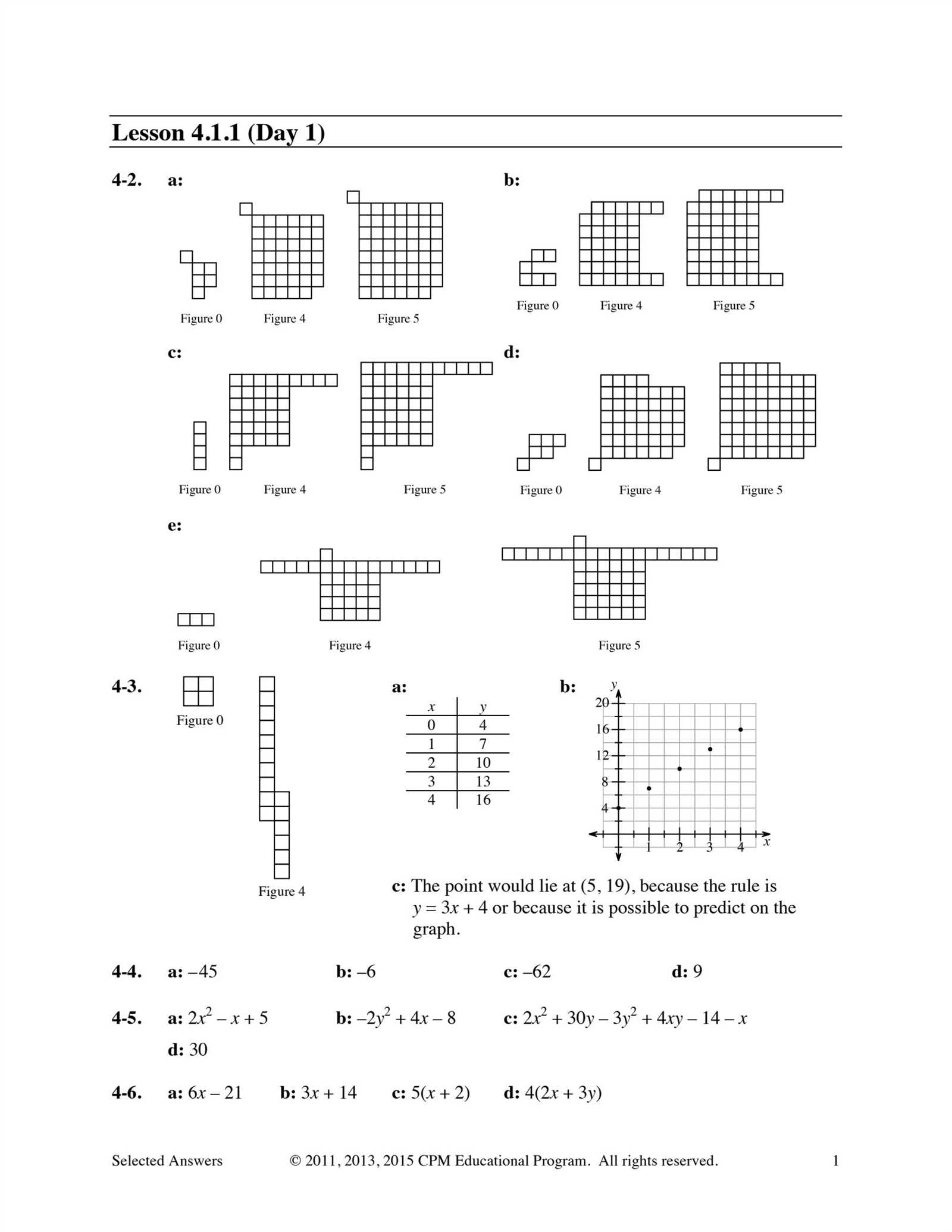
Mastering complex mathematical concepts requires more than just memorizing formulas; it involves understanding the fundamental principles behind each problem. By focusing on structured learning methods, students can develop the skills needed to tackle a wide range of challenges. This section aims to guide learners through essential techniques that enhance comprehension and improve performance.

With the right approach, finding solutions to various mathematical exercises becomes a systematic process. Resources designed to support this journey can offer detailed explanations and step-by-step instructions. Whether you’re practicing on your own or reviewing a specific task, these materials provide valuable insight into the methodology that will help you succeed.

Success in mathematics often lies in the ability to break down problems into smaller, more manageable parts. Using available resources effectively allows for a deeper understanding and better application of key concepts. By exploring this section, students will gain the confidence to approach even the most challenging topics with clarity and focus.

CPM Core Connections Geometry Overview

Understanding mathematical reasoning and applying it to solve problems is at the heart of learning. This section provides an introduction to the principles and techniques used in mathematical exercises designed to enhance problem-solving abilities. By breaking down key concepts into digestible steps, students can navigate through complex tasks more effectively.

Fundamental Learning Approach

The focus is on mastering the building blocks of mathematical concepts. As students progress, they gain a clearer understanding of how to approach various exercises. The main goal is to develop a strong foundation that makes more advanced topics easier to grasp. Some essential elements of this process include:

Breaking down problems into simpler components
Applying structured methods to understand relationships
Identifying patterns and using them to find solutions
Encouraging consistent practice to reinforce knowledge

How Materials Support the Learning Process

To effectively solve problems, learners need clear resources that guide them through each stage. These tools offer organized explanations that demonstrate how to tackle a variety of challenges. With dedicated practice, students can improve their skills and gain the confidence to handle more intricate tasks. The materials available include:

Step-by-step instructions that clarify complex topics
Examples that illustrate proper problem-solving techniques
Solutions that highlight the correct methods for tackling exercises

By using these resources thoughtfully, students will be able to strengthen their mathematical abilities and build the knowledge necessary to succeed in future learning endeavors.

Understanding Geometry Core Concepts

To excel in mathematical studies, it is essential to comprehend the foundational principles that guide problem-solving in spatial reasoning. This section focuses on the fundamental ideas that serve as the building blocks for more complex concepts. By grasping these core elements, students can approach mathematical challenges with a structured mindset, making even difficult problems more manageable.

Key Principles in Spatial Reasoning

Mathematical reasoning involves understanding relationships between shapes, angles, and sizes. Recognizing these relationships is crucial for solving a wide range of tasks. Some of the fundamental principles include:

The properties of different shapes and their characteristics
The concept of measurements, such as length, area, and volume
The use of angles and their significance in solving problems
The relationship between various geometric objects and their interactions

Building a Strong Foundation

By establishing a strong understanding of these basic concepts, learners are better equipped to solve more complex problems. Mastery of these essential principles ensures a smoother progression to advanced topics. This understanding also helps in visualizing problems, which is a key skill for success in more complex applications. Effective learning strategies include:

Regularly reviewing foundational concepts to solidify knowledge
Applying concepts to real-world situations for better understanding
Using visual aids and diagrams to represent problems

With a firm grasp of these core principles, students will develop the confidence to tackle progressively more intricate challenges in their mathematical studies.

How to Use the Answer Key

To effectively navigate through mathematical exercises, it’s important to understand how to utilize provided solutions to improve learning. A well-structured solution guide offers more than just the final answers; it helps clarify the methods used to arrive at the solutions, providing insight into the problem-solving process. Learning to use this resource correctly can significantly enhance your understanding of the material and improve overall performance.

Instead of simply copying the provided answers, focus on analyzing the steps involved. By reviewing each step carefully, you can identify the reasoning behind the solution and apply similar techniques to other problems. This approach encourages deeper learning and helps reinforce the concepts being studied.

Key strategies for using the solution guide include:

Reviewing each step to understand the logic behind the solution
Comparing your approach with the provided steps to identify areas for improvement
Using the solutions as a tool for self-assessment and reflection
Practicing similar problems independently before consulting the guide

By following these strategies, you can maximize the benefit of the solution guide and strengthen your problem-solving skills. This approach allows you to develop a deeper understanding of the subject and gain confidence in tackling similar tasks in the future.

Key Geometry Topics in CPM

Mastering mathematical concepts requires understanding essential topics that form the foundation of more complex problems. In this section, we focus on the most important areas of study, which are critical for building a strong knowledge base. These topics are central to developing the skills needed to approach various exercises with confidence and precision.

Foundational Concepts in Spatial Relationships

To effectively solve problems, it is crucial to first understand the fundamental relationships between different shapes and figures. This includes studying their properties, sizes, and how they interact. Some core areas to focus on are:

Properties of different shapes (triangles, quadrilaterals, circles)
Understanding angles and their types (acute, right, obtuse)
The concept of symmetry and transformations (reflection, rotation, translation)
Measurement techniques (length, area, perimeter, volume)

Advanced Problem-Solving Techniques

Once the foundational concepts are mastered, students can explore more advanced methods of tackling problems. This includes working with complex figures, applying theorems, and using algebraic approaches to solve geometric puzzles. Some advanced topics to study include:

Using the Pythagorean theorem for right triangles
Understanding trigonometric ratios (sine, cosine, tangent)
Exploring coordinate geometry for graphing shapes and finding distances
Solving real-world problems using geometric reasoning

Focusing on these key areas provides a comprehensive understanding and prepares learners for higher-level challenges in mathematics.

Mastering Core Connections with Practice

Achieving proficiency in mathematical concepts is a gradual process that requires consistent effort and practice. By regularly engaging with exercises, students can reinforce their understanding and improve their problem-solving skills. The key to mastering any topic is not just understanding the theory but also applying it repeatedly through various challenges.

Regular practice helps to solidify knowledge and build confidence. It encourages learners to approach problems from different angles and develop strategies that lead to efficient solutions. Over time, this consistent exposure helps students internalize core principles and apply them effectively in real-world situations.

Some effective ways to practice and enhance your skills include:

Solving a variety of problems to cover different topics and techniques
Reviewing mistakes to understand where errors occurred and how to avoid them
Challenging yourself with problems of increasing complexity to build confidence
Collaborating with peers or seeking feedback to improve your approach

By incorporating these strategies into your study routine, you will strengthen your understanding and develop the skills necessary for tackling even the most challenging exercises.

Strategies for Geometry Problem Solving

Effective problem solving in mathematics requires more than just following steps; it involves applying logical reasoning, recognizing patterns, and utilizing the right techniques for each task. By developing a range of strategies, students can approach challenges with confidence and efficiency. In this section, we explore key approaches that can make tackling complex exercises easier and more intuitive.

One of the most important strategies is breaking problems down into smaller, manageable parts. By focusing on one element at a time, students can simplify complex scenarios and reduce the likelihood of errors. Another effective method is visualizing the problem, which can provide a clearer understanding of spatial relationships and help to identify potential solutions.

Some other valuable techniques for solving problems include:

Drawing diagrams or sketches to represent the given information
Looking for patterns or symmetries that simplify the problem
Using known formulas or theorems to connect different parts of the problem
Working backwards from the desired solution to uncover missing details
Checking calculations at each step to ensure accuracy

By consistently applying these strategies, learners can improve their ability to solve even the most challenging problems with greater ease and precision.

Common Mistakes to Avoid in Geometry

Mathematical problem-solving can be challenging, and even the most experienced students can fall into common traps. Recognizing and avoiding these mistakes is a crucial part of mastering the subject. By being mindful of typical errors, learners can improve their accuracy and approach tasks with greater confidence.

Overlooking Key Details

One of the most frequent mistakes is overlooking important information in a problem. Students may rush through the problem and miss crucial data that affects the solution. This can lead to incorrect results or missed steps. To avoid this mistake:

Always read the problem carefully and underline or highlight key information
Double-check the conditions or constraints provided in the task
Make sure all variables are clearly defined before proceeding with calculations

Incorrect Application of Formulas

Another common error is using the wrong formula or applying it incorrectly. Many concepts rely on specific formulas, and misapplying them can lead to serious mistakes. To ensure proper application:

Review the relevant formulas and understand when and how to use them
Check if the given problem aligns with the formula you are applying
Ensure all values are correctly substituted into the formula

By focusing on accuracy and understanding the fundamental concepts, students can minimize these mistakes and strengthen their problem-solving skills.

Essential Tools for Geometry Success

Achieving success in mathematical studies requires more than just understanding concepts; it also involves using the right tools to help visualize, measure, and solve problems effectively. Having the right resources at your disposal can significantly enhance your ability to approach challenges with confidence. In this section, we’ll explore some of the key tools that are essential for mastering mathematical tasks.

These tools not only assist in solving problems but also foster a deeper understanding of spatial relationships, measurements, and theorems. Whether you are working on basic exercises or complex scenarios, the following resources are indispensable for your success:

Scientific Calculator: A calculator helps with complex arithmetic, trigonometry, and algebraic calculations, allowing you to focus on problem-solving rather than manual computations.
Graph Paper: Using graph paper helps to visualize geometric figures and plot points accurately, which is especially useful when dealing with shapes and coordinates.
Ruler and Compass: These basic tools are essential for drawing accurate lines, angles, and shapes, ensuring precision in construction tasks.
Protractor: A protractor allows you to measure angles precisely, an essential skill for many geometric calculations.
Geometry Software: Digital tools and apps can be useful for exploring shapes and figures in a virtual space, allowing for easy experimentation and manipulation.

By using these tools effectively, students can improve their accuracy, enhance their problem-solving abilities, and deepen their understanding of mathematical principles. Incorporating these resources into your study routine will undoubtedly set you up for success in this subject.

Tips for Efficient Study and Review

Effective studying and reviewing require not only dedication but also strategic planning. By adopting smart techniques, learners can make the most of their time and improve retention, leading to better results. In this section, we will discuss several methods that can help optimize your study sessions and enhance your understanding of challenging material.

Rather than cramming all at once, it is important to study consistently and review regularly. Spacing out learning sessions allows for better long-term retention. Additionally, focusing on key concepts and tackling difficult areas first will maximize productivity. Below are some practical strategies to help you make the most of your study time:

Active Recall: Instead of passively reading through notes, try to actively recall key points and concepts from memory. This strengthens neural connections and improves understanding.
Practice Regularly: Consistent practice helps reinforce knowledge and identify areas needing further review. Solve a variety of problems to ensure comprehensive mastery.
Use Study Guides: Summarize key concepts in your own words, creating personalized study guides. This reinforces learning and makes reviewing more efficient.
Group Study Sessions: Collaborating with peers can help clarify confusing topics, as discussing different approaches can lead to deeper insights.
Take Breaks: Avoid burnout by taking short breaks between study sessions. This helps maintain focus and prevent fatigue.
Teach Someone Else: Explaining complex concepts to others forces you to solidify your understanding and identify any gaps in knowledge.

By incorporating these strategies into your routine, you can study more effectively and ensure that your preparation is both thorough and efficient. Consistency, focus, and smart techniques will make a significant difference in your learning outcomes.

What to Expect from Geometry Assessments

Mathematical evaluations are designed to measure how well you understand the principles and techniques learned throughout the course. These assessments typically test your ability to solve problems, apply theoretical concepts, and demonstrate proficiency in various mathematical skills. Knowing the structure of these evaluations and the types of questions you may encounter can help you approach the test with more confidence and readiness.

During a mathematical assessment, you can expect a range of questions that challenge different aspects of your knowledge. The questions may involve calculations, logical reasoning, and real-life problem applications. You’ll be required to work through problems involving shapes, measurements, and the relationships between different geometric figures. Understanding these concepts is key to achieving success on the test.

Here are some common features of mathematical assessments:

Conceptual Questions: Expect questions that assess your understanding of fundamental principles like properties of shapes, angles, and symmetry.
Problem-Solving Tasks: These questions may involve complex scenarios where you must apply multiple concepts to arrive at a solution, often requiring critical thinking and analysis.
Diagrams and Visuals: Many questions include diagrams or visual aids that you must interpret, helping to assess your ability to apply geometric reasoning.
Time Constraints: The assessment will likely be timed, so practicing problem-solving under time limits will help you become more efficient at managing your time during the test.

Understanding the structure of the assessment and the types of questions you may face allows you to focus on your studies and approach the test with confidence. Preparation and consistent practice are essential to mastering the material and performing well in these evaluations.

How Geometry Answers are Structured

Mathematical solutions require a clear, logical approach that demonstrates not only the final result but also the reasoning behind it. Whether you are solving for a specific value, proving a property, or explaining a relationship, the structure of your solution is crucial in conveying your thought process. A well-structured solution helps to make your reasoning transparent, allowing others to follow your approach and understand how you reached your conclusion.

In most cases, answers are broken down into several key components to ensure clarity and precision. A typical solution involves a series of steps that are logically connected, often accompanied by supporting calculations, visual aids, or reasoning. Here’s how answers are usually structured:

Step-by-Step Solution Process

Each problem is typically approached in a sequence of steps. These steps help to methodically tackle the problem, ensuring that all aspects are covered.

Identifying Known Information: The first step involves listing all given data or known values that will help in solving the problem.
Defining the Goal: The next step is to clearly understand and define what needs to be found or proven.
Applying Relevant Concepts: This involves using appropriate formulas, theorems, or principles to start working through the problem.
Calculation and Reasoning: As you work through the problem, show all calculations and reasoning to ensure the solution is clear and verifiable.
Final Result: Conclude by providing the final value or proof, ensuring that it directly answers the problem posed.

Visual Aids and Diagrams

Many mathematical solutions require visual representation. Diagrams or graphs are often included to illustrate the relationships between different elements and provide a clearer understanding of the problem. These visuals help to reinforce the steps and aid in identifying key relationships or patterns.

By following this structured approach, you can present your solutions in a clear and logical manner, making it easier to demonstrate your understanding and ensure your answers are easily interpreted.

Learning Geometry Through Core Connections

Understanding the fundamental principles of shapes, measurements, and spatial relationships requires a structured approach. Learning the various aspects of mathematics through interconnected ideas helps build a deeper understanding and facilitates the application of concepts in more complex scenarios. By linking new information to what is already known, learners are able to see patterns and gain insights that make problem-solving easier and more intuitive.

The process of learning through interconnected ideas involves several key steps that integrate new knowledge with existing skills. This method not only enhances comprehension but also promotes retention, as each concept reinforces the other. By applying what you’ve learned in different contexts, you can approach problems from multiple angles, increasing both flexibility and confidence.

Building Understanding through Progressive Learning

One of the key strategies in mastering this approach is starting with foundational concepts and gradually building upon them. This ensures that each new idea is rooted in what has already been established. Here’s how this method works:

Starting with Basics: Begin with core principles and definitions that lay the groundwork for more complex topics.
Layering Knowledge: As you become comfortable with initial concepts, expand your knowledge by incorporating more advanced ideas that build on these basics.
Problem Application: Use practice problems to apply new knowledge and deepen your understanding of how different concepts relate to one another.
Reinforcement through Review: Regularly review and revisit concepts to solidify your understanding and identify any gaps in knowledge.

Connecting Concepts for Real-World Application

Learning through this interconnected approach also helps in applying abstract ideas to real-world problems. By seeing how geometric principles relate to various fields, such as architecture, engineering, and design, students gain a better appreciation for the subject’s practical applications. This encourages not only theoretical understanding but also practical problem-solving skills, enabling learners to transfer their knowledge to various contexts.

Through this method, the study of mathematics becomes more engaging, relevant, and accessible. It fosters critical thinking and prepares learners to tackle a wide range of challenges, both academic and real-world.

Maximizing Your Understanding of Geometry

Achieving mastery in the study of shapes, spatial relationships, and mathematical reasoning requires more than just memorizing formulas or procedures. It involves developing a deep, conceptual understanding of the subject matter. By focusing on foundational concepts and building a clear connection between theory and application, learners can gain a solid grasp of the material, making it easier to tackle more complex problems and think critically about mathematical challenges.

One of the most effective ways to deepen your understanding is through active engagement with the material. This means not only reviewing examples but also practicing consistently, reflecting on mistakes, and seeking out connections between various topics. By embracing a more holistic approach, you can maximize your understanding and improve your problem-solving abilities.

Active Learning Strategies

To maximize your understanding of mathematical concepts, consider incorporating the following strategies into your study routine:

Hands-On Practice: Regularly solving problems allows you to apply what you’ve learned and identify areas for improvement. The more you practice, the more intuitive concepts become.
Break Down Complex Problems: Instead of rushing to find a solution, break down larger problems into smaller, more manageable parts. This helps in understanding the underlying principles behind each step.
Seek Connections: Look for ways in which different ideas within the subject are related. Understanding how one concept builds upon another can provide deeper insights and aid in retention.
Review Mistakes: Mistakes are often the best learning opportunities. When you make an error, take the time to understand what went wrong and how to correct it.

Building Long-Term Understanding

For lasting success, it’s important to focus on both short-term comprehension and long-term retention. This can be achieved through continuous review and reinforcement. Try these approaches to ensure that your understanding evolves over time:

Consistent Review: Periodically revisit concepts to solidify your understanding and ensure retention. This also helps keep previously learned material fresh in your mind.
Teach Others: Explaining concepts to others is a powerful tool for reinforcing your own understanding. If you can teach someone else, it means you truly grasp the material.
Explore Real-World Applications: Consider how the material applies to real-world situations. By connecting abstract concepts to practical use cases, you gain a deeper appreciation for the subject.

By adopting these strategies, you can ensure a comprehensive and thorough understanding of the material, ultimately leading to greater success in both academic settings and beyond.

How Answer Keys Improve Problem-Solving Skills

Using solution guides effectively is a powerful way to enhance problem-solving abilities. These resources provide detailed solutions, which not only help learners check their work but also offer insights into the reasoning and methods behind each step. Understanding how and why certain techniques are applied helps reinforce concepts and fosters a deeper comprehension of the material. This process allows students to identify their mistakes and learn from them, improving both their skills and confidence in tackling similar challenges in the future.

When learners work through problems and then compare their approach to the provided solutions, they can see the logical steps taken and recognize where they might have gone wrong. This reflection is crucial for refining problem-solving strategies and building a more methodical approach. Over time, this practice can help develop a clearer, more efficient problem-solving process.

Benefits of Using Solution Guides

Here are some key advantages of using solution guides to improve problem-solving abilities:

Benefit	Description
Identifying Mistakes	Solution guides help highlight areas where errors may have occurred, allowing learners to correct misconceptions and understand the correct reasoning.
Clarifying Concepts	Detailed solutions often break down complex concepts, making them easier to understand and reinforcing the overall learning process.
Learning Efficient Methods	By examining efficient problem-solving techniques in the solution guide, learners can adopt more streamlined approaches to future problems.
Boosting Confidence	Seeing the correct methods and solutions boosts learners’ confidence, as they can be sure they are progressing in the right direction.
Encouraging Self-Reflection	Solution guides promote critical thinking and reflection, encouraging students to think about their approach and how they can improve their strategies.

By consistently using solution guides as a tool for self-assessment and learning, students can strengthen their problem-solving skills and develop a more effective approach to solving challenges across a variety of subjects.

Benefits of Using the Solution Guide

Utilizing solution resources effectively can significantly improve a learner’s understanding and performance in problem-solving tasks. By reviewing correct solutions, students gain insight into the logical steps required to arrive at the correct answer. This process not only helps verify the accuracy of their work but also provides an opportunity to learn from mistakes and refine techniques. Over time, using these tools can help solidify concepts and improve problem-solving strategies.

One of the key advantages of referring to these solutions is the ability to identify and correct errors. By comparing one’s approach with the correct method, students can pinpoint where they went wrong and learn how to approach similar problems more efficiently. Additionally, it allows learners to adopt better problem-solving habits, making the process faster and more accurate.

Key Benefits of Using Solution Guides

Here are some of the main advantages of using solution resources to enhance your learning:

Benefit	Description
Clarification of Concepts	Reviewing detailed solutions helps clarify complex concepts, allowing students to better understand the steps involved and why certain methods work.
Error Identification	By comparing their own solutions with those in the guide, learners can quickly identify mistakes and learn how to fix them, preventing future errors.
Improvement of Critical Thinking	These guides encourage students to analyze different problem-solving techniques, improving their ability to think critically and approach new challenges with confidence.
Development of Better Strategies	By reviewing correct methods, students can adopt more efficient strategies for solving problems in the future, increasing their overall effectiveness.
Boosting Confidence	When learners see their solutions align with the correct answers, they gain confidence in their abilities, motivating them to tackle more complex problems.

Incorporating these solution guides into the learning process provides an invaluable tool for mastering problem-solving. Whether for reinforcing current knowledge or exploring new concepts, the benefits of using solution resources cannot be overstated. They offer a structured way to improve skills and develop a deeper understanding of the material.

Common Challenges and Solutions in Mathematical Problem Solving

In the world of mathematical problem-solving, there are several challenges that students commonly face. These hurdles often arise when dealing with complex shapes, formulas, or abstract concepts that require deep understanding and practice. However, recognizing these challenges and knowing how to overcome them is key to improving one’s ability to solve such problems effectively. Below, we explore some of the most frequent obstacles and the corresponding strategies that can help learners overcome them.

Common Challenges and How to Overcome Them

Challenge	Solution
Misunderstanding of Theorems	Breaking down theorems into smaller, more manageable parts can help students understand their application. Practice through examples is also effective in clarifying these concepts.
Difficulty in Visualizing Problems	Drawing diagrams or using physical models to visualize the shapes and relationships involved can greatly improve understanding. Digital tools and interactive programs can also assist in visualizing abstract concepts.
Errors in Calculation	Double-checking each step of the calculation process and reviewing mathematical operations ensures fewer mistakes. Using estimation to verify results can also help identify discrepancies.
Inability to Link Concepts	To address this, learners can focus on understanding the connections between different concepts. Revisiting previous topics and exploring their relationship to current problems often provides clarity.
Lack of Practice	Regular practice with a variety of problems enhances proficiency. Working through problems from different areas helps solidify skills and builds confidence in applying different methods.

By addressing these common challenges with targeted solutions, learners can build a stronger foundation for tackling more advanced problems. Through consistent effort and the use of effective strategies, anyone can improve their problem-solving abilities and gain a deeper understanding of complex concepts.