Algebra Nation Test Yourself Section 3 Answers Guide

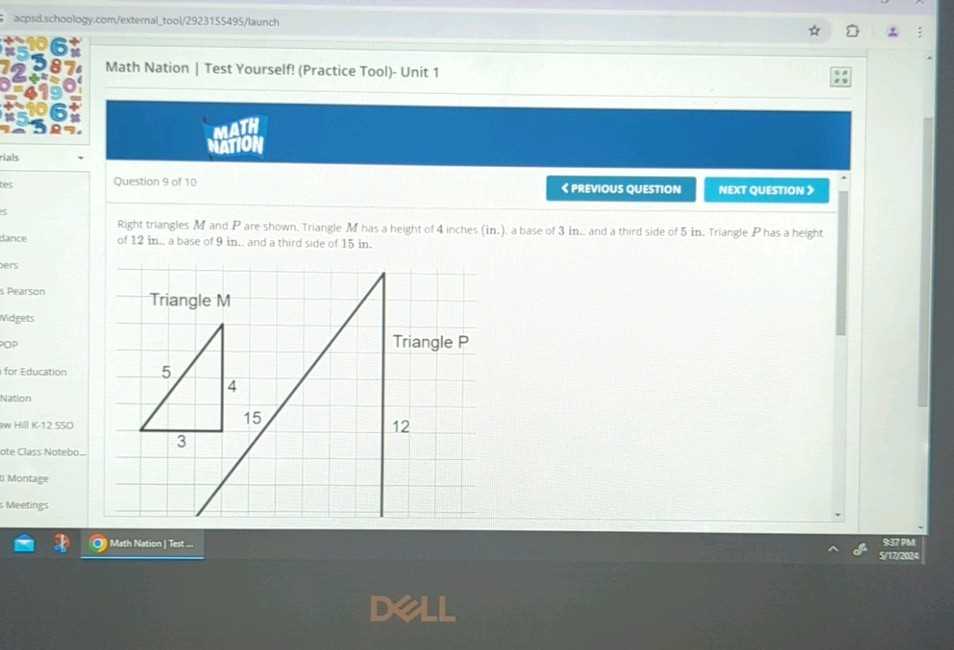
The journey of mastering complex mathematical concepts often starts with structured exercises that challenge your understanding. These activities are designed to push your skills and enhance your problem-solving abilities. Each task presents unique challenges that help solidify your foundation in mathematical theory.

Within this particular set of exercises, a variety of problems are presented, each carefully crafted to test your proficiency in handling different mathematical situations. The goal is not just to find the correct solution but to approach each problem methodically, breaking it down step by step.

Success in these tasks relies on your ability to recognize patterns, apply learned techniques, and think critically. With practice, the skills you develop here will serve as a strong base for tackling even more advanced topics in mathematics.

By revisiting these exercises regularly, you can track your improvement and gain confidence in your abilities. Understanding the process of solving these problems will help you not only in similar tasks but also in other areas of your academic and professional life.

Algebra Nation Test Yourself Section 3 Overview

This segment is designed to challenge your mathematical knowledge with a series of exercises focused on fundamental problem-solving techniques. It emphasizes practical application, pushing you to think critically and strategically as you work through each task. The problems vary in difficulty, testing your grasp of key concepts and methods.

Structure of the Exercises

The tasks are organized in a way that allows you to gradually build your skills. Each problem presents a new challenge, moving from simpler to more complex scenarios, enabling you to track your progress effectively. To help you better understand how these exercises are structured, the table below summarizes the different types of questions you will encounter.

Type of Problem	Difficulty Level	Focus Area
Basic Equation Solving	Easy	Linear Equations
Word Problems	Medium	Application of Concepts
Advanced Problem Solving	Hard	Complex Equations

Key Learning Outcomes

By completing this portion, you will strengthen your ability to approach and solve problems logically. The exercises are crafted to boost your confidence in applying learned strategies in new situations, ensuring a deeper understanding of core principles. Regular practice will not only enhance your skills but also prepare you for more challenging mathematical tasks ahead.

Key Strategies for Solving Algebra Problems

Effective problem-solving requires more than just knowledge of techniques; it involves applying those techniques strategically to arrive at the correct solutions. Whether you are dealing with equations, expressions, or word problems, a methodical approach can significantly improve your efficiency and accuracy. Developing a clear strategy for tackling each type of problem is essential for success.

Understanding the Problem

Before jumping into solving any mathematical task, it’s crucial to fully understand the problem. Read the problem statement carefully and identify what is being asked. Highlight key information and make note of any constraints or special conditions that may influence the solution. Taking a moment to organize your thoughts will help you avoid unnecessary mistakes.

Breaking Down the Problem

Once you understand the problem, breaking it down into smaller, more manageable parts is an effective strategy. If the problem involves multiple steps, solve each part one at a time. Start with simpler tasks and gradually build toward the more complex parts. This approach will keep you focused and reduce the risk of missing crucial steps.

Using elimination and substitution methods can help simplify complicated tasks. These techniques allow you to reduce the number of variables and make the solution more straightforward. Practice applying these methods regularly to gain confidence in solving more complex problems.

Check your work at each stage to ensure that your calculations are accurate. Revisiting each step helps identify errors early, allowing you to correct them before moving on to the next part of the problem.

How to Approach Section 3 Questions

When faced with a series of mathematical challenges, it’s important to develop a clear approach to solve each problem effectively. Breaking down each task into smaller, more manageable parts will help you stay focused and organized. Begin by understanding the problem, then systematically apply your knowledge to arrive at the correct solution.

Start by reading the question carefully, identifying key variables, and understanding what is being asked. Make sure to note any important details, such as constraints or specific conditions, that may affect the outcome. Once you have a clear grasp of the problem, determine which mathematical principles or techniques are best suited for solving it.

Next, solve the problem step by step. Don’t rush through the process; instead, focus on each part individually to ensure accuracy. If the problem involves multiple variables, consider using methods like substitution or elimination to simplify the equation. Always check your work at each stage to avoid mistakes and ensure the solution is correct.

Finally, practice is key. The more you work through similar problems, the more efficient you’ll become at recognizing patterns and applying the right strategies. With time, solving these types of problems will become second nature, helping you build confidence and improve your overall performance.

Common Mistakes in Algebra Nation Tests

Even experienced learners can make errors when solving mathematical challenges. These mistakes often stem from overlooked details, rushed calculations, or misunderstanding key concepts. Identifying and addressing these common pitfalls will improve accuracy and confidence when tackling similar problems in the future.

One of the most frequent errors occurs when the problem is not fully understood before attempting a solution. It’s easy to jump into solving a question without carefully reading the instructions or identifying the crucial elements. Here are some of the most common mistakes:

Rushing through calculations: Many errors arise from hasty computations. It’s important to take your time to avoid simple arithmetic mistakes.
Misinterpreting the question: Sometimes, the wording of a problem can be tricky. Failing to correctly identify what is being asked can lead to incorrect solutions.
Overlooking key details: Key values, constraints, or units of measurement are sometimes missed, affecting the entire approach to the solution.
Skipping intermediate steps: Trying to jump directly to the final answer without working through each step can result in mistakes or oversights.
Incorrect sign handling: Neglecting to properly manage negative signs, especially when working with multiple terms, is a common mistake that can lead to wrong results.
Failure to check the answer: After completing a problem, it’s easy to assume the result is correct. However, reviewing your work can often catch unnoticed errors.

By avoiding these common mistakes, you can improve your performance and become more efficient at solving mathematical challenges. Taking the time to carefully read, calculate, and check your work will ultimately lead to better outcomes and a deeper understanding of the concepts involved.

Improving Accuracy with Practice

Achieving precision in mathematical problem-solving is a skill that improves over time with consistent practice. By repeatedly working through exercises, you can strengthen your ability to approach problems methodically and avoid errors. The more you practice, the more you develop a deeper understanding of key techniques and become familiar with common pitfalls.

Building Confidence Through Repetition

Repetition plays a critical role in reinforcing mathematical concepts. By solving problems of varying difficulty, you train your mind to recognize patterns, identify efficient methods, and develop a keen eye for detail. Each time you practice, you enhance both your speed and accuracy, gradually reducing the chances of making mistakes.

Strategies for Effective Practice

To get the most out of your practice, it’s important to focus on both the quality and variety of problems you solve. Challenge yourself with different types of problems, ensuring you cover a wide range of topics. Focus on areas where you typically struggle, and break down complex problems into smaller, more manageable steps. This focused approach will lead to steady improvement and greater accuracy in your solutions.

Understanding Algebraic Expressions in Section 3

Grasping the structure and components of mathematical expressions is essential for solving more complex problems. An expression involves variables, constants, and operations that work together to represent a mathematical relationship. Understanding how these elements interact is key to simplifying and solving problems efficiently.

In this part of the exercises, you’ll encounter various expressions that require you to apply the correct operations in the right order. Recognizing the importance of parentheses, exponents, and the correct order of operations will help you avoid mistakes and make your solutions more accurate. The goal is not just to solve the problem, but to truly understand how the parts of the expression fit together.

By practicing with different types of expressions, you will develop a stronger understanding of their structure. This foundation will allow you to tackle more advanced problems with greater ease and confidence, ensuring that you can manage even the most complex equations with clarity and precision.

Step-by-Step Guide to Algebraic Solutions

Breaking down mathematical problems into clear, manageable steps is crucial for finding the correct solution. By following a logical sequence, you can avoid confusion and minimize errors. This approach not only ensures accuracy but also helps you better understand the underlying concepts involved.

The process typically begins with identifying the variables and constants in the problem, followed by applying appropriate operations. Each step should be completed carefully, checking for errors before moving on to the next. Below is a simple guide to follow when solving algebraic tasks.

Step	Description
Step 1	Read the problem carefully and identify the unknowns, constants, and operations involved.
Step 2	Simplify the equation by removing unnecessary terms or factoring when needed.
Step 3	Apply the correct operations (addition, subtraction, multiplication, or division) in the right order, following the principles of mathematics.
Step 4	Check each step for accuracy before proceeding to ensure no mistakes have been made.
Step 5	Finally, solve for the unknown variable and review the solution to confirm it meets the conditions of the problem.

By consistently following these steps, you will develop a systematic approach that increases your efficiency and minimizes the likelihood of errors. This methodical practice is key to mastering mathematical concepts and improving your problem-solving abilities over time.

Tips for Time Management During Tests

Effective time management is crucial when faced with a series of problems under a time constraint. The ability to pace yourself and allocate time wisely can greatly impact your performance. By adopting specific strategies, you can avoid rushing and ensure that you have enough time to complete each task accurately.

Prioritize and Plan

Before diving into solving the problems, take a moment to scan through the entire set of questions. This initial overview allows you to get a sense of the difficulty and the time required for each one. Prioritize questions based on their complexity and the time they may take to solve.

Start with easier questions: These will help you gain momentum and secure quick points.
Leave difficult questions for later: Tackle harder problems after addressing the simpler ones to avoid getting stuck.

Set Time Limits

Allocate a specific amount of time to each problem or set of problems. Setting limits will help you stay on track and prevent spending too much time on a single task. If you find yourself stuck on a question, move on to the next one and return later with a fresh perspective.

Break down the time: Divide the total available time by the number of problems to determine how much time to spend on each.
Use a timer: Set a timer for each section or question to ensure you don’t exceed the allotted time.

By following these time management tips, you’ll be able to maximize your efficiency, reduce stress, and increase your chances of completing all tasks within the given time frame.

Reviewing Solutions from Algebra Nation

Analyzing your solutions after completing a problem set is an essential step in the learning process. By reviewing your work, you can identify mistakes, reinforce your understanding, and improve your problem-solving strategies. This process allows you to refine your approach and ensures that you’re not just finding the right answers but also understanding the reasoning behind them.

When revisiting solutions, it’s important to focus on both the accuracy and the methodology. Did you follow the correct steps? Were there any assumptions that led you down the wrong path? By asking these questions, you can gain a deeper understanding of your thought process and make adjustments where necessary.

Here are some key points to consider when reviewing your solutions:

Check for computational errors: Ensure all arithmetic and operations were performed correctly, especially under time constraints.
Review your approach: Did you apply the appropriate method or formula for the problem? Reflect on whether there was a more efficient solution.
Understand each step: Go over each step and verify that it logically follows from the previous one. This reinforces the thought process behind the solution.

By consistently reviewing your work, you can build stronger mathematical skills and prevent recurring mistakes. This habit will contribute significantly to your success in future problem-solving challenges.

How to Check Your Work Effectively

Ensuring the accuracy of your solutions is crucial for success. Reviewing your work allows you to identify errors, validate your approach, and ensure that your conclusions are correct. Checking your work thoroughly can prevent small mistakes from undermining your overall performance and deepen your understanding of the concepts involved.

When reviewing your work, it is important to approach it systematically. Start by verifying each step and making sure it logically follows from the previous one. Look for any inconsistencies or calculations that don’t make sense. It’s also helpful to revisit the problem’s original conditions to ensure your solution fully addresses the question posed.

Here are some strategies to effectively check your work:

Re-read the problem: Make sure you understand what is being asked. Sometimes mistakes occur simply because the problem was misinterpreted.
Rework the problem: Solve the problem again from scratch, either mentally or on paper. This helps verify the result and the steps used to reach it.
Double-check your calculations: Go through each operation and calculation carefully to ensure no arithmetic mistakes were made.
Use reverse operations: If possible, check the final solution by reversing the steps you used to solve the problem (e.g., substituting your answer back into the original equation).

By adopting these checking strategies, you can ensure that your work is accurate and that you are truly grasping the material. This habit of careful review will not only improve your current performance but also strengthen your problem-solving skills in the long run.

Analyzing the Most Challenging Questions

Some problems can be particularly difficult, often due to complex steps or unexpected twists in the problem-solving process. It’s essential to break down these challenging questions to understand where difficulty arises and develop strategies to tackle similar problems in the future. By dissecting these questions, you can identify key areas for improvement and refine your approach to problem-solving.

Breaking Down Complex Problems

When faced with a challenging question, the first step is to analyze it in parts. Look at the information provided and identify what is being asked. Often, the complexity lies in understanding how different pieces of information are related. Simplifying the problem step by step can make it more manageable.

Identify key information: Underline or highlight the crucial details that are central to solving the problem.
Separate the operations: Break down the problem into smaller, more manageable operations or steps.
Look for patterns: Identifying patterns or common structures in the question may help you find a more efficient method for solving it.

Addressing Mistakes and Misconceptions

Another common reason for difficulty is misunderstanding the concept or misapplying a method. If you find yourself stuck, revisit the foundational concepts related to the problem. Are there any assumptions you made that led you down the wrong path? Going back to the basics can often shed light on the problem and help you see where things went wrong.

Review the solution step-by-step: Sometimes retracing your steps allows you to identify where you deviated from the correct method.
Seek alternative methods: If one approach doesn’t work, try to think of different strategies to solve the problem.

By carefully analyzing and understanding the most difficult questions, you can build your skills and confidence in solving even the most complex problems. With practice and persistence, these challenges become stepping stones to greater mastery.

Breaking Down Complex Algebraic Concepts

Some mathematical ideas can seem overwhelming at first glance, especially when they involve intricate relationships or multiple steps. However, by approaching these concepts systematically, you can simplify them and gain a deeper understanding. Breaking down complex topics into smaller, more digestible pieces is an effective way to make sense of challenging material and improve problem-solving skills.

The key to understanding complex topics is to first identify the core elements. By isolating the fundamental components, you can focus on understanding each piece before putting them together. Often, a seemingly difficult problem is just a combination of simpler concepts that require careful attention.

Step-by-Step Approach to Complex Ideas

When dealing with advanced problems, break them down into clear steps to avoid feeling overwhelmed. Start by understanding the basic operations involved, then move on to how these operations interact with one another in the context of the problem. Don’t hesitate to pause and review foundational concepts if needed–often, a small gap in understanding can lead to confusion later on.

Identify the main operations: Focus on the main actions required, such as addition, subtraction, multiplication, or division, and how they relate to each other.
Analyze the structure: Look for patterns or structures within the problem that might simplify the process.
Break it into manageable steps: Work through the problem incrementally, addressing one part at a time.

Building a Strong Foundation

Complex problems often stem from weak foundational knowledge. If you’re struggling with a challenging problem, take the time to revisit basic concepts. Strengthening your understanding of simpler ideas will naturally support your ability to handle more complicated material.

Review fundamental principles: Go over simpler problems that use the same concepts to reinforce your understanding.
Practice regularly: Consistent practice helps you become more comfortable with complex ideas, making it easier to tackle difficult challenges in the future.

By approaching complex topics in small, manageable chunks and reinforcing your foundational knowledge, you’ll build a stronger understanding that makes tackling difficult problems more intuitive over time.

Improving Your Algebra Test Scores

Achieving higher scores on mathematics assessments requires both strategy and consistent effort. By developing a focused approach to learning and practicing key skills, you can improve your performance and approach challenges with greater confidence. The key is not only understanding the material but also mastering the techniques that help you solve problems efficiently and accurately.

Success on exams comes from a combination of preparation, practice, and effective time management. By honing these aspects, you’ll be able to tackle problems more quickly and reduce the likelihood of making mistakes. Focusing on areas that often cause difficulty and reinforcing your understanding can lead to noticeable improvements.

Effective Study Strategies

Adopting efficient study habits can significantly boost your performance. The following techniques are proven to help you retain information and improve problem-solving skills:

Consistent Practice: Regularly solve problems to build familiarity and reinforce concepts.
Focus on Weak Areas: Spend extra time on topics you find challenging to ensure a balanced understanding.
Use Study Guides: Utilize study materials to get an overview of key concepts and practice different types of problems.
Work with a Partner: Study with a peer to discuss and solve problems together, helping reinforce your understanding.

Time Management During Assessments

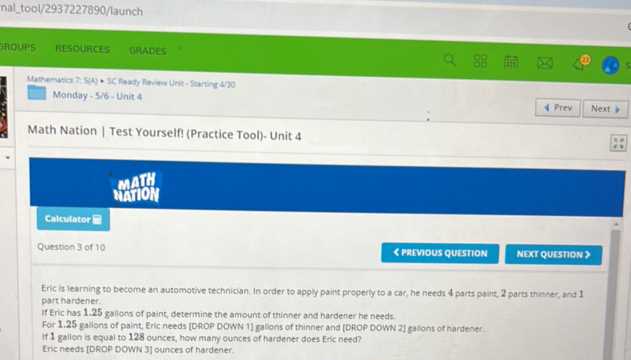
Managing your time effectively during the assessment is crucial. A well-timed approach ensures that you can complete all questions while maintaining accuracy. Here are some tips to maximize your performance during the exam:

Read Questions Carefully: Before diving into solving, make sure you understand each question completely.
Prioritize Easier Questions: Start with questions that you know well to build confidence and save time for more challenging ones.
Allocate Time for Review: If possible, leave time at the end of the exam to review your work for any mistakes or missed details.

By consistently applying these strategies and managing your study time wisely, you’ll increase your chances of success and improve your ability to approach problems with greater confidence.

Using Practice Tests to Your Advantage

Practice assessments are one of the most powerful tools for improving your performance in mathematical problem-solving. They simulate the real exam experience, helping you become more familiar with the format and the types of questions you’ll face. By engaging with these practice problems, you can identify areas where you need improvement and strengthen your skills through repetition.

When used correctly, practice exams can help you develop both confidence and competence. The key is not just to complete them but to analyze your results, understand where mistakes were made, and apply the lessons learned to future problems. Here’s how to maximize the effectiveness of practice tests:

Maximizing the Benefits of Practice Tests

To get the most out of practice exams, follow these strategies:

Replicate Exam Conditions: Simulate the real test environment by timing yourself and working in a distraction-free setting. This helps build focus and time-management skills.
Review Incorrect Answers: After completing the practice test, go back and review the questions you answered incorrectly. Understand why your answer was wrong and what the correct solution method is.
Track Your Progress: Keep a record of your performance on each practice test. This will allow you to see improvements over time and identify patterns in areas that need more focus.
Use Multiple Resources: Take advantage of a variety of practice tests and problem sets. Different resources often offer slightly different questions and approaches, providing a broader range of practice.

Overcoming Challenges with Practice

Sometimes, certain questions or concepts may feel especially challenging. Use these moments as opportunities to strengthen your weaknesses:

Focus on Patterns: Look for recurring themes in the types of questions you struggle with. Understanding these patterns can help you anticipate what may come up in the actual exam.
Break Down Complex Problems: If a question seems overwhelming, break it down into smaller, more manageable parts. Solve each part step by step, and you’ll find that the whole problem becomes easier to tackle.
Seek Clarification: If you’re stuck on a particular concept or problem, ask for help. Whether from a teacher, tutor, or online forum, getting clarification can help you progress faster.

Using practice exams effectively is an ongoing process that can lead to significant improvements. By taking full advantage of these resources, you’ll be better prepared to face any challenge and increase your chances of success.

Exploring Algebraic Techniques for Section 3

Mastering mathematical problems often involves understanding and applying various strategies and methods that can simplify complex tasks. In this section, we’ll explore several techniques that are crucial for solving mathematical expressions and equations effectively. By adopting these methods, you’ll improve your problem-solving skills and become more confident in your ability to tackle challenges.

The key to mastering mathematical techniques lies in breaking down problems into manageable steps and applying the appropriate strategy at the right time. Whether you’re working with linear equations, factoring, or manipulating expressions, each technique has its unique strengths and is suited for different types of problems. Let’s dive into some of the essential methods you’ll encounter.

Key Techniques for Simplifying Equations

One of the most important aspects of solving problems is simplifying equations. Here are some essential techniques to keep in mind:

Factoring: This method involves breaking down expressions into simpler factors. Factoring can help you solve quadratic equations or simplify more complex expressions.
Balancing Both Sides: Ensure that every step you take on one side of an equation is mirrored on the other. This maintains the balance, which is essential for solving equations accurately.
Substitution: This technique involves replacing variables with known values or simpler expressions. It’s especially useful in systems of equations and helps make the problem easier to manage.

Approaching Word Problems with Algebraic Techniques

Word problems can be daunting, but with the right approach, they become much easier to handle. Use the following strategies when working through these problems:

Translate the Problem: The first step in solving a word problem is translating the text into a mathematical equation. Identify key information and variables, then express the relationships between them algebraically.
Define Your Variables: Assign variables to unknowns in the problem. This helps simplify the situation and allows you to work with concrete expressions.
Check Your Work: After solving, always go back to the problem statement to ensure that the solution makes sense in the context of the question. This step is crucial for avoiding mistakes.

By exploring and mastering these algebraic techniques, you’ll be able to approach complex problems with greater ease and confidence. The more you practice these methods, the more proficient you will become at solving mathematical challenges in any form.

How Algebra Nation Prepares You for Exams

Effective preparation for any examination requires a blend of practice, understanding, and strategy. The platform equips students with the tools they need to refine their skills and tackle challenges with confidence. By focusing on key concepts and reinforcing learning through structured activities, it offers a comprehensive approach to mastering the material. As a result, users are well-prepared to handle any problems they may encounter during exams.

The learning environment fosters a deep understanding of mathematical principles while offering ample opportunities for students to apply their knowledge. With various interactive exercises, students are guided through different problem types, enabling them to strengthen their problem-solving abilities. Through consistent practice, users build their confidence and become more adept at navigating complex questions.

Engaging with Practice Problems

One of the most effective ways to prepare is through continuous practice. By working through a wide range of exercises, students are able to:

Reinforce Key Concepts: Repetition helps solidify understanding, ensuring that critical ideas are internalized.
Identify Weak Areas: By tackling different problem types, students can pinpoint areas where they need further improvement.
Build Confidence: The more problems a student solves, the more comfortable they become with the material, reducing test anxiety.

Simulating Real-World Conditions

The platform’s structured activities mimic real exam environments, allowing students to simulate the conditions they’ll face during assessments. This approach encourages students to:

Manage Time Effectively: By practicing under timed conditions, students learn to pace themselves during an exam.
Enhance Focus: Simulating the pressure of a real test environment helps improve concentration and focus.
Apply Problem-Solving Techniques: By using the strategies they’ve learned in practice, students are better prepared to approach unfamiliar problems.

By integrating these techniques into daily study routines, students can improve their performance and enter their exams with confidence, equipped to handle any challenge that arises.

Final Thoughts on Algebra Nation Test Yourself

In conclusion, the platform serves as a valuable resource for students looking to enhance their understanding of key concepts and refine their problem-solving skills. With its interactive features and targeted exercises, it offers a structured approach to learning that can help users boost their confidence and prepare for assessments effectively. Through consistent practice and engagement, users are able to tackle increasingly complex challenges and track their progress over time.

The real benefit of the platform lies in its ability to adapt to individual learning needs. Whether students are reinforcing foundational concepts or advancing to more difficult material, the platform provides a flexible environment to foster growth. This personalized approach ensures that each user can work at their own pace and focus on the areas that require the most attention.

Ultimately, success in any subject comes down to consistent effort, understanding, and strategy. The platform provides an excellent foundation for students to build on, offering the tools and resources needed to improve their skills and achieve their academic goals.