Calculus 1 Final Exam Solutions and Study Guide

Preparing for an important academic evaluation can be a challenging yet rewarding experience. Whether you’re aiming to understand fundamental principles or refine your problem-solving abilities, a structured approach is essential for success. This section is designed to guide you through the essential topics, helping you build confidence and achieve the best possible outcome.

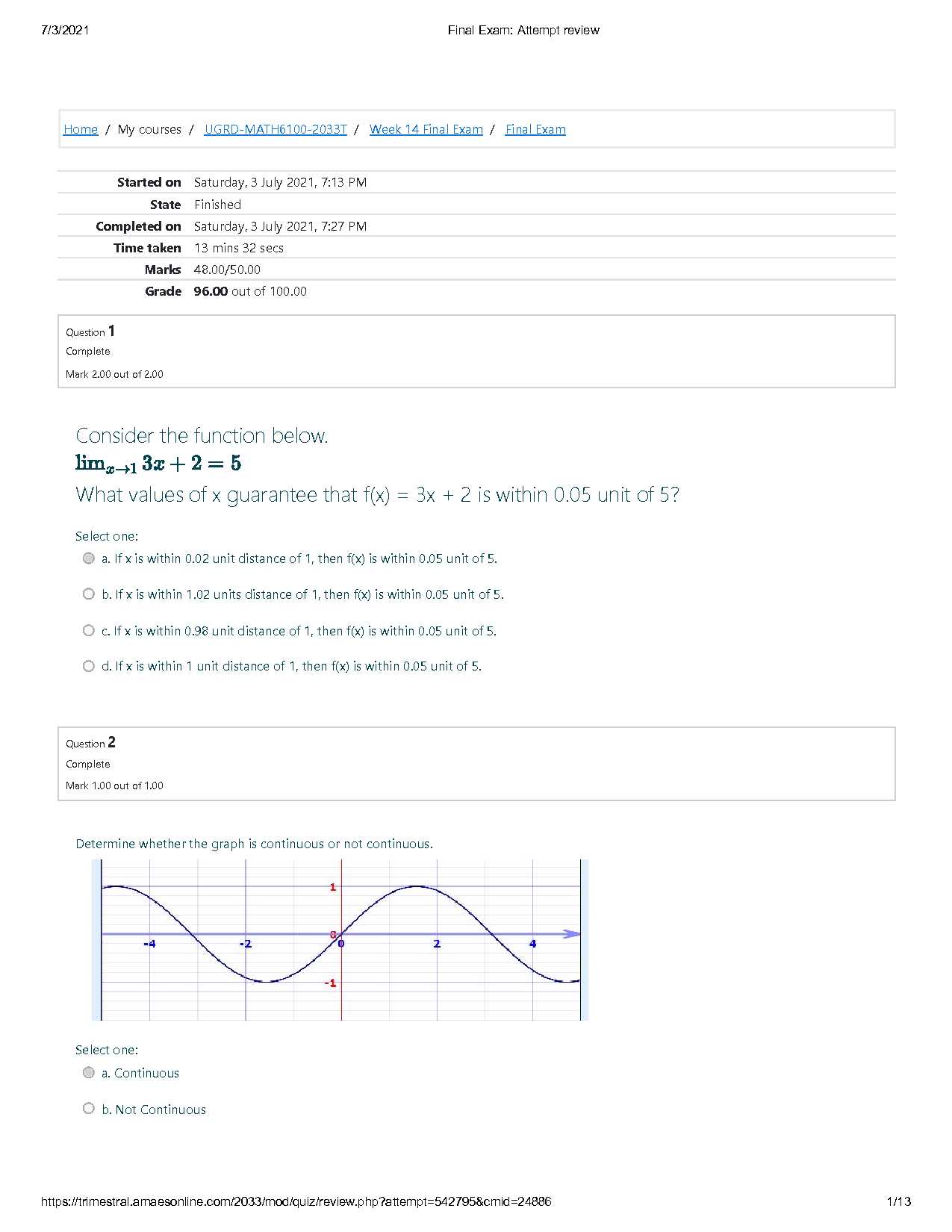
Grasping the core ideas is crucial for tackling complex problems efficiently. By focusing on the most critical areas of study, you can make the preparation process less overwhelming and more manageable. Understanding the underlying theory allows you to approach questions strategically, minimizing errors and maximizing accuracy.

In the following sections, you will find a variety of practice problems and practical insights that will enhance your ability to apply theoretical knowledge in real-world scenarios. With the right preparation, you’ll be ready to face any challenge that comes your way, equipped with the tools and techniques needed to succeed.

Essential Tips for Exam Success

Achieving success in a rigorous assessment requires more than just memorization of formulas and procedures. It involves mastering the key concepts, honing your problem-solving skills, and developing a strategy for tackling various types of questions. By approaching the study process systematically, you can significantly improve your performance and feel more confident when it’s time to take the test.

Focus on Core Concepts

Understanding the foundational principles behind each topic is essential. Instead of simply memorizing steps, aim to understand the reasoning behind the methods. This deeper comprehension will allow you to apply your knowledge to different scenarios, especially when faced with unfamiliar problems. Be sure to revisit the most important topics, such as limits, derivatives, and integrals, and identify how they connect to each other.

Practice Efficient Problem-Solving Techniques

Consistent practice is key to improving your efficiency and accuracy. Work through a variety of problems, focusing not only on the easy ones but also on those that challenge you. The more problems you solve, the better you will become at identifying patterns and quickly applying the appropriate strategies. Don’t shy away from complex questions–these will often be the ones that appear in the test.

Understanding Key Concepts for the Test

To achieve success in any challenging assessment, mastering the essential principles is critical. Instead of focusing solely on individual problems, it’s important to develop a deep understanding of the core ideas that drive the subject. This foundation will not only help you answer the questions correctly but also allow you to adapt to new and complex scenarios.

Here are some of the fundamental concepts you should focus on:

• Limits: Understanding the behavior of functions as they approach specific values is key to solving many problems. This concept forms the basis for differentiation and integration.
• Derivatives: Grasping how to calculate the rate of change and apply this knowledge to real-world problems is essential. Pay attention to the different rules for differentiation.
• Integrals: Understanding the process of finding the area under a curve and its application in various scenarios is another crucial area to focus on.
• Chain Rule: Learn how to combine functions and differentiate them accurately using this technique.

Familiarity with these concepts will give you the flexibility to tackle different types of questions, whether they’re straightforward or more complex. As you practice, try to connect these principles to real-life applications for a better understanding of their importance.

Mastering Limits and Continuity

Understanding the behavior of functions is one of the most important steps in preparing for complex assessments. Two core ideas that form the foundation for many other topics are limits and continuity. Mastering these concepts will not only help you solve problems more efficiently but will also improve your ability to understand how functions behave in various scenarios.

Here’s a breakdown of the key ideas to focus on when studying limits and continuity:

• Limits: Learn how to determine the value a function approaches as the input approaches a specific point. This concept is essential for understanding how functions behave near certain values.
• One-Sided Limits: Understand the difference between left-hand and right-hand limits, which describe the behavior of a function from either direction.
• Continuity: Study how functions behave without breaks or jumps. A function is continuous at a point if it is defined there, the limit exists, and the function’s value equals the limit.
• Indeterminate Forms: Get comfortable recognizing and solving cases where limits produce indeterminate results, such as 0/0 or ∞/∞.

As you prepare, try solving various problems that involve these topics. Practice calculating limits using different techniques, and make sure you understand how to determine whether a function is continuous at a given point. The more you practice, the easier it will become to apply these concepts to more complex problems.

Definite Integrals: Key Insights

Understanding the concept of definite integrals is essential for solving a wide range of problems that involve calculating areas, accumulated quantities, or total change. Unlike indefinite integrals, which provide a general form of the antiderivative, definite integrals yield specific numerical values when evaluated within given bounds. This distinction is key to applying integration in practical contexts such as physics, economics, and engineering.

Here are some important insights to help you grasp this concept:

• Area Under the Curve: A definite integral can be interpreted as the area between a function and the x-axis over a specified interval. This is particularly useful in applications like calculating the total distance traveled or the total accumulated quantity.
• Fundamental Theorem of Calculus: This theorem links differentiation and integration. It states that the definite integral of a function over an interval is equal to the difference between its antiderivative evaluated at the endpoints of the interval.
• Properties of Definite Integrals: Familiarize yourself with important properties, such as linearity (the ability to break down integrals of sums or scalar multiples of functions) and the reversal of limits (changing the bounds of integration changes the sign of the integral).
• Evaluation Techniques: Learn various methods for evaluating definite integrals, including substitution, integration by parts, and numerical methods when an explicit antiderivative is hard to find.

By practicing these techniques and understanding the fundamental principles, you will be able to confidently approach and solve problems involving definite integrals, improving both your problem-solving skills and your conceptual understanding of integration.

Exploring Derivatives and Their Uses

Derivatives are powerful tools in mathematics that help us understand how quantities change in relation to one another. By calculating the rate of change, we can gain insight into the behavior of functions, whether for optimization, motion analysis, or curve sketching. This section focuses on the applications of derivatives and how to leverage them in various problem-solving scenarios.

Real-World Applications of Derivatives

Derivatives are widely used in various fields such as physics, economics, and biology. They allow us to model real-world phenomena and solve practical problems. Some of the key applications include:

• Optimization: Finding maximum or minimum values of functions, such as maximizing profit or minimizing cost.
• Motion Analysis: Derivatives help in understanding speed and acceleration by calculating the rate of change of position over time.
• Curve Sketching: Derivatives provide critical information about the behavior of a function, such as increasing or decreasing intervals, concavity, and points of inflection.

Techniques for Finding Derivatives

There are several standard techniques for computing derivatives, which can be applied depending on the form of the function. Here are some commonly used rules:

Technique	Description
Power Rule	For functions of the form f(x) = x^n, the derivative is f'(x) = n * x^(n-1).
Product Rule	For the product of two functions, the derivative is f'(x) = u'(x)v(x) + u(x)v'(x).
Quotient Rule	For the division of two functions, the derivative is f'(x) = (v(x)u'(x) – u(x)v'(x)) / (v(x))^2.
Chain Rule	Used for composite functions, where the derivative is f'(x) = f'(g(x)) * g'(x).

Mastering these techniques is essential for solving complex problems efficiently. By practicing these methods, you will gain a deeper understanding of how derivatives are used to analyze and solve various types of mathematical challenges.

Techniques for Solving Related Rates

Related rates problems involve finding the rate at which one quantity changes with respect to another. These types of problems often appear in real-world situations, such as determining how fast a shadow lengthens as an object moves or how the volume of a balloon changes as air is pumped into it. The key to solving these problems is identifying the relationship between variables and using derivatives to connect their rates of change.

Step-by-Step Approach

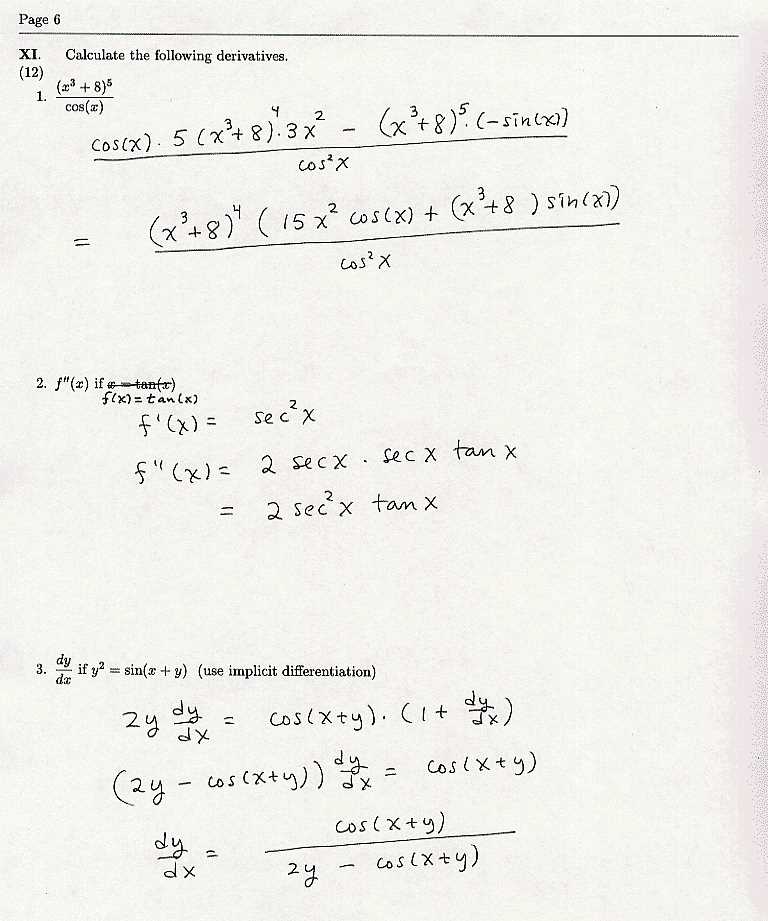
To tackle related rates problems efficiently, follow these essential steps:

1. Identify the variables: Determine which quantities are changing and what you’re asked to find. Assign variables to each quantity and note how they are related.
2. Write an equation: Set up an equation that relates the variables. This equation might involve geometric formulas or physical relationships, depending on the problem.
3. Differentiate with respect to time: Differentiate both sides of the equation implicitly, taking the derivative of each term with respect to time (t). Remember to apply the chain rule when necessary.
4. Solve for the desired rate: After differentiation, solve for the rate you need, substituting known values for other variables. Pay attention to units and ensure that they match appropriately.

Common Types of Problems

Some common scenarios where related rates techniques are used include:

• Volume and surface area changes: Problems involving expanding or shrinking shapes, such as spheres, cones, or cylinders, often ask how their volume or surface area changes with respect to time.
• Motion-related problems: These problems may involve the speed at which an object moves or the rate at which its distance changes over time.
• Shadows and angles: Some problems involve how the length of a shadow changes as an object moves or the rate at which the angle of elevation changes in relation to an object’s height.

By practicing these steps and recognizing patterns in related rates problems, you’ll be able to approach these challenges with confidence and solve them systematically.

Integration By Parts Simplified

One of the most powerful techniques in solving complex integrals is the method of integration by parts. This method is particularly useful when dealing with the product of two functions, allowing you to transform a challenging integral into simpler components. By applying a strategic approach, you can break down the problem into more manageable parts and solve it step-by-step.

Formula and Basic Strategy

The core idea behind integration by parts is based on a formula derived from the product rule for differentiation. The formula is as follows:

∫ u dv = uv – ∫ v du

Here, u and v are functions of the variable of integration. The process involves selecting one function to differentiate (u) and the other to integrate (dv). By choosing wisely, you can simplify the integral considerably.

Step-by-Step Approach

Follow these steps to apply integration by parts effectively:

1. Identify u and dv: Choose a function for u that simplifies when differentiated and a function for dv that is easier to integrate.
2. Differentiate u: Find the derivative of u, denoted as du.
3. Integrate dv: Find the integral of dv, which will give you v.
4. Substitute into the formula: Apply the formula ∫ u dv = uv – ∫ v du to break down the problem into simpler integrals.
5. Solve the resulting integral: The remaining integral ∫ v du should be easier to compute, allowing you to complete the problem.

By practicing this technique, you will become more proficient in recognizing when integration by parts is the most effective method to solve a problem and learn how to apply it quickly and accurately.

Common Mistakes to Avoid in Calculus

When solving mathematical problems, it’s easy to make small errors that can lead to incorrect answers. These mistakes can be particularly frustrating, especially when dealing with complex problems. Recognizing and avoiding common pitfalls is key to mastering the subject and ensuring your solutions are accurate. This section highlights frequent mistakes and provides tips on how to avoid them.

Frequent Errors in Differentiation and Integration

Many students struggle with applying the rules of differentiation and integration correctly. Some of the most common mistakes include:

Type of Mistake	How to Avoid It
Forgetting to apply the chain rule	Always ensure that you differentiate the inner function as well when applying the chain rule.
Misapplying the product or quotient rule	Double-check that you correctly apply each part of the rule, especially when differentiating or integrating products and quotients.
Incorrect limits of integration	When performing definite integration, be careful to correctly identify the upper and lower limits and their corresponding values.
Ignoring constant terms	Ensure you don’t forget to account for constants when integrating or differentiating terms, especially in more complex functions.

Misunderstanding Key Concepts

A strong conceptual foundation is crucial for solving problems efficiently. Some common misunderstandings include:

• Confusing acceleration and velocity: Remember that velocity is the first derivative of position, and acceleration is the second derivative.
• Misinterpreting the Fundamental Theorem: Understand that the theorem connects differentiation and integration, but only under specific conditions.
• Not recognizing implicit differentiation: When dealing with functions of multiple variables, always check for implicit relationships and apply the necessary differentiation rules.

By staying aware of these common mistakes and making a habit of reviewing key principles before solving problems, you can significantly improve your accuracy and efficiency.

How to Tackle Word Problems Effectively

Word problems can often appear overwhelming due to their complex nature and the need to translate real-world scenarios into mathematical expressions. However, breaking down these problems into manageable steps makes them more approachable. By carefully identifying key information and selecting the right approach, you can solve word problems with confidence and accuracy.

Here are some steps to guide you through solving word problems effectively:

1. Read the problem carefully: Take time to understand the scenario. Highlight important data and pay attention to the question being asked.
2. Identify the variables: Determine what quantities are unknown and assign variables to them. This will help you organize your work and establish a relationship between the variables.
3. Translate the words into mathematical expressions: Convert the problem’s verbal statements into equations or formulas that represent the relationships between the quantities.
4. Choose the appropriate method: Based on the type of problem, decide which mathematical technique or formula is best suited to solve it, whether it’s solving an equation, applying a derivative, or using integration.
5. Set up and solve: Set up the necessary equation(s) and carefully solve for the unknown variables. Keep track of units and ensure that each step follows logically from the previous one.
6. Check your answer: After solving the problem, review your work to verify that the answer makes sense in the context of the problem. Check units, signs, and calculations to ensure accuracy.

With practice, you’ll develop a systematic approach to tackling word problems and feel more confident in your ability to solve them efficiently.

Practice Problems for Exam Preparation

One of the most effective ways to prepare for any assessment is through consistent practice. By solving a variety of problems, you can reinforce your understanding of key concepts and develop problem-solving strategies. The more you practice, the more familiar you become with the types of questions that may appear, making you better equipped to handle any challenge that arises.

Types of Problems to Focus On

When preparing, it’s crucial to focus on different problem types to ensure a well-rounded understanding. Here are some categories to consider:

• Basic Derivatives: Practice simple differentiation techniques, such as applying the power rule, product rule, and quotient rule.
• Integration Techniques: Solve integrals using methods like substitution, integration by parts, and handling definite and indefinite integrals.
• Word Problems: Focus on translating real-life situations into mathematical equations, solving them, and interpreting the results.
• Limits and Continuity: Work on problems involving the calculation of limits and understanding continuity in various functions.
• Rate of Change: Practice problems involving rates of change and applying related rate concepts in real-world contexts.

Sample Problems for Practice

Here are a few sample problems to start practicing:

1. Differentiate: Find the derivative of the function f(x) = 3x^2 – 5x + 7.
2. Integrate: Compute the integral ∫(4x^3 – 2x^2 + x) dx.
3. Limit Calculation: Evaluate the limit lim(x → 0) of (sin(x)/x).
4. Word Problem: A ca
   

   Time Management During the Exam

   Effective time management is a critical skill when facing any timed assessment. The ability to allocate your time wisely across different sections ensures that you have ample opportunity to address each problem without feeling rushed. Planning ahead, pacing yourself, and staying focused are essential strategies to maximize your performance under time constraints.

   Prioritize and Plan

   Start by scanning the entire test to get an overview of the questions. Identify which ones are easier or more straightforward, as these can be completed quickly. Allocate more time to complex problems that may require multiple steps or deeper thought. Create a rough time budget based on the number of questions and their difficulty level.

   Stay on Track and Avoid Overthinking

   

   As you work through the problems, stick to your time budget. If you encounter a challenging problem, don’t dwell on it for too long. Move on and come back to it later if time allows. Overthinking can lead to unnecessary stress and wasted time, so trust your preparation and keep moving forward.

   During the assessment, it’s important to regularly check the clock. This ensures that you’re not spending too much time on any one problem and helps you manage your pace throughout the session.

   Reviewing Formulas and Theorems

   

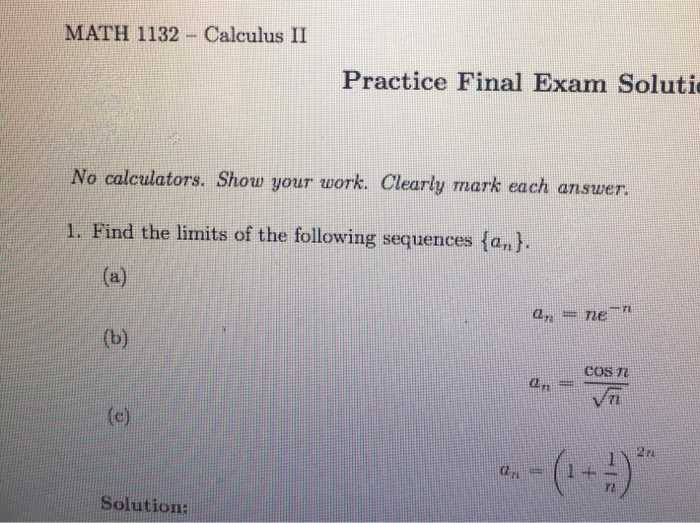
   Reviewing key formulas and theorems is an essential step in preparing for any assessment that requires mathematical problem-solving. By having these principles at the forefront of your mind, you can quickly recognize which tools to apply when faced with different types of problems. Familiarity with the core concepts will help you solve problems more efficiently and reduce the time spent searching for the right method.

   It’s important to understand not just the formulas, but also the conditions under which they apply. For example, certain theorems may be more relevant in specific scenarios, such as using integration rules for particular functions or applying derivative techniques to different types of equations. Revising these concepts will give you the confidence to tackle a wide range of questions during your assessment.

   Here are some of the key areas to focus on when reviewing formulas and theorems:

   • Basic Derivative and Integral Rules: Familiarize yourself with essential formulas like the power rule, product rule, chain rule, and integration by substitution.
   • Limit Theorems: Know how to calculate limits and theorems related to continuity, especially for piecewise functions and rational expressions.
   • Fundamental Theorem of Calculus: This connects derivatives and integrals, allowing you to evaluate integrals using antiderivatives.
   • Area and Volume Formulas: Review methods for finding areas under curves and volumes of solids, such as using definite integrals to compute areas and applying disk or shell methods for volumes.

   By regularly revisiting these formulas and theorems, you’ll be better prepared to identify the appropriate strategy for each problem and solve it efficiently.

   Breaking Down the Fundamental Theorem

   

   The Fundamental Theorem is a cornerstone of many mathematical concepts, connecting two important operations: differentiation and integration. Understanding this principle not only simplifies complex problems but also allows for a deeper grasp of how these two operations are related. Essentially, this theorem provides the foundation for calculating areas, volumes, and rates of change in various scenarios, making it an essential concept for problem-solving.

   At its core, the Fundamental Theorem shows that the process of differentiation and integration are essentially inverse operations. This means that when you integrate a function and then differentiate the result, you return to the original function. Similarly, integrating a function over a specific interval gives you the total accumulation of the function’s values within that range, which can be used to find areas under curves or the total quantity of a changing variable.

   Breaking down the theorem into its two key parts helps to clarify its application:

   • First Part: This part establishes that the integral of a function over a certain interval can be calculated by evaluating its antiderivative at the endpoints. It gives us the connection between the process of finding an area and evaluating the function’s behavior at specific points.
   • Second Part: This part tells us that if a function is continuous on an interval, its integral can be differentiated to recover the original function. It shows the relationship between accumulation and instantaneous change.

   By understanding how the Fundamental Theorem links these two concepts, you’ll be better equipped to solve problems involving both integration and differentiation. This connection is crucial for tackling a wide variety of mathematical tasks effectively.

   Interpreting Graphs in Mathematical Problems

   

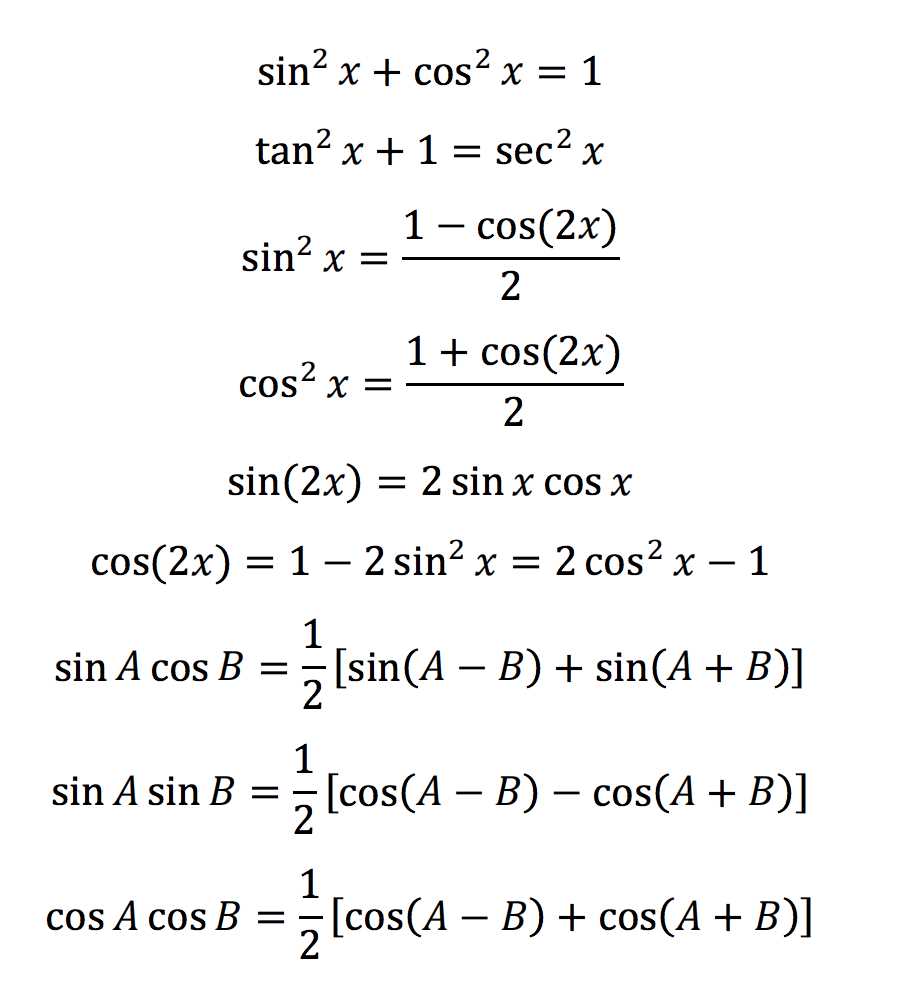
   Graphs are powerful tools in mathematics, providing a visual representation of functions and their behavior. Understanding how to interpret these visualizations is essential for solving problems that involve rates of change, areas under curves, and various other mathematical concepts. By carefully analyzing a graph, you can often identify important properties of a function, such as intervals of increase or decrease, critical points, and asymptotic behavior.

   When interpreting graphs in mathematical contexts, it is important to focus on the overall shape of the curve, the location of specific points, and the slopes of the function at various points. These visual cues can provide insights into the function’s behavior and guide your approach to solving the problem at hand. For example, recognizing the steepness of a graph can help you understand the rate of change, while identifying regions where the graph crosses the axis can indicate the values of the function at key points.

   Here are some key aspects to consider when working with graphs:

   • Critical Points: These are points where the function changes direction, which can help identify local maxima, minima, or inflection points.
   • Intervals of Increase and Decrease: By analyzing the slope of the graph, you can determine where the function is rising or falling.
   • Asymptotes: Look for lines that the graph approaches but never touches, which can indicate limits at infinity or undefined behavior at specific points.
   • Area Under the Curve: The area beneath a graph is often calculated using integration, and it can represent accumulated quantities, such as total distance traveled or total volume.

   By focusing on these elements and practicing graph interpretation, you can improve your ability to solve problems involving functions and better understand the underlying mathematical relationships at play.

   Using Calculators Efficiently in Assessments

   

   In many mathematical assessments, calculators can serve as a valuable tool for simplifying complex computations and saving time. However, it’s essential to use them effectively to maximize their benefits. Knowing when and how to use a calculator is crucial, as over-reliance on it can sometimes lead to missed opportunities for understanding the underlying concepts. This section explores strategies for utilizing a calculator efficiently during an assessment.

   Choosing the Right Functionality

   Before you start using a calculator, it’s important to familiarize yourself with its functions. Most calculators have features such as:

   • Graphing Capabilities: Use the graphing function to visualize equations and identify key points, such as intercepts or maxima/minima.
   • Table of Values: This feature can help you quickly evaluate a function at several points, which is especially useful for analyzing trends or estimating limits.
   • Advanced Operations: Many calculators allow you to compute derivatives, integrals, and solve equations numerically, which can be invaluable when dealing with complex problems.

   Tips for Effective Use

   

   Here are some best practices for using a calculator efficiently during a test:

   1. Double-Check Inputs: Always ensure that the values or expressions entered into the calculator are correct. Small mistakes in typing can lead to incorrect results.
   2. Use for Complex Calculations: Save time by using the calculator for tedious arithmetic or difficult integrations and derivatives, but don’t rely on it for basic steps.
   3. Understand the Process: Even when using a calculator, aim to understand the steps and reasoning behind the computations to ensure you grasp the material fully.
   4. Practice beforehand: Familiarize yourself with your calculator’s functions before the assessment, so you’re not wasting time figuring out how to use it during the test.

   By implementing these strategies, you can effectively harness the power of a calculator while still focusing on the problem-solving process and understanding the material. This balanced approach will help you use the tool to enhance your performance without becoming overly dependent on it.

   Building Confidence with Practice Tests

   One of the most effective ways to prepare for any assessment is by taking practice tests. These simulated challenges provide a clear picture of your strengths and weaknesses, helping you focus your efforts on areas that need improvement. By practicing under timed conditions, you can also become more familiar with the format and pressure of the real assessment. The more you practice, the more confident you’ll become in your ability to tackle similar problems during the actual test.

   While practice tests are valuable for understanding the material, they also help develop essential skills such as time management, critical thinking, and problem-solving. By reviewing each practice session and analyzing mistakes, you can refine your approach and enhance your understanding of key concepts. This iterative process ensures that you’re not just memorizing formulas, but also learning how to apply them effectively.

   Strategies for Effective Practice

   Here are some proven strategies for making the most out of your practice tests:

   • Simulate Real Conditions: Try to recreate the conditions of the actual assessment as closely as possible. This includes timing yourself and minimizing distractions, just as you would during the real test.
   • Review Mistakes Thoroughly: After completing a practice test, go over every error in detail. Understanding why you made a mistake will help you avoid similar errors in the future.
   • Focus on Weak Areas: If you notice recurring mistakes or difficulties in certain topics, spend extra time practicing those areas to strengthen your overall understanding.
   • Track Your Progress: Keep a record of your scores and the types of questions you struggle with. Tracking your improvement over time can boost motivation and give you insight into where you still need work.

   Incorporating practice tests into your study routine not only helps you measure your readiness but also builds the confidence necessary to face the actual challenge. Each test offers an opportunity for growth, pushing you closer to mastering the material.