
Mathematical education plays a crucial role in developing problem-solving abilities and logical thinking. As students advance through different levels of study, they encounter a variety of challenges that require careful analysis and step-by-step solutions. Mastering these challenges often requires access to correct solutions and an understanding of how to approach complex exercises effectively.
This section provides a thorough breakdown of key concepts and solutions, offering guidance for students at various stages of their learning journey. By following a structured approach, learners can gain confidence and improve their skills in tackling a wide range of mathematical problems. Whether you are a parent guiding your child or a student seeking to enhance your understanding, this resource is designed to help simplify the learning process.
We will explore the essential methods for solving common problems, share valuable tips, and highlight the most effective strategies for mastering essential concepts. By understanding how to break down problems and applying the right techniques, students will be better prepared to face future challenges with confidence and success.
Saxon Math Course Three Answers

Mastering the essential principles of arithmetic and algebra is crucial for building a strong foundation in higher-level mathematics. A comprehensive understanding of these fundamental concepts equips students with the necessary tools to solve more complex problems. To truly grasp the material, it’s important to have access to the right resources that clarify difficult topics and guide learners through their exercises step by step.
Effective Problem Solving Strategies
Successful completion of exercises requires more than just knowing the right solution. It involves understanding the process behind each step and how to apply logical reasoning to reach the correct result. By focusing on problem-solving techniques, students can build their confidence and improve their ability to approach unfamiliar challenges. Whether it’s understanding equations, fractions, or geometric concepts, having the right approach makes all the difference.
Utilizing Available Resources for Success

To support learning, having access to a structured solution guide is invaluable. These resources not only provide answers but also explain the reasoning behind them. This helps learners connect the dots between theory and practice, reinforcing the material covered in lessons. By reviewing solutions carefully, students can identify where they might have gone wrong and learn how to correct their mistakes, ultimately leading to better retention and comprehension.
Overview of Saxon Math Course Three
This section focuses on a foundational educational program designed to guide students through key mathematical concepts, enhancing both their understanding and skills. The aim is to build a solid base in essential problem-solving techniques and ensure mastery of core principles. The structured approach fosters confidence and prepares students for more advanced topics in later studies.
The program is structured to develop critical thinking and arithmetic skills through a variety of topics, each designed to reinforce the understanding of previous lessons while introducing new concepts. Students engage in exercises that promote both independent learning and the ability to apply mathematical logic in real-world situations.
- Introduction to algebraic expressions and equations
- Understanding geometric shapes and their properties
- Exploring fractions, decimals, and percentages
- Developing problem-solving skills through practical examples
- Mastering the basics of number theory and operations
This approach allows for incremental learning, with each lesson reinforcing the previous one, ensuring students fully grasp concepts before moving on to more complex topics. Through consistent practice and review, students can develop a deep understanding that will serve them well in future mathematical endeavors.
Why Choose Saxon Math for Learning
When it comes to building a strong foundation in mathematics, selecting the right educational program is crucial for long-term success. The most effective programs break down complex concepts into manageable steps, allowing learners to progressively build on their knowledge and skills. A structured approach helps students not only understand the material but also apply it with confidence in various problem-solving scenarios.
This specific program stands out for its emphasis on continuous review, which ensures that students retain what they’ve learned while gradually introducing new concepts. By revisiting topics at regular intervals, it reinforces understanding and helps learners stay engaged throughout their studies. This method helps prevent gaps in knowledge and promotes a deeper, lasting comprehension of core principles.
Another key benefit is the accessibility of the resources, which cater to diverse learning styles. Whether students thrive with written explanations, visual aids, or hands-on exercises, the program offers a variety of tools to suit different needs. The combination of clear explanations, regular practice, and comprehensive solutions makes it an ideal choice for learners at different stages of their educational journey.
How Saxon Math Helps Build Skills

Building strong problem-solving abilities requires a consistent, structured approach that encourages both practice and understanding. A well-designed program allows students to engage with new concepts while reinforcing previous lessons, creating a solid base for future success. Through its step-by-step methodology, this program helps learners develop critical thinking skills and a deep understanding of essential concepts.
The program’s focus on continuous review and incremental learning ensures that students can strengthen their abilities over time. By revisiting topics regularly, it helps prevent knowledge gaps and solidifies comprehension, ensuring a smoother transition to more advanced subjects. Each lesson is designed to build upon the last, creating a progressive learning experience that enhances overall competency.
| Key Skill | Development Strategy | Impact on Learning |
|---|---|---|
| Problem-Solving | Frequent practice of varied exercises | Improved ability to approach and solve complex tasks |
| Logical Thinking | Step-by-step problem breakdown | Stronger reasoning skills in solving problems |
| Understanding Concepts | Clear explanations and consistent review | Deeper comprehension and retention of material |
| Self-Reliance | Independent exercises and self-assessment | Increased confidence and ability to work autonomously |
By consistently applying these strategies, students develop a set of valuable skills that will serve them well in mathematics and other areas of study. The program’s design helps cultivate a strong work ethic and the ability to solve problems efficiently, making it an essential tool for learners aiming to excel in their education.
Key Concepts in Saxon Math Three
In order to build a strong foundation in mathematics, it’s important to understand the fundamental principles that shape more complex topics. A clear grasp of these key concepts is essential for students to advance to higher levels of study with confidence. This program focuses on providing a deep understanding of the most important areas of arithmetic and algebra, ensuring students develop both competence and critical thinking skills.
Among the core topics covered are arithmetic operations, fractions and decimals, basic geometry, and algebraic thinking. Each of these areas is explored through hands-on exercises that encourage active learning and reinforce conceptual understanding. With a focus on practical application, students are guided through each topic step by step to ensure mastery and retention.
For example, understanding fractions involves not only recognizing the relationship between the parts of a whole but also learning how to manipulate and operate with them in equations. Similarly, basic algebra introduces students to solving simple equations and understanding variables, laying the groundwork for more advanced algebraic techniques. By mastering these essential concepts, learners are equipped with the skills they need for future academic success.
Understanding the Structure of the Course

The design of any educational program plays a key role in shaping how well students absorb and retain new information. A well-structured learning path ensures that each topic is introduced at the right time, allowing learners to progressively build their understanding. This particular program is carefully crafted to provide a balance between new concepts and reinforcement of prior knowledge, making the learning process both manageable and effective.
The structure is divided into clear, sequential units, with each lesson carefully building on the last. This approach allows students to master individual topics before moving on to more complex material, ensuring that no foundational knowledge is overlooked. Regular practice exercises and reviews are integrated throughout to keep skills sharp and reinforce learning, giving students the opportunity to revisit material as needed.
Within each unit, students are introduced to a mix of exercises that challenge both their computational and problem-solving abilities. Lessons are structured in a way that promotes active learning, with opportunities for students to apply what they’ve learned through guided practice. This organization helps create a steady rhythm of learning, review, and mastery, which is crucial for long-term retention and success.
Challenges Students Face in Saxon Math

Despite its structured approach and step-by-step learning, students may encounter several obstacles while working through this educational program. These challenges can arise from the complexity of certain topics, difficulty in mastering new concepts, or even simply the pace at which the material is presented. Understanding these difficulties is the first step in overcoming them and achieving success in the subject.
Complexity of New Concepts
One of the most common challenges is the introduction of new concepts that require a deeper understanding of mathematical reasoning. As students progress, they may struggle with more abstract ideas such as algebraic expressions and fraction manipulation. These topics demand careful attention and practice, and can often feel overwhelming without proper guidance. Some students may find it difficult to connect new concepts with previous lessons, which can create confusion and hinder progress.
Consistency in Practice
Another challenge is the need for constant practice and review. The program’s design emphasizes repetition to ensure that students retain information and build a strong foundation. However, this approach can be taxing for learners who prefer to move at a faster pace or who struggle with repetition. Consistency is crucial to mastering each concept, and without it, students may find themselves falling behind or forgetting key lessons.
Answer Key for Saxon Math Course Three
An answer key is an essential resource for students and educators alike, providing a detailed guide to the solutions for the problems presented throughout the curriculum. It not only offers the correct answers but also gives explanations and step-by-step breakdowns, helping learners understand the reasoning behind each solution. Access to a reliable answer key enhances the learning process by enabling students to check their work and identify areas that need improvement.
Importance of an Answer Key
Having an answer key allows students to verify their solutions and better understand the correct approach to solving each problem. When students are unsure about their methods, they can refer to the key to see where they went wrong. This feedback loop is crucial for building confidence and developing a deeper understanding of the material. The answer key serves as a tool for self-assessment and helps reinforce the learning process by highlighting correct methods and common mistakes.
Using the Answer Key Effectively
While an answer key can be a valuable resource, it is important to use it strategically. Students should attempt problems on their own first, then consult the key for validation and clarification. Simply copying answers without understanding the steps involved can hinder learning. By taking the time to review the process used to arrive at each solution, students can strengthen their problem-solving skills and ensure they fully comprehend each concept.
Step-by-Step Solutions for Practice Problems
One of the most effective ways to master any subject is by working through practice problems with clear, step-by-step solutions. This approach not only helps reinforce concepts but also builds problem-solving skills, allowing students to apply their knowledge with confidence. By breaking down each problem into manageable steps, learners can understand the process and logic behind each solution, making it easier to tackle similar problems in the future.
How Step-by-Step Solutions Help
Step-by-step solutions provide clarity and structure, guiding students through the logical progression needed to solve problems. Rather than simply presenting the answer, these solutions highlight each individual step, showing the student how to apply concepts, perform calculations, and arrive at the correct result. This process helps ensure that students understand both the methods used and the reasoning behind them, which is essential for building a strong foundation in the subject.
Applying the Process to New Problems
Once students have reviewed the detailed solutions for a set of practice problems, they can begin applying the same process to new, similar problems. The key is to approach each problem methodically, breaking it down into smaller parts and using the strategies learned. Over time, this repetitive process builds confidence and mastery, making it easier for students to solve increasingly complex problems with greater speed and accuracy.
How to Use Saxon Math Answer Sheets
Answer sheets are a useful tool for students to verify their work, check their calculations, and ensure that they have understood the material. These sheets provide detailed solutions that show not just the final result, but also the steps involved in reaching it. By using answer sheets effectively, students can improve their problem-solving skills and gain a better understanding of the underlying concepts.
To make the most of the answer sheets, students should follow a systematic approach. After attempting the problems, they should compare their solutions to the answers provided, carefully analyzing any differences. This process allows students to identify mistakes, review the methods used, and understand where they went wrong. In addition, the answer sheets can be a useful guide for reviewing key concepts that might need further clarification.
| Step | Action | Benefit |
|---|---|---|
| 1 | Complete the practice problems independently. | Helps develop problem-solving skills and independent thinking. |
| 2 | Check each solution against the answer sheet. | Identifies mistakes and areas for improvement. |
| 3 | Review the steps shown in the answer sheet. | Clarifies the reasoning behind the solution and reinforces concepts. |
| 4 | Attempt similar problems to apply what has been learned. | Strengthens understanding and increases confidence. |
Tips for Efficient Problem Solving

Effective problem-solving requires both strategic thinking and consistent practice. By developing a methodical approach to tackling problems, students can improve their ability to solve even the most challenging tasks with confidence. The key is to break down complex problems into simpler steps and approach each one with a clear plan. In this section, we’ll explore some tips to help streamline the process and increase efficiency.
To solve problems more efficiently, it’s important to understand the problem thoroughly, organize the information, and apply the most appropriate strategy. Time management and attention to detail also play crucial roles in achieving faster and more accurate solutions. The following table outlines some helpful tips to guide the problem-solving process:
| Tip | Description | Benefit |
|---|---|---|
| Understand the Problem | Read the problem carefully and identify key information. | Clarifies the goal and ensures accurate interpretation. |
| Break It Down | Divide the problem into smaller, manageable parts. | Makes complex problems easier to solve step by step. |
| Use Logical Steps | Apply known strategies and methods to solve each part. | Streamlines the process and minimizes errors. |
| Check Your Work | Review the solution and verify each step for accuracy. | Ensures correctness and identifies any mistakes. |
| Practice Regularly | Consistently work on problems to reinforce learning. | Builds confidence and strengthens problem-solving skills. |
Common Mistakes in Problem Solving
In any learning process, making mistakes is an inevitable part of growth. However, recognizing and correcting common errors can significantly improve understanding and performance. Many learners often fall into similar pitfalls when approaching problems, which can hinder their progress. By identifying these mistakes early, students can develop better problem-solving habits and avoid repeating the same errors in the future.
One of the most common mistakes is rushing through the steps without fully understanding the problem or its requirements. This often leads to incorrect assumptions or skipping critical steps in the process. Another frequent issue is neglecting to double-check work, which can result in small errors that compound over time. Additionally, students sometimes misapply formulas or methods due to lack of familiarity or misunderstanding the underlying concepts.
In order to minimize these mistakes, it is important to stay organized, take time to review each step, and practice regularly. The following list highlights some of the most common errors and how to avoid them:
- Skipping Steps: Trying to solve problems too quickly can lead to missing key steps. Always follow each part of the process carefully.
- Overlooking Key Information: Not paying attention to the problem’s details can result in misunderstanding the question. Ensure all relevant data is considered.
- Misapplying Methods: Using incorrect strategies for solving problems can lead to wrong answers. Make sure you understand the method before applying it.
- Not Checking Work: Neglecting to review your answers can allow small mistakes to go unnoticed. Always verify your solution before finalizing it.
- Inconsistent Practice: Infrequent practice can lead to skill gaps. Consistent problem-solving helps reinforce concepts and improves retention.
How to Review Problem-Solving Solutions

Reviewing solutions to practice problems is an essential part of learning, as it helps identify mistakes and reinforce correct strategies. By examining each step carefully, students can develop a deeper understanding of the concepts and improve their problem-solving skills. This process involves checking the work for accuracy, ensuring that all steps were followed properly, and reflecting on the methods used to reach the solution.
The goal of reviewing is not just to find mistakes, but to understand why certain approaches work and others do not. Here are some strategies to effectively review solutions and improve learning outcomes:
1. Check for Calculation Mistakes
One of the most common errors in solving problems is simple arithmetic mistakes. It’s important to go over each calculation carefully to ensure accuracy. This can be done by:
- Rewriting each step to confirm the logic is correct.
- Using a calculator or a different method to verify calculations.
- Cross-checking results with a trusted source or answer guide.
2. Evaluate the Problem-Solving Process
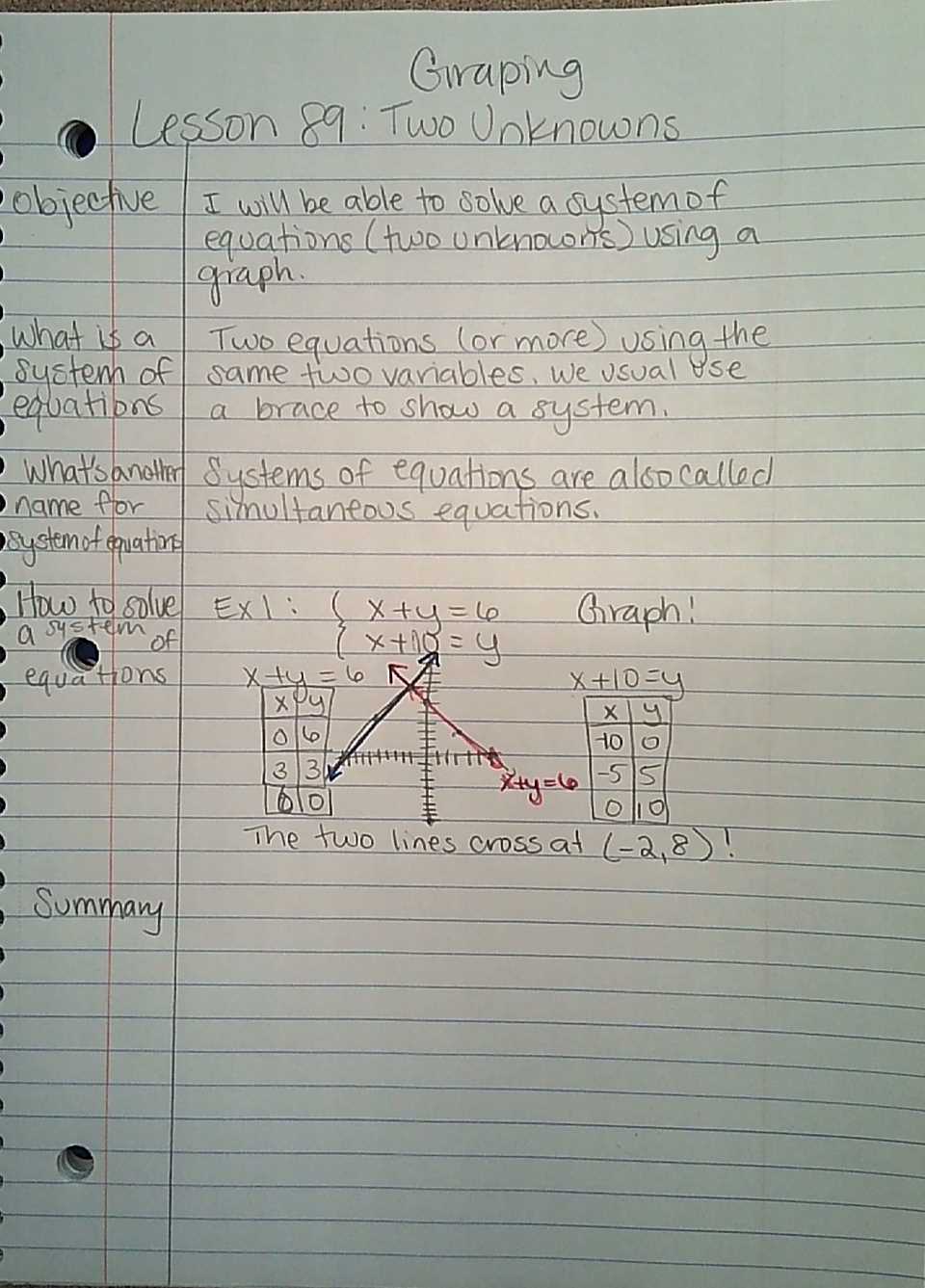
It’s crucial to assess the method used to reach the final answer. Even if the result is correct, the approach may need improvement. Here are some things to look out for:
- Ensure that the correct formula or method was applied for the problem.
- Check if any important information was overlooked.
- Reflect on whether there was a simpler, more efficient approach to the solution.
By using these review strategies, students can not only spot errors but also deepen their understanding and enhance their problem-solving abilities over time. Consistent review is key to mastering the material and building confidence in one’s skills.
Improving Accuracy with Problem-Solving Solutions
Achieving precision in solving practice problems is crucial for mastering any subject. Accuracy ensures that concepts are fully understood and applied correctly. A systematic approach to checking work and refining techniques can help students eliminate common errors, leading to more reliable results and improved skills over time.
To improve accuracy, it’s essential to develop strong habits that support error-free calculations and logical reasoning. Here are some strategies to enhance the accuracy of your work:
1. Break Problems into Smaller Steps
One way to avoid mistakes is by simplifying complex problems. Breaking down each problem into smaller, manageable steps allows for easier tracking and correction along the way. This strategy ensures that no details are overlooked and that all necessary operations are performed correctly. Consider the following tips:
- Identify key information and highlight it before starting the problem.
- Focus on one operation at a time, ensuring each is completed correctly before moving on.
- Write intermediate steps to minimize errors in the final solution.
2. Double-Check Your Work
Verification is a powerful tool in improving accuracy. After completing a problem, take the time to review every step. This extra attention can catch small errors that would otherwise go unnoticed. Here’s how to do it effectively:
- Revisit each calculation to verify all math operations are correct.
- Use an alternative method, such as estimation, to check if your final answer is reasonable.
- Compare your solution with an answer guide or peer to spot discrepancies.
By implementing these strategies, students can reduce the likelihood of errors and increase their overall problem-solving accuracy. Mastery of these skills not only improves performance in practice exercises but also builds confidence in applying these methods to more complex tasks in the future.
Supporting Students with Learning Resources
Effective learning requires more than just instructional material–it also depends on supplementary tools and resources that can help students understand concepts in greater depth. Whether it’s practice problems, guides, or additional explanations, the right resources can make a significant difference in student success. With the right support, learners can overcome challenges and improve their skills efficiently.
Providing access to various learning tools helps students reinforce what they have already learned while offering new ways to approach difficult concepts. Resources can come in various formats, including printed materials, online platforms, or interactive tools. Below are some ways to support students with effective resources:
- Online Tutorials and Videos: Visual learners benefit from tutorials that break down complex concepts into simple steps. Video resources often include demonstrations and examples that clarify difficult topics.
- Practice Sheets: Regular practice is essential for mastering any subject. Printable worksheets with guided exercises help students improve their skills and track progress.
- Interactive Tools: Online platforms with interactive quizzes and games can make learning fun and engaging, offering instant feedback to correct errors in real-time.
- Peer Tutoring: Collaborative learning allows students to discuss problems and solutions with their peers. Group study sessions or one-on-one tutoring can provide personalized support to those who need extra help.
By leveraging these resources, students gain a well-rounded understanding of the subject, build confidence in their abilities, and enhance their learning experience. Providing these tools ensures that every student has the opportunity to succeed at their own pace and in their own way.
Parental Guidance for Effective Learning
Parents play an essential role in a child’s educational journey, particularly when it comes to supporting their learning at home. By providing encouragement, structure, and guidance, parents can help their children build strong foundational skills and overcome challenges in their studies. It’s not only about assisting with homework but also fostering a positive attitude toward learning and cultivating problem-solving strategies.
Here are some practical ways parents can support their child’s learning process:
- Create a Structured Learning Environment: A quiet, well-lit study space free from distractions helps children focus and engage more effectively with their lessons.
- Be Involved in the Process: Stay up to date with what your child is learning and be ready to provide assistance when needed. Ask them about what they’re working on and offer encouragement.
- Promote Consistent Practice: Regular, steady practice leads to better retention and mastery of the subject matter. Help your child set aside time each day for review or practice exercises.
- Encourage Problem-Solving: Instead of giving the answers right away, ask guiding questions that lead your child to think critically and work through problems on their own. This will help them develop important problem-solving skills.
- Provide Positive Reinforcement: Celebrate small victories and improvements to motivate your child to keep going. Positive feedback boosts confidence and encourages a growth mindset.
By actively engaging in their child’s learning, parents help establish a supportive foundation that promotes success. Encouragement, patience, and involvement are key to fostering a lasting love for learning and academic achievement.
Final Thoughts on Effective Learning Strategies

In conclusion, a well-structured educational approach is essential for mastering foundational skills and concepts. By breaking down lessons into manageable sections and emphasizing consistent practice, students are better prepared to understand complex ideas and develop problem-solving abilities. The key to success lies in building confidence, persistence, and a clear understanding of core principles. With the right resources and support, students can thrive and approach challenges with a sense of accomplishment.
Building Confidence Through Consistency

Consistent practice and regular review help students reinforce what they’ve learned and gain a deeper understanding. The process is gradual, but with each small step, confidence grows. The importance of staying persistent, even when the material seems challenging, cannot be overstated. As students continue to apply themselves, their skills improve, creating a solid foundation for more advanced learning.
Support and Encouragement Along the Way
Parents, tutors, and educators all play vital roles in providing the necessary guidance and encouragement. Their involvement helps students stay motivated and focused. Encouragement throughout the learning process–whether through praise for progress or providing helpful feedback–ensures that students remain engaged and confident in their ability to succeed.
Ultimately, the journey of learning is about more than just completing exercises. It’s about developing critical thinking skills, building resilience, and nurturing a love for continuous improvement. With the right mindset and support, students will be well-equipped to face future academic challenges.