Algebra 2 EOC Review Answers and Solutions Guide

Mathematics is a challenging subject that requires both understanding and practice to excel, especially in high school-level assessments. Success in these tests relies on mastering essential concepts and applying them effectively to solve complex problems. Whether you’re preparing for a major exam or aiming to sharpen your skills, knowing how to approach different types of questions is crucial.

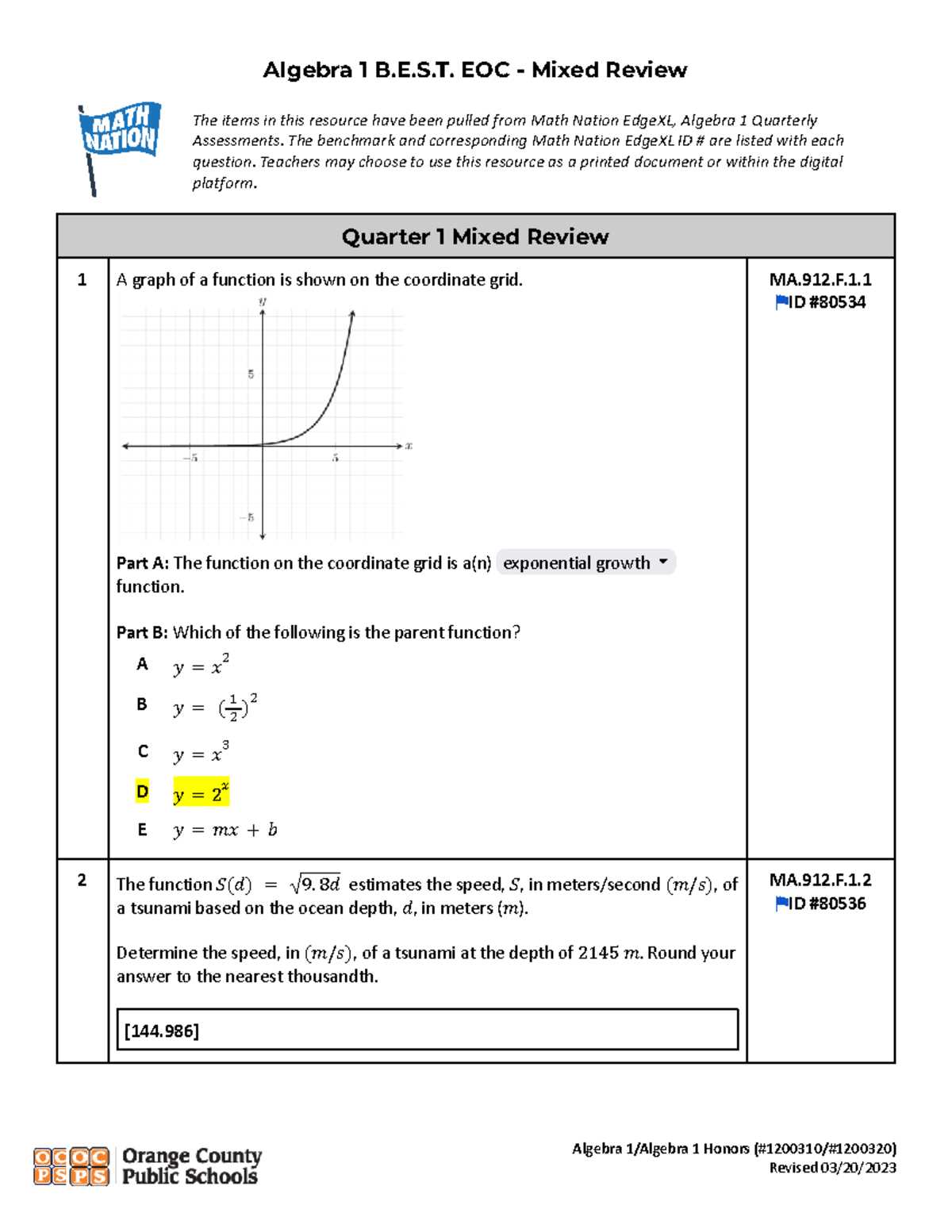
In this section, we will guide you through essential mathematical principles, offering strategies to tackle various problem types. From polynomial equations to graphing techniques, each topic plays a pivotal role in ensuring you’re ready for the most difficult questions. With a structured study plan and focused practice, you’ll build the confidence necessary to perform at your best on exam day.

Strengthening your problem-solving ability through step-by-step explanations and targeted exercises can significantly improve your overall test performance. By understanding the underlying principles, you’ll not only solve equations more efficiently but also develop a deeper appreciation for how different concepts interconnect.

Algebra 2 EOC Review Answers

In order to succeed in advanced mathematical assessments, it is essential to have a strong grasp of key concepts and problem-solving techniques. This section provides a comprehensive approach to the most common problem types, offering clarity and solutions for each. By reviewing critical topics and understanding how to apply the correct methods, you can ensure better performance on your exam.

Focus on mastering the following key areas:

Equations and Inequalities: Learn to solve linear, quadratic, and rational equations, as well as systems of inequalities.
Functions and Graphs: Understand the characteristics and transformations of various types of functions, including quadratic, exponential, and logarithmic.
Polynomials and Factoring: Gain proficiency in factoring complex polynomials and applying different factoring techniques to simplify expressions.
Rational Expressions: Master the process of simplifying, multiplying, dividing, and solving rational expressions and equations.
Exponents and Logarithms: Become skilled at working with exponential and logarithmic functions, solving related equations, and graphing these functions.

To aid your preparation, practice solving problems with step-by-step solutions to enhance your problem-solving speed and accuracy. Pay particular attention to common pitfalls and strategies for avoiding them. By regularly testing yourself and reviewing your mistakes, you’ll improve your ability to recognize patterns and efficiently solve complex problems during the exam.

Finally, make use of online resources, study guides, and practice tests to further reinforce your learning. A structured review plan will not only deepen your understanding but also boost your confidence as you approach your exam date.

Understanding the Exam Format

Before diving into the material, it’s essential to familiarize yourself with the structure of the upcoming test. Knowing how the questions are organized, the time constraints, and the variety of problem types will allow you to approach the exam with greater confidence. By understanding the format, you can tailor your study approach to focus on the areas that will be most heavily tested.

Types of Questions

The assessment typically includes multiple-choice questions, short-answer problems, and long-form questions that require detailed solutions. Multiple-choice questions test your ability to recognize the correct method or result, while short-answer and extended-response questions require you to show your work and reasoning. Preparing for all these question types will ensure you are well-equipped for whatever appears on the test.

Time Management Strategies

Effective time management during the exam is crucial. You will be given a set amount of time to complete all questions, so it’s important to allocate time wisely. Start by answering the easier questions first to gain confidence, then tackle more challenging problems with a focused approach. Practice under timed conditions during your study sessions to get accustomed to the pace required on the actual test.

Key Topics in Algebra 2 Review

Mastering the core topics covered in high-level mathematics is essential for success in any major assessment. These areas are foundational not only for exam preparation but also for applying mathematical principles in real-world scenarios. By focusing on the most crucial subjects, you can build a strong understanding and sharpen your problem-solving skills.

Essential Concepts to Focus On

Below is a list of core topics that you should prioritize during your study sessions. These concepts are commonly tested and form the backbone of many problems on the exam:

Topic	Description	Key Skills
Quadratic Equations	Solving for unknowns in quadratic expressions.	Factoring, completing the square, and the quadratic formula.
Polynomials	Working with expressions involving powers of variables.	Expanding, factoring, and finding roots of polynomials.
Rational Functions	Understanding and simplifying fractions with polynomials in the numerator and denominator.	Simplification, finding asymptotes, and solving equations.
Exponential and Logarithmic Functions	Understanding the relationship between exponential and logarithmic forms.	Solving equations, graphing, and applying properties of exponents and logs.
Systems of Equations	Solving two or more equations simultaneously.	Substitution, elimination, and matrix methods.

Problem-Solving Strategies

Focusing on these topics will allow you to build a comprehensive strategy for tackling complex problems. Develop an understanding of when and how to apply specific methods for each type of equation or function. Regular practice with sample problems will also help reinforce these techniques, allowing you to approach the test with confidence and precision.

How to Approach Algebra 2 Problems

Effectively solving complex mathematical problems requires a structured approach. By breaking down each question into manageable steps, you can identify the most efficient solution methods and avoid common pitfalls. With practice, this methodical approach helps increase both speed and accuracy during exams.

Follow these key strategies when tackling problems:

Step	Action	Tips
Step 1	Read the Problem Carefully	Ensure you understand what is being asked before starting any calculations.
Step 2	Identify the Key Concepts	Determine whether the problem involves equations, graphing, or functions, and select the appropriate method.
Step 3	Set Up the Problem	Translate the given information into an equation or expression that can be solved.
Step 4	Solve Step-by-Step	Perform each operation carefully, ensuring each step logically follows the previous one.
Step 5	Check Your Work	Double-check the solution to ensure accuracy and verify that the solution makes sense in the context of the problem.

Using this approach ensures that you’re not just solving problems but doing so with a clear, organized method. With time, these steps become second nature, improving both your problem-solving speed and reliability under test conditions.

Solving Equations in Algebra 2

Solving equations is one of the foundational skills in mathematics. Mastering the process of finding unknown values requires both understanding different types of equations and knowing which methods to apply to each. Whether you’re working with linear, quadratic, or rational equations, the steps to reach a solution often follow a systematic approach. By practicing various techniques, you can quickly and accurately solve even the most complex problems.

Types of Equations You Will Encounter

There are several key types of equations that you’ll need to solve in advanced math. Each has its own set of rules and strategies:

Linear Equations: These involve variables raised to the first power and can be solved by isolating the variable on one side of the equation.
Quadratic Equations: These involve variables squared and require methods such as factoring, completing the square, or using the quadratic formula to find solutions.
Rational Equations: These involve fractions with polynomials in the numerator and denominator. Solving these often requires clearing denominators and simplifying the resulting equation.
Exponential Equations: These equations have variables in the exponent. Solving these typically involves taking logarithms to simplify the equation.

Strategies for Solving Equations

While each equation type has its own solution method, a few key strategies can be applied across most problems:

Isolate the Variable: For most types of equations, begin by simplifying both sides and isolating the variable. This is especially useful in linear and rational equations.
Check for Special Cases: In quadratic and rational equations, always check for solutions that might not be valid (such as dividing by zero or having negative square roots).
Apply the Right Formula or Method: Whether it’s using the quadratic formula for quadratic equations or applying logarithmic properties for exponential equations, ensure you’re using the correct approach to simplify the equation.

By following these strategies and practicing regularly, you’ll develop a deeper understanding of how to solve a wide variety of equations and improve your performance in assessments.

Mastering Quadratic Functions

Quadratic functions play a crucial role in many mathematical concepts and real-world applications. Understanding how to work with these functions is key to solving a wide range of problems, from simple graphing to more advanced equation solving. By mastering the principles behind quadratics, you will be able to analyze their graphs, find their solutions, and apply these techniques in various contexts.

Key Features of Quadratic Functions

Quadratic functions are typically expressed in the form f(x) = ax² + bx + c, where a, b, and c are constants. Understanding the properties of these functions will help you better understand their behavior. Key aspects to focus on include:

Vertex: The highest or lowest point on the graph, depending on the value of a. The vertex is crucial for graphing the function and finding its maximum or minimum value.
Axis of Symmetry: A vertical line that passes through the vertex and divides the graph into two mirror-image halves.
Roots or Zeros: The x-values where the graph intersects the x-axis. These represent the solutions to the equation and can be found using factoring, the quadratic formula, or completing the square.
Direction of Opening: Determined by the value of a: if a is positive, the parabola opens upwards, and if a is negative, it opens downwards.

Methods for Solving Quadratic Equations

There are several methods available to solve quadratic equations, each suited to different types of problems:

Factoring: If the quadratic can be factored, you can set each factor equal to zero and solve for the variable.
Quadratic Formula: This method, x = (-b ± √(b² – 4ac)) / 2a, works for any quadratic equation and provides solutions even when factoring is difficult.
Completing the Square: This method involves rewriting the quadratic equation so that the left side is a perfect square trinomial, allowing you to solve for the variable.

By understanding these techniques and practicing regularly, you will become proficient in solving and graphing quadratic functions, ensuring that you are well-prepared for any related problems.

Systems of Equations and Inequalities

Solving systems of equations and inequalities involves finding solutions that satisfy multiple conditions simultaneously. Whether you’re dealing with linear equations, nonlinear equations, or inequalities, the goal is to find values for the variables that make all the given expressions true. Mastering these concepts is essential for solving more complex problems in mathematics and its applications.

Systems of equations typically involve two or more equations that must be solved together. There are several methods for solving these systems, each suited to different types of problems:

Substitution Method: Involves solving one equation for one variable and then substituting this expression into the other equation to solve for the remaining variable.
Elimination Method: This method involves adding or subtracting equations to eliminate one variable, allowing you to solve for the other.
Graphical Method: Involves graphing each equation on the same coordinate plane and finding the point of intersection, which represents the solution.

When working with systems of inequalities, the goal is to find the region where the solution sets of the inequalities overlap. This often involves graphing the inequality constraints and determining the feasible region that satisfies all conditions. For linear inequalities, the solution is typically a shaded region on a graph, while for nonlinear inequalities, the region may be more complex.

Both systems of equations and inequalities require strong problem-solving skills and an understanding of how different equations relate to each other. With practice, you will be able to efficiently solve these systems and apply them to real-world problems.

Working with Rational Expressions

Rational expressions involve fractions where the numerator and denominator are polynomials. These expressions are fundamental in many areas of mathematics and can often be simplified, multiplied, divided, added, or subtracted. Understanding how to manipulate and simplify rational expressions is crucial for solving equations that involve fractions and polynomials.

Simplifying Rational Expressions

The first step when working with rational expressions is to simplify them. This can often be done by factoring both the numerator and denominator and canceling out any common factors. Simplifying not only makes the expression easier to work with but also helps identify any restrictions on the variables, such as values that would make the denominator zero.

Factor both the numerator and denominator: Look for common factors that can be canceled out.
Identify restrictions: The values that make the denominator equal to zero are not allowed, so exclude these values from the solution set.

Operations with Rational Expressions

Once simplified, you can perform various operations with rational expressions, similar to operations with simple fractions. When adding or subtracting, ensure that the denominators are the same before combining the numerators. For multiplication and division, multiply or divide the numerators and denominators directly, simplifying the result if possible.

Addition/Subtraction: Find a common denominator, then combine the numerators.
Multiplication: Multiply the numerators and the denominators, then simplify the result.
Division: Multiply by the reciprocal of the divisor, then simplify.

With practice, manipulating rational expressions becomes straightforward. Keep in mind the importance of simplifying your final answers and checking for restrictions on the variable to avoid undefined solutions.

Exponents and Logarithmic Functions

Exponential and logarithmic functions are closely related and form a vital part of higher mathematics. Exponents represent repeated multiplication, and logarithms are the inverse operations of exponents. Understanding how these functions interact and their properties is essential for solving complex equations and analyzing growth, decay, and many real-world phenomena.

Exponential functions take the form f(x) = a * b^x, where a is a constant and b is the base of the exponential. These functions are used to model scenarios such as population growth, radioactive decay, and compound interest. As the input value increases, the output of an exponential function grows or decays at an accelerating rate.

On the other hand, logarithmic functions are the inverse of exponential functions. The general form of a logarithmic function is f(x) = log_b(x), where b is the base, and x is the argument. The logarithmic function answers the question: “To what power must the base b be raised to obtain x?” For example, the logarithm of 1000 with base 10 is 3, because 10^3 = 1000.

Properties of Exponents

When working with exponents, there are several key rules to keep in mind:

Product Rule: a^m * a^n = a^(m+n)
Quotient Rule: a^m / a^n = a^(m-n)
Power Rule: (a^m)^n = a^(m*n)
Zero Exponent Rule: a^0 = 1, for any nonzero number a
Negative Exponent Rule: a^(-n) = 1 / a^n

Properties of Logarithms

Just as there are rules for exponents, logarithms have their own set of properties:

Product Rule: log_b(x * y) = log_b(x) + log_b(y)
Quotient Rule: log_b(x / y) = log_b(x) – log_b(y)
Power Rule: log_b(x^n) = n * log_b(x)
Change of Base Formula: log_b(x) = log_c(x) / log_c(b), where c is any positive number different from 1

These rules are essential for simplifying expressions and solving equations involving exponents and logarithms. By practicing these properties, you can easily manipulate and solve problems involving exponential and logarithmic functions.

Functions and Graphing Techniques

Understanding functions and their graphical representations is a fundamental concept in mathematics. A function defines a relationship between two sets, typically between an independent variable (often x) and a dependent variable (often y). Graphing these functions allows us to visualize how the output changes as the input varies, providing insight into the behavior of the function. Mastery of graphing techniques is essential for solving problems that involve patterns, transformations, and real-world applications.

There are various types of functions, including linear, quadratic, exponential, and rational functions, each of which has its own unique graphical characteristics. The shape of the graph depends on the type of function and its coefficients. By understanding the properties of these functions, such as their domain, range, intercepts, and symmetry, we can accurately sketch their graphs and analyze their behavior.

Key Graphing Techniques

To effectively graph a function, there are several essential techniques to follow:

Identify Key Points: Start by identifying critical points, such as intercepts and vertices. These points provide a basic understanding of the function’s graph.
Understand Transformations: Functions can undergo transformations such as translations, reflections, stretches, and compressions. Recognizing how these affect the graph helps in drawing accurate representations. For example, shifting a graph horizontally or vertically affects the function’s output without changing its shape.
Use Symmetry: Many functions, such as parabolas and even functions, exhibit symmetry. Recognizing this symmetry can make graphing quicker and more efficient.
Plot Points: For more complex functions, plot a set of points by calculating corresponding values for a range of x-values. Connect these points smoothly to reveal the graph’s shape.

Analyzing Graphs of Different Functions

Each type of function has its own characteristic graph:

Linear Functions: These graphs are straight lines and are defined by the equation y = mx + b, where m is the slope and b is the y-intercept.
Quadratic Functions: These graphs are parabolas that open either upward or downward depending on the coefficient of the squared term. The vertex is the highest or lowest point on the graph.
Exponential Functions: These graphs increase or decrease rapidly and are characterized by a constant base raised to a variable exponent. The graph has a horizontal asymptote that the function approaches but never reaches.
Rational Functions: These functions involve ratios of polynomials and often have vertical and horizontal asymptotes. Their graphs can have discontinuities or undefined points.

By mastering these techniques and understanding the characteristics of different types of functions, you will be able to graph any function and analyze its behavior with confidence.

Polynomial Operations and Factoring

Working with polynomials involves performing various operations such as addition, subtraction, multiplication, and division, as well as factoring them into simpler expressions. Mastery of these skills is essential for solving equations, simplifying expressions, and analyzing the behavior of polynomial functions. Factoring is particularly important as it helps to break down complex polynomials into their component parts, which can reveal valuable information about the roots or solutions of an equation.

Polynomial Operations

Before factoring, it’s important to be able to manipulate polynomials through basic operations. These operations are similar to working with numbers, but they involve variables and exponents. The key operations include:

Addition: Combine like terms, which are terms that have the same variable raised to the same power. For example, 3x² + 5x² = 8x².
Subtraction: Like addition, subtract like terms. Be sure to distribute the negative sign across all terms in the second polynomial. For example, 6x³ – (3x³ + 2x²) = 3x³ – 2x².
Multiplication: Multiply each term in one polynomial by every term in the other polynomial, then combine like terms. For example, (x + 2)(x – 3) = x² – 3x + 2x – 6 = x² – x – 6.
Division: Use long division or synthetic division to divide one polynomial by another. This is particularly useful when dividing by binomials or other polynomials of higher degree.

Factoring Polynomials

Factoring polynomials involves expressing the polynomial as a product of simpler polynomials. This is an essential technique for solving polynomial equations. Common factoring methods include:

Common Factor: Look for the greatest common factor (GCF) in each term of the polynomial and factor it out. For example, 6x² + 9x = 3x(2x + 3).
Factoring by Grouping: Split the polynomial into two groups and factor each group separately. This is useful for four-term polynomials. For example, x² + 5x + 2x + 10 = x(x + 5) + 2(x + 5) = (x + 5)(x + 2).
Difference of Squares: Recognize polynomials of the form a² – b², which can be factored as (a – b)(a + b).
Trinomial Factoring: Factor trinomials of the form ax² + bx + c. Look for two numbers that multiply to ac and add to b.
Quadratic Formula: For quadratics that are difficult to factor, use the quadratic formula x = (-b ± √(b² – 4ac)) / 2a to find the roots.

By practicing these operations and factoring techniques, you will gain the skills necessary to solve polynomial equations and simplify complex expressions efficiently.

Understanding Complex Numbers

Complex numbers extend the concept of real numbers by introducing a new dimension. They are made up of two parts: a real component and an imaginary component. This allows us to solve equations that would otherwise have no real solutions, particularly when dealing with square roots of negative numbers. Understanding complex numbers is essential for a wide range of mathematical applications, from solving polynomial equations to analyzing electrical circuits and waveforms.

Complex numbers are written in the form a + bi, where a is the real part and b is the imaginary part, and i represents the square root of -1. The imaginary unit i has the fundamental property that i² = -1. This property makes complex numbers an invaluable tool for solving problems that involve negative square roots or other non-real solutions.

Operations with Complex Numbers

Just like real numbers, complex numbers can be added, subtracted, multiplied, and divided. However, there are a few additional steps to keep in mind when performing these operations:

Addition/Subtraction: To add or subtract complex numbers, combine their real and imaginary parts separately. For example, (3 + 4i) + (2 + 5i) = (3 + 2) + (4i + 5i) = 5 + 9i.
Multiplication: Multiply complex numbers using the distributive property, then simplify by replacing i² with -1. For example, (3 + 2i)(1 + 4i) = 3(1 + 4i) + 2i(1 + 4i) = 3 + 12i + 2i – 8 = -5 + 14i.
Division: To divide complex numbers, multiply both the numerator and the denominator by the complex conjugate of the denominator. The complex conjugate of a + bi is a – bi. This eliminates the imaginary part in the denominator.

Complex Conjugates

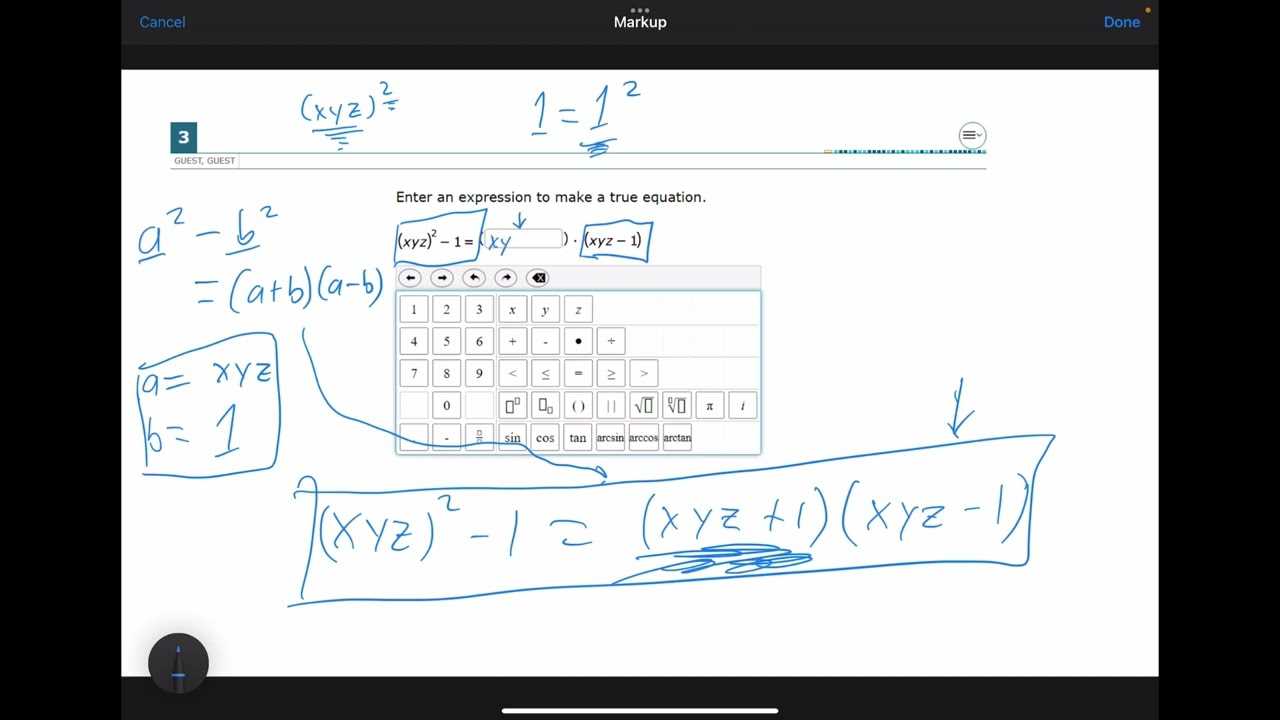
The complex conjugate of a complex number a + bi is a – bi. The conjugate is used when dividing complex numbers or simplifying expressions. When a complex number is multiplied by its conjugate, the result is always a real number:

Example: (3 + 4i)(3 – 4i) = 9 – 16i² = 9 + 16 = 25.

Polar Form of Complex Numbers

Another way to represent complex numbers is in polar form, which expresses a complex number in terms of its magnitude (distance from the origin) and angle (direction) on the complex plane. The polar form of a complex number is written as:

r(cosθ + i sinθ), where r is the magnitude and θ is the angle.

This form is particularly useful in solving equations involving roots of complex numbers and in applications such as electrical engineering.

Complex numbers play a crucial role in expanding the number system and solving problems that involve non-real solutions. With practice, you can become proficient in performing operations with complex numbers and understanding their behavior in various mathematical contexts.

Exponential and Logarithmic Models

Exponential and logarithmic models are powerful tools used to represent and analyze real-world phenomena that grow or decay at rates proportional to their current value. These models are widely applied in various fields, including finance, biology, and physics, to describe processes like population growth, radioactive decay, and compound interest. Understanding these models allows for better predictions and solutions to complex problems that involve rapid changes over time.

Exponential functions describe growth or decay where the rate of change is proportional to the current value. Logarithmic functions, on the other hand, are the inverses of exponential functions, helping to solve equations where the unknown is in the exponent. These two types of functions are closely related and often used together to analyze and solve problems that involve rates of change and scaling effects.

Exponential Functions

An exponential function is typically represented as:

y = ab^x, where a is the initial value, b is the base (rate of growth or decay), and x is the exponent.

Exponential functions can model processes that grow or decay rapidly, such as:

Population Growth: The population of a species can grow exponentially under ideal conditions, where the population doubles at regular intervals.
Radioactive Decay: The amount of a substance decays at a rate proportional to its current amount, modeled by an exponential decay function.
Compound Interest: Investments that compound interest over time can be described using exponential growth, where the money grows at a fixed rate per period.

When solving problems with exponential growth or decay, it’s important to identify the correct values for the initial amount and the rate. In many cases, the natural base e (approximately 2.718) is used to model continuous growth or decay, such as in compound interest or population studies.

Logarithmic Functions

Logarithmic functions are the inverses of exponential functions. The logarithmic form is used to solve for the exponent when the base and result are known. A general logarithmic function is written as:

y = log_b(x), where b is the base, and x is the argument.

Logarithmic functions are used in various applications, including:

Earthquake Magnitude: The Richter scale, which measures earthquake magnitude, is based on logarithmic functions to represent the vast range of energy released by different earthquakes.
pH Level in Chemistry: The pH scale measures the acidity or alkalinity of a solution using a logarithmic scale.
Sound Intensity: The decibel scale for sound intensity is logarithmic, allowing for a manageable representation of sound levels over a large range.

To solve equations involving logarithms, the properties of logarithms–such as the product, quotient, and power rules–are often applied. These properties help simplify complex expressions and make it easier to solve for unknown variables.

By understanding both exponential and logarithmic models, you can gain insights into phenomena that change over time or scale in a non-linear fashion, allowing for more accurate predictions and a deeper understanding of many natural and engineered systems.

Preparing for Word Problems

Word problems often present real-life scenarios that require translating a written description into a mathematical equation. The challenge is to identify the key information, understand the relationships between different elements, and apply the appropriate mathematical techniques to solve the problem. This process involves careful reading, logical reasoning, and sometimes trial and error. Being prepared to tackle these problems requires practice, a solid understanding of mathematical concepts, and a step-by-step approach to breaking down complex situations into manageable parts.

To effectively solve word problems, start by carefully reading the problem and highlighting or underlining the important details. Then, decide on the best strategy, whether it involves setting up an equation, using a formula, or applying a specific mathematical operation. With experience, you can develop a systematic approach that makes solving these problems easier and faster.

Steps to Approach Word Problems

To ensure a logical and organized solution, follow these steps when faced with a word problem:

Read the Problem Carefully: Understand the context and identify the known and unknown quantities. Pay attention to key words like “total,” “difference,” “more than,” or “per” to recognize which operations to use.
Define Variables: Assign variables to the unknown quantities. For example, if the problem asks for the number of apples, let x represent the number of apples.
Set Up an Equation: Translate the relationships described in the problem into an algebraic equation.
Solve the Equation: Use appropriate techniques, such as simplifying expressions, factoring, or applying the quadratic formula, to solve for the unknown variable.
Check the Solution: After solving, check if your solution makes sense in the context of the problem. Verify that the units and conditions of the problem are satisfied.

Common Word Problem Types

There are several types of word problems that you might encounter. Some of the most common include:

Problem Type	Description	Example
Work Problems	Problems where the goal is to determine how long it will take to complete a task or how much work is done in a given amount of time.	Two workers can complete a job in 5 hours and 7 hours, respectively. How long will it take them to complete the job working together?
Mixture Problems	Problems that involve combining different substances, such as liquids or solids, and finding the resulting concentration or quantity.	A chemist mixes two solutions, one with 20% acid and the other with 30% acid. How much of each solution should be mixed to get 100 liters of a 25% acid solution?
Motion Problems	Problems that deal with distance, speed, and time. The relationship between these variables is usually expressed as distance = rate × time.	A car travels 120 miles at a speed of 60 miles per hour. How long does the trip take?
Percent Problems	Problems that involve finding the percentage of a quantity, or determining what percentage one number is of another.	If a store is offering a 15% discount on a jacket priced at $80, how much will the jacket cost after the discount?

By practicing these steps and recognizing the types of word problems you might encounter, you can improve your ability to solve them efficiently. The key is to stay organized, be methodical in your approach, and ensure that every step follows logically from the previous one.

Common Mistakes to Avoid in Algebra 2

As students progress through higher-level mathematical concepts, certain mistakes tend to occur more frequently. These errors can often lead to confusion and incorrect answers, even when the underlying concepts are understood. Recognizing and avoiding common pitfalls is essential for improving problem-solving skills and achieving success. By understanding these mistakes, students can learn to approach problems more carefully, double-check their work, and ensure accuracy in their solutions.

Misunderstanding Operations with Exponents

One of the most frequent mistakes occurs when working with exponents. Many students confuse the rules of exponents, leading to incorrect simplifications. For instance, it’s common to mistakenly apply the addition rule when multiplying terms with exponents of the same base, or to forget to distribute an exponent across a product or quotient.

Incorrect rule application: Remember that (x^a) * (x^b) = x^(a+b), but only when the bases are the same. Misapplying this can lead to errors.
Failure to distribute: When simplifying expressions like (xy)^a, make sure to apply the exponent to both x and y, i.e., (xy)^a = x^a * y^a.

To avoid such mistakes, it’s crucial to regularly practice applying the correct exponent rules and double-check each step for accuracy. This helps solidify understanding and minimizes errors when simplifying or solving problems involving exponents.

Forgetting to Factor or Simplify

Another common mistake is forgetting to factor or simplify expressions properly before solving. In many cases, leaving an expression in an unsimplified or factored form can lead to more complicated steps later in the solution process, or worse, an incorrect result.

Skipping factorization: When working with quadratic equations or polynomials, always check if factoring can simplify the problem before proceeding with more complex methods like the quadratic formula.
Not simplifying fractions: Ensure that fractions are simplified as much as possible to avoid unnecessary complexity, especially when dealing with rational expressions.

Factoring often makes solving equations much easier, so make sure to always look for common factors or patterns, such as difference of squares or perfect square trinomials, before jumping to more complicated techniques.

Sign Errors in Expressions

Sign errors are a common issue when working with negative numbers, especially when distributing or simplifying expressions. It’s easy to make a small mistake when dealing with negative signs, which can lead to a completely incorrect solution. For example, when multiplying two negative numbers, students may incorrectly assume the product is negative, when in fact it is positive.

Distributive errors: Be careful when distributing negative signs across parentheses. For example, -2(x + 3) should be written as -2x – 6, not -2x + 6.
Adding and subtracting negatives: Pay attention when adding or subtracting negative numbers. It’s easy to forget that subtracting a negative number is the same as adding the positive version of that number.

By carefully tracking signs throughout the problem and reviewing each step, it’s possible to reduce the number of errors and make sure that the signs in the final solution are correct.

Recognizing these common mistakes and taking the time to check work at each stage of a problem will not only improve accuracy but also build a deeper understanding of the material. Regular practice, along with a careful and systematic approach, is the key to avoiding errors and mastering these mathematical concepts.

How to Utilize Practice Tests

Practice tests are one of the most effective tools for reinforcing learning and preparing for assessments. They help students identify areas of weakness, become familiar with the format of questions, and build confidence. Rather than simply reviewing materials or memorizing concepts, practice tests provide a real-time simulation of the test-taking experience, allowing students to apply what they’ve learned under timed conditions. The key is to use these tests strategically, reflecting on mistakes and revisiting concepts that need improvement.

When using practice tests, the goal is not just to score well but to learn from the process. Each test should be seen as an opportunity to refine problem-solving techniques, improve time management skills, and gauge overall readiness. After completing a practice test, it is essential to review each question thoroughly, especially the ones answered incorrectly, to understand the reasoning behind the correct solutions.

Steps to Effectively Use Practice Tests

Start Early: Begin using practice tests well before the actual exam. This gives you time to identify areas where you need improvement and allows for multiple attempts to solidify your understanding.
Simulate Test Conditions: Take practice tests in an environment that mimics the real exam as closely as possible. Time yourself and minimize distractions to get a feel for the pressure of the actual test.
Analyze Your Mistakes: After completing the test, carefully review your incorrect answers. Understand why your response was wrong and learn the correct approach for similar problems in the future.
Track Progress: Use practice tests over time to track your improvement. Comparing scores from different sessions will show you how much you’ve learned and where additional focus is needed.
Focus on Weak Areas: Use the insights from practice tests to guide your study sessions. Prioritize concepts or problem types that continue to challenge you, and dedicate additional time to mastering them.

Incorporating practice tests into your study routine will significantly enhance your preparation. By approaching them strategically, you can boost both your understanding of the material and your ability to perform under test conditions.

Time Management for the Exam

Effective time management is crucial for performing well during any high-stakes assessment. Properly allocating your time ensures that you can complete all questions with sufficient attention, reduce stress, and maximize your performance. It’s easy to underestimate how much time each question will take, which can lead to rushing at the end. By using strategic time management techniques, you can ensure that you make the most of your exam time, addressing both easier and more challenging questions effectively.

Before diving into the exam, it’s essential to familiarize yourself with the structure and format of the test. Knowing how many sections there are, how many questions each contains, and the time allocated to the exam will help you pace yourself. The goal is to ensure that no section is left incomplete and that you leave time for reviewing your answers.

Tips for Managing Time During the Exam

Read Instructions Carefully: Before you begin, take a few moments to read the instructions and get an overview of the exam. This can help you plan how to approach each section efficiently.
Allocate Time for Each Section: Break down the total time available and allocate specific minutes for each section. For example, if you have 60 minutes and 3 sections, aim to spend about 20 minutes on each. Adjust as needed based on difficulty.
Prioritize Easy Questions: Start with the questions you find easiest. This will boost your confidence, help you gain momentum, and ensure that you secure those points early on.
Don’t Get Stuck: If you find yourself stuck on a particularly difficult question, move on and come back to it later. Spending too much time on one question can prevent you from completing the rest of the exam.
Use a Timer: Use a watch or the exam’s built-in timer to keep track of time. Setting reminders for when to switch sections or wrap up can help you stay on track.
Reserve Time for Review: Always leave 5-10 minutes at the end to review your answers. This final check can help you spot careless mistakes and make sure you’ve answered everything to the best of your ability.

By practicing good time management strategies during your preparation, you will be more confident in your ability to stay on track and handle time constraints on exam day. The key is to remain calm, focused, and methodical, ensuring that you can answer every question with a clear mind and accurate reasoning.

Resources for Algebra 2 Review

There are a variety of resources available to help you strengthen your understanding and prepare effectively for exams. Utilizing diverse materials such as online tools, textbooks, and study groups can provide a comprehensive approach to mastering key concepts. These resources not only offer practice but also provide explanations, examples, and strategies for tackling complex problems. Leveraging these tools in your study routine can enhance your learning experience and boost confidence for test day.

Whether you’re a visual learner, prefer hands-on practice, or need additional support from instructors, there are options to cater to different learning styles. From interactive websites to traditional study guides, each resource offers unique benefits for reinforcing knowledge and addressing areas of difficulty. It’s important to explore various formats to determine which works best for your personal learning preferences.

Recommended Resources

Online Learning Platforms: Websites like Khan Academy and Coursera offer free lessons, video tutorials, and practice exercises on a wide range of topics.
Interactive Problem Solving: Tools such as Wolfram Alpha and Desmos allow students to visualize equations and functions, making it easier to grasp difficult concepts.
Textbooks and Study Guides: Review books and textbooks are invaluable for understanding theoretical concepts and practicing a variety of problems in depth.
Practice Test Websites: Many websites provide downloadable practice tests and mock exams, offering realistic simulations of the test environment.
Study Groups and Tutoring: Joining a study group or working with a tutor can provide additional support and opportunities for collaborative learning and clarification of difficult concepts.

Using these resources consistently will not only help reinforce your knowledge but will also help you stay organized and focused in the lead-up to the exam. Remember that preparation is key to success, and with the right tools, you can approach the material with confidence and clarity.