As you approach the culmination of your coursework, it’s essential to consolidate your understanding of the key concepts and skills you’ve developed throughout the semester. This section focuses on the critical areas that will help you succeed in your upcoming assessment, covering a range of topics that have been central to your studies. Strengthening your grasp of these concepts will not only help you perform well, but also build a deeper understanding of mathematical principles.
In order to maximize your performance, it’s important to engage with a variety of problem-solving strategies. From solving equations to interpreting complex graphs, each topic offers opportunities to enhance your logical thinking and analytical skills. With thorough preparation, you can approach the test with confidence and demonstrate your full potential.
Key topics will be revisited, and you will be provided with essential tools to tackle any challenge that may arise. Whether you’re refining your techniques or reinforcing foundational ideas, this section will guide you step by step toward a successful outcome. Stay focused and practice consistently for the best results.
Mathematical Concepts Review for Assessment
This section is designed to help you consolidate your knowledge and strengthen your problem-solving abilities as you approach the end of your coursework. By revisiting key topics and practicing essential techniques, you will be better prepared to tackle any challenge. The focus will be on refining your understanding of complex mathematical principles and ensuring you can apply them effectively in various situations.
Key Areas to Focus On
To succeed, you must be familiar with a variety of mathematical concepts and their applications. These range from working with polynomial expressions to understanding the behavior of different types of functions. Below is a breakdown of the most important areas to concentrate on as you prepare for your assessment:
| Topic | Concepts to Review |
|---|---|
| Polynomial Expressions | Factoring, Solving, Graphing |
| Rational Functions | Asymptotes, Simplification, Graph Behavior |
| Systems of Equations | Substitution, Elimination, Graphical Solutions |
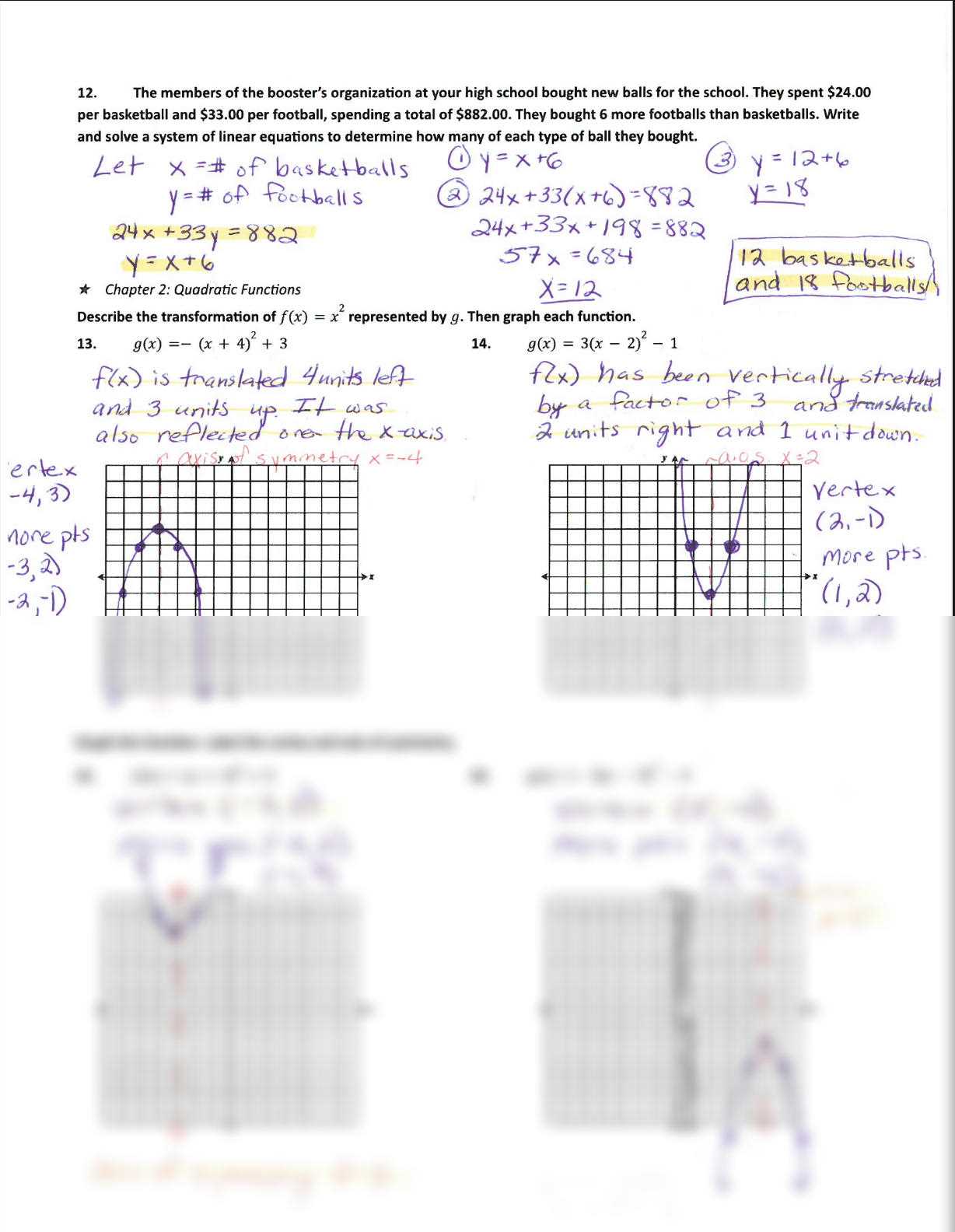
| Exponential and Logarithmic Functions | Solving Equations, Properties, Applications |
| Trigonometry | Unit Circle, Sine and Cosine, Identities |
Problem-Solving Strategies
Effective problem-solving is crucial for mastering mathematical challenges. Focus on developing strategies that help you quickly identify the type of problem and the best method for solving it. Whether you are simplifying expressions or working through word problems, consistent practice and attention to detail will ensure you approach each question with confidence.
Key Topics to Focus On
As you prepare for the upcoming assessment, it is crucial to concentrate on the areas that will most impact your performance. Understanding the core principles of various mathematical concepts will allow you to approach problems with confidence and precision. This section highlights the essential topics that require attention to ensure comprehensive knowledge and problem-solving skills.
Critical Mathematical Concepts
Among the key concepts you should master are functions, equations, and graphing. These topics serve as the foundation for many advanced problems. Gaining a deep understanding of how these elements interconnect will make solving even the most complex questions more straightforward.
| Topic | Concepts to Study |
|---|---|
| Quadratic Equations | Factoring, Completing the Square, Quadratic Formula |
| Rational Expressions | Simplification, Multiplication, Division |
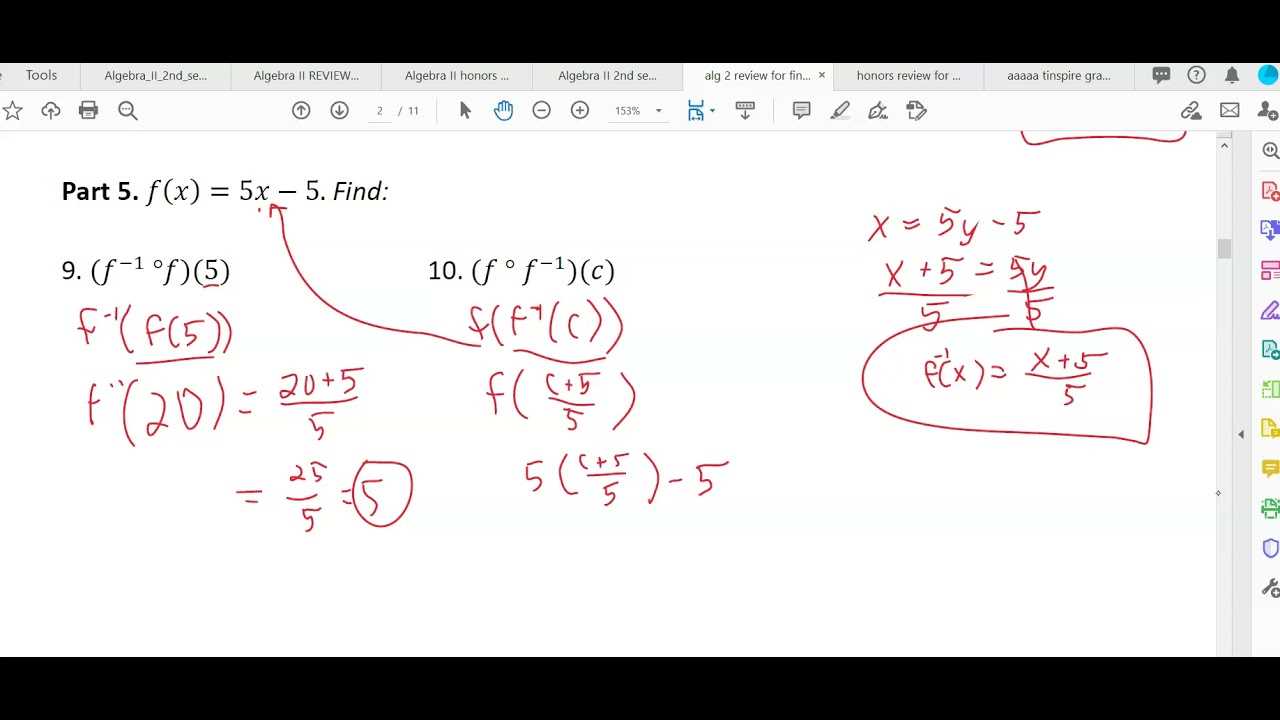
| Functions | Domain, Range, Inverse Functions |
| Systems of Equations | Graphing, Substitution, Elimination Methods |
| Exponents and Radicals | Properties, Simplification, Solving Equations |
Problem-Solving Techniques
Familiarize yourself with different problem-solving strategies to ensure you can tackle various types of questions. Whether working through equations, inequalities, or systems, it’s important to practice these techniques and become comfortable applying them under time constraints.
Understanding Polynomial Functions
Polynomial functions are a critical part of advanced mathematical studies. They form the foundation for solving various types of problems and understanding their behavior is essential. These functions consist of terms that are combined through addition, subtraction, and multiplication, each of which contributes to the overall graph’s shape and properties. To gain a strong understanding, it’s important to explore their structure, how to solve them, and how to graph them effectively.
The general form of a polynomial function is a sum of terms, each with a variable raised to a power, multiplied by a coefficient. As you delve deeper, you will encounter terms such as degree, leading coefficient, and the zeros of the function. Each of these elements provides insight into the function’s behavior and graphical representation.
Key Features of Polynomial Functions
- Degree: The highest exponent of the variable determines the function’s degree, which influences its shape.
- Leading Coefficient: The coefficient of the term with the highest degree affects the direction of the graph.
- Zeros: The points where the polynomial intersects the x-axis are the roots or solutions of the function.
- End Behavior: The function’s behavior as the variable approaches positive or negative infinity is determined by its degree and leading coefficient.
Graphing and Solving Polynomial Equations
Graphing polynomial functions involves understanding their critical points and end behavior. You should practice plotting these functions by identifying the zeros and analyzing how the graph behaves around these points. Additionally, solving polynomial equations can be done by factoring, using the quadratic formula for quadratics, or applying synthetic division for higher-degree polynomials.
- Factoring: Breaking down the polynomial into simpler binomials or trinomials to find solutions.
- Synthetic Division: A streamlined method for dividing polynomials and finding solutions more efficiently.
Mastering Rational Expressions

Rational expressions are a vital component of advanced mathematical problem solving. These expressions involve fractions where both the numerator and denominator are polynomials. Understanding how to manipulate and simplify these fractions is crucial for tackling a wide variety of problems. This section will guide you through the process of simplifying, multiplying, dividing, and solving rational expressions, all while emphasizing key concepts and strategies.
The main challenge when working with rational expressions is understanding how to factor the polynomials involved and how to identify common factors that can simplify the expression. Once you are comfortable with these techniques, you will be able to approach problems more efficiently and accurately.
Essential Operations with Rational Expressions
There are several important operations you will need to master when working with rational expressions:
| Operation | Steps to Perform |
|---|---|
| Simplification | Factor both the numerator and denominator, cancel out common factors, and reduce the expression. |
| Multiplication | Multiply the numerators and denominators, then simplify if possible by canceling out common factors. |
| Division | Multiply by the reciprocal of the divisor, then simplify the resulting expression. |
| Addition/Subtraction | Find a common denominator, rewrite both fractions, then combine the numerators. |
Strategies for Solving Rational Equations
When solving equations that involve rational expressions, the goal is to eliminate the fractions by multiplying both sides of the equation by the least common denominator (LCD). After that, you can solve the resulting polynomial equation. Remember to check for extraneous solutions, as sometimes values that satisfy the simplified equation may not be valid in the original rational expression.
Solving Systems of Equations

When faced with multiple equations involving the same variables, solving systems of equations becomes essential. These systems can represent a variety of real-world situations, such as finding the point where two lines intersect or determining the solution to a set of conditions. There are several methods to solve these systems, and mastering each one will help you approach problems with confidence and accuracy.
Each method–whether through substitution, elimination, or graphing–provides a unique way to find the values of the variables that satisfy all the equations in the system. Understanding when and how to apply each technique is key to solving systems efficiently and correctly.
Methods for Solving Systems
There are three main approaches to solving systems of equations:
- Substitution: Solve one equation for one variable, then substitute that expression into the other equation to find the second variable.
- Elimination: Add or subtract equations to eliminate one variable, allowing you to solve for the other.
- Graphing: Plot both equations on the same graph and identify the point of intersection, which represents the solution.
Tips for Successful Solutions
To solve systems of equations successfully, focus on simplifying the equations as much as possible. Make sure to check your work by substituting the solution back into the original equations to verify that it satisfies both. This step ensures the solution is accurate and consistent with the system.
Exponential and Logarithmic Equations

Exponential and logarithmic equations are fundamental in various mathematical applications, ranging from growth and decay models to complex problem-solving scenarios. These types of equations are interconnected, with one often being used to solve the other. Mastering both forms allows you to manipulate and solve a wide array of problems efficiently. Understanding their properties and how to isolate variables will enable you to approach these problems with confidence.
Exponential equations involve variables in the exponents, while logarithmic equations are the inverse, dealing with the logarithm of a variable. Being able to transform between these two forms is a critical skill in solving these types of equations.
Solving Exponential Equations
To solve an exponential equation, it’s often useful to express both sides of the equation with the same base. Once the bases are equal, you can set the exponents equal to each other and solve for the variable. If the bases cannot be directly matched, logarithms can be used to simplify the equation.
- Example: Solve 3^x = 81 by expressing 81 as a power of 3, so the equation becomes 3^x = 3^4, leading to x = 4.
- Logarithmic Approach: If necessary, apply the natural logarithm (ln) or common logarithm (log) to both sides to bring the exponent down for easier solving.
Solving Logarithmic Equations
Logarithmic equations can be solved by rewriting the equation in exponential form. This allows you to isolate the variable and solve for its value. Sometimes, you may need to apply logarithmic properties such as the power rule, product rule, or quotient rule to simplify the equation first.
- Example: Solve log(x) = 2 by rewriting the equation as 10^2 = x, so x = 100.
- Logarithmic Properties: Use properties like log(a) + log(b) = log(ab) to combine logarithms or split them apart as necessary.
Quadratic Functions and Equations
Quadratic functions and equations are central to understanding the behavior of certain mathematical models. These types of functions are characterized by a squared term and can represent various real-world phenomena, such as projectile motion and profit optimization. A quadratic equation generally takes the form of a polynomial with the highest degree being 2, making it distinct from linear equations.
Solving quadratic equations and graphing their functions requires a firm understanding of key concepts like the vertex, axis of symmetry, and solutions (roots). Mastering these aspects will enable you to approach quadratic-related problems with ease and accuracy.
Key Concepts of Quadratic Functions
- Vertex: The highest or lowest point of the parabola, depending on the direction it opens.
- Axis of Symmetry: A vertical line that divides the parabola into two mirror-image halves, passing through the vertex.
- Roots or Zeros: The points where the quadratic function intersects the x-axis. These are the solutions to the equation when set equal to zero.
- Direction of Opening: Determined by the sign of the leading coefficient. If positive, the parabola opens upward; if negative, it opens downward.
Methods for Solving Quadratic Equations
Quadratic equations can be solved in several ways, each suited to different types of problems. Here are the most common methods:
- Factoring: Express the quadratic equation as a product of two binomials, then solve for the variable.
- Completing the Square: Transform the equation into a perfect square trinomial, then solve for the variable by taking square roots.
- Quadratic Formula: Use the formula x = (-b ± √(b² – 4ac)) / 2a to find the roots, where a, b, and c are the coefficients of the quadratic equation.
Conic Sections Review
Conic sections are the curves formed by the intersection of a plane and a double-napped cone. These shapes are fundamental in geometry and have wide applications in fields such as astronomy, physics, and engineering. Understanding these shapes and their properties is crucial for solving various geometric problems and modeling real-world phenomena.
There are four primary types of conic sections: circles, ellipses, parabolas, and hyperbolas. Each of these shapes has distinct characteristics, equations, and methods for graphing. Knowing how to identify and work with these curves will give you a solid foundation for tackling more advanced topics.
Types of Conic Sections
- Circle: A set of all points equidistant from a fixed center. The equation of a circle is typically written as (x – h)² + (y – k)² = r², where (h, k) is the center and r is the radius.
- Ellipse: A set of points where the sum of the distances from any point on the curve to two fixed points (foci) is constant. Its general equation is (x – h)² / a² + (y – k)² / b² = 1, with a > b for a horizontal major axis and a
- Parabola: A curve that results when the plane intersects the cone parallel to its side. The standard form of a parabola is y = ax² + bx + c for vertical parabolas or x = ay² + by + c for horizontal parabolas.
- Hyperbola: A set of points where the difference in distances from any point on the curve to two fixed points (foci) is constant. Its general equation is (x – h)² / a² – (y – k)² / b² = 1 for horizontal hyperbolas and (y – k)² / a² – (x – h)² / b² = 1 for vertical hyperbolas.
Graphing and Applications
Graphing conic sections involves recognizing the general equation and determining key characteristics such as the center, radius, foci, and axes. The properties of these curves can be applied in various real-world contexts. For instance, ellipses describe planetary orbits, parabolas can model projectile motion, and hyperbolas can represent certain types of radio waves and satellite paths.
Trigonometry Essentials for Algebra
Trigonometry plays a critical role in understanding many concepts in advanced mathematics. Whether it’s solving triangles, analyzing periodic functions, or exploring the relationships between angles and side lengths, mastering trigonometric principles is essential for tackling more complex problems. A solid foundation in this field can significantly enhance your problem-solving abilities in various mathematical contexts.
In this section, we will cover the core concepts and functions that are frequently used in higher-level mathematics. Understanding the basic trigonometric ratios, such as sine, cosine, and tangent, along with their applications, is key to solving many equations and geometric problems. Recognizing how these functions relate to the unit circle and right triangles will also help in visualizing and solving trigonometric equations.
Basic Trigonometric Ratios
- Sine (sin): The ratio of the length of the opposite side to the hypotenuse in a right triangle.
- Cosine (cos): The ratio of the length of the adjacent side to the hypotenuse in a right triangle.
- Tangent (tan): The ratio of the length of the opposite side to the adjacent side in a right triangle.
Applications of Trigonometry
Trigonometric functions are widely used for analyzing periodic behavior such as sound waves, light waves, and seasonal variations. They are also essential for solving real-world problems in engineering, physics, and navigation. In this section, you will learn how to apply trigonometric functions to find missing angles and side lengths in triangles, as well as solve equations involving sine, cosine, and tangent.
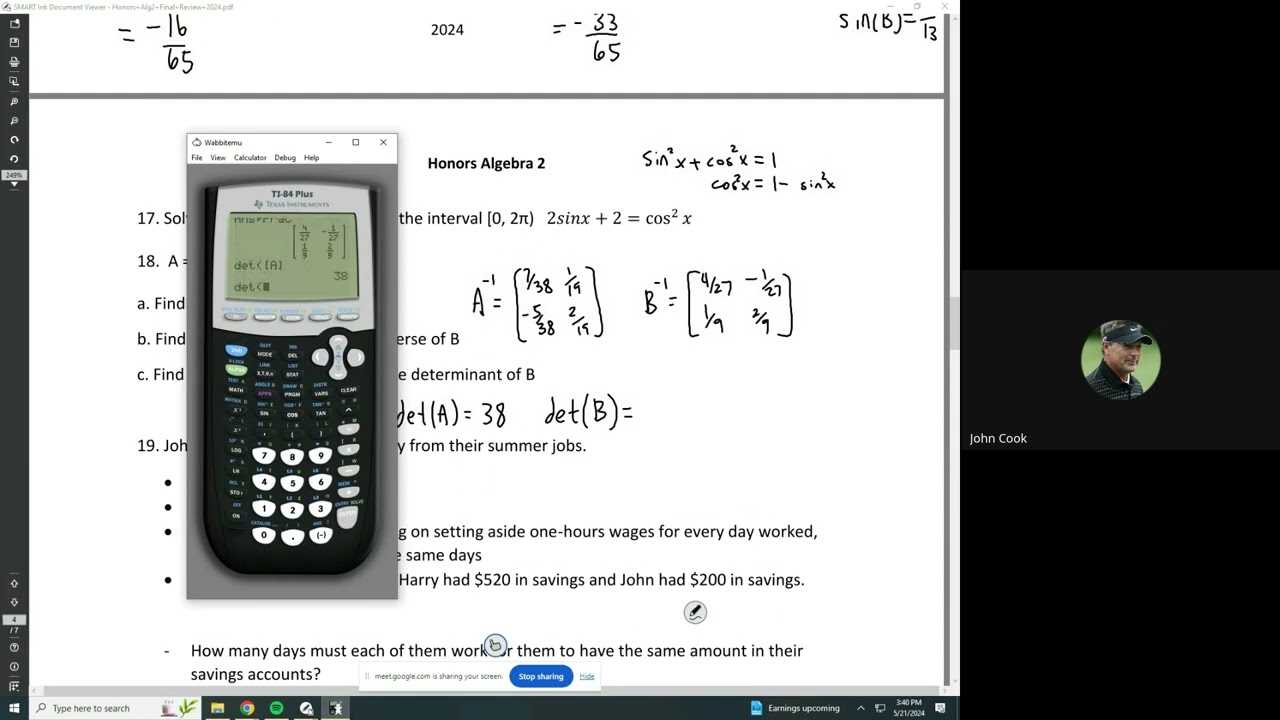
Working with Matrices
Matrices are powerful tools used in various areas of mathematics, especially in systems of equations, transformations, and data manipulation. They allow us to organize and solve complex problems in a more efficient way, often simplifying calculations that would otherwise be difficult to handle manually. Understanding how to perform operations with matrices is essential for solving a variety of mathematical and real-world challenges.
In this section, we will explore the fundamental operations you need to know to work with matrices, including addition, subtraction, multiplication, and finding the inverse. These operations are foundational for solving systems of linear equations, representing transformations, and analyzing data sets.
Basic Matrix Operations

- Matrix Addition: Add corresponding elements from two matrices of the same size to produce a new matrix.
- Matrix Subtraction: Subtract corresponding elements from two matrices of the same size.
- Matrix Multiplication: Multiply rows of the first matrix by columns of the second matrix. Note that the number of columns in the first matrix must equal the number of rows in the second matrix.
Special Types of Matrices
There are several types of matrices that you will frequently encounter, each with unique properties:
- Identity Matrix: A square matrix with ones on the diagonal and zeros elsewhere. It functions like the number 1 in matrix multiplication.
- Zero Matrix: A matrix where all elements are zero.
- Diagonal Matrix: A square matrix where all off-diagonal elements are zero.
By mastering these basic operations and understanding the properties of different types of matrices, you will be well-equipped to handle more complex matrix problems and apply them in various fields such as physics, economics, and computer graphics.
Sequences and Series Explained
Understanding sequences and series is essential for solving problems related to patterns and progressions in mathematics. Sequences represent ordered lists of numbers that follow a specific pattern or rule, while series are the sum of the terms in a sequence. These concepts are used in many fields, including finance, computer science, and engineering, where patterns play a key role in modeling real-world phenomena.
In this section, we will break down the fundamental ideas of sequences and series, explaining the different types, their formulas, and how to work with them effectively. By mastering the formulas for both arithmetic and geometric sequences, as well as learning how to find the sum of a series, you will be able to tackle more complex problems with confidence.
Arithmetic Sequences and Series
An arithmetic sequence is a sequence in which the difference between consecutive terms is constant. The general form of an arithmetic sequence is:
aₙ = a₁ + (n – 1) * d, where aₙ is the nth term, a₁ is the first term, n is the number of terms, and d is the common difference.
The sum of the first n terms in an arithmetic series is given by the formula:
Sₙ = (n / 2) * (a₁ + aₙ), where Sₙ is the sum of the first n terms, a₁ is the first term, and aₙ is the nth term.
Geometric Sequences and Series
A geometric sequence is a sequence in which each term after the first is found by multiplying the previous term by a constant called the common ratio. The general form of a geometric sequence is:
aₙ = a₁ * r^(n – 1), where aₙ is the nth term, a₁ is the first term, r is the common ratio, and n is the number of terms.
The sum of the first n terms in a geometric series is given by the formula:
Sₙ = a₁ * (1 – rⁿ) / (1 – r), where Sₙ is the sum of the first n terms, a₁ is the first term, r is the common ratio, and n is the number of terms. If r is less than 1, this formula simplifies for infinite sums.
| Type of Sequence | General Form | Sum Formula |
|---|---|---|
| Arithmetic Sequence | aₙ = a₁ + (n – 1) * d | Sₙ = (n / 2) * (a₁ + aₙ) |
| Geometric Sequence |
