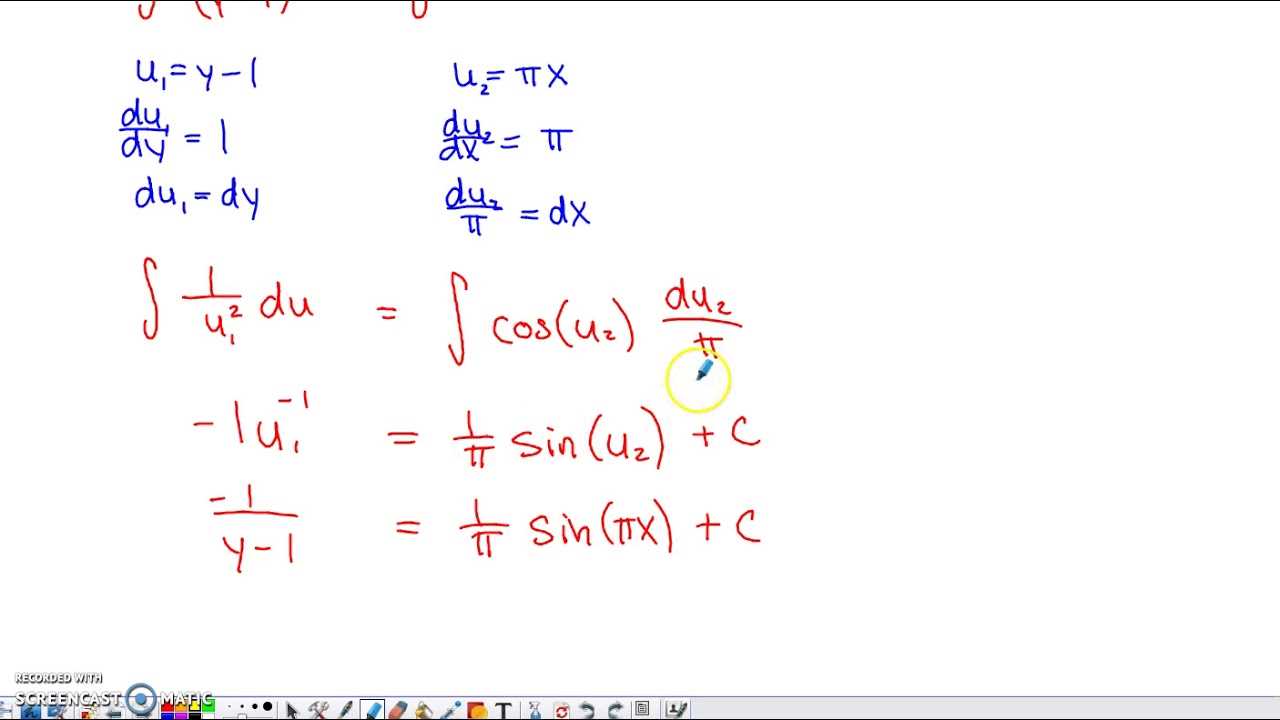
In this section, we explore a series of challenging questions from an important exam, providing in-depth solutions to help you strengthen your understanding of key concepts. By reviewing the problems and their detailed resolutions, you’ll gain insight into the problem-solving process, enhancing your skills for future assessments.
Mastering complex problems requires a clear strategy and an organized approach. Through step-by-step explanations, we break down each task, demonstrating how to identify the essential elements and apply the appropriate techniques. Whether you’re preparing for an exam or aiming to sharpen your knowledge, these detailed solutions offer valuable practice and guidance.
Analyzing these problems will also help you recognize common patterns and mistakes, giving you the tools to avoid them in your own work. By revisiting each challenge, you’ll reinforce your proficiency in various mathematical areas and increase your confidence in tackling similar questions in the future.
2006 AP Exam Problem Solutions Guide
This section covers a set of problems from a key exam, offering detailed solutions to enhance your problem-solving abilities. Each task presents unique challenges designed to test various mathematical skills, and our goal is to provide you with a clear understanding of how to approach and solve them effectively.
By breaking down the questions step by step, you’ll learn the strategies and techniques that can be applied to similar problems. The solutions are not just answers but comprehensive explanations, highlighting important concepts that are essential for mastering the material.
- Problem breakdown: Understand the structure and key elements of each question.
- Solution steps: Follow the logical sequence of actions to reach the correct result.
- Conceptual understanding: Reinforce the underlying principles that drive the mathematical reasoning.
These problems also provide opportunities to practice critical thinking and identify common errors. By reviewing these examples, you’ll be better prepared to face similar challenges with confidence and accuracy. The ability to break down complex problems into manageable parts is a skill that will serve you well in any future mathematical endeavors.
In the following sections, we’ll dive deeper into each question, offering insights into the correct methods and how to apply them in different scenarios. Whether you’re revising for an exam or looking to improve your problem-solving skills, this guide will serve as a valuable resource for your study sessions.
Overview of the 2006 Exam Format
The structure of the exam consists of multiple sections designed to assess a wide range of mathematical and problem-solving skills. Each section challenges the student’s ability to apply concepts in practical scenarios, requiring both analytical thinking and clear communication. Understanding the format is essential for effective preparation, as it allows you to approach each task with confidence and clarity.
The test is typically divided into two main parts: one focused on multiple-choice questions and the other on open-ended problems that require detailed solutions. The second part evaluates your ability to clearly explain your reasoning and work through problems step by step.
| Section | Number of Questions | Time Limit | Weighting |
|---|---|---|---|
| Multiple-choice | 40 | 1 hour | 50% |
| Open-ended | 6 | 1 hour 30 minutes | 50% |
The multiple-choice section is designed to test your knowledge of the key concepts and your ability to identify the correct answers quickly. The open-ended portion is more comprehensive, requiring you to demonstrate how you arrived at your conclusions and to show a deeper understanding of the material. Both sections are important for achieving a high score, and balancing your time between them is crucial for success.
With this format in mind, you can strategically focus on both quick recall and detailed problem-solving, ensuring a well-rounded approach to the exam.
Key Topics Covered in Form B
The exam presents a variety of topics that assess your grasp of mathematical principles and your ability to apply them in different contexts. Understanding the main areas of focus helps you identify where to concentrate your studies and how to approach each problem with the appropriate strategies.
Data analysis is a central theme, requiring you to interpret and manipulate data sets. You may encounter tasks involving measures of central tendency, variability, and probability. Analyzing trends, identifying patterns, and drawing conclusions from raw data are essential skills.
Probability theory is another significant component, where you are tested on your understanding of random variables, distributions, and conditional probability. You will need to calculate probabilities and apply different models to real-world situations.
The exam also delves into the inference and hypothesis testing area, challenging you to make predictions or conclusions based on sample data. Tasks may involve confidence intervals, significance tests, and understanding p-values, which require careful application of the appropriate methods.
Correlation and regression also play a key role, where you will be tasked with identifying relationships between variables and determining the strength and direction of these relationships. Linear models and their interpretations are frequently tested.
Each of these topics is interrelated, and a strong grasp of the underlying concepts will allow you to solve problems efficiently and accurately. By focusing on these areas, you can build the necessary foundation to tackle the more complex challenges in the exam.
Understanding the Grading Criteria
Grading for this exam is based on a combination of accuracy, clarity, and the logical progression of your solutions. The evaluators focus on how well you explain your reasoning, not just the final answers. Properly demonstrating your thought process can earn you partial credit even if the final result is incorrect.
Each task is broken down into specific components that are awarded points based on the correctness and depth of your response. Understanding these criteria can significantly improve your performance, as it allows you to focus on presenting solutions in a clear and structured manner.
| Component | Points Awarded | Focus |
|---|---|---|
| Correctness of Calculation | 2-4 | Accuracy of mathematical operations and results |
| Logical Progression | 2-3 | Clear steps showing how the solution was derived |
| Clarity and Explanation | 1-2 | Well-written reasoning and explanations |
| Use of Proper Formulas | 1-2 | Correct application of relevant equations |
Each question has its own set of expectations, but all are evaluated with the same underlying principles. Clear, concise, and logical solutions are rewarded, while incomplete or poorly explained answers receive fewer points. It’s essential to provide all necessary steps, as skipping or omitting parts of the solution may lead to point deductions.
By understanding these grading criteria, you can ensure that your answers are structured to maximize your score. It’s not just about finding the right answer; it’s about showing the evaluators that you understand the process and can clearly communicate your reasoning.
Common Mistakes in Free Response Questions
When tackling open-ended problems, students often make mistakes that can cost valuable points. These errors usually stem from misunderstandings of the question, misapplication of concepts, or incomplete explanations. Recognizing and addressing these common pitfalls is essential for improving performance in such tasks.
Omitting Necessary Steps
One frequent mistake is skipping critical steps in the solution process. While you may reach the correct answer, failing to show your work can lead to losing points. Even if the final result is right, evaluators need to see the logical progression behind it to fully understand your approach. Always ensure that you include each step, no matter how simple it seems, to demonstrate your method clearly.
Incorrect Interpretation of Data
Another common mistake is misunderstanding the given data or misapplying formulas. This can happen when the question involves multiple pieces of information that need to be combined in specific ways. A simple misinterpretation can lead to a chain of errors, so it’s crucial to carefully read the problem, double-check your assumptions, and apply the correct mathematical techniques.
By being aware of these mistakes, you can take proactive steps to avoid them. Ensure that you show all your work, verify your understanding of the data, and always explain your reasoning to maximize your score.
How to Approach Statistical Problems
When faced with complex problems, having a clear and systematic approach is essential for solving them efficiently. Understanding the question, organizing the information, and applying the right methods are key steps to ensure accuracy. By following a structured process, you can break down even the most challenging tasks into manageable parts.
- Read the problem carefully: Before diving into calculations, ensure you fully understand what the question is asking. Pay attention to the details and what is being measured or compared.
- Identify key data: Extract the important numbers, variables, or categories that are central to the problem. These will be used in your calculations and solutions.
- Choose the right approach: Determine the appropriate method or formula needed. Whether you’re calculating probabilities, analyzing data distributions, or testing hypotheses, the correct technique is crucial for success.
- Break it into steps: Don’t try to solve the entire problem in one go. Break it down into smaller tasks, addressing each part one at a time. This makes the process less overwhelming and ensures accuracy.
- Verify your work: After solving the problem, double-check your calculations and reasoning. Mistakes can easily occur during complex steps, so reviewing your work ensures precision.
By applying these steps to every problem, you can approach each one methodically and with confidence. A clear process helps reduce errors and makes even the most challenging problems more approachable.
Strategies for Efficient Time Management
Effectively managing your time during an exam is crucial for maximizing your performance. With limited hours and a range of tasks to complete, it’s essential to approach each section strategically. Proper planning ensures that you allocate sufficient time to each problem and avoid rushing through critical steps.
Here are a few key strategies to help you stay on track:
| Strategy | Description | Time Allocation |
|---|---|---|
| Prioritize Tasks | Start with problems you find easier or are more confident in. This will help you gain momentum and reduce stress. | 10-15 minutes for simpler questions |
| Time Limits per Question | Set a specific time limit for each question to avoid spending too long on one task. Move on if you’re stuck. | 15-20 minutes per complex question |
| Allocate Time for Review | Leave the last few minutes to review your answers and ensure accuracy. Check for common mistakes. | 10-15 minutes for final review |
By following these time management strategies, you can ensure that you work efficiently, complete all sections of the exam, and leave yourself with enough time to check your work for any potential errors. Prioritizing and allocating time wisely will help you remain calm and focused throughout the test.
Breaking Down the First Free Response Question
The first question in an exam often sets the tone for the rest of the test, providing an opportunity to demonstrate your understanding of key concepts. It typically involves a problem that requires careful analysis and structured reasoning. Approaching this question methodically ensures that you address each part of the problem and maximize your score.
Start by carefully reading the question to understand what is being asked. Identify any important details or specific instructions that will guide your solution. Look for data that needs to be analyzed, relationships between variables, or patterns that need to be recognized. These elements will form the foundation of your response.
Next, break the problem into smaller, manageable parts. Often, the question will have multiple subparts that require different approaches. Tackle each subpart step by step, making sure to show all calculations, logical reasoning, and assumptions. This not only helps you stay organized but also ensures that you don’t miss critical details that could affect your answer.
By following a clear and systematic approach, you can efficiently address the first question and set yourself up for success in the remaining parts of the exam. Don’t rush–take the time to understand each element of the problem and develop a comprehensive solution. This approach will help you earn maximum points while minimizing the risk of errors.
Insights into the Second Free Response Problem
The second problem on the exam often presents a more complex scenario that requires a deeper understanding of concepts. It may involve multiple steps, advanced calculations, or the application of theoretical principles. To succeed in this part of the exam, it’s essential to carefully analyze the question and break it down into its core components.
Start by identifying the primary objective of the question. What is being asked? Are you required to calculate a specific value, interpret a set of data, or make inferences based on the given information? Once you understand the task at hand, outline the steps needed to reach a solution.
Next, organize your approach. If the problem involves data analysis, carefully examine the dataset and determine which methods or formulas are relevant. If the question requires an interpretation of results, ensure you explain your reasoning clearly, backing it up with logical steps and justifications.
By breaking down the problem into manageable parts, you can avoid feeling overwhelmed and ensure a clear, methodical approach. Remember to show all your work and explain your thought process at each stage. This not only demonstrates your understanding but also increases your chances of earning partial credit in case of small errors.
Step-by-Step Solution to Question Three
Question three often involves a multi-step problem that requires both analytical thinking and the application of specific techniques. In this section, we will guide you through each step, providing clear instructions on how to approach and solve the problem effectively. Breaking the problem into smaller parts can help ensure that no detail is overlooked.
Step 1: Understanding the Problem
Start by reading the question carefully. Identify the key information provided and the specific task you need to complete. Look for any data, relationships, or instructions that are critical for solving the problem. This is essential for determining the correct approach.
- Identify what is being asked.
- Highlight important data points or values.
- Note any specific requirements or conditions.
Step 2: Choose the Appropriate Method
Once you have a clear understanding of the problem, decide which method or formula is most suitable for solving it. Whether it involves data analysis, hypothesis testing, or other techniques, the right approach will simplify the problem-solving process.
- Select the relevant formula or approach based on the problem type.
- Apply the formula carefully, ensuring all values are correctly substituted.
- Double-check your approach to ensure it’s the most efficient one for the task.
Step 3: Solve and Verify
Now that you’ve chosen the right method, proceed with the calculations or analysis. Carefully work through each step, showing all intermediate steps and calculations. After completing the solution, verify your work by checking for any potential errors or inconsistencies.
- Perform calculations step by step.
- Check your results against the question’s requirements.
- Ensure all assumptions are clearly stated and justified.
By following these steps, you can approach question three with confidence, ensuring a thorough and accurate solution. Don’t forget to explain your reasoning at each stage to demonstrate your understanding and improve your chances of earning full credit.
Analyzing the Fourth Free Response Task
The fourth task on the exam typically challenges students to apply their understanding of various concepts in a more complex scenario. This problem often involves interpreting data, performing calculations, and making inferences based on the given information. A structured approach is crucial to ensure all aspects of the question are addressed thoroughly.
To begin, carefully read through the problem to understand what is being asked. Take note of the key components and any specific instructions that guide the solution process. Often, such tasks involve multiple parts, each requiring a different skill set or approach. Breaking the problem down into manageable steps will help avoid confusion and ensure you don’t miss important details.
Step 1: Identify the Key Data
In most cases, the problem will provide you with a set of data or a scenario that requires careful analysis. Identify the important pieces of information that you will need to solve the problem, such as numbers, variables, or relationships between different elements.
- Highlight the data points that are central to the problem.
- Look for any trends or patterns in the data.
- Pay attention to any units of measurement or specific instructions.
Step 2: Apply Relevant Techniques
Once you have identified the necessary data, choose the appropriate method or technique for solving the problem. Whether it involves statistical analysis, probability calculations, or other approaches, be sure to apply the method that fits the context of the task.
- Apply the correct formula or algorithm for the task at hand.
- Break the problem into smaller subproblems if needed.
- Ensure each step is clearly explained and justified.
Step 3: Interpret and Conclude
After completing the necessary calculations or analysis, you will likely be asked to interpret your findings and draw conclusions. Take the time to explain your reasoning clearly, referring back to the data and calculations you performed. Provide a concise and well-supported conclusion based on the information given in the task.
- Ensure your conclusion directly addresses the question asked.
- Justify your interpretation with evidence from your work.
- Be sure your response is logical and coherent.
By following these steps, you can effectively analyze and solve the fourth task, demonstrating your ability to apply your knowledge and think critically about the problem at hand. Remember to take your time, show your work, and explain each step clearly to ensure a complete and accurate solution.
Examining the Fifth Free Response Solution
The fifth task on the exam presents a unique challenge, often requiring a combination of analytical skills and problem-solving techniques. This type of problem typically demands a deep understanding of the concepts at hand, along with the ability to apply them in a practical context. To approach this task effectively, it is essential to break it down into smaller components and tackle each one systematically.
When starting this problem, the first step is to carefully read the instructions and identify the key elements that will guide the solution process. Understanding the problem’s context and what is being asked will help you determine the appropriate approach. It’s important to make sure you fully comprehend the underlying question before proceeding with the solution.
Step 1: Identify Key Information
Before you begin the solution, pinpoint the critical data and information that will be necessary for the calculations or analysis. Often, these problems include tables, graphs, or descriptions that are crucial to forming an accurate response.
- Identify important variables and their relationships.
- Look for any conditions or restrictions that may apply to the problem.
- Note any significant patterns or trends that emerge from the data.
Step 2: Select the Appropriate Method
With the key information identified, it’s time to select the appropriate technique or method for solving the problem. The approach will vary depending on the nature of the question, so it’s essential to use the most suitable strategy to address the task effectively.
- Choose the method that aligns with the question’s requirements.
- Ensure all necessary formulas or procedures are applied correctly.
- Take care to show all intermediate steps to make your solution clear.
Step 3: Interpret the Results
Once you’ve completed the calculations or analysis, it’s crucial to interpret the results and answer the question as required. Drawing conclusions from your work and supporting them with the relevant data is essential to demonstrate your understanding and reasoning.
- Explain how the results relate to the problem context.
- Provide a clear and logical conclusion based on your calculations.
- Verify that your interpretation is consistent with the data provided in the problem.
By following these steps, you can effectively approach and solve the fifth task, ensuring a clear, well-structured response. Remember to justify each decision you make, show all work, and explain your reasoning to secure full credit for your solution.
Practice Tips for Answering Free Response Questions
When tackling complex exam questions that require detailed written responses, preparation and practice are key to success. These types of tasks assess not only your knowledge but also your ability to clearly communicate your reasoning and methods. It’s essential to approach each question strategically, break it down into manageable parts, and focus on demonstrating a deep understanding of the concepts involved.
Tip 1: Carefully Read the Question
The first step in addressing any question is to read it thoroughly. Pay close attention to all parts of the prompt and identify what is specifically being asked. Understanding the underlying question is crucial to providing a clear and focused response.
- Highlight or underline important details in the prompt.
- Make sure to note any specific instructions or conditions that must be met.
- Determine whether the problem requires calculations, explanations, or both.
Tip 2: Organize Your Response
Effective organization of your answer can make a significant difference in how well it is received. Present your response in a clear, logical sequence that follows the natural progression of the problem-solving process. This will make it easier for the grader to follow your reasoning and give you full credit for your efforts.
- Start with a brief introduction outlining the steps you plan to take.
- Break the task into smaller, manageable steps and solve them one by one.
- Use bullet points or numbered lists to organize your work when necessary.
- Conclude with a clear summary of your findings or solution.
Tip 3: Show All Work and Justify Your Thinking
One of the most critical aspects of these questions is showing your work. Graders are looking for the process, not just the final result. Make sure to include all intermediate steps, calculations, and explanations that led you to your conclusion.
- Write out all formulas or equations you use, even if they seem obvious.
- Explain your reasoning at each step to demonstrate your understanding.
- Use clear and concise language to ensure that your explanations are easy to follow.
Tip 4: Practice Time Management
Time management is essential when answering tasks that require written responses. Make sure you allocate enough time to each part of the question without rushing through it. Practice under timed conditions to get a sense of how long each section will take, and learn how to pace yourself effectively.
- Set aside a specific amount of time for each part of the problem.
- Don’t spend too long on any one section; move on if you get stuck.
- Reserve time at the end to review and ensure all parts of the question are addressed.
By following these tips and consistently practicing, you can improve your ability to approach these tasks confidently and efficiently. The more you practice, the more familiar you will become with the structure and requirements of such questions, ultimately enhancing both your performance and your understanding of the material.
How to Interpret Complex Statistical Data
Interpreting complex data sets requires a systematic approach to understanding the relationships between different variables and the underlying patterns within the data. It’s important to not only analyze the raw numbers but also to consider their context, meaning, and the conclusions that can be drawn from them. This process often involves breaking down the data into more manageable parts and applying appropriate analytical techniques to extract valuable insights.
Step 1: Identify Key Variables and Relationships
The first step in understanding complex data is identifying the key variables involved and the relationships between them. These variables might represent different aspects of a particular phenomenon or factors that contribute to the outcome you are analyzing. Recognizing which variables are most relevant helps in forming hypotheses and identifying trends.
- Look for independent and dependent variables in the dataset.
- Pay attention to categorical versus continuous data and how they interact.
- Examine the potential correlations or patterns between variables.
Step 2: Visualize the Data
Visualization tools like graphs, histograms, and scatter plots can be invaluable in simplifying complex data. By plotting the data, you can more easily identify trends, outliers, and potential anomalies that might not be as apparent in raw numerical form.
- Use bar charts for categorical data and line graphs for trends over time.
- Scatter plots can help illustrate relationships between two continuous variables.
- Ensure that axes are labeled clearly and scales are consistent.
Once visualized, the data can be analyzed for patterns or inconsistencies that warrant further investigation. For example, are there any clear upward or downward trends? Are there clusters of data points that suggest a specific behavior or relationship? A thorough analysis of the visualized data can offer a clearer path toward meaningful conclusions.
Step 3: Apply Appropriate Analytical Methods

After visualizing the data, applying appropriate statistical techniques helps to validate assumptions and uncover deeper insights. This might include using measures like averages, medians, standard deviations, or more advanced methods like regression analysis or hypothesis testing.
- Calculate measures of central tendency (mean, median) to summarize the data.
- Assess variability using range or standard deviation to understand data spread.
- Consider using correlation or regression models to explore relationships between variables.
By interpreting the data through these lenses, you can better understand how the variables interact and make informed decisions based on the data at hand. The combination of visual tools and statistical methods allows for a comprehensive understanding of complex datasets, leading to more accurate insights and conclusions.
Preparing for Advanced Statistical Topics
As you progress through the study of complex data analysis, preparing for advanced topics requires a solid understanding of the foundational concepts and an ability to apply them in more sophisticated ways. These subjects often involve deeper exploration of data relationships, testing hypotheses, and understanding theoretical models. To succeed in more advanced areas, it’s important to be well-versed in both the theoretical aspects and practical applications of the material.
The first step in preparing for more challenging material is strengthening your grasp of core concepts such as probability, distributions, and sampling methods. These are fundamental to understanding how more complex topics build upon each other. Once these basics are mastered, more advanced topics such as multiple regression, time series analysis, or experimental design will become more approachable.
Another important aspect of preparing for advanced topics is developing the ability to think critically about the data you encounter. This involves not only knowing how to apply certain techniques but also understanding when and why a particular method is appropriate. As you work through problems, focus on honing your analytical skills, such as identifying assumptions, interpreting results, and recognizing potential sources of bias in data.
- Study core concepts in probability and distributions.
- Practice using statistical software for data analysis.
- Work on interpreting complex outputs and drawing meaningful conclusions.
- Engage in exercises that require applying advanced models to real-world data.
Preparation also includes exposure to diverse types of data and methods for analyzing them. This might involve reviewing case studies, engaging in peer discussions, or practicing problem-solving under timed conditions. By actively practicing and applying advanced methods, you’ll gain the confidence needed to tackle more complex statistical challenges in future studies or real-world scenarios.
Utilizing Study Guides for Success
Study guides are invaluable resources when preparing for any exam or assessment, providing a structured way to organize material and focus on key concepts. These guides can help break down complex topics into digestible sections, making it easier to focus on the areas that require the most attention. Whether you are reviewing foundational knowledge or tackling more advanced problems, a well-organized study guide can significantly enhance your preparation and performance.
One of the main advantages of using a study guide is that it can highlight essential topics and concepts that are most likely to appear in exams. It serves as a roadmap, allowing you to prioritize your study time and ensure you cover everything in an efficient manner. By focusing on the most important material, you can avoid feeling overwhelmed and stay on track with your revision.
In addition, study guides often include practice problems and examples that mirror the format and difficulty of the questions you may encounter during your assessment. Working through these exercises allows you to apply your knowledge in a practical setting, strengthening your problem-solving abilities and improving your confidence when faced with similar questions.
To maximize the benefits of a study guide, follow these tips:
- Break the guide into manageable sections and set a schedule to cover each one.
- Take time to understand the explanations behind each concept, not just memorize the content.
- Use practice questions to test your understanding and reinforce key ideas.
- Review any areas where you feel uncertain or confused, seeking clarification as needed.
By incorporating a study guide into your preparation strategy, you are more likely to develop a comprehensive understanding of the material, which is essential for performing well. The guide acts as a focused tool to ensure you are well-prepared and confident when the time for assessment arrives.
Reviewing Common Statistical Formulas
Understanding essential mathematical formulas is critical for solving problems and analyzing data effectively. These formulas provide the foundation for much of the problem-solving work you will encounter, offering a structured way to calculate and interpret different values. Whether working with probabilities, distributions, or data measures, familiarity with key formulas can streamline your approach and ensure accurate results.
Below is a summary of some fundamental formulas that are commonly used in various types of data analysis tasks. Reviewing these will help you become more comfortable with their application and strengthen your problem-solving abilities.
| Formula | Description |
|---|---|
| Mean: ( bar{x} = frac{sum{x_i}}{n} ) | Calculates the average value of a data set by dividing the sum of all values by the number of data points. |
| Variance: ( sigma^2 = frac{sum{(x_i – bar{x})^2}}{n} ) | Measures the spread of data points from the mean, indicating how much variation exists within a data set. |
| Standard Deviation: ( sigma = sqrt{frac{sum{(x_i – bar{x})^2}}{n}} ) | The square root of the variance, providing a more interpretable measure of spread in the same units as the original data. |
| Probability of an Event: ( P(A) = frac{text{Number of favorable outcomes}}{text{Total number of possible outcomes}} ) | Calculates the likelihood of a specific event occurring within a sample space. |
| Confidence Interval: ( bar{x} pm Zleft(frac{sigma}{sqrt{n}}right) ) | Provides a range of values within which the true population parameter is likely to lie, based on sample data and a chosen confidence level. |
| Linear Regression Equation: ( y = mx + b ) | Represents the relationship between two variables, where ( m ) is the slope and ( b ) is the y-intercept. |
By reviewing these formulas and understanding when and how to apply them, you can approach data analysis tasks with greater confidence and accuracy. Whether you’re calculating central tendency measures, analyzing spread, or testing hypotheses, these formulas serve as powerful tools to guide your work.
How to Use Past Exams for Practice
Practicing with previous assessments is one of the most effective ways to prepare for upcoming evaluations. By revisiting past exams, you gain insight into the types of questions that are likely to appear, as well as the level of difficulty you can expect. This method also helps to refine your time management skills and enhances your ability to apply learned concepts in various contexts.
When using older tests for practice, it’s essential to approach them strategically. Begin by familiarizing yourself with the format and types of questions that have been commonly included. Then, attempt to answer each question under timed conditions to simulate the real exam environment. Afterward, review your responses to identify areas where you need further improvement.
Steps for Effective Practice
- Review Past Tests: Start by thoroughly reading through the past exams, noting the structure of each question. Pay attention to recurring themes or topics.
- Time Yourself: Set a timer and practice solving each section within the allotted time to improve your pace.
- Check Solutions: After completing the exam, compare your answers with official solutions, paying particular attention to any errors.
- Identify Weak Areas: Focus on the topics where you made mistakes, and revisit related materials to strengthen your understanding.
- Simulate Exam Conditions: Create mock exams based on multiple years of past tests to enhance your ability to tackle different question types under pressure.
Incorporating this practice into your study routine not only builds familiarity with the exam structure but also helps reinforce key concepts and boosts your confidence. By systematically working through previous tests, you’ll develop a sharper, more analytical approach to solving problems, which is invaluable when it comes to performing well on future evaluations.