
For those preparing for a test in the field of data analysis, a solid understanding of core principles is essential. Mastery of essential techniques and problem-solving methods allows individuals to tackle a variety of challenges with confidence. Practicing with real-world scenarios helps strengthen the ability to interpret, analyze, and communicate results accurately.
Familiarizing yourself with common problem types and approaches to data manipulation can significantly improve performance. As you refine your skills, you will become better equipped to address complex issues, apply mathematical models, and assess outcomes. Effective preparation includes not only theoretical knowledge but also hands-on practice to solidify your understanding.
In this guide, we will explore key strategies, useful examples, and practical tips to help you approach tests in this field. With the right approach, you can confidently navigate through even the most challenging tasks and achieve success in your assessments.
Applied Statistics Exam Questions and Answers
When preparing for assessments in the field of data analysis, it is important to focus on practical scenarios that test your ability to solve problems efficiently. The best way to prepare is by familiarizing yourself with various types of challenges, practicing solutions, and reviewing common problem formats. These exercises will help sharpen your critical thinking and analytical skills, allowing you to approach even the most difficult problems with ease.
By working through sample exercises, you can gain insight into how theoretical knowledge is applied in real-world situations. This approach not only builds confidence but also improves the ability to interpret complex data and draw conclusions based on results. Whether you’re tackling calculations, interpreting graphs, or making predictions, consistent practice is key to success.
In this section, we will explore a selection of practice tasks that cover key topics, ranging from basic principles to more advanced techniques. Each example will provide detailed explanations, helping you understand the reasoning behind each solution and prepare effectively for any challenge you may face.
Overview of Key Statistical Concepts
Understanding the foundational principles behind data analysis is essential for tackling complex challenges. Core ideas such as probability, distribution patterns, and hypothesis testing are the building blocks that guide the interpretation of numerical data. Mastery of these concepts provides the framework for solving problems and making informed decisions based on data.
Key Methods for Data Interpretation

Several methods are commonly used to analyze datasets, such as calculating measures of central tendency, variability, and correlation. These techniques help identify trends and relationships between variables, which are crucial for making predictions and drawing meaningful conclusions from data.
Importance of Probability in Analysis

Probability plays a vital role in evaluating the likelihood of events occurring. It helps to quantify uncertainty and is used in various models to make forecasts or assess risks. Understanding probability theory enhances the ability to evaluate outcomes and supports decision-making processes across different fields.
Common Topics in Applied Statistics Exams

In assessments focused on data analysis, certain themes frequently arise, testing a wide range of skills and knowledge. These topics typically revolve around the ability to interpret data, apply mathematical models, and draw conclusions based on numerical evidence. Being familiar with these areas ensures you are well-prepared for any challenge that may come up.
One common area involves understanding various probability distributions, such as normal, binomial, and Poisson. These distributions are essential for modeling real-world phenomena and making predictions about random events. Mastery of these concepts allows you to identify patterns and analyze the likelihood of specific outcomes.
Another frequent topic is regression analysis, which focuses on examining relationships between variables. Knowing how to perform and interpret linear and multiple regressions is critical for understanding how changes in one variable affect another. This skill is widely applied in fields ranging from economics to social sciences.
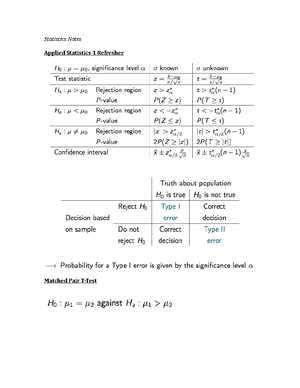
Understanding Hypothesis Testing in Exams

Hypothesis testing is a fundamental technique used to make inferences about populations based on sample data. In assessments, this method is essential for evaluating whether the evidence supports a particular claim or theory. By testing assumptions, you can determine if a hypothesis holds true or if further investigation is needed.
At the core of hypothesis testing lies the null hypothesis, which represents a statement of no effect or no difference. The alternative hypothesis, on the other hand, suggests that there is a significant effect or difference. Through rigorous testing, you evaluate the strength of evidence against the null hypothesis, often using a significance level to determine whether to reject it.
Understanding the different types of errors, such as Type I and Type II, is also crucial. A Type I error occurs when a true null hypothesis is incorrectly rejected, while a Type II error happens when a false null hypothesis is not rejected. Balancing these errors is key to making accurate conclusions based on the data.
How to Solve Probability Problems Effectively
Solving probability problems requires a clear understanding of basic principles and logical thinking. To approach these problems effectively, it’s important to break down complex situations into manageable parts. Recognizing patterns, applying formulas, and using systematic methods can help streamline the process and lead to accurate results.
Here are some steps to follow when working through probability challenges:
- Identify the problem type – Understand whether you are dealing with a simple probability, conditional probability, or a more complex scenario such as Bayes’ Theorem.
- Define the events – Clearly state the events you are interested in, and determine whether they are independent or dependent.
- Use appropriate formulas – Depending on the problem, apply the correct formula, whether it’s for combinations, permutations, or general probability calculations.
- Calculate step by step – Break down the calculations into smaller, easier steps to avoid errors and ensure clarity in your work.
- Double-check your results – Review your final answer to ensure it makes sense in the context of the problem.
By following these steps, you can increase your efficiency in solving probability problems and avoid common mistakes. Consistent practice and familiarization with various types of problems are essential for mastering this area of study.
Working with Statistical Distributions

Understanding different distribution models is crucial for analyzing data and making predictions. Distributions describe how values are spread across a dataset and help us understand patterns, variability, and the likelihood of specific outcomes. Mastering these models allows you to perform more accurate analyses and interpret results more effectively.
Types of Common Distributions
There are several types of distributions that are commonly encountered, including normal, binomial, and Poisson. Each type serves a different purpose and is useful in various scenarios. For example, the normal distribution is often used when dealing with continuous data that is symmetrically distributed, while the binomial distribution is ideal for modeling binary outcomes, such as success or failure.
How to Work with Distributions

To effectively work with these models, it’s important to understand their key properties, such as mean, variance, and standard deviation. These measures help quantify the central tendency and spread of the data. Additionally, applying the correct distribution formula to calculate probabilities is essential for making informed decisions based on the data.
Regression Analysis Question Tips
When tackling problems related to regression models, it is important to understand both the underlying theory and the practical steps involved in constructing and interpreting models. These types of problems often test your ability to identify relationships between variables, perform calculations, and interpret results accurately. Proper preparation helps ensure that you can confidently approach any regression-related task.
Understanding the Model Structure
Regression models typically involve two or more variables, with one acting as the dependent variable and others as independent predictors. To approach these questions, begin by understanding the structure of the model. Identify which variables are being measured, what assumptions are being made, and how the data is expected to behave. This foundational knowledge will help you decide which type of model to use and what steps to follow in your analysis.
Interpreting Coefficients and Significance

Once the model is constructed, the next task is to interpret the coefficients, which represent the relationship between the independent variables and the dependent variable. Be sure to focus on understanding how changes in the predictor variables affect the outcome. Additionally, evaluating the statistical significance of these coefficients is crucial for determining which variables are most influential. Always check p-values, confidence intervals, and other diagnostic tools to assess the validity of the model.
Interpreting Results from Statistical Software
Using statistical software is essential for conducting complex data analyses quickly and accurately. However, the challenge often lies not in running the analysis itself, but in interpreting the output correctly. Understanding how to read the results and extract meaningful insights is crucial for making informed decisions based on data.
When interpreting software output, start by focusing on the key metrics and tests relevant to your analysis. For example, look for the coefficients in regression models to understand the relationship between variables, and pay attention to p-values to assess statistical significance. These values guide you in determining whether the observed patterns are due to chance or represent a real effect.
It is also important to evaluate the goodness of fit, often represented by measures like R-squared. This statistic tells you how well the model explains the variability in the data. Additionally, examine any diagnostic plots provided by the software to check for potential issues, such as outliers or violations of assumptions.
Key Formulas to Memorize for Exams

When preparing for assessments that involve numerical data analysis, knowing key formulas is essential. These formulas serve as the backbone for solving a wide range of problems, from calculating averages to testing hypotheses. Having a solid grasp of these equations allows you to approach challenges with confidence and efficiency.
Basic Formulas for Data Analysis
One of the first formulas to know is the mean, which is the sum of all values divided by the total number of values. This is fundamental for understanding the central tendency of your data. Another crucial formula is the variance, which measures how much the data points differ from the mean. Variance plays an important role in understanding the spread of data and is necessary for further analyses, such as standard deviation calculations.
Formulas for Regression and Hypothesis Testing
For regression analysis, the formula for the least squares method is vital for finding the best-fitting line to a set of data. It allows you to predict outcomes based on the relationship between variables. Additionally, hypothesis testing often involves the use of the z-score or t-statistic, depending on the sample size. These formulas help assess whether the results from your sample are statistically significant and support or refute your hypotheses.
Practice Problems for Applied Statistics

One of the best ways to prepare for any analysis-related task is through practice. Solving a variety of problems allows you to apply theoretical knowledge in real-world scenarios, reinforcing concepts and sharpening your problem-solving skills. Working through different types of problems helps you become familiar with the types of challenges you might face and equips you with strategies to approach them effectively.
Here are some examples of problems you can practice:
- Data Summarization – Given a dataset, calculate the mean, median, mode, range, and standard deviation to summarize its central tendency and variability.
- Probability Calculations – Use probability rules to solve problems involving multiple events, such as compound probabilities, conditional probability, and Bayes’ Theorem.
- Regression Analysis – Fit a regression model to a dataset and interpret the coefficients, R-squared value, and p-values to assess the relationship between variables.
- Hypothesis Testing – Perform hypothesis tests, such as z-tests and t-tests, to evaluate claims about population parameters based on sample data.
- Confidence Intervals – Calculate confidence intervals for means and proportions to estimate the range of values within which the true parameter lies.
By working through these problems, you can gain the experience needed to approach similar challenges in any context with confidence and precision. Practice also helps identify areas where further study is needed, allowing you to target specific skills for improvement.
Exam Strategy for Time Management
Effective time management during assessments is essential for ensuring that you can answer all tasks thoroughly and thoughtfully. Having a clear plan for how you will allocate time to different sections of the task allows you to focus on each challenge without feeling rushed. A structured approach not only helps you manage pressure but also ensures that you make the best use of the time available.
How to Divide Your Time

One of the most effective strategies is to divide the available time based on the weight and difficulty of each section. It’s important to assess the length and complexity of the task to ensure that you can allocate enough time to each part. For example, if a section is worth more points or requires detailed calculations, it may warrant more time than a shorter, less complex task.
| Section | Time Allocation | Reason |
|---|---|---|
| Short Answer | 15 minutes | These are typically quicker to complete and should be answered with concise but accurate information. |
| Data Analysis | 30 minutes | Requires detailed calculations and interpretation of results, making it more time-consuming. |
| Long Answer/Essay | 45 minutes | Needs thoughtful analysis, argumentation, and clear explanations. Allocate enough time for clear writing. |
Techniques for Staying on Track
To avoid spending too much time on any one section, consider using a timer or watch to track your progress. Regularly check the clock to ensure that you’re not spending more time than necessary on any given task. If you find yourself stuck on a particularly difficult question, move on and come back to it later if possible. Prioritize sections that carry more weight and leave shorter, easier tasks for the end.
Understanding Data Collection Methods
In any analysis, the way data is gathered plays a crucial role in the reliability and accuracy of the conclusions drawn. Various techniques for obtaining information are used depending on the research objectives, the nature of the data, and the available resources. Understanding these methods ensures that the right approach is applied to collect high-quality, relevant data for any task.
Here are some common methods for gathering data:
- Surveys – A widely used technique where individuals are asked a set of standardized questions. This method is efficient for collecting large amounts of data from diverse groups.
- Interviews – In-depth, personal conversations that allow for detailed responses and the exploration of complex topics. Interviews are often used when qualitative insights are needed.
- Observations – Directly observing subjects or phenomena in their natural environment. This method is particularly useful for collecting behavioral data.
- Experiments – Controlled settings where variables are manipulated to observe effects. This method is commonly used in scientific studies to establish cause-and-effect relationships.
- Existing Data Sources – Leveraging pre-existing datasets, such as historical records, governmental data, or databases, to extract relevant information for analysis.
Choosing the appropriate method depends on the research goals, available resources, and the type of information needed. Each technique comes with its advantages and limitations, and understanding these nuances is essential for successful data collection.
Dealing with Complex Statistical Questions
When faced with intricate tasks, it’s essential to approach them methodically to avoid feeling overwhelmed. These types of challenges often require careful breakdown and a step-by-step analysis to ensure accuracy. By dissecting the problem into manageable parts and applying logical reasoning, you can navigate even the most complicated scenarios effectively.
Here’s a general approach to handling more demanding problems:
| Step | Action | Purpose |
|---|---|---|
| 1 | Understand the Problem | Carefully read the question, identifying key information and what is being asked. |
| 2 | Identify Relevant Concepts | Determine which principles or techniques apply to the task at hand. |
| 3 | Break Down the Problem | Divide the question into smaller, more manageable subproblems. |
| 4 | Apply Appropriate Methods | Use the correct formulas, processes, or tools to solve each part. |
| 5 | Check Your Work | Review your steps and results to ensure accuracy and consistency. |
By following these steps, you can effectively tackle complex tasks with greater clarity and precision. This approach not only enhances problem-solving skills but also helps in reducing stress during the process.
Common Mistakes in Statistics Exams
When tackling complex tasks, it’s easy to make simple errors that can impact the final results. These mistakes often stem from a misunderstanding of the problem, misapplication of formulas, or overlooking key details. Identifying and addressing these common pitfalls can help improve accuracy and performance during challenging assignments.
Some frequent errors include:
- Misinterpreting the Data – Failing to accurately understand the given data can lead to incorrect conclusions. Always double-check that you fully comprehend the context before proceeding.
- Forgetting Assumptions – Many problems require assumptions to be made about distributions or sample sizes. Forgetting these can invalidate results.
- Incorrect Use of Formulas – Applying the wrong formula or misplacing variables is a common issue. Review each formula carefully before using it to ensure it fits the specific situation.
- Overlooking Units – Ignoring units of measurement can lead to calculation errors. Always check that your answers are in the correct units and scale.
- Failing to Check Results – After completing a calculation, it’s essential to verify the answer for consistency. Skipping this step can result in avoidable mistakes.
- Rushing Through Problems – Speeding through the task can lead to careless errors. Take the time to plan your approach and avoid hasty assumptions.
By being mindful of these common mistakes, you can avoid many pitfalls and improve the quality of your work. Careful attention to detail and systematic checking are essential to achieving reliable results.
How to Approach Multivariable Problems
When confronted with problems that involve multiple variables, it’s important to break the task down into manageable steps. These types of challenges often require a deeper understanding of how different factors interact with one another. With a structured approach, it’s possible to simplify even the most complex scenarios and find clear solutions.
Here are some strategies to effectively tackle multivariable problems:
- Identify the Variables: Start by listing all the variables involved and understanding their relationships. Determine which are independent and which are dependent.
- Understand the Context: Make sure you grasp the real-world meaning behind the variables. Context will help guide your decisions on which relationships to focus on.
- Choose the Right Method: Different problems require different approaches. Decide whether you need to use linear regression, correlation analysis, or other advanced techniques to explore the relationships between variables.
- Consider Interactions: Be aware that variables may not act independently. Look for interactions between them, as these can significantly affect the results.
- Break Down the Problem: Divide the problem into smaller sub-problems. Address each relationship or component individually before combining them for a final solution.
- Verify the Model: Once you’ve applied a model or method, check the results for consistency and logical coherence. Ensure that your solution fits the data and context correctly.
By systematically analyzing each component and selecting appropriate methods, tackling multivariable challenges becomes more straightforward. The key is to approach the task with a clear plan and attention to the relationships between different factors.
Reviewing Sample Questions and Answers
One of the best ways to prepare for challenges involving data analysis and interpretation is to practice with example problems. By working through sample scenarios, you can gain insight into the types of problems you may encounter and how to approach them systematically. This method also helps in understanding the logic behind various solutions, making it easier to tackle unfamiliar situations in the future.
Key Strategies for Reviewing Practice Problems
When reviewing sample problems, it’s essential to focus on the following strategies:
- Understand the Problem Context: Before jumping into calculations, take a moment to grasp the context of the problem. Identify key variables and understand how they relate to each other.
- Break Down the Steps: Solve each problem step-by-step. Avoid rushing through calculations–focus on understanding each phase of the solution.
- Focus on Common Patterns: Many problems follow common patterns or methods of resolution. Recognize these patterns to speed up your process in real scenarios.
- Check Your Work: After completing a solution, always review your steps to ensure there are no mistakes in the logic or calculations.
- Seek Alternate Methods: If the problem allows, experiment with different approaches. This broadens your understanding and prepares you for a variety of challenges.
Why Reviewing Samples Is Important
By reviewing sample problems and their solutions, you’ll improve both your problem-solving skills and your understanding of essential concepts. This practice not only boosts your confidence but also helps in refining your approach to similar tasks in the future.