
In every educational journey, tackling challenging topics and mastering complex concepts plays a crucial role in student success. For those diving into higher levels of learning, having access to reliable solutions can make a world of difference. With the right resources, learners can break down intricate exercises, gain clarity, and strengthen their understanding. This section offers a detailed overview to help students navigate through difficult lessons with confidence.
Effective resources provide more than just solutions–they offer explanations, step-by-step breakdowns, and strategies for mastering each problem. By carefully studying these resources, students can improve their skills and ensure a deeper grasp of the material. Whether you’re reviewing individual exercises or preparing for assessments, these tools are designed to guide you through every stage of learning.
Understanding how to use these resources properly is key to maximizing their potential. With a thoughtful approach, learners can tackle every question and find the paths to success, reinforcing their knowledge and boosting their academic performance.
Comprehensive Solution Guide for Complex Problems
For students facing difficult challenges in higher-level coursework, having access to a reliable set of solutions can significantly enhance their understanding. A structured approach to solving problems not only aids in finding correct answers but also reinforces the methods needed to approach future exercises. This section offers a detailed reference for solving key problems, ensuring that learners gain clarity and confidence in their studies.
By breaking down complex tasks into manageable steps, students can develop the skills necessary to approach similar questions with ease. A well-organized solution guide helps learners connect theoretical knowledge with practical application, making it an indispensable tool in mastering advanced topics.
| Problem | Solution | Method |
|---|---|---|
| Equation 1 | 12x + 5 = 17 | Solve for x |
| Equation 2 | x^2 – 9 = 0 | Factor and solve for x |
| Word Problem 1 | Calculate the total cost | Apply the correct formula |
Overview of the Educational Series
The educational series aims to provide a comprehensive framework for mastering complex subjects, helping students progress through challenging levels of learning. This approach focuses on building a strong foundation through structured lessons that promote critical thinking and problem-solving skills. Each unit is designed to foster understanding, encourage practice, and support long-term retention of concepts.
The curriculum is designed with a clear progression, guiding learners through various topics while providing consistent opportunities for review and application. By gradually increasing the level of difficulty, the series ensures that students can build their skills at their own pace, reinforcing key concepts along the way.
Through interactive exercises, real-world applications, and detailed explanations, the series offers a dynamic learning experience that helps students not only solve problems but also develop the tools necessary for success in higher education and beyond.
Understanding the Advanced 2 Curriculum
The curriculum is designed to challenge learners by introducing more complex topics and helping them refine their problem-solving abilities. It focuses on deepening the understanding of essential concepts while encouraging critical thinking and the application of knowledge to real-world scenarios. With each lesson, students develop a more thorough grasp of the material, preparing them for future academic challenges.
This approach involves a combination of theoretical learning and practical exercises, ensuring that students can apply what they’ve learned in various contexts. The goal is not only to cover the material comprehensively but also to make sure that students are equipped with the necessary tools to approach advanced topics confidently.
| Topic | Description | Skills Developed |
|---|---|---|
| Linear Equations | Solving equations with one or more variables | Critical thinking, algebraic manipulation |
| Functions | Understanding relationships between variables | Graphing, interpretation, functional analysis |
| Polynomials | Working with expressions involving powers of variables | Factoring, expansion, simplifying expressions |
How to Use the Solution Guide Effectively

Utilizing a solution guide properly can significantly enhance a student’s learning process. It is not just about finding the right answers, but understanding the reasoning behind each step. When used correctly, such resources help reinforce concepts and foster a deeper understanding of complex topics. Here are some strategies to make the most of a solution guide:
- Review Before Checking: Attempt to solve the problem on your own first. Use the guide only after you have made an effort to reach the solution independently.
- Understand Each Step: Focus on the explanation behind each solution step, not just the final result. This approach helps build a stronger foundation.
- Identify Mistakes: If your solution differs from the guide, carefully compare each step to identify where you went wrong. This helps in recognizing gaps in your understanding.
- Practice Similar Problems: After reviewing the solution, try similar exercises to reinforce the learned methods and techniques.
- Use It as a Teaching Tool: If you have trouble understanding a concept, break down the steps as if teaching someone else. This can help clarify any confusion.
By following these steps, students can transform a simple solution guide into a powerful tool for mastering difficult subjects and gaining confidence in their academic abilities.
Key Features of the Solution Guide

A comprehensive solution guide offers a range of essential features that support learners in mastering challenging concepts. It goes beyond simply providing solutions; it includes detailed explanations and step-by-step breakdowns, ensuring that students not only know the right answers but also understand the reasoning behind each step. These guides are designed to promote a deeper level of comprehension and improve problem-solving abilities.
Step-by-Step Explanations
Each solution is accompanied by a clear, logical explanation that helps students grasp the underlying principles. This method ensures that learners are not just memorizing answers, but actively engaging with the material.
Multiple Problem Types
The guide covers a wide range of problem types, providing solutions for various formats and difficulties. This diversity helps students prepare for a variety of challenges, ensuring they are well-equipped to handle any task that may arise.
Common Challenges in Advanced 2 Math
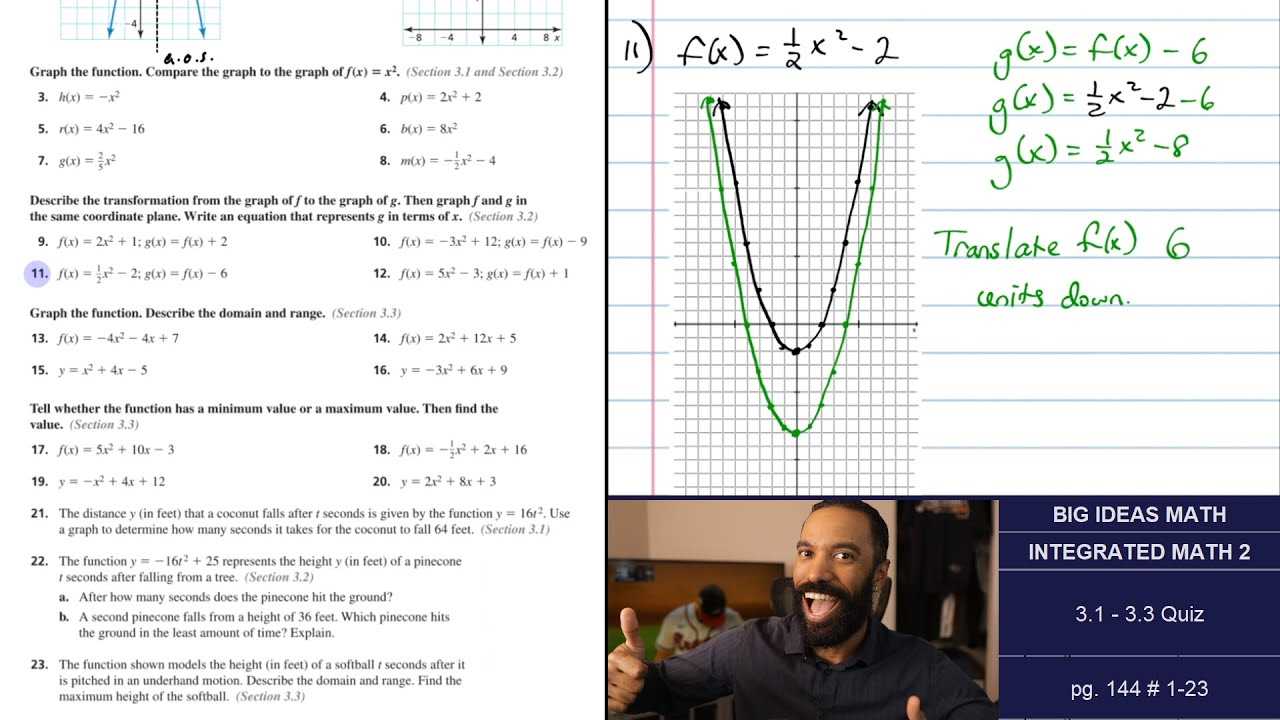
As students move into higher levels of study, they often encounter more complex problems that require a deeper understanding of the subject. These challenges can range from mastering difficult concepts to applying advanced techniques in problem-solving. Recognizing and addressing these obstacles early on can significantly improve performance and confidence. Below are some of the most common difficulties students face in more advanced coursework.
Understanding Complex Equations
One of the most significant hurdles is solving intricate equations that involve multiple variables and operations. Many students struggle with keeping track of different terms and applying the correct operations, which can lead to errors in their solutions. It’s crucial to break these problems into smaller, more manageable steps to avoid confusion.
Grasping Abstract Concepts
Advanced topics often introduce abstract concepts that are harder to visualize or relate to real-life scenarios. Understanding these theoretical ideas requires a strong foundation in the basics and the ability to think critically about how concepts connect with one another. Practice and repetition are key to mastering these more abstract aspects of the subject.
Step-by-Step Problem Solving Techniques
Approaching complex problems systematically is essential for achieving success in higher-level coursework. By breaking down problems into smaller, manageable parts, students can reduce confusion and enhance their ability to reach the correct solution. Here are some effective techniques to solve challenging exercises step by step:
- Read the Problem Carefully: Understand what is being asked and identify the key information. Make sure you know the goal before starting any calculations or steps.
- Identify Known and Unknown Values: List the given data and what you need to find. This will help you decide which methods or formulas to apply.
- Choose the Right Approach: Depending on the type of problem, select the most appropriate method–whether it’s solving an equation, graphing, or using algebraic manipulation.
- Work Through Each Step: Follow the necessary steps without skipping any. If you encounter difficulties, try breaking the problem down further or recheck your earlier steps.
- Verify Your Solution: After solving, go back through your solution to ensure the result makes sense and matches the requirements of the problem.
By following these structured steps, students can build their confidence and approach each new problem with a clear, logical method, leading to better outcomes and deeper understanding.
Solving Equations in Higher-Level Coursework
Solving equations is a fundamental skill in advanced studies, as it forms the basis for understanding more complex concepts. By mastering different types of equations, students can develop problem-solving strategies that are applicable across various topics. This section covers the key techniques and strategies to effectively solve equations in challenging coursework.
- Identify the Type of Equation: Determine if the equation is linear, quadratic, or involves other operations. Understanding the type of equation helps in selecting the appropriate solving method.
- Isolate the Variable: Begin by isolating the variable on one side of the equation. This typically involves using inverse operations such as addition, subtraction, multiplication, or division.
- Simplify the Equation: Combine like terms and simplify both sides of the equation to make it easier to solve. This may include factoring or expanding expressions as needed.
- Check for Solutions: After solving for the variable, substitute the solution back into the original equation to verify its correctness. This ensures that no errors were made during the solving process.
- Consider Special Cases: Be aware of special cases, such as no solution or infinitely many solutions, which may arise in certain types of equations, especially in systems of equations.
By following these strategies, students can approach equations with confidence and develop the skills needed to tackle more complex mathematical challenges.
Application of Advanced 2 Concepts
Understanding the practical applications of complex concepts is crucial for mastering higher-level subjects. These concepts are not only theoretical but can be applied to solve real-world problems. By learning how to use advanced techniques in various contexts, students can enhance their critical thinking skills and see the value of their studies beyond the classroom.
For example, topics like algebraic manipulation, functions, and problem-solving strategies are often used in fields such as engineering, economics, computer science, and data analysis. Recognizing how these concepts are applied in real-world scenarios helps students understand their relevance and prepares them for future academic or professional endeavors. Whether it’s modeling financial trends or designing technological systems, the ability to apply these ideas can lead to innovative solutions and deeper insights.
Improving Skills with Solution Guides
Using solution guides effectively can significantly enhance a student’s ability to solve complex problems. Rather than merely providing the correct answers, these resources offer detailed explanations that help students understand the reasoning behind each step. By reviewing the solutions and understanding the methods used, learners can strengthen their problem-solving techniques and build a solid foundation in their studies.
Solution guides allow students to identify where they might have gone wrong, providing valuable insights into their mistakes. This process of self-correction encourages active learning and promotes a deeper understanding of the concepts involved. Additionally, students can use these guides as a tool to practice similar problems, reinforcing the techniques and strategies needed to tackle new challenges with confidence.
How the Solution Guide Supports Learning
Solution guides are invaluable tools that can greatly enhance a student’s learning experience. Rather than just providing the final solution, they offer step-by-step explanations of how each problem is solved. This helps learners develop a deeper understanding of the underlying principles and techniques used to reach the correct answers, fostering stronger problem-solving skills and critical thinking.
Clarifying Concepts
One of the primary benefits of using a solution guide is its ability to clarify difficult concepts. By following the detailed steps and seeing how each concept is applied, students can make connections between theory and practice. This clear explanation helps transform abstract ideas into more tangible knowledge that can be applied in a variety of scenarios.
Building Confidence
Another key benefit is that solution guides help build a student’s confidence. When students struggle with a particular problem, the guide provides them with a clear path to the solution, allowing them to understand where they made mistakes and how to correct them. This process of self-correction leads to a greater sense of mastery and the ability to approach similar problems with more confidence in the future.
Analyzing Word Problems in Higher-Level Coursework
Word problems are a key aspect of learning that requires students to translate real-world situations into mathematical expressions and solutions. By carefully analyzing these problems, students can improve their ability to break down complex scenarios and solve them step by step. This skill is essential in many academic and professional fields, as it fosters both logical reasoning and problem-solving abilities.
- Read the Problem Thoroughly: Begin by carefully reading the entire word problem. Understanding the context and identifying the key information is the first step in formulating a solution.
- Identify Key Variables: Look for numbers, operations, and other important details that may define the variables in the problem. This allows for a structured approach to solving the problem.
- Break the Problem Into Parts: Divide the problem into smaller, more manageable sections. Solving each part separately helps maintain focus and prevents confusion.
- Choose the Appropriate Approach: Determine the best mathematical method to solve the problem, such as algebraic equations, geometry, or data analysis. The right approach will depend on the specifics of the problem.
- Double-Check the Solution: After solving, revisit the problem to ensure the solution makes sense within the context. Verifying the answer helps confirm its correctness and prevents errors.
Mastering the ability to analyze and solve word problems is essential for excelling in more complex subjects. With practice, students can develop the skills needed to approach challenges with greater confidence and efficiency.
Tips for Mastering Complex Problems

Mastering complex problems requires both strategic thinking and a methodical approach. It’s essential to break down challenging tasks into smaller, manageable steps and develop a solid understanding of the fundamental concepts involved. By following a structured process, students can gradually build confidence and proficiency in tackling even the most difficult problems.
Here are some effective strategies for approaching complex problems:
| Step | Tip |
|---|---|
| 1 | Understand the Problem: Before attempting to solve a problem, take the time to fully understand its requirements and what is being asked. Identify key information and any constraints provided in the prompt. |
| 2 | Break It Down: Divide the problem into smaller, simpler sections. Tackle each section individually, which helps avoid feeling overwhelmed by the complexity of the task. |
| 3 | Choose the Right Strategy: Determine which method or approach is most appropriate for solving the problem. Whether it’s using algebra, geometry, or other techniques, selecting the right tools is crucial for success. |
| 4 | Work Step by Step: Solve the problem step by step, carefully checking each stage. Avoid jumping ahead or skipping steps, as this can lead to mistakes. |
| 5 | Review and Verify: After reaching a solution, review your work and verify that the answer makes sense. Double-check calculations and reasoning to ensure accuracy. |
By practicing these techniques consistently, students can develop a structured approach to problem-solving that will help them succeed in tackling even the most complex challenges with ease.
Using the Answer Key for Self-Study
Self-study is an essential aspect of mastering complex subjects, allowing individuals to learn at their own pace. When utilizing a solution guide, it’s important to approach it as a tool for reinforcing understanding, rather than simply checking answers. By carefully analyzing the solutions provided, learners can uncover effective methods for solving problems and gain insight into their areas of weakness.
Effective Strategies for Self-Study
To maximize the benefits of using a solution guide during independent study, here are some helpful techniques:
- Check Your Work: After solving a problem, compare your solution with the provided one. Analyze any discrepancies to understand where your approach may have been incorrect.
- Focus on Mistakes: When you encounter errors, don’t simply gloss over them. Take time to understand the mistake, correct it, and ensure that the same error does not occur again.
- Study Different Methods: If multiple solution methods are available, try to understand and practice each one. This will expand your problem-solving toolkit and provide flexibility in tackling various types of questions.
- Reinforce Concepts: Use the solution guide to reinforce key concepts that might be unclear. The explanations provided can offer a deeper understanding of specific techniques or strategies.
- Work Regularly: Consistent practice is key to improving your skills. Use the solution guide to ensure that you are progressing in the right direction and gradually mastering more complex problems.
Avoid Over-reliance

While the solution guide is a valuable resource, it’s important not to rely on it too heavily. Using the guide as a crutch can hinder independent problem-solving skills. Strive to work through problems on your own first, and only consult the guide when necessary to check your understanding or resolve difficult concepts.
Answer Guide’s Role in Exam Preparation
Effective preparation for exams requires a combination of practice, self-assessment, and understanding. A solution guide plays a significant role in this process by providing immediate feedback and clarifying the steps required to reach correct solutions. By reviewing detailed explanations and step-by-step solutions, students can reinforce their understanding and identify areas that need improvement before the exam.
Using a solution guide during preparation can help familiarize students with the types of questions they might encounter and ensure they are comfortable with various problem-solving strategies. It also acts as a valuable resource when students need to verify their approach and results, offering insights into efficient techniques and methods for tackling challenging problems.
However, it is important to balance using the guide with independent problem-solving. Relying solely on the guide can limit the development of critical thinking and problem-solving skills. Instead, the guide should serve as a supplementary tool, enhancing learning while encouraging active engagement with the material.
Exploring Additional Resources for Success

Achieving academic success often involves more than just completing assignments and reviewing lesson materials. To deepen understanding and sharpen skills, it’s important to explore a range of supplementary resources that can provide additional perspectives and practice. These resources can offer different approaches to problem-solving and new techniques for mastering difficult concepts.
While textbooks and solution guides are invaluable, students can benefit from a variety of other tools, such as online tutorials, practice exercises, educational videos, and interactive apps. These platforms can offer immediate feedback and tailored instruction, helping learners reinforce their knowledge in a dynamic and engaging way.
Additionally, collaborating with peers or seeking help from instructors can provide clarity on challenging topics. Group study sessions and one-on-one tutoring are excellent ways to discuss problems and share strategies for effective learning.
| Resource | Benefit |
|---|---|
| Online Educational Platforms | Interactive lessons and practice problems |
| Study Groups | Collaborative problem-solving and peer support |
| Tutorial Videos | Visual explanations of complex topics |
| Practice Apps | Real-time feedback and progress tracking |
When to Seek Teacher Assistance
There are times when independent study and practice may not be enough to overcome challenges in learning. Recognizing when to seek help from an instructor can make a significant difference in understanding difficult topics and improving overall performance. Teachers are an invaluable resource for clarification, guidance, and personalized support in areas where students might struggle.
It’s important to ask for assistance when a concept remains unclear after multiple attempts at self-study. Teachers can provide alternative explanations, offer additional examples, or break down complex ideas in a way that resonates with individual learning styles. Early intervention is key–waiting until just before an exam or assignment deadline may make it harder to fully grasp the material.
When to Ask for Help
- When you feel stuck on a specific concept or topic.
- If repeated practice doesn’t lead to improvement or understanding.
- When you notice gaps in your knowledge that affect future lessons.
- If you’re unsure of the correct method or process to solve problems.
How to Approach Your Teacher

- Be clear about the specific areas where you need help.
- Ask focused questions to guide the conversation.
- Be open to feedback and suggestions for improvement.
- Take notes during the discussion to reference later.
Final Thoughts on Big Ideas Math Advanced 2
As students progress through their educational journey, mastering complex topics becomes increasingly essential. The curriculum designed for higher-level learning serves as a foundation for developing critical problem-solving skills and a deeper understanding of mathematical principles. By utilizing available resources effectively, such as practice materials and teacher support, learners can confidently tackle these challenging subjects and build lasting knowledge.
The materials provided are structured to enhance comprehension and provide diverse approaches to solving problems. Through consistent practice and reflection, students can strengthen their grasp of difficult concepts and refine their problem-solving abilities. The key to success lies in persistence, asking for help when necessary, and utilizing the right tools to complement the learning process.
Key Takeaways
- Consistent practice and review are crucial for mastering complex topics.
- Understanding the core concepts leads to better application in problem-solving.
- Seeking teacher assistance when stuck can clarify doubts and strengthen understanding.
- Additional resources, like practice problems and online tutorials, are valuable tools for success.
Moving Forward
- Approach challenging problems with a positive mindset and persistence.
- Set realistic learning goals and review progress regularly.
- Remember that every mistake is an opportunity to learn and improve.