Mathematics is a cornerstone of logical thinking and analytical reasoning. Developing a strong understanding of its principles enables learners to approach challenges systematically and find effective solutions. A focus on foundational concepts is essential for building confidence and achieving better results in assessments.
Effective preparation includes practicing diverse types of problems, understanding relationships between variables, and mastering the methods needed to simplify and solve equations. These skills not only help in exams but also contribute to a deeper appreciation of how numbers and formulas interact in real-world applications.
This resource offers practical insights, proven strategies, and clear examples designed to guide learners through key topics. By focusing on structured learning and continuous practice, you can strengthen your mathematical foundation and perform confidently in any test environment.
Essential Topics for Algebra 1 EOC
Mastering key mathematical principles is crucial for developing strong problem-solving abilities. A comprehensive understanding of fundamental topics provides the groundwork for tackling more complex challenges and performing well in exams.
One critical area includes working with linear relationships, where recognizing patterns and interpreting graphical data are essential skills. Equally important is understanding how to solve and manipulate equations involving variables to find accurate solutions efficiently.
Another focus is the study of quadratic functions, where learners explore parabolic shapes and their properties. Factoring and simplifying expressions also play a major role, helping to break down seemingly complicated problems into manageable steps.
Additional topics include working with inequalities, analyzing their solutions on number lines, and applying these techniques to real-world scenarios. Strengthening these areas ensures a well-rounded grasp of mathematical concepts and prepares students for future challenges.
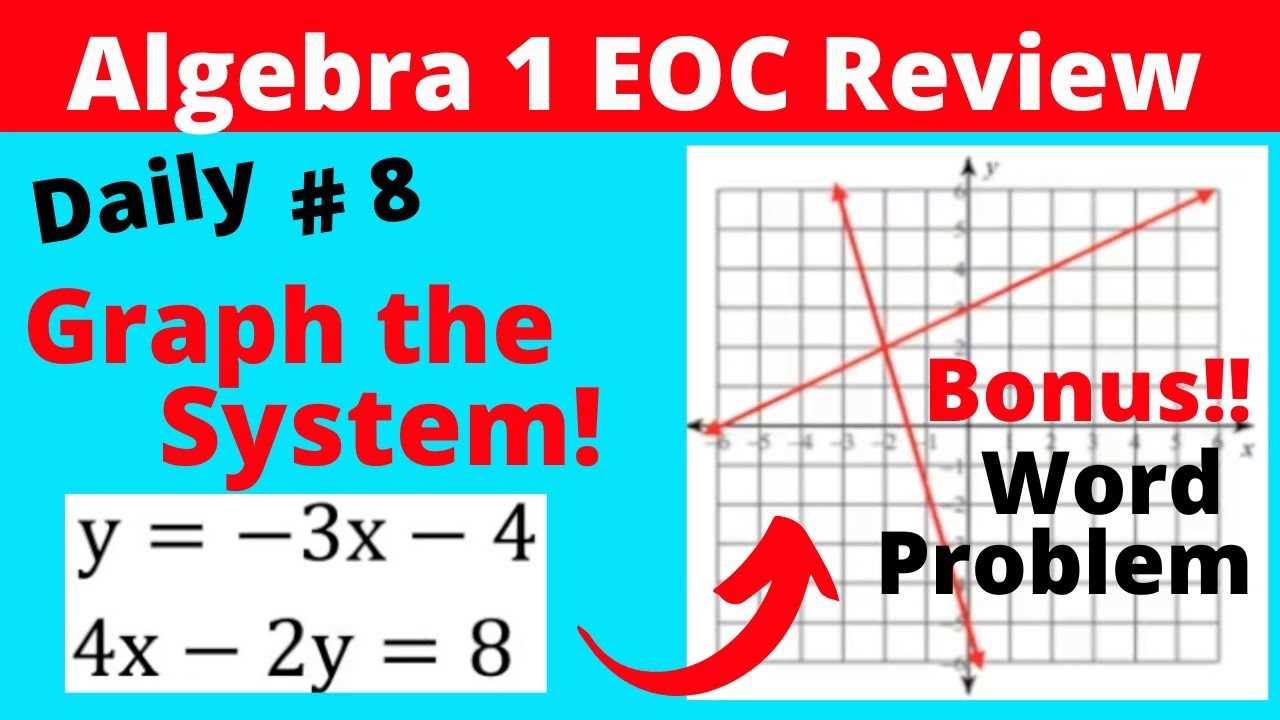
How to Solve Linear Equations Easily
Solving equations with one variable is a fundamental skill that requires understanding the relationship between numbers and operations. The goal is to find the value of the unknown by isolating it through logical steps. With practice, solving these equations can become an intuitive process that is easy to master.
Step-by-Step Approach
Start by simplifying both sides of the equation. Combine like terms and eliminate any parentheses, if present. This helps create a simpler equation to work with, making the next steps more straightforward.
Next, move all terms involving the variable to one side of the equation. Use addition or subtraction to shift constants to the opposite side. The key here is to maintain balance by performing the same operation on both sides.
Check Your Solution

Once the variable is isolated, solve for its value. To ensure the accuracy of your solution, substitute it back into the original equation. If both sides are equal, your solution is correct. This verification step ensures that no mistakes were made during the process.
By following these steps, solving linear equations becomes a more manageable task, and with consistent practice, you’ll gain the confidence to solve even more complex problems efficiently.
Understanding Function Behavior and Relations
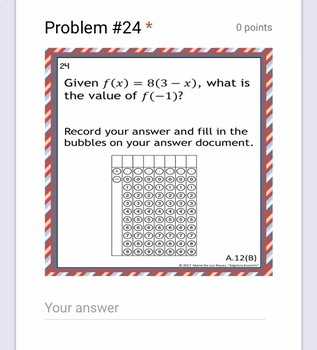
Grasping how mathematical relationships behave is crucial for analyzing and solving various types of problems. Functions are key to understanding how one quantity relates to another, and how changes in one variable affect the outcome of another. Recognizing these patterns allows for a deeper comprehension of many mathematical concepts and real-world applications.
Key Elements of Functions
- Domain: The set of possible input values (x-values) for a function.
- Range: The set of possible output values (y-values) that result from applying the function to the domain.
- Mapping: The relationship between each input and its corresponding output.
Types of Relations and Their Behavior
Different types of relations exhibit distinct behaviors. Linear relationships create straight-line graphs, while non-linear ones may form curves or more complex shapes. Understanding the general trends and behaviors of these relationships is essential for making predictions and drawing conclusions.
For example, in linear relations, as one variable increases or decreases, the other does so at a constant rate. In contrast, quadratic or exponential functions change at varying rates, creating curves that can rise or fall rapidly. Identifying the type of function is the first step in determining how it will behave.
By recognizing these patterns and relationships, you can develop a more intuitive approach to solving problems and analyzing data in mathematics.
Tips for Finding Slope and Intercepts
Determining key features of a line, such as its steepness and where it crosses the axes, is vital for understanding its behavior and relationship between variables. These elements provide valuable insights into how changes in one quantity affect another. By following a few simple techniques, you can easily identify the slope and intercepts of any linear equation.
Finding the Slope
The slope of a line indicates how steep it is, or the rate at which one variable changes relative to another. To calculate the slope, use the formula m = (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) are two distinct points on the line. This formula helps you determine the vertical change (rise) compared to the horizontal change (run) between the points.
If you are working with an equation in slope-intercept form y = mx + b, the slope is simply the coefficient of x, represented by m. This allows for quick identification of how steep the line is without needing to find individual points.
Identifying the Intercepts
The intercepts show where the line crosses the axes. The y-intercept is the point where the line crosses the vertical axis, and it is easily found by setting x = 0 in the equation. Similarly, the x-intercept occurs where the line crosses the horizontal axis, which can be found by setting y = 0.
By substituting these values into the equation, you can quickly determine the coordinates of the intercepts. This step helps to visualize how the line interacts with both axes and gives more context to the relationship between the variables.
With these simple tips, you can confidently find both the slope and intercepts of any linear equation, making it easier to analyze and interpret the behavior of the line.
Breaking Down Systems of Equations
Understanding and solving a set of equations that share common variables can be challenging, but with the right approach, it becomes manageable. These sets of equations often require finding values for the variables that satisfy all equations simultaneously. There are several methods to solve them, each offering a unique way to analyze and simplify the system.
Substitution Method
One effective method is substitution, where you solve one equation for one variable and substitute that expression into the other equation. This allows you to eliminate one variable and solve for the other. Once you find the value of one variable, you can substitute it back into the original equation to find the value of the second variable.
Elimination Method

Another method is elimination, which involves adding or subtracting the equations to eliminate one of the variables. By manipulating the equations in such a way that one variable cancels out, you can easily solve for the remaining variable. This method is especially useful when the coefficients of one variable in both equations are the same or can be made the same.
Graphical Method
For those who prefer a visual approach, the graphical method involves plotting both equations on a coordinate plane. The point where the two lines intersect represents the solution to the system. This method provides an intuitive way to understand the relationship between the equations, but it is less precise than algebraic methods.
By mastering these techniques, solving systems of equations becomes a straightforward task. With practice, you’ll be able to identify the best method for each situation and efficiently find solutions to complex problems.
Strategies for Simplifying Rational Expressions
Simplifying rational expressions involves reducing complex fractions to their simplest form, making them easier to work with in mathematical problems. The goal is to eliminate common factors from both the numerator and denominator, enabling a more straightforward solution. By applying specific techniques, you can simplify expressions and avoid unnecessary complexity.
Factorizing the Numerator and Denominator
One of the most effective strategies is to factor both the numerator and denominator. By breaking down each polynomial into its prime factors, you can identify common factors that can be canceled out. This is often the first step in simplifying any rational expression, as it simplifies the structure of the fraction and makes it easier to spot potential reductions.
Canceling Common Factors
Once you’ve factored both the numerator and the denominator, look for common factors that appear in both parts. If the same factor appears in both the numerator and denominator, it can be canceled out. This will simplify the expression significantly and eliminate unnecessary terms, leaving you with a more manageable equation.
Identifying Restrictions
When simplifying rational expressions, it’s important to identify any restrictions on the variables. For instance, certain values of the variable might make the denominator equal to zero, which would create undefined expressions. By determining these values beforehand, you can avoid mistakes in the simplification process.
By following these strategies, you can simplify even the most complicated rational expressions, turning them into simpler, more manageable forms. Mastering these techniques will improve your overall problem-solving skills and help you approach similar challenges with confidence.
Mastering Exponent Rules and Applications
Understanding the rules of exponents is essential for solving a wide range of mathematical problems. Exponents, which express repeated multiplication, play a significant role in simplifying expressions and solving equations. By mastering the basic laws governing exponents, you can streamline your work and solve complex problems with ease.
Key Exponent Rules

To efficiently simplify expressions involving exponents, it’s important to become familiar with the following rules:
- Product of Powers Rule: When multiplying two expressions with the same base, add the exponents. For example, x^m * x^n = x^(m+n).
- Power of a Power Rule: When raising an exponent to another power, multiply the exponents. For example, (x^m)^n = x^(m*n).
- Quotient of Powers Rule: When dividing two expressions with the same base, subtract the exponents. For example, x^m / x^n = x^(m-n).
- Zero Exponent Rule: Any non-zero number raised to the power of zero equals one. For example, x^0 = 1.
- Negative Exponent Rule: A negative exponent indicates a reciprocal. For example, x^-n = 1/x^n.
Applications of Exponent Rules
Exponent rules are not just theoretical; they are applied to solve real-world problems. Here are a few practical applications:
- Scientific Notation: Exponents are used to express large or small numbers in a more manageable format. For example, 6.02 x 10^23 represents Avogadro’s number in chemistry.
- Compound Interest: Exponent rules help calculate growth or decay, such as when determining the future value of an investment.
- Physics and Engineering: Exponents are used to express laws of physics, such as the laws of gravity or electrical circuits, where rates of change are often exponential.
By practicing these rules and understanding their applications, you can quickly simplify expressions and solve more complex problems. Mastery of exponents will significantly enhance your problem-solving abilities and prepare you for more advanced mathematical challenges.
Techniques for Solving Radical Equations
Solving equations involving roots, also known as radical equations, can be a challenging but rewarding process. These equations contain variables within square roots or higher-order roots, and solving them requires specific techniques to eliminate the radicals and isolate the variable. By understanding and applying these methods, you can simplify complex problems and find accurate solutions.
Here are the general steps and techniques for solving radical equations:
| Step | Explanation |
|---|---|
| Step 1: Isolate the Radical | Move all terms that do not involve a radical to the other side of the equation. |
| Step 2: Eliminate the Radical | Raise both sides of the equation to the power that corresponds to the root. For example, if you have a square root, square both sides of the equation. |
| Step 3: Simplify the Resulting Equation | After eliminating the radical, simplify the equation and solve for the variable. |
| Step 4: Check for Extraneous Solutions | Substitute the solution back into the original equation to ensure it is valid, as raising both sides of an equation can sometimes introduce incorrect solutions. |
Following these steps can help you solve most radical equations. However, it’s important to be careful with negative values and check for extraneous solutions, as squaring both sides of an equation can sometimes lead to non-valid results. Practice will make it easier to identify when to apply each step and when a solution might be extraneous.
What to Know About Absolute Value
Understanding the concept of absolute value is crucial for solving many mathematical problems. It represents the distance of a number from zero on the number line, regardless of its sign. In essence, absolute value tells us how far a number is from the origin, ignoring whether it is positive or negative.
The absolute value of a number is always non-negative. For instance, both +5 and -5 have the same absolute value of 5, because they are both 5 units away from zero. This characteristic is useful when dealing with real-world problems, as the direction (positive or negative) often does not matter, only the magnitude.
Key Points About Absolute Value:
- Notation: The absolute value of a number is denoted by two vertical bars around the number, such as |x|.
- Positive or Zero: Absolute value will always be greater than or equal to zero. For any number x, |x| ≥ 0.
- Applications: Absolute value is often used in real-world situations like calculating distances, prices, or deviations from a standard.
When working with equations or inequalities involving absolute value, it’s essential to recognize that there may be two possible solutions: one positive and one negative. This duality arises because both positive and negative numbers can have the same absolute value. Therefore, understanding how to handle this is key when solving such problems.
How to Tackle Word Problems in Math
Word problems often appear daunting, but they can be solved systematically with the right approach. The key to solving these problems is understanding the scenario described and translating it into mathematical expressions. By breaking down the information step by step, you can simplify the process and identify the solution.
One of the most important steps is to carefully read the problem. Focus on identifying the variables, key numbers, and what the problem is asking you to find. Once you’ve done that, you can create an equation or a set of operations that represent the situation. It helps to use a logical sequence of steps, ensuring that every part of the problem is addressed.
Step-by-Step Strategy for Solving Word Problems:
- Read the problem carefully: Make sure you understand the context and what the question is asking.
- Identify key information: Look for numbers, relationships, and any given conditions in the problem.
- Set up an equation: Translate the information into a mathematical expression.
- Solve the equation: Perform the necessary calculations to find the solution.
- Check your answer: Ensure that the solution makes sense in the context of the problem.
Example of a Word Problem:

| Problem | Steps to Solve |
|---|---|
| If a person buys 3 shirts at $15 each, how much will they spend? |
|
| Answer: The total cost is $45. | Solution: After completing the calculation, the solution is $45. |
By following these steps and practicing regularly, you can improve your ability to solve word problems effectively and with confidence.
Key Differences Between Linear and Quadratic
Understanding the differences between linear and quadratic relationships is essential when working with equations. These two types of expressions have distinct properties and behaviors, making them easily identifiable once you know what to look for. The most significant differences stem from the shape of their graphs, the degree of the variables, and how their values change.
Key Characteristics of Linear Equations:
- Graph: The graph of a linear equation is always a straight line.
- Degree: Linear equations have a degree of 1, meaning the highest power of the variable is 1.
- Rate of Change: The rate of change between variables is constant, leading to a consistent slope.
- Example: y = 2x + 3
Key Characteristics of Quadratic Equations:
- Graph: The graph of a quadratic equation is a curve called a parabola, which can open upward or downward.
- Degree: Quadratic equations have a degree of 2, meaning the highest power of the variable is 2.
- Rate of Change: The rate of change varies, which results in a changing slope as you move along the curve.
- Example: y = x² + 4x + 3
By understanding these key differences, it becomes easier to distinguish between linear and quadratic equations and solve them appropriately. Recognizing the type of equation you’re working with is the first step in applying the correct methods to find the solution.
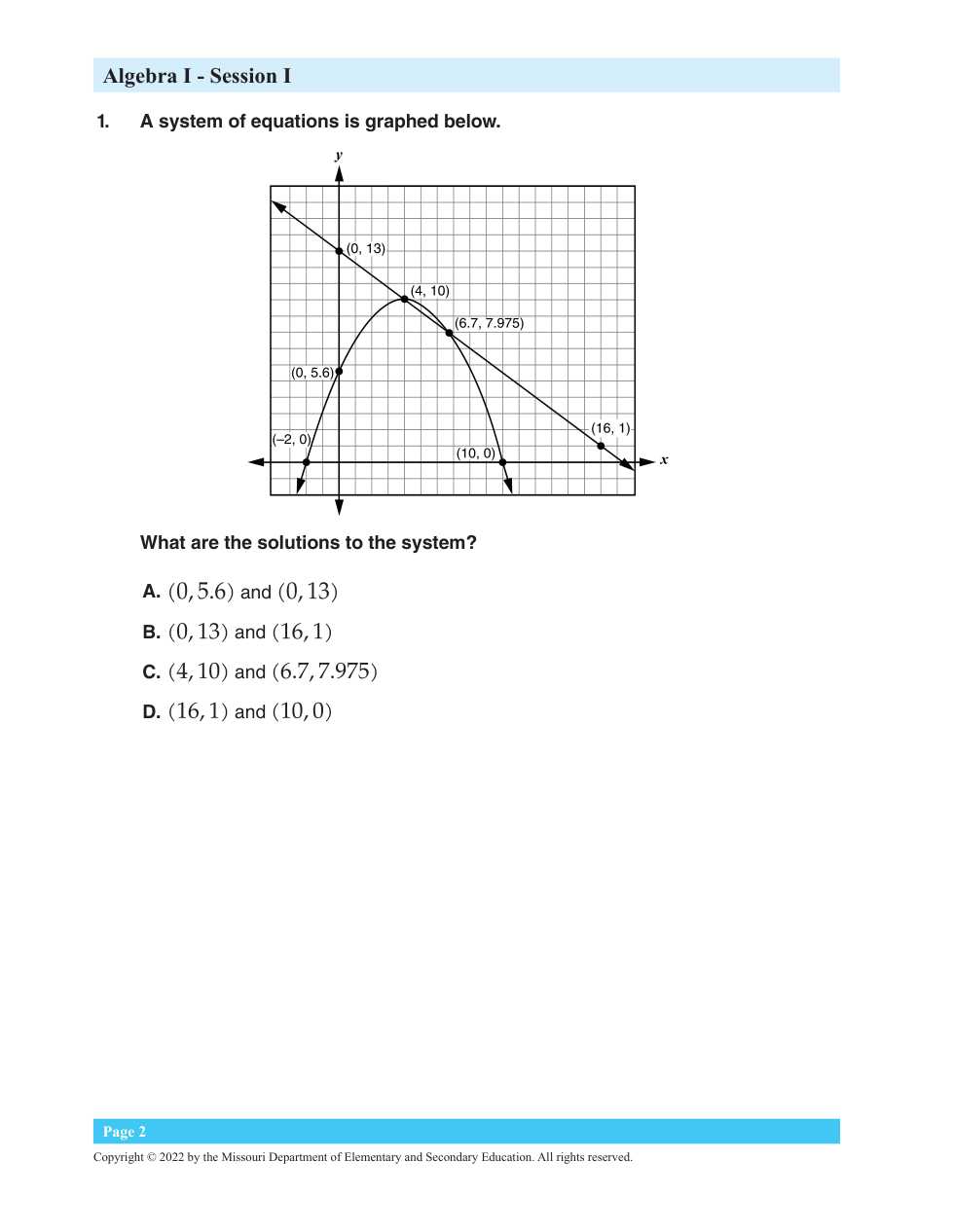
How Graphing Improves Mathematical Understanding
Graphing is a powerful tool that helps visualize mathematical concepts, making them easier to understand and solve. By translating equations into graphical representations, you can quickly identify relationships between variables and spot key features such as intersections, slopes, and symmetry. This visual approach enhances comprehension and provides a clear method for analyzing equations and functions.
When equations are graphed, abstract mathematical ideas become tangible. For example, the slope of a line can be seen as the steepness of the graph, and the y-intercept is simply the point where the line crosses the vertical axis. This ability to translate between the symbolic and visual forms of an equation can deepen understanding and facilitate problem-solving.
Moreover, graphing allows for a more intuitive understanding of changes and trends in data. It can highlight patterns, such as growth rates or decay, that are not immediately apparent in numerical form. With the aid of graphs, learners can visually track how changes in one variable affect another, reinforcing the concepts of proportionality and function.
In summary, using graphs not only strengthens mathematical skills but also builds confidence by providing a concrete way to work through abstract problems. This approach leads to a more holistic understanding, making it easier to grasp even the most complex ideas.
Checking Solutions Effectively
Ensuring the accuracy of your solutions is an essential part of the problem-solving process. Verifying your work helps confirm that the steps taken are correct and that the final answer is indeed valid. This process not only enhances your confidence in the result but also minimizes errors that may arise during calculations.
Here are a few effective strategies to check your solutions:
- Substitute the solution back into the original equation: This is one of the most reliable methods. By plugging the solution into the equation, you can verify if both sides are equal. If they match, your solution is correct.
- Use inverse operations: Reversing the steps you took to solve the equation can help confirm that the solution was derived correctly. Working backward helps catch mistakes made during the process.
- Check for extraneous solutions: In some cases, especially when working with rational or radical equations, certain solutions may not satisfy the original equation. Always test each solution to make sure it doesn’t create contradictions.
- Estimate the solution: Before checking the exact value, consider approximating the result. This can give you an idea of whether the solution makes sense within the context of the problem.
By applying these techniques, you can ensure the validity of your solutions and develop a deeper understanding of the problem-solving process. Regularly verifying your results not only helps you avoid mistakes but also improves your overall mathematical proficiency.