
In this section, we focus on providing detailed solutions to key learning challenges that students face in their fifth-year educational journey. Mastering core concepts is essential for building a strong foundation in mathematics, and this guide is designed to support learners as they tackle complex tasks. Through targeted exercises and clear explanations, students can gain a deeper understanding of the subject matter and improve their problem-solving skills.
By breaking down each question and offering step-by-step instructions, students will be able to identify the methods needed to arrive at the correct answers. This approach helps in developing critical thinking, as it encourages learners to think logically and carefully consider each problem before attempting a solution. Regular practice with such exercises ensures steady progress and fosters confidence in their abilities.
Reviewing these solutions allows students to spot any mistakes and correct them independently, enhancing their learning experience. Moreover, this process not only helps in mastering the current material but also prepares them for more advanced topics in the future. With patience and persistence, anyone can improve their mathematical proficiency.
Comprehensive Solutions for Fifth Grade Problems
This section provides a thorough breakdown of the essential exercises encountered in the fifth-year curriculum. Here, students will find detailed solutions to help them grasp core concepts and solidify their understanding. The aim is to ensure a clear and accurate path to resolving complex problems, fostering a deeper comprehension of mathematical principles.
Understanding Key Concepts and Approaches
Each task is designed to reinforce critical skills such as problem-solving, pattern recognition, and logical reasoning. By working through these exercises, learners can identify effective strategies for tackling similar challenges in the future. This section emphasizes the importance of a step-by-step approach, allowing students to develop confidence and independence as they work through problems.
Improving Problem-Solving Techniques
Revisiting each solution is a valuable tool for self-assessment. By carefully examining the correct methods and comparing them with their own attempts, students can pinpoint areas for improvement. This reflective practice strengthens their mathematical abilities and prepares them for more advanced topics ahead.
Overview of Fifth Year Learning Content
This section provides an overview of the critical concepts covered during the second segment of the curriculum for fifth-year students. The focus is on equipping learners with the necessary skills and strategies to navigate increasingly complex mathematical tasks. By exploring different topics in depth, students gain a comprehensive understanding of the material, preparing them for future academic challenges.
Core Topics Covered in the Unit
Throughout this portion of the program, students engage with key mathematical concepts such as fractions, decimals, and problem-solving techniques. These foundational skills are critical as they serve as the building blocks for more advanced topics in later grades. The section is designed to help students develop both their computational abilities and conceptual understanding, ensuring a balanced approach to learning.
Building Essential Problem-Solving Skills
In addition to understanding theoretical concepts, this section emphasizes the development of problem-solving skills. Learners are encouraged to apply their knowledge through a variety of exercises, reinforcing their ability to tackle complex problems with confidence. The practice of analyzing and solving different types of questions ensures steady improvement and prepares students for continued success in their academic journey.
Importance of Mastering Key Concepts
Mastering the fundamental concepts in this segment is essential for building a solid foundation in the subject. The skills learned here not only support current academic performance but also pave the way for success in future topics. A deep understanding of these core ideas ensures students can tackle more advanced problems with confidence and ease.
By focusing on these crucial principles, learners improve their ability to solve complex problems, think critically, and apply knowledge in a variety of contexts. Mastery of these concepts strengthens overall problem-solving skills, making future learning more manageable and rewarding.
Key Learning Objectives in the Second Segment
In this section, the focus is on mastering the essential skills and concepts that serve as the foundation for future academic success. Students are introduced to important topics that strengthen their problem-solving abilities and conceptual understanding. Achieving proficiency in these areas is critical for tackling more advanced material with confidence.
Understanding and Applying Fractions
One of the primary goals is to help students gain a solid grasp of fractions and how they relate to other mathematical concepts. Learning to add, subtract, multiply, and divide fractions is crucial for solving a wide range of problems. By mastering this skill, students can apply their knowledge to both abstract and real-world situations.
Building Confidence with Decimals
Decimals are another key focus in this segment. Students are taught how to compare, add, subtract, and multiply decimal numbers, which are essential skills in everyday life. Developing proficiency in decimals allows students to approach more complex mathematical tasks with ease and clarity.
Mastering these objectives not only enhances students’ understanding of the subject but also prepares them for future challenges. With these fundamental concepts in place, learners can approach subsequent topics with a solid mathematical foundation.
How to Use the Solution Guide Effectively
Using a solution guide properly can significantly enhance your understanding of the material and improve your problem-solving skills. It is important to not just look at the final answers, but to carefully study the steps and methods used to reach those results. This approach encourages a deeper comprehension and allows you to learn from your mistakes, strengthening your overall grasp of the subject.
Here are a few tips on how to get the most out of a solution guide:
| Step | Action | Benefit |
|---|---|---|
| 1 | Attempt problems on your own first | Develops independent problem-solving skills |
| 2 | Compare your solutions with the guide | Identifies mistakes and clarifies misunderstandings |
| 3 | Focus on the methods, not just the answers | Improves understanding of underlying concepts |
| 4 | Rework problems you struggled with | Strengthens weak areas and boosts confidence |
By following these steps, you ensure that the guide becomes a learning tool rather than just a way to check your work. This approach helps you become a more proficient learner, capable of handling even the most complex tasks with ease.
Step-by-Step Solutions for the Second Segment
This section provides detailed, step-by-step instructions for solving the key problems in the second part of the curriculum. Breaking down complex tasks into manageable steps helps learners understand the process and apply the correct methods. Each solution is carefully explained to ensure students can follow along and reinforce their learning.
Here’s how to approach each problem:
- Read the problem carefully to understand what is being asked.
- Identify the relevant concepts or operations needed to solve the task.
- Break the problem into smaller parts, solving each step one at a time.
- Check your solution against the expected result to confirm its accuracy.
- Reflect on the method used to ensure the same approach can be applied to similar problems in the future.
Following this approach helps develop a systematic problem-solving strategy that can be applied across different topics. Mastery of this process boosts confidence and ensures continued progress in learning.
Here are some example problems and their solutions:
- Problem 1: Simplify the fraction 4/8.
- Divide both the numerator and denominator by 4.
- The simplified fraction is 1/2.
- Problem 2: Add 0.25 and 0.75.
- Align the decimal points and add the numbers together.
- The sum is 1.00.
By following these steps and examples, students can tackle even the most challenging tasks with clarity and confidence.
Common Challenges in the Second Segment
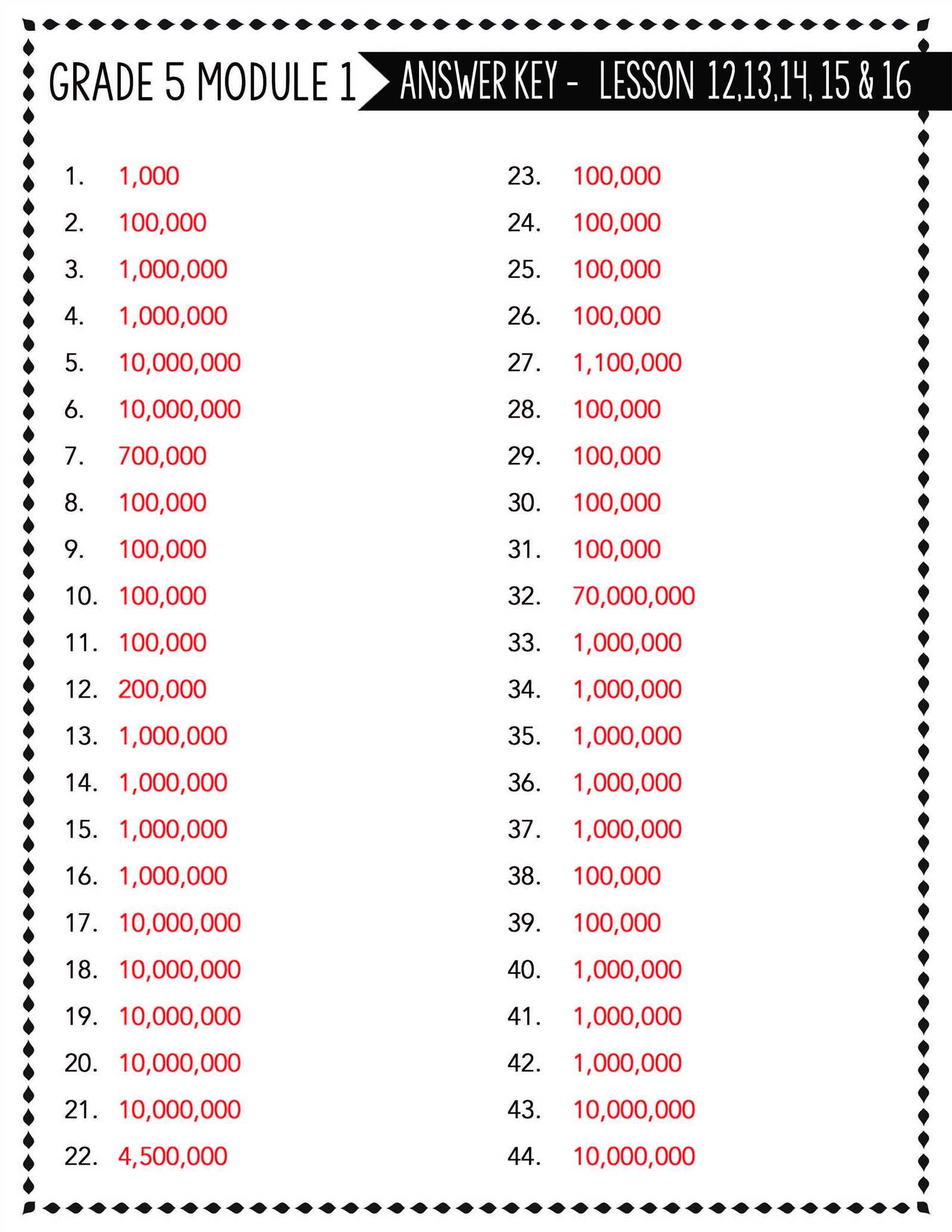
While working through this section, students may encounter several common difficulties. Understanding where these challenges arise can help learners develop effective strategies to overcome them. Addressing these obstacles early ensures better comprehension of the material and builds confidence in problem-solving abilities.
Frequent Issues and Misunderstandings
One of the most common struggles is working with fractions and decimals, especially when it comes to addition, subtraction, and conversion between the two. Many students find it difficult to grasp the relationships between numbers and operations. Another common challenge is applying learned methods to different types of problems, which requires a deeper understanding of the underlying concepts.
Strategies for Overcoming These Challenges
To tackle these issues effectively, it’s important to practice regularly and focus on understanding the steps involved rather than just memorizing formulas. Breaking problems down into smaller parts and using visual aids, like number lines or fraction models, can also help clarify confusing concepts.
| Challenge | Common Mistake | Solution |
|---|---|---|
| Working with fractions | Not finding a common denominator when adding or subtracting fractions | Always convert to the same denominator before performing operations |
| Decimal addition/subtraction | Misaligning decimal points | Ensure decimal points are aligned and work from right to left |
| Problem-solving with word problems | Focusing only on numbers, ignoring the context | Carefully read the problem and identify the key information and operations required |
By recognizing these challenges and applying the right strategies, students can overcome common obstacles and continue to make progress in their learning journey.
Understanding Word Problems in the Second Segment

Word problems can often be one of the most challenging aspects of this section, as they require not only a solid understanding of mathematical concepts but also the ability to interpret real-life scenarios. The key to solving these problems lies in breaking them down step by step and carefully identifying the information provided and the question being asked.
Steps to Solve Word Problems
Here is a simple approach to effectively tackle word problems:
- Read the problem carefully – Make sure to read through the entire problem to understand the context and the information given.
- Highlight important details – Identify key numbers, units, and operations required.
- Choose the right operation – Decide whether to add, subtract, multiply, or divide based on the problem’s requirements.
- Set up an equation – If necessary, translate the word problem into a mathematical equation to make it easier to solve.
- Check your work – After solving the problem, reread the question and ensure that your solution makes sense in the context of the problem.
Common Mistakes and How to Avoid Them
- Overlooking units: Ensure that all units (e.g., inches, dollars, minutes) are correctly noted and carried through the calculation.
- Misinterpreting the question: Pay attention to whether the problem asks for a total, a difference, or a specific number of items to be solved for.
- Skipping steps: Word problems often involve multiple steps. Don’t rush through them–take the time to work through each part systematically.
By following these steps and practicing regularly, students can improve their ability to solve word problems and apply mathematical reasoning in real-world situations.
Strategies for Solving Fractions and Decimals

Understanding and solving problems involving fractions and decimals is a crucial skill in this section. These concepts are often interconnected, and mastering them requires a combination of strategies that ensure accuracy in calculations. By applying the right methods, students can simplify problems and arrive at correct solutions more confidently.
Approaches for Working with Fractions
Here are some key strategies for simplifying and solving fraction problems:
- Find common denominators: When adding or subtracting fractions, it’s essential to find a common denominator before performing the operation.
- Simplify fractions: Always simplify fractions to their lowest terms by dividing both the numerator and denominator by their greatest common divisor.
- Convert improper fractions: If dealing with improper fractions, convert them into mixed numbers to make calculations easier and more intuitive.
Approaches for Working with Decimals
Decimals present their own set of challenges, but with the following strategies, they become more manageable:
- Align decimal points: When adding or subtracting decimals, always ensure that the decimal points are aligned vertically.
- Convert decimals to fractions: In some cases, it’s easier to work with fractions. Converting decimals to fractions can make operations simpler, especially in addition or subtraction.
- Round decimals: For complex decimal calculations, rounding the numbers to a manageable number of decimal places can help simplify the process.
By practicing these techniques regularly, students will build a stronger foundation for working with both fractions and decimals, ultimately improving their problem-solving skills.
Importance of Reviewing Each Response
Reviewing each solution carefully is a critical step in ensuring accuracy and understanding. Many students may rush through tasks, especially when they feel confident about their initial answers. However, taking the time to double-check every step and final result can prevent small mistakes from going unnoticed and can improve overall performance in solving problems.
Benefits of a Thorough Review
There are several key reasons why reviewing solutions is essential:
- Spotting errors: A second look often reveals simple mistakes such as miscalculations, incorrect signs, or overlooked steps that can change the outcome.
- Ensuring clarity: Revisiting each step helps verify that the correct method was used and that the reasoning behind each answer is sound.
- Improving comprehension: Reviewing reinforces understanding by allowing students to reflect on the concepts applied in solving the problem.
Effective Strategies for Review
Here are a few strategies for reviewing answers effectively:
- Work backward: Start from the final result and check if the steps logically lead to that conclusion.
- Compare with similar problems: Review similar exercises to ensure consistency in solving methods and answers.
- Use estimation: Before finalizing answers, quickly estimate the result to see if the final solution makes sense.
By adopting these review practices, students can minimize errors, boost their confidence, and enhance their overall problem-solving abilities.
Tips for Improving Problem-Solving Skills
Enhancing problem-solving abilities is a key part of mastering any subject that requires logical reasoning and critical thinking. The ability to approach challenges methodically, break down complex tasks, and apply strategies effectively is essential for success. By practicing the right techniques, students can sharpen their skills and become more confident in their approach to solving problems.
Effective Strategies for Problem Solving
Here are several tips that can help improve problem-solving skills:
- Understand the problem: Before jumping into calculations, take the time to thoroughly read the problem and identify what is being asked. Clarify any unfamiliar terms or concepts.
- Break it down: Divide the problem into smaller, more manageable parts. Solving simpler steps one at a time often leads to a clearer solution.
- Stay organized: Keep work neat and follow a systematic approach. Write down important information, draw diagrams if needed, and label each step clearly.
- Use estimation: Before solving, make an educated guess about the answer. Estimation helps set expectations and can guide the solving process.
- Check your work: After reaching a solution, review each step to ensure no mistakes were made. Double-checking can help catch errors before finalizing answers.
Building Problem-Solving Confidence
Regular practice is key to improving problem-solving skills. Here are some tips to build confidence:
- Practice regularly: Consistent practice reinforces concepts and helps internalize methods. Try solving a variety of problems to gain exposure to different types of challenges.
- Learn from mistakes: Mistakes are a valuable learning opportunity. Analyze where things went wrong and adjust your approach for future problems.
- Ask for help: If you’re stuck, don’t hesitate to seek guidance. Discussing a problem with a peer or teacher can provide new insights and alternative methods.
By implementing these strategies and maintaining a positive, persistent mindset, students can significantly enhance their ability to solve problems efficiently and accurately.
How to Check Your Responses Correctly

Reviewing your work is an essential step in ensuring accuracy. Often, minor mistakes can be overlooked during the first attempt, but taking the time to double-check each response can help identify errors and improve overall performance. By following a systematic approach, you can verify your solutions with confidence and reduce the chances of making careless mistakes.
Steps for a Thorough Review
Here are some key strategies for reviewing your work effectively:
- Go step-by-step: Revisit each step of the process to ensure that you followed the correct procedure. Check if you applied the right formulas or methods for each task.
- Look for common errors: Watch for common mistakes such as miscalculating numbers, switching operations, or forgetting to simplify fractions or decimals.
- Estimate the result: Before finalizing your solution, quickly estimate what the result should be. If the final answer seems unrealistic compared to your estimate, recheck your steps.
- Compare with similar problems: Look at similar exercises you have completed and compare the methods used to solve them. This can help ensure consistency in your approach.
Using a Checklist for Accuracy
Creating a checklist can be a helpful tool when verifying your responses. Below is an example of how to structure your review process:
| Step | Action | Check |
|---|---|---|
| Step 1 | Review the initial problem and identify the task. | Ensure all aspects of the question are understood. |
| Step 2 | Recheck your calculations and steps. | Confirm no arithmetic mistakes were made. |
| Step 3 | Compare your solution to estimates or benchmarks. | Ensure the answer is reasonable and matches expectations. |
| Step 4 | Double-check any written explanations or reasoning. | Ensure clarity and accuracy in the thought process. |
By following these steps and utilizing checklists, you can significantly improve your ability to verify responses and increase the accuracy of your work.
Engaging with Interactive Practice Exercises
Interactive exercises provide an effective way to reinforce concepts and solidify understanding. By engaging with hands-on activities, learners can actively apply what they have learned, which enhances retention and problem-solving skills. These exercises offer a dynamic approach to learning, as they allow individuals to experiment with different strategies and receive immediate feedback on their progress.
Using interactive tasks is beneficial for identifying areas where more practice is needed and for gaining a deeper understanding of the material. The ability to work through problems in real-time promotes confidence and ensures that learners can tackle various challenges on their own. Whether it’s through digital platforms or physical worksheets, interactive practice offers endless opportunities for improvement.
By making learning more engaging and enjoyable, interactive exercises encourage a more proactive approach to mastering the material, making it easier to overcome obstacles and build a strong foundation for future topics.
Support Resources for Grade 5 Math
Having access to quality support resources can significantly enhance a learner’s ability to understand complex concepts. These materials provide extra practice, clarify difficult topics, and offer strategies for tackling challenging problems. Whether through online tools, study guides, or personalized tutoring, support resources offer essential help to students who want to improve their skills and confidence.
Teachers, parents, and online platforms all contribute to creating a supportive learning environment. With a range of resources available, students can find materials that match their individual learning style, whether visual, auditory, or hands-on. Support resources make it possible for learners to receive guidance when needed and practice at their own pace to master key concepts.
Online Learning Platforms

Online platforms provide a wealth of interactive lessons, quizzes, and instructional videos that cater to different learning needs. These resources allow students to work at their own pace and receive immediate feedback on their performance. By using online tools, learners can access a variety of explanations and approaches to help them overcome specific challenges.
Study Guides and Practice Sheets
Printed or digital study guides offer clear and structured explanations of core concepts. Practice sheets, filled with problems and solutions, allow students to apply what they’ve learned and reinforce their understanding. These resources are ideal for review and self-assessment, helping students identify areas that need more attention before moving on to more advanced topics.
Building Confidence in Math with Module 2
Gaining confidence in solving mathematical problems is a crucial step for students in their educational journey. By mastering foundational concepts, learners not only strengthen their problem-solving skills but also develop a positive attitude toward tackling more challenging tasks. Consistent practice, clear explanations, and step-by-step guidance are essential in helping students feel more comfortable with complex topics.
The second unit of this learning series is designed to reinforce key skills and build a sense of achievement. By completing exercises and reviewing core concepts, students can gradually overcome their fears and doubts about their abilities. With time and focused effort, learners gain the confidence they need to approach math problems with a positive mindset.
Steps to Build Confidence
- Start with simpler problems to gradually build up understanding.
- Use visuals and examples to connect concepts with real-life situations.
- Encourage consistent practice and reviewing mistakes as opportunities to improve.
- Break down larger problems into smaller, more manageable parts.
Supportive Learning Techniques
- Interactive exercises that offer instant feedback help students learn from mistakes.
- Peer collaboration allows students to share solutions and learn from one another.
- Regular progress tracking and celebrating small victories keep learners motivated.
How Module 2 Prepares for Future Math Topics

The second unit in this learning series serves as a critical foundation for understanding more advanced topics that students will encounter in the future. By focusing on essential principles and providing opportunities for practice, this section ensures that learners develop the necessary skills to tackle increasingly complex concepts. Building a strong base in these areas helps students transition smoothly to more sophisticated mathematical challenges.
In particular, the lessons focus on problem-solving strategies, enhancing students’ abilities to break down and approach new topics in a structured way. These skills are not only applicable in subsequent lessons but also crucial for understanding higher-level concepts in later stages of learning. By mastering the core skills in this section, learners position themselves for success in the future, as they will encounter these foundational ideas repeatedly in more advanced studies.
Key Areas Covered in Module 2
| Topic | Skills Developed | Future Application |
|---|---|---|
| Fractions and Decimals | Understanding operations with fractions and decimals | Used in algebra and real-world problem solving |
| Word Problems | Breaking down complex problems into simpler steps | Essential for higher-level problem-solving and equations |
| Measurement | Applying measurement concepts to various scenarios | Foundational for geometry and scientific calculations |
Connecting to Future Topics
Once these concepts are mastered, students will find it easier to tackle subjects such as algebra, geometry, and data analysis. The skills developed in this section lay the groundwork for understanding equations, ratios, and proportions in future lessons. Each concept builds on the previous one, ensuring that learners are well-prepared for the challenges ahead. With a strong grasp of the foundational material, students can approach more advanced topics with confidence and readiness.
Using the Answer Key for Self-Assessment
Self-assessment is an essential part of the learning process, as it allows students to evaluate their understanding and identify areas for improvement. By comparing their solutions to the provided reference, learners can check their progress, verify their methods, and ensure that they grasp key concepts. This approach fosters independent learning and encourages students to take responsibility for their own education.
When using a reference to check work, it’s important to go beyond simply confirming correct answers. Students should reflect on how they arrived at each solution, consider alternative approaches, and pinpoint any mistakes made along the way. This process helps solidify understanding and enhances problem-solving skills. Over time, learners can track their progress and see how their abilities improve with consistent practice.
Benefits of Consistent Practice and Review

Regular practice and review play a crucial role in mastering any subject. By revisiting concepts and solving problems repeatedly, students reinforce their understanding and develop greater proficiency. This approach not only helps in retaining information but also boosts confidence and builds a strong foundation for more complex topics.
Consistent engagement with the material ensures that learners stay familiar with the content, making it easier to recall when needed. Reviewing past work also helps identify areas of difficulty early on, allowing students to address these challenges before they become bigger obstacles. This habit promotes active learning and a deeper understanding of the concepts at hand.
Key Advantages of Regular Practice
- Improved Retention: Repeated exposure to concepts makes them more memorable and easier to recall.
- Increased Speed: Practice helps to solve problems more quickly and efficiently over time.
- Stronger Problem-Solving Skills: Regular practice sharpens critical thinking and decision-making abilities.
How Review Enhances Learning
- Identifying Weak Areas: Revisiting past material highlights areas that need more attention.
- Building Confidence: Successfully solving problems after review reinforces self-assurance.
- Filling Knowledge Gaps: Reviewing ensures no concepts are left misunderstood or forgotten.