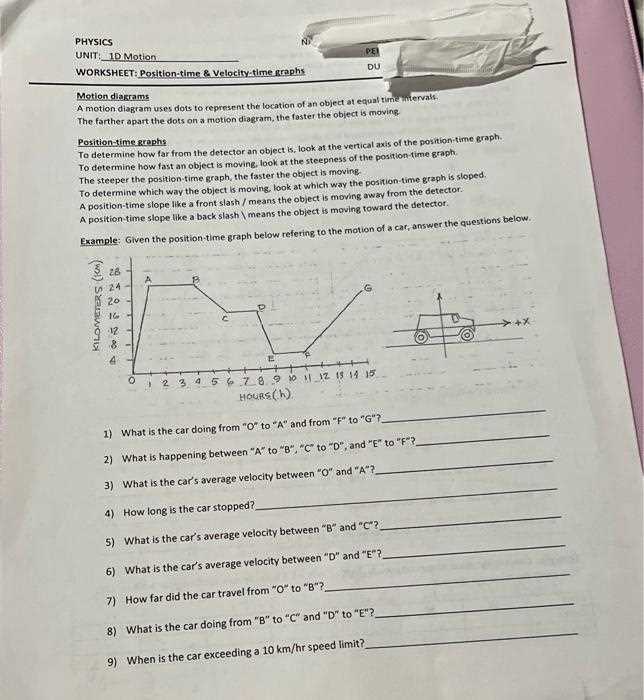
In physics, visual representations are often used to convey complex motion patterns. These charts help in understanding how an object moves over a certain period, illustrating key changes and trends. By analyzing such visuals, one can uncover detailed insights into the speed and behavior of an object throughout its journey.
Grasping the concept of these visual aids is essential for solving related exercises. They offer a systematic approach to breaking down the object’s progress, helping to identify patterns such as acceleration, deceleration, and uniform motion. The ability to interpret such diagrams correctly enhances comprehension and problem-solving skills in motion studies.
Practical exercises based on these representations challenge learners to apply theoretical knowledge and improve their analytical abilities. With the right approach, solving such problems becomes an engaging process that strengthens one’s understanding of the subject.
Velocity Time Graphs Worksheet Answers
When analyzing motion through visual representations, interpreting data correctly is crucial for understanding an object’s behavior over a specific duration. These exercises require the ability to break down various components of motion and make sense of the patterns shown. The process involves extracting valuable information from these diagrams, which can then be used to solve related questions and scenarios effectively.
Key Concepts to Master
- Understanding acceleration and its representation
- Identifying uniform motion versus changing speed
- Determining the area under the curve for distance
- Recognizing zero movement and its significance
- Interpreting slopes to calculate rate of change
Steps for Solving Problems
- Examine the diagram and identify key features.
- Analyze each section for acceleration or constant speed.
- Calculate relevant quantities such as distance or rate of change.
- Interpret the results and check for consistency in the context of the problem.
By following these steps and understanding the principles behind them, solving motion-related problems becomes a straightforward task. This approach ensures that learners can approach any given challenge with confidence and accuracy, enhancing their comprehension of motion dynamics.
Understanding the Basics of Motion Diagrams
In motion analysis, understanding how to interpret visual charts is key to grasping the movement of objects. These charts are designed to show changes in an object’s speed over a period. By reading and analyzing them, you can uncover vital information, such as whether an object is accelerating, decelerating, or maintaining a steady pace.
Key Features of Motion Diagrams
- Horizontal lines indicating constant speed
- Sloped lines representing acceleration or deceleration
- Curved lines showing varying rates of change
- Areas under the curve corresponding to distance traveled
How to Interpret These Diagrams
When analyzing such diagrams, it is essential to focus on the slope and shape of the curve. A steeper slope usually indicates a greater rate of change in speed, while a horizontal line shows uniform motion. By understanding these basic principles, you can easily break down complex motion scenarios and apply the correct equations to solve them.
How to Read a Motion Diagram
Interpreting motion charts requires a clear understanding of how the visual elements represent the changes in an object’s movement. These diagrams are designed to show how speed evolves over a certain period, allowing you to extract valuable details such as acceleration, deceleration, or constant motion. By learning to read the chart accurately, you can identify the key phases of movement and calculate various aspects of the object’s travel.
Identifying Key Elements
- The slope of the line: steeper slopes represent higher acceleration or deceleration.
- Flat sections: indicate periods of constant speed.
- Positive and negative regions: show forward and backward motion respectively.
- Area under the curve: helps calculate the distance traveled.
Steps for Reading a Diagram
Start by examining the overall shape of the line. If the line rises, the object is speeding up; if it falls, it is slowing down. A flat line means the object is moving at a constant rate. Pay attention to the magnitude of the slope to understand the rate of change. Lastly, focus on the areas between the curve and the axis to determine how far the object has traveled during each phase of motion.
Interpreting Slopes in Motion Diagrams
Understanding the slope of a line in motion diagrams is crucial for analyzing an object’s behavior. The steepness and direction of the slope provide valuable insights into the rate at which the object’s speed is changing. By carefully examining these slopes, you can determine whether the object is accelerating, decelerating, or maintaining a constant rate of movement.
Types of Slopes and Their Meaning
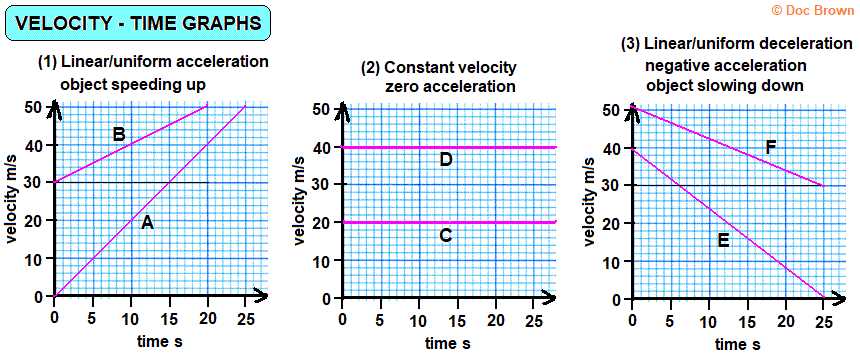
- Positive slope: indicates increasing speed, or acceleration.
- Negative slope: shows a decrease in speed, or deceleration.
- Zero slope: represents constant motion, where the object’s speed remains unchanged.
- Steep slope: indicates a high rate of change in speed.
- Shallow slope: suggests a low rate of change in speed.
How to Analyze Slopes Effectively

- Examine the steepness: a steeper slope means a faster change in speed.
- Consider the direction: an upward slope means increasing speed, while a downward slope indicates slowing down.
- Look for flat sections: these represent periods of uniform motion where the speed remains constant.
By mastering the interpretation of slopes, you can gain a deeper understanding of the object’s motion, making it easier to solve related problems and predict its future behavior.
Calculating Speed from Motion Diagrams
Determining an object’s speed from a motion diagram involves analyzing the slope and shape of the line. The slope provides essential information about how the speed changes over time, and by applying the right calculations, you can determine the exact speed at any given point. This process requires a strong understanding of the relationship between the variables represented in the diagram and the underlying equations of motion.
Step-by-Step Process for Calculation
- Identify the relevant section of the diagram where the speed is either constant or changing.
- For a linear section, calculate the slope to determine the rate of change in speed.
- If the line is flat, the speed is constant, and no calculation is needed for that period.
- For curves, estimate the average rate of change over a small interval and use it to calculate the instantaneous speed.
Using the Slope to Calculate Speed
For sections where the line is straight, the slope can be used directly to calculate the change in speed. The formula for slope is the change in vertical value (speed) divided by the change in horizontal value (time). In cases of non-linear sections, breaking the curve into smaller straight segments allows for approximate calculations. These methods give an accurate representation of the object’s motion and can be applied to various types of diagrams.
Common Mistakes in Motion Diagrams
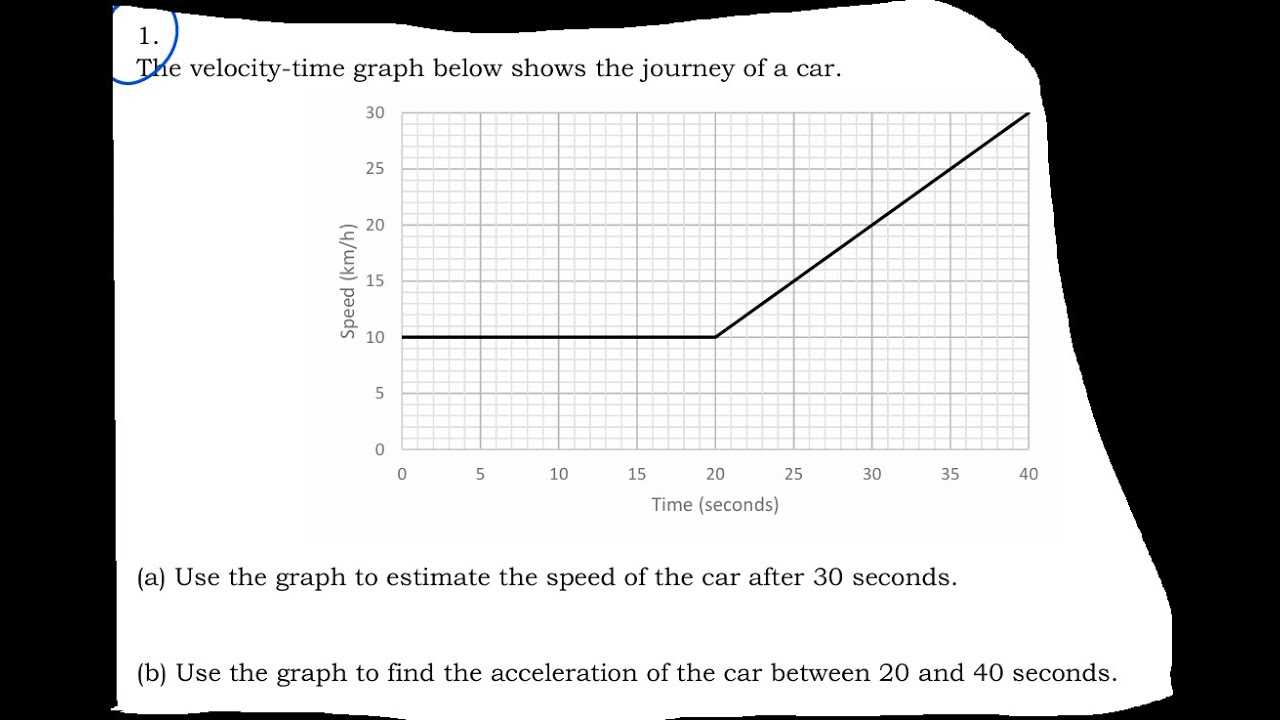
When analyzing motion through visual diagrams, it’s easy to make errors in interpretation. These mistakes often arise from misunderstanding the relationship between the graph’s components, misreading the scale, or overlooking key details that influence the object’s movement. Being aware of these common pitfalls helps avoid confusion and ensures more accurate analysis.
Typical Errors in Motion Analysis
| Error | Description | Solution |
|---|---|---|
| Incorrectly interpreting slopes | Assuming the slope is constant when it changes, leading to wrong conclusions about acceleration. | Always check the slope carefully and note if it changes, indicating varying acceleration. |
| Misunderstanding flat sections | Assuming the object is at rest during flat sections, when it may be moving at a constant speed. | Recognize that flat lines indicate uniform motion, not a lack of movement. |
| Overlooking negative areas | Failing to account for the area beneath negative sections, which represent distance traveled in the opposite direction. | Ensure that all areas, including those below the axis, are considered for total displacement. |
| Not factoring in units | Forgetting to use consistent units when calculating quantities like speed or distance. | Always double-check units and convert them when necessary to maintain consistency throughout calculations. |
By avoiding these common mistakes, you can more effectively interpret motion diagrams and gain a clearer understanding of an object’s behavior over time. Being mindful of these details ensures that calculations and conclusions are accurate, helping to build a stronger grasp of motion analysis concepts.
Understanding Acceleration on Motion Diagrams
Acceleration is a key aspect of motion analysis, reflecting how an object’s speed changes over a period. On visual representations of motion, acceleration is often shown through the slope of the curve. The steeper the slope, the greater the rate of acceleration, while a horizontal line indicates no change in speed. Understanding these patterns allows for accurate interpretation and calculation of acceleration in various scenarios.
How to Identify Acceleration
| Slope Type | Interpretation | Acceleration |
|---|---|---|
| Positive slope | Object’s speed is increasing | Positive acceleration (speeding up) |
| Negative slope | Object’s speed is decreasing | Negative acceleration (slowing down) |
| Zero slope | Object is moving at a constant speed | No acceleration |
Calculating Acceleration from the Slope
To calculate acceleration, simply find the slope of the line within a given section of the diagram. The formula for the slope is the change in vertical position (speed) divided by the change in horizontal position (time). A steeper slope indicates a higher rate of acceleration, while a shallower slope suggests a slower change in speed. For non-linear curves, the acceleration can vary, requiring calculations for specific intervals.
How to Find Distance from Motion Diagrams
Determining the total distance traveled from a motion diagram involves calculating the area under the curve. The distance represents the object’s path, and in some cases, this can be split into different segments based on the diagram’s shape. Understanding how to interpret these areas allows you to accurately calculate the distance, whether the motion is uniform or changing.
Methods for Calculating Distance
- For constant speed: The area under a flat line represents the total distance, which can be calculated as speed multiplied by time.
- For accelerating or decelerating motion: The area under the curve can be broken into simpler shapes like triangles or rectangles, which can then be calculated and summed.
- For curved lines: Approximate the area by dividing the curve into smaller segments, calculate the area of each segment, and then add them together for an estimate of the total distance.
Calculating Area for Different Shapes

- Rectangles: Area = width × height (time × speed).
- Triangles: Area = 0.5 × base × height (0.5 × time × change in speed).
- Trapezoids: Area = 0.5 × (base1 + base2) × height (0.5 × (initial speed + final speed) × time).
By applying these techniques, you can accurately calculate the total distance an object has traveled during different phases of its motion, even when the motion is not uniform. This method of analysis is essential for solving problems involving displacement and distance in various contexts.
What Does the Area Represent?
The area beneath a curve in a motion diagram provides important information about the object’s movement over a period. In many cases, this area correlates directly with key physical quantities, such as distance traveled or change in velocity. By analyzing the space under the curve, you can derive valuable insights into the motion’s characteristics and behavior.
Understanding the Significance of the Area
- Distance traveled: The area under the curve represents the total distance an object has moved. This applies to both constant and changing speeds.
- Displacement: In some cases, the area can also indicate displacement, taking into account the direction of motion, especially when there are negative areas (below the axis).
- Impulse: In certain contexts, the area under the curve represents the total impulse applied to an object, particularly when analyzing force and momentum.
- Change in momentum: For non-uniform motion, the area under the curve can reflect the change in momentum, helping to understand how the object’s motion is influenced by external forces.
How to Interpret Area in Different Scenarios
- For uniform motion, the area is typically a rectangle, and the calculation is straightforward: speed × time.
- For accelerating or decelerating motion, the area may form a triangle or trapezoid, requiring the application of basic geometric formulas to find the total distance or change in momentum.
- For non-linear motion, approximate methods like numerical integration can be used to estimate the area under the curve.
By analyzing the area under the curve, you can gain a deeper understanding of the object’s motion and apply this knowledge to solve complex problems related to speed, displacement, and momentum.
Key Features of Motion Diagrams
When analyzing the motion of an object, certain characteristics stand out, which can be easily observed from the visual representation of the object’s movement. These features offer critical insights into how the object behaves during its motion, including changes in speed, direction, and acceleration. Understanding these key elements helps in interpreting the overall dynamics of the system.
One of the most important aspects of these diagrams is the shape and slope of the curve. The curve’s direction and steepness provide information about whether the object is speeding up, slowing down, or moving at a constant rate. The area under the curve also plays a significant role, as it can represent the total distance traveled or other physical quantities, depending on the context.
Another crucial element is the intersection with the axis, which often indicates important changes in motion. For example, crossing the horizontal axis can signal a change in direction, while a flat line (horizontal segment) shows that the object is moving at a constant speed or is at rest.
Identifying Uniform Motion in Diagrams
Uniform motion refers to movement where an object maintains a constant speed over a specific period. Recognizing this pattern in a motion diagram is essential for understanding the object’s behavior. When analyzing such a diagram, the key indicator of uniform motion is a straight, horizontal line, showing that the object is moving without any acceleration or deceleration.
Features of Uniform Motion
- Horizontal Line: A straight, flat line indicates that the object’s speed remains unchanged during the period being analyzed.
- Constant Area: The area under the curve is consistent, representing a steady rate of displacement over time.
- No Curvature: Unlike non-uniform motion, uniform movement does not exhibit any curves or changes in slope.
How to Recognize Uniform Motion
To identify uniform motion in a diagram, look for a section where the line remains at a consistent height above the horizontal axis, indicating a constant rate of motion. In contrast to fluctuating or curved lines, the absence of slope changes confirms that the object is not accelerating or decelerating, but rather maintaining a steady pace throughout.
How to Handle Non-linear Diagrams
When dealing with motion that changes at an uneven rate, the diagram representing this movement often takes on a curved shape. These types of diagrams can be more complex than linear ones, but they provide valuable information about how the object’s speed and direction evolve over time. Understanding how to interpret these curves is crucial for analyzing non-uniform motion.
Recognizing Non-linear Movement
- Curved Line: Unlike straight lines, a curve indicates that the object is either speeding up or slowing down. The steeper the curve, the greater the change in speed.
- Changing Slope: In non-linear motion, the slope of the curve continually changes. This reflects the varying acceleration of the object.
- Uneven Areas: The area under the curve in non-linear diagrams will vary depending on the shape of the curve. Different methods, such as numerical integration, are used to calculate these areas.
Interpreting Curves and Their Implications
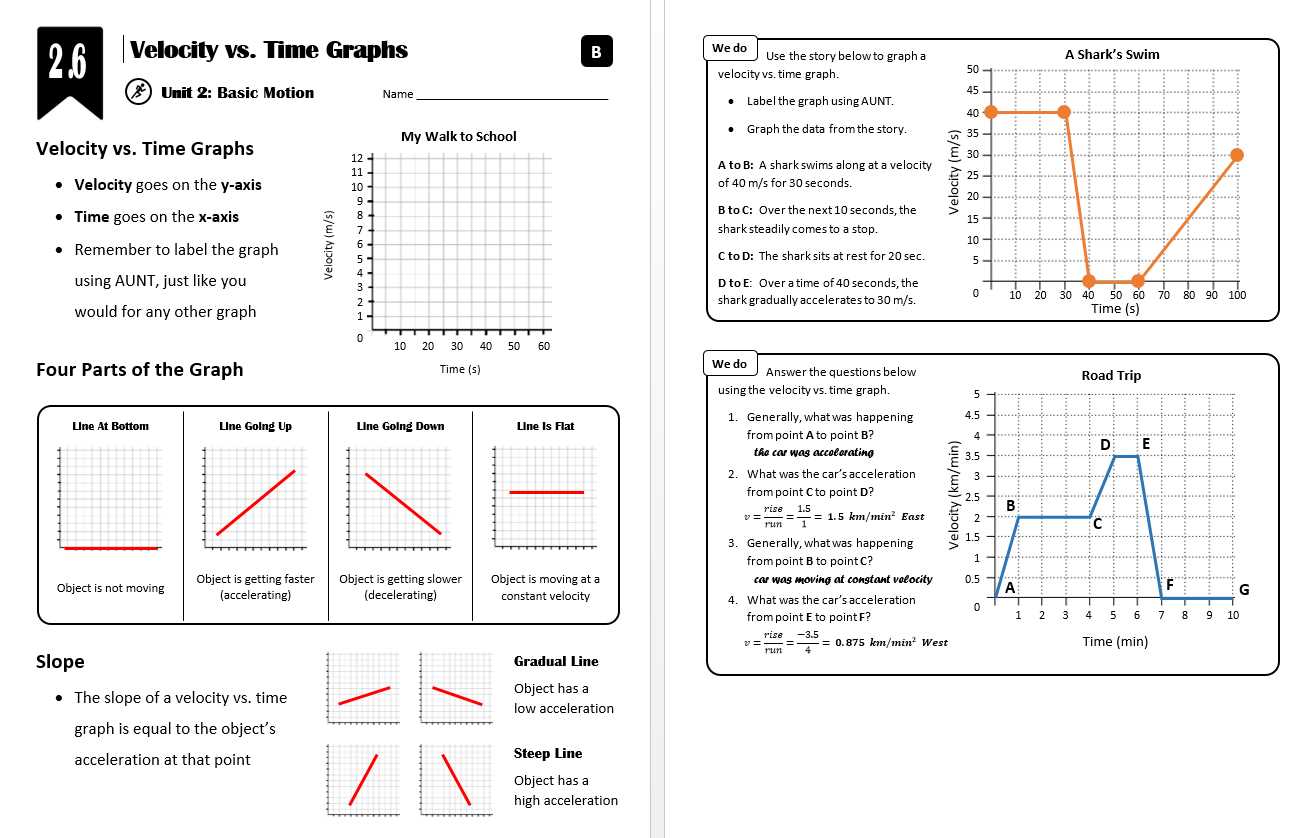
To effectively analyze non-linear motion, observe the curvature and its direction. A concave curve suggests increasing speed (acceleration), while a convex curve may indicate decreasing speed (deceleration). By closely examining the curve’s shape, it becomes possible to estimate the changes in speed and make informed predictions about the object’s future motion.
Interpreting Changes in Speed
Changes in speed are fundamental to understanding how an object behaves as it moves. These shifts can indicate acceleration, deceleration, or even a complete stop. By analyzing how an object’s motion changes over a specific period, we can determine whether it is speeding up, slowing down, or maintaining a steady pace. Recognizing these variations is essential for predicting future movement and understanding the forces at play.
When examining a motion diagram, it is important to focus on the slope and direction of the line. A rising line typically signals an increase in speed, while a falling line suggests a decrease. A horizontal line, on the other hand, shows constant speed. By noting how the graph transitions, one can interpret whether the object is accelerating or decelerating at any given point.
Velocity Diagrams in Real-World Scenarios
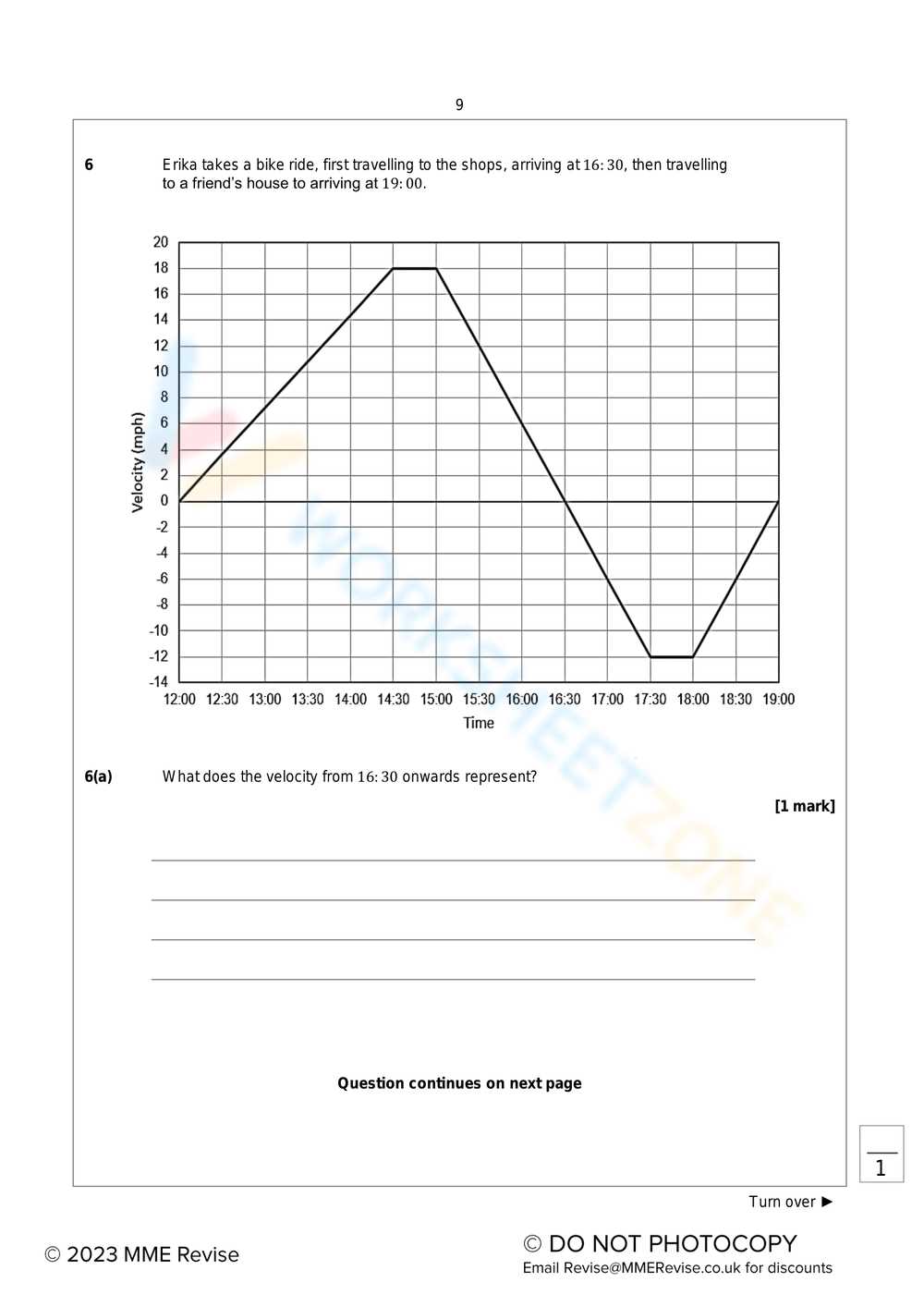
Understanding how objects move in the real world often involves analyzing their motion using various diagrams. These visual tools provide insights into how an object’s speed changes in different situations, from vehicles on a road to athletes in motion. Real-world applications help us interpret complex movement patterns, predict behavior, and optimize performance.
In everyday life, motion analysis is used in various fields. For instance, car manufacturers rely on motion diagrams to study how vehicles accelerate, decelerate, and maintain speed during different driving conditions. Similarly, athletes and coaches use these tools to monitor the speed variations during training or competitions, optimizing their strategies for better performance.
Analyzing Motion with Negative Speed
When analyzing motion, encountering negative values can often be interpreted as a change in direction. Negative speed indicates that an object is moving in the opposite direction relative to its initial movement. Understanding how to interpret these negative values is essential for accurately analyzing complex motion scenarios where an object may reverse course or move backward.
In practical terms, a negative value typically signifies a reversal in movement, such as when a car moves in reverse or when an object accelerates in the opposite direction. This concept is important in various real-world applications, such as physics experiments, traffic studies, and sports analytics, where the direction of movement is just as critical as the speed itself.
Understanding Graphs with Zero Speed
In motion analysis, encountering a flat line often signals a period of rest or constant position. When an object’s speed is zero, it indicates that there is no movement at that specific moment in time. Understanding this scenario is crucial for interpreting situations where an object is stationary or not changing its location, even though time is still passing.
A zero-speed scenario can occur in various situations. For example, a car at a red light, a person standing still, or an object resting on a surface all exhibit no movement. Zero speed does not mean the object is not experiencing forces; rather, it simply implies there is no displacement over time. Recognizing these periods of stillness can help in understanding the complete motion profile of an object.
Tips for Solving Worksheet Problems
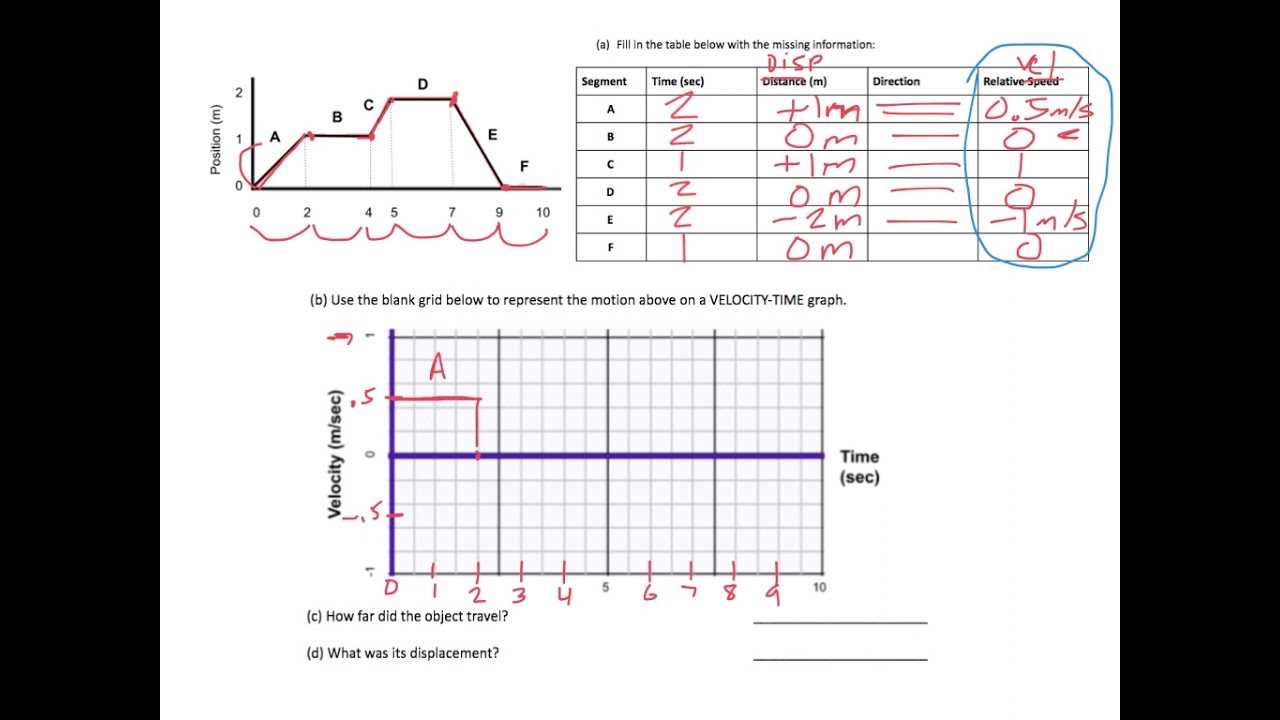
When tackling exercises related to motion analysis, it’s essential to approach each problem methodically to ensure accurate results. By breaking down each task step-by-step, you can better understand how different elements of motion interact. Whether you’re analyzing speed, distance, or acceleration, following a structured process can help simplify complex scenarios.
1. Understand the Problem
Before starting any calculations, make sure you fully understand what is being asked. Read the problem carefully and identify key information such as initial conditions, any changes in motion, and what you need to find. This will help guide your approach and ensure you don’t overlook important details.
2. Break It Down into Steps
Once you have a clear understanding, break the problem into smaller steps. If the problem involves interpreting a chart or calculating specific values, focus on one part at a time. For instance, first identify the relevant intervals, then determine the necessary formulas or methods to apply.
Tip: Visualize the motion by sketching a diagram or marking key points on a graph. This will provide a clearer picture and help you avoid errors in interpretation.
3. Double-Check Your Units
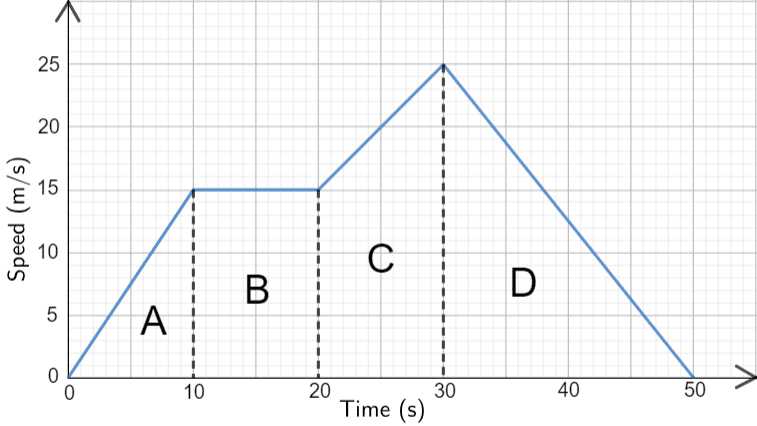
Always make sure your units are consistent throughout the calculations. Converting units when necessary can prevent mistakes that arise from mismatched measurements. This is especially important when working with quantities like distance and speed, as mixing units can lead to incorrect results.
By following these tips, you can approach each problem with confidence and ensure accurate interpretations of the motion under analysis.