
Mathematics often presents us with challenges that require creative thinking and logical reasoning. In this segment, we delve into a collection of exercises designed to enhance analytical skills and promote a deeper understanding of various mathematical principles. These activities serve as a bridge between theoretical concepts and practical application, fostering confidence in problem-solving.
The focus of this section is to guide learners through intricate scenarios that test their ability to identify patterns, apply formulas, and think critically. By examining a variety of tasks, participants gain exposure to diverse methods and strategies, equipping them with the tools to approach similar problems in the future with clarity and precision.
Here, you will find detailed insights and explanations to help unravel the complexities of each task. This comprehensive approach not only aids in mastering specific techniques but also reinforces the foundational skills essential for tackling broader mathematical topics.
Chapter 6 Geometry Worksheet Answers
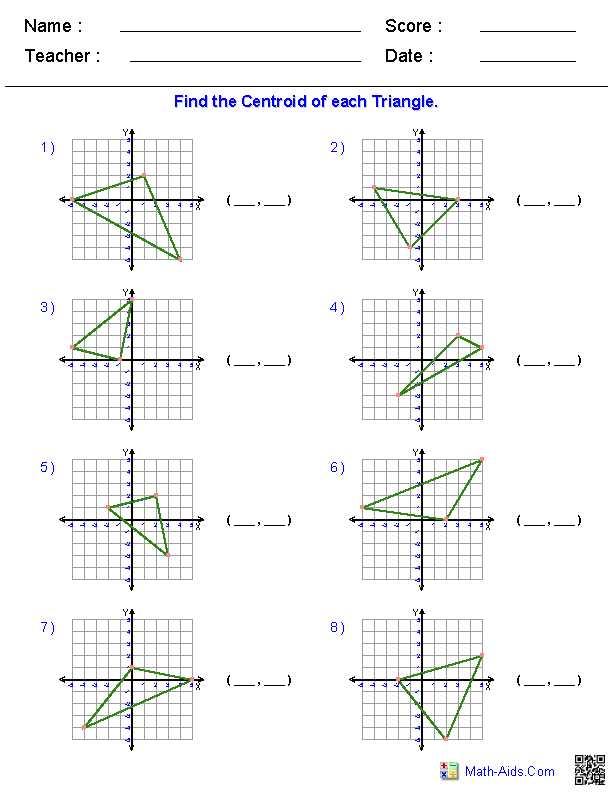
This section provides a structured approach to tackling complex mathematical challenges related to spatial reasoning and shapes. By reviewing the concepts and methods outlined here, learners can enhance their ability to interpret diagrams, apply formulas, and solve intricate problems with confidence.
- Key Concepts: An overview of essential principles, including relationships between angles, properties of various forms, and methods for calculating areas and perimeters.
- Step-by-Step Solutions: Detailed explanations for each exercise, ensuring a clear understanding of the logic and computations involved.
- Practical Applications: Examples that connect theoretical knowledge with real-world scenarios, emphasizing the importance of accurate analysis.
- Common Mistakes: Insights into frequent errors and tips for avoiding them to improve problem-solving efficiency.
Understanding Key Geometry Concepts
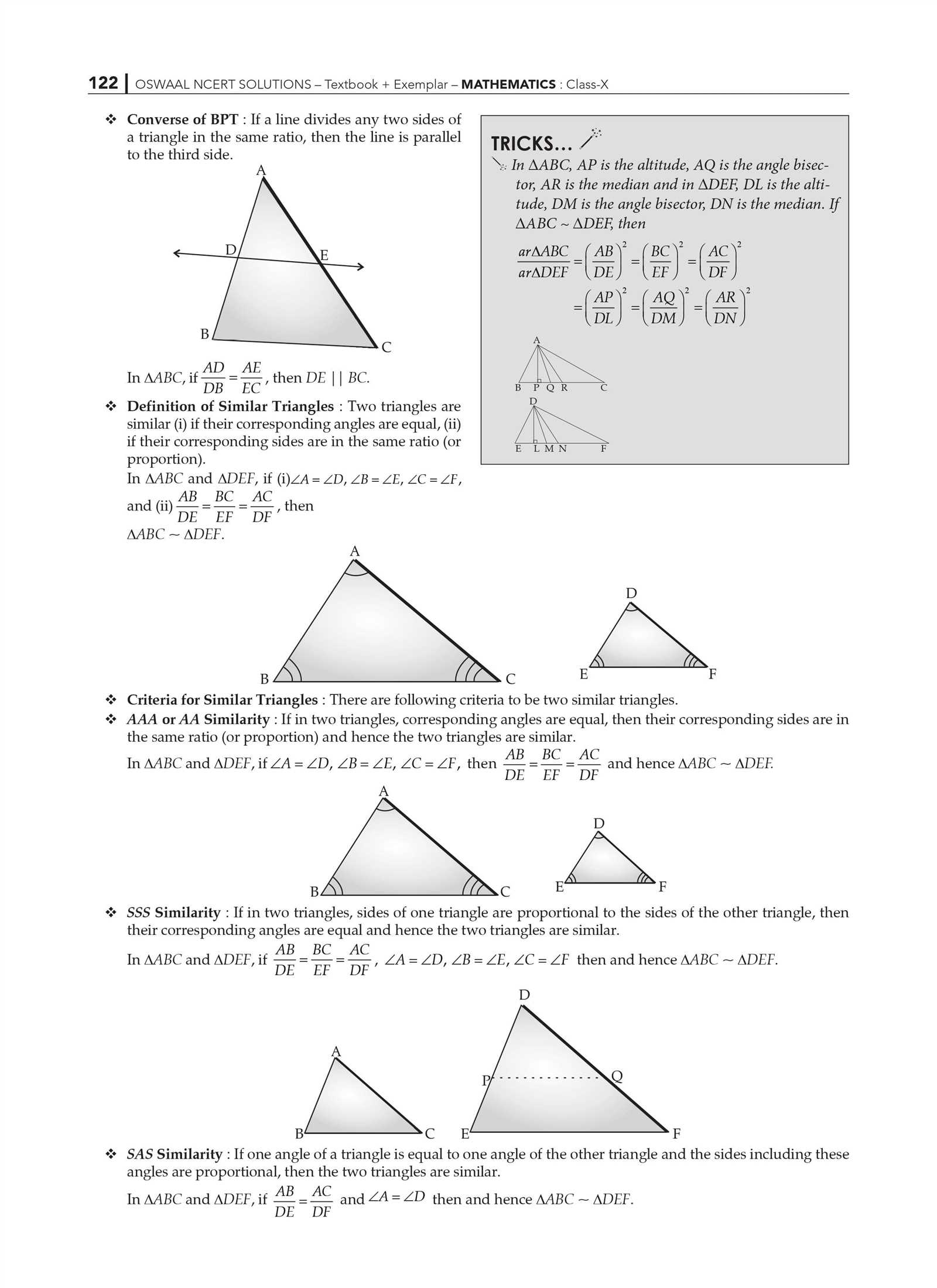
Mathematical reasoning often involves interpreting shapes, understanding relationships, and applying logical steps to solve problems. This section focuses on core ideas that form the basis of spatial calculations and their practical applications. These principles are essential for analyzing forms and creating accurate solutions in various contexts.
Key elements include identifying relationships within structures, such as angles, sides, and points, and utilizing established rules to calculate dimensions or verify symmetry. Exploring these ideas helps develop a solid foundation for solving more advanced problems efficiently and accurately.
By mastering these fundamental concepts, learners gain the tools to approach tasks with clarity and confidence, ensuring a deeper comprehension of spatial reasoning and its role in mathematical problem-solving.
Step-by-Step Guide to Solutions
Breaking down complex problems into manageable steps is a reliable method for achieving accurate results. This section offers a detailed walkthrough of various exercises, focusing on logical reasoning and the application of mathematical principles. Each process is designed to clarify the problem-solving approach and strengthen understanding.
Analyzing the Problem
The first step in solving any task is to carefully examine the given information. Identify key elements, such as measurements, relationships, or specific patterns. Understanding these details lays the foundation for effective problem-solving and ensures no critical aspect is overlooked.
Applying Formulas and Techniques
Once the problem is clearly defined, the next phase involves selecting and implementing the appropriate strategies. Whether it’s calculating dimensions, verifying properties, or determining relationships, this stage emphasizes precision and logical progression. Detailed calculations and checks ensure that the final results are both accurate and reliable.
By following this structured approach, learners can tackle even the most challenging tasks with confidence, enhancing their skills and preparing them for more advanced topics.
Common Mistakes in Geometry Worksheets
When solving mathematical problems related to shapes and space, errors often occur due to misinterpretation of the given information or incorrect application of principles. Recognizing these common pitfalls can help improve accuracy and avoid confusion. This section highlights typical mistakes that learners might encounter and offers tips for avoiding them.
Misunderstanding Measurements and Properties
A frequent mistake occurs when students misinterpret the dimensions or properties of shapes, such as mixing up the lengths of sides or incorrectly identifying angles. It’s essential to carefully examine the information and verify that all measurements are correctly understood before proceeding with calculations. Double-checking these details can prevent errors in subsequent steps.
Incorrect Formula Application
Another common error arises from applying the wrong formula or technique to solve a problem. Different shapes or scenarios require specific approaches, and failure to choose the appropriate one can lead to incorrect results. Ensure that the correct formula is selected based on the problem type, and remember to substitute values properly.
By being aware of these frequent mistakes and taking the time to carefully review each step, students can significantly reduce errors and improve their problem-solving skills.
How to Solve Geometry Word Problems
Solving word-based problems in mathematics requires the ability to translate real-world scenarios into mathematical terms. These problems often involve spatial reasoning and the application of specific principles to find unknown quantities. Approaching these tasks systematically helps break down complex situations into manageable steps.
Step 1: Read the Problem Carefully – The first step is to thoroughly understand the scenario presented. Identify key information such as shapes, measurements, and relationships. Pay attention to words that indicate mathematical operations, such as “sum,” “difference,” or “product.”
Step 2: Visualize the Situation – Drawing a diagram or sketching the described scenario is an excellent way to clarify the relationships between different elements. This visual representation can make it easier to see how various components interact and guide your next steps.
Step 3: Apply Relevant Principles – Use appropriate formulas or theorems based on the specific problem. Whether it involves calculating areas, finding angles, or working with properties of shapes, ensure that the right method is applied to the situation.
Step 4: Solve and Check – After performing the necessary calculations, review your results. Double-check that your answer aligns with the given information and makes sense in the context of the problem. If needed, revisit earlier steps to correct any potential errors.
By following this approach, learners can confidently tackle word-based problems and improve their problem-solving efficiency.
Visualizing Geometry Figures for Better Understanding
Being able to visualize mathematical shapes and their properties is a crucial skill for understanding and solving related problems. When we create a mental or physical image of a figure, we can better grasp the relationships between its parts, making it easier to apply mathematical concepts and principles. This section focuses on how visual representation enhances comprehension and problem-solving accuracy.
The Power of Drawing Diagrams
One of the most effective ways to understand a figure is to draw it. Sketching out the shape can reveal important details that might not be immediately obvious from the description alone. By labeling key elements such as lengths, angles, and intersections, students can see how different parts of the figure are connected, which aids in applying the right formulas and strategies.
Using Interactive Tools for Better Clarity
Modern technology offers various tools and software that allow for dynamic manipulation of figures. Interactive diagrams enable learners to rotate, zoom in, or adjust dimensions, giving them a deeper understanding of how changes affect the entire shape. These visual aids provide an immersive learning experience, making abstract concepts more tangible and easier to grasp.
By incorporating visual methods into problem-solving, learners can strengthen their spatial reasoning and tackle mathematical challenges with greater ease and precision.
Tips for Mastering Geometry Formulas
Mastering mathematical equations related to shapes and their properties is essential for solving a wide range of problems. These formulas provide the foundation for calculating dimensions, areas, and other key measurements. By understanding how and when to apply them, learners can improve their problem-solving efficiency and accuracy.
Understand the Derivation of Each Formula

Rather than memorizing formulas, focus on understanding how they are derived. Knowing the reasoning behind each equation can make it easier to remember and apply in various scenarios. For example, understanding why the area of a triangle is calculated as half of the base times the height can help in recognizing similar problems and adjusting the approach as needed.
Practice Regularly and Apply in Different Contexts
Repetition is key to retaining and mastering any formula. The more frequently you use them in different types of problems, the more comfortable and confident you will become. Consistent practice allows you to recognize when to apply a particular formula and how to adapt it to different situations.
By incorporating these strategies, learners can build a strong foundation for tackling complex mathematical tasks and increase their overall proficiency in solving related problems.
Using Geometry Theorems in Practice
Theorems provide a set of rules that explain how different elements within a shape relate to one another. These principles are essential for solving complex problems, allowing individuals to make logical connections between measurements, angles, and sides. Applying these theorems to real-world scenarios not only enhances problem-solving skills but also helps in understanding how shapes behave in various contexts.
When solving problems, it is crucial to recognize which theorem to apply based on the given information. This often involves identifying known properties and then applying the appropriate rule to find unknown values. Below is an example of how a common theorem is used in practice:
| Theorem | Application | Example Problem | Solution |
|---|---|---|---|
| Pythagorean Theorem | Used to find the length of the sides of a right triangle when two sides are known. | Find the length of the hypotenuse of a right triangle with legs of 3 and 4 units. | The hypotenuse is 5 units, calculated by the formula a² + b² = c² (3² + 4² = 25, √25 = 5). |
By mastering the use of theorems and practicing their application, learners can confidently solve a wide range of problems and build a deeper understanding of the relationships within shapes and spaces.
Solving Equations in Geometry Worksheets
Equations are essential tools in solving various mathematical problems, especially when determining unknown values related to shapes, angles, or dimensions. They represent relationships between different components of a figure and help us apply known values to find the unknowns. Mastering the process of solving equations is a critical skill that allows for precise problem-solving and greater understanding of mathematical concepts.
Step-by-Step Approach to Solving
The process of solving equations involves identifying the right formula, substituting known values, and isolating the unknown variable. Below is an example of how to apply equations in a problem involving the calculation of a triangle’s area:
| Step | Action | Example |
|---|---|---|
| 1 | Identify the formula | Area of a triangle = 1/2 * base * height |
| 2 | Substitute known values | Area = 1/2 * 8 * 5 |
| 3 | Solve for the unknown | Area = 1/2 * 40 = 20 square units |
Common Mistakes to Avoid
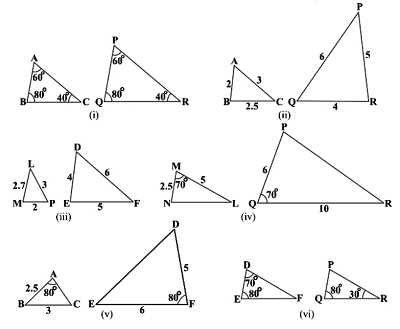
While solving equations, it’s easy to make simple mistakes, such as misapplying formulas or forgetting to square values when necessary. Ensuring that each step is carefully followed and double-checking calculations can help avoid these common errors. Understanding the logic behind the equation is just as important as performing the correct calculations.
By practicing these techniques and following a methodical approach, learners can efficiently solve equations and strengthen their mathematical skills.
Common Challenges in Geometry Problem Solving
Solving mathematical problems that involve shapes, angles, and measurements can present a variety of challenges. Often, the complexity arises not from the difficulty of the individual concepts but from how they are combined or applied in different contexts. Recognizing these challenges early on can help students approach problems more effectively and avoid common pitfalls.
Key Issues Faced in Problem Solving
- Misunderstanding the Problem: Sometimes, the key to solving a problem lies in correctly interpreting the given information. Many mistakes occur when critical details are overlooked or misread.
- Choosing the Right Formula: In some cases, there are multiple formulas available, and selecting the wrong one can lead to incorrect solutions. Understanding the context and what is being asked is essential for choosing the appropriate method.
- Incorrect Calculation: Simple arithmetic errors or missing steps in the calculation process are frequent obstacles. These mistakes can be especially common when handling large numbers or fractions.
- Overlooking Assumptions: Some problems require assumptions to be made, such as assuming a figure is a regular polygon or a triangle has specific properties. Forgetting or misunderstanding these assumptions can result in flawed reasoning.
Overcoming These Challenges
To overcome these challenges, practice and a systematic approach are crucial. Regularly revisiting basic concepts and formulas helps reinforce understanding. Additionally, breaking the problem down into smaller, manageable steps can make complex problems seem less daunting. Here are some strategies to avoid common mistakes:
- Carefully read the problem and highlight important information.
- Check if any assumptions need to be made about the figures involved.
- Double-check all calculations, especially when working with fractions or decimals.
- Review related concepts to ensure the correct formula is being applied.
By staying vigilant and applying these techniques, learners can minimize mistakes and solve problems more efficiently.
How to Improve Your Geometry Skills
Mastering the art of solving problems that involve shapes, angles, and space requires consistent practice and a solid understanding of foundational principles. While the path to proficiency may seem challenging, there are several strategies that can enhance your ability to approach these problems with confidence and accuracy. With the right tools and mindset, anyone can improve their problem-solving abilities in this area.
Building a Strong Foundation
The first step in improving your skills is to ensure that you have a clear understanding of the basic concepts. This includes knowing the different types of shapes, the properties of angles, and the fundamental theorems that apply to various figures. Once you are comfortable with the basics, you can begin to focus on more complex problems. Here are some key steps to build a strong foundation:
- Review key definitions and properties regularly to keep them fresh in your mind.
- Understand the relationships between different shapes and figures.
- Practice visualizing the problem before diving into calculations.
Practical Tips for Improvement
Once you’ve strengthened your foundational knowledge, it’s important to practice solving different types of problems. The more problems you tackle, the more familiar you will become with the various methods of solving them. Here are some additional tips for improving your skills:
- Work through problems step-by-step, and avoid skipping any parts of the process.
- Use diagrams to visualize problems, as this can make complex concepts easier to understand.
- Challenge yourself with increasingly difficult problems to improve both your speed and accuracy.
- Seek help when needed – whether through teachers, online resources, or study groups, discussing problems can provide new insights.
By continuously practicing and applying these strategies, you will steadily enhance your ability to solve problems with ease and confidence.
Geometry Worksheet Solutions for Beginners
For individuals just starting out with solving problems related to shapes, space, and their properties, it’s important to approach each task methodically. With a clear understanding of basic principles, beginners can gradually build confidence and accuracy. Simple problems often involve straightforward calculations, but gaining familiarity with these methods is key to mastering more complex challenges.
Understanding the Basics
The foundation of problem-solving in this area involves knowing the most common shapes and the relationships between their elements, such as sides, angles, and areas. For beginners, focusing on simple calculations such as area and perimeter is a great place to start. To help you get started, here are some simple steps:
- Focus on basic shapes like squares, triangles, and circles.
- Learn and memorize simple formulas for calculating areas and perimeters.
- Understand how to use units of measurement correctly.
Solving Simple Problems
Once the basic concepts are in place, the next step is solving simple problems. By breaking down each problem into smaller, manageable steps, beginners can better understand the approach needed for different types of questions. Remember:
- Start by reading the problem carefully, identifying key information such as dimensions and units.
- Use diagrams to visually represent the problem and highlight important elements.
- Write down the relevant formula or approach that applies to the problem.
With continued practice and persistence, even the most basic challenges can be overcome, setting a solid foundation for tackling more advanced topics in the future.
Advanced Techniques for Geometry Problems
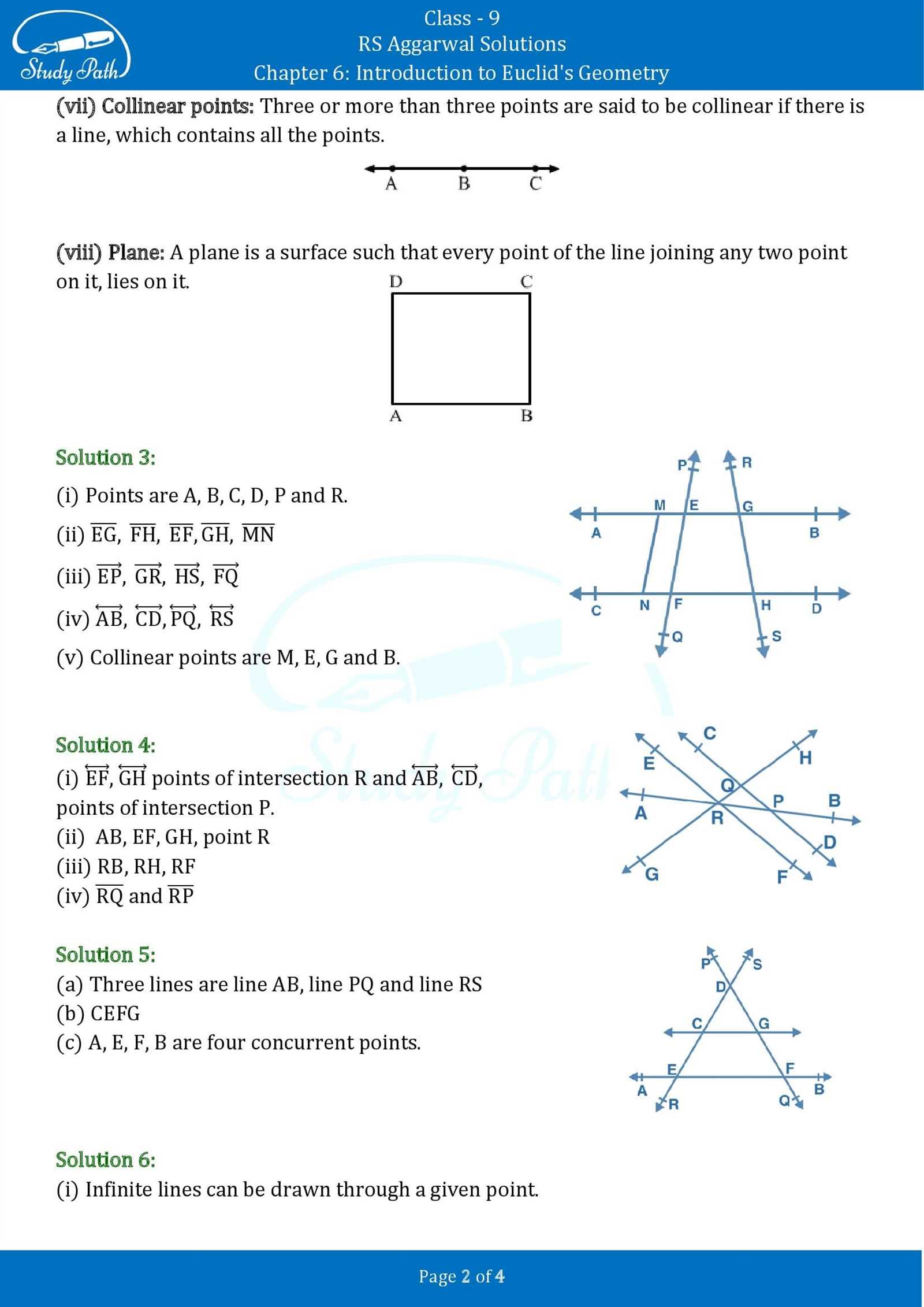
As individuals progress in their problem-solving abilities, tackling more intricate tasks requires a deeper understanding of complex concepts and strategies. Advanced techniques often involve the application of multiple principles in tandem, helping to uncover solutions that may not be immediately obvious. Mastery of these methods allows for greater flexibility and efficiency in solving a wide variety of challenges.
Utilizing Transformations
One powerful approach in solving complex problems is the use of geometric transformations. These operations, such as translations, rotations, reflections, and dilations, enable the reconfiguration of shapes without changing their fundamental properties. By visualizing these transformations, it’s easier to compare different figures and identify relationships between them. The key is to understand how shapes change and how those changes affect distances, angles, and other properties.
- Translation: Shifting a figure without rotating or resizing it.
- Rotation: Turning a shape around a fixed point.
- Reflection: Flipping a figure over a line to create a mirror image.
- Dilation: Scaling a figure up or down while maintaining its shape.
Leveraging Proof Techniques
Another essential skill in solving advanced problems is the ability to construct formal proofs. This process involves logically demonstrating why a particular conclusion is true based on established axioms, definitions, and previously proven theorems. By mastering the art of proof writing, individuals gain the ability to tackle challenging problems systematically and rigorously.
- Direct Proof: Using logical steps to directly prove a statement true.
- Proof by Contradiction: Assuming the opposite of what you want to prove, leading to a contradiction.
- Inductive Proof: Proving that a statement holds for all natural numbers through a base case and inductive step.
Combining these advanced techniques with a solid understanding of fundamental principles provides a strong foundation for solving even the most complex challenges in the subject.
Importance of Practice Sheets
Engaging with practice exercises plays a crucial role in reinforcing understanding and mastering key concepts. Regular practice helps sharpen problem-solving skills, enabling individuals to tackle a variety of challenges with confidence. By revisiting concepts through different scenarios, learners can solidify their grasp on essential topics and build the mental flexibility needed to apply theories effectively.
Repetition through structured activities allows for improved retention of knowledge and better preparation for more complex tasks. It also provides the opportunity to identify areas of weakness and work through them systematically, ensuring that foundational skills are firmly established before progressing to advanced topics.
Benefits of Consistent Practice
One of the most significant advantages of consistent practice is the development of a deeper intuition for the material. As individuals encounter a wide range of problems, they begin to recognize patterns, relationships, and shortcuts that would otherwise remain unnoticed. This makes approaching future challenges more efficient and less intimidating.
- Improved Problem-Solving Speed: Regular exposure to various types of tasks enhances the ability to solve problems quickly and accurately.
- Enhanced Conceptual Understanding: Practice allows learners to move beyond memorization and grasp the underlying principles.
- Increased Confidence: Successfully completing exercises boosts self-assurance and readiness for more challenging scenarios.
Practical Application of Skills

Another important aspect of these activities is their ability to prepare individuals for real-world applications. The ability to apply mathematical concepts in practical settings, such as engineering, architecture, and technology, is invaluable. Through solving varied problems, learners gain the competence necessary to handle practical situations, making practice an essential tool for both academic and professional growth.
How to Check Your Solutions
Verifying your work is an essential part of the problem-solving process. Whether you’re working with calculations, diagrams, or logic, double-checking ensures that your results are correct and reliable. There are several methods you can use to confirm your solutions and identify any potential errors that might have been overlooked.
Steps to Verify Your Results
Following a clear and methodical approach is key when reviewing your work. Below are some common strategies to help check your solutions effectively:
- Revisit the Problem Statement: Ensure that you have interpreted the question correctly and have addressed all aspects of the problem.
- Check Your Calculations: Go through each step of your work and confirm that every calculation follows the correct rules and principles.
- Verify Units and Labels: Make sure all measurements, units, and labels are consistent and appropriately applied throughout your work.
- Look for Logical Consistency: Ensure that your reasoning is sound and follows a clear, logical progression from one step to the next.
Additional Tips for Accuracy
- Use Alternative Methods: If possible, solve the problem using a different method or approach to see if you reach the same result.
- Double-Check Diagrams: If your solution involves geometric figures, ensure that the drawings match the problem’s conditions.
- Ask for Feedback: If you’re unsure about your solution, seek input from others or consult reference materials to verify your findings.
Resources for Further Learning
Expanding your knowledge and skills in mathematical reasoning requires access to various resources. By utilizing different tools and materials, you can deepen your understanding of key concepts and enhance your problem-solving abilities. There are numerous platforms, books, and online materials that offer valuable insights, exercises, and examples to guide your learning journey.
Online Platforms and Courses

- Khan Academy: A free platform offering video tutorials and practice exercises on various topics, ideal for beginners to advanced learners.
- Coursera: A learning platform that provides online courses from universities around the world, including in-depth courses on mathematical theories and techniques.
- edX: Similar to Coursera, this site offers courses and learning materials from top educational institutions, allowing learners to explore advanced mathematical topics.
Books and Reference Materials
- “The Art of Problem Solving” by Richard Rusczyk: A series of books designed to help students tackle complex problems through structured techniques and strategies.
- “Euclid’s Elements” by Euclid: A classic and foundational text in mathematics that explores the fundamental principles of geometry and logical reasoning.
- “Geometry for Dummies” by Mark Ryan: A comprehensive guide that explains geometric concepts in a clear and accessible manner for students at various levels.
Interactive Tools and Apps
- GeoGebra: An interactive app that allows users to explore geometric shapes, graphs, and equations visually, helping to strengthen their understanding.
- Desmos: An online graphing calculator that can be used for plotting geometric figures and solving equations in real time.
How to Approach Tests with Confidence
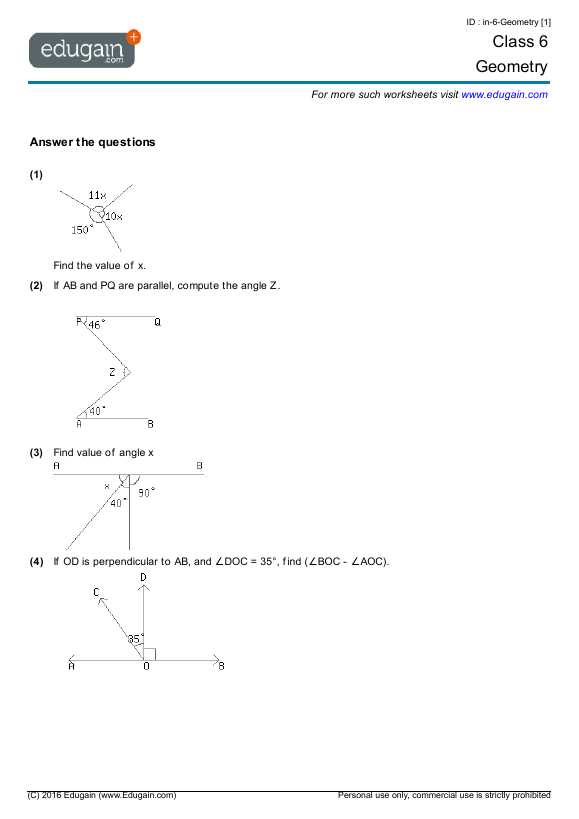
Preparing for and approaching an assessment in mathematical reasoning can feel overwhelming. However, with the right strategies, you can face these challenges confidently. The key is to approach the test with a clear plan, a solid grasp of the material, and a calm mindset. By applying effective study methods, managing your time, and utilizing proven test-taking strategies, you can perform at your best.
Preparation Before the Test
- Review Key Concepts: Make sure to revise essential formulas, theorems, and principles. Understanding the core ideas behind the problems will make solving them easier during the test.
- Practice Regularly: Solve practice problems to identify any weak areas and refine your problem-solving skills. The more problems you work through, the more comfortable you’ll be with various question types.
- Study with a Peer: Discussing problems with classmates can help clarify any doubts and reinforce your understanding. Explaining concepts to others also enhances your retention.
On Test Day
- Read Instructions Carefully: Ensure you understand the question before attempting to answer. Look for specific instructions on what is being asked and any constraints involved.
- Manage Your Time: Allocate a specific amount of time for each section or question. Don’t get stuck on one question for too long; move on and return to it if time permits.
- Double-Check Your Work: If you finish early, review your answers. Look for common mistakes such as calculation errors or missed steps. A fresh set of eyes can help catch oversights.