Understanding fundamental principles in mathematics is essential for building a strong foundation. This section focuses on reinforcing crucial skills and problem-solving techniques that will help you approach complex challenges with confidence. Whether you’re tackling equations, graphing, or simplifying expressions, mastering these skills will prepare you for more advanced topics.
As you work through these exercises, you will become familiar with various methods used to solve different types of problems. With practice, you’ll improve your ability to manipulate and transform mathematical statements into solutions. The goal is not only to solve individual problems but to develop a deeper understanding of the relationships between numbers and operations.
Ready to enhance your skills? By reviewing key ideas and following a systematic approach, you’ll gain the tools necessary for success. Each technique is designed to build upon the previous one, creating a logical progression towards greater proficiency. As you continue practicing, you’ll find that complex tasks become more manageable and intuitive.
Algebra 1 Chapter 4 Review Answers
In this section, we’ll go over key techniques and methods to solve various problems encountered in the fourth section of the course. The goal is to solidify understanding of the concepts and apply them to different scenarios. Mastery of these skills is crucial for moving forward in mathematics and tackling more advanced topics.
Solving Equations and Inequalities
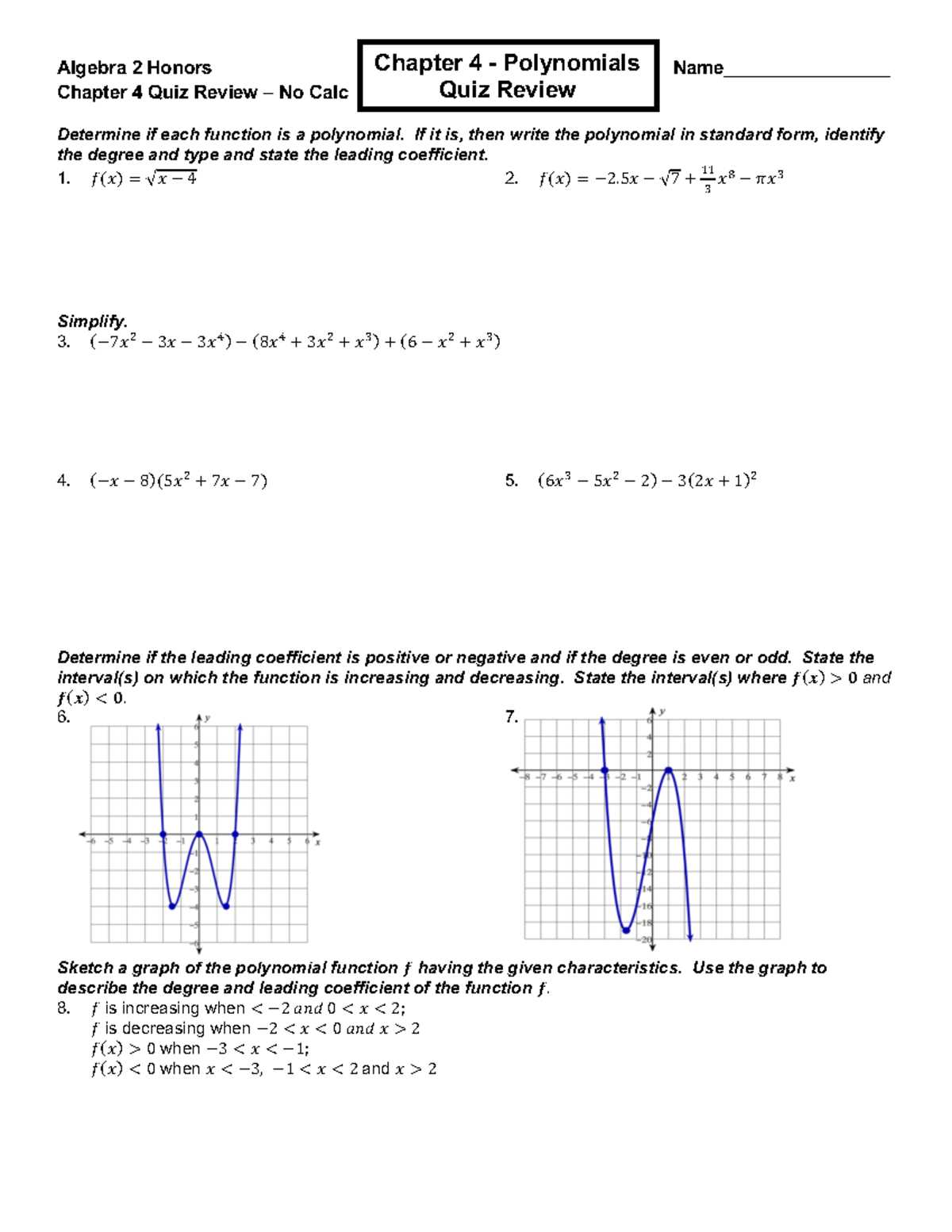
One of the primary skills in this area is solving for unknown values. Whether dealing with simple or complex equations, the process remains the same: isolate the variable and perform operations to find its value. Below are some steps to keep in mind:
- Identify the type of equation or inequality.
- Isolate the variable on one side of the equation.
- Apply operations carefully, ensuring the equation remains balanced.
- Check your solution by substituting it back into the original problem.
Graphing Linear Functions
Graphing functions involves plotting points on a coordinate plane to visually represent relationships between variables. This requires a clear understanding of slopes and intercepts. Here’s a simple approach to graphing:
- Write the equation in slope-intercept form, if possible.
- Identify the slope and the y-intercept.
- Plot the y-intercept on the graph.
- Use the slope to find additional points and draw the line through them.
By practicing these techniques, you’ll not only improve your problem-solving ability but also gain a deeper understanding of mathematical relationships. Consistent practice is key to developing proficiency in these areas.
Key Concepts in Algebra 1 Chapter 4
This section focuses on fundamental ideas that form the backbone of the problems discussed. Gaining a solid understanding of these principles will help in solving various types of mathematical expressions and equations effectively. These concepts are essential for progressing in further mathematical study and applying them to real-world scenarios.
- Solving Linear Equations: The process of isolating variables to find their values. It includes techniques for working with one-variable and multi-variable expressions.
- Graphing Functions: Understanding how to plot and interpret lines on a coordinate plane by identifying slope and y-intercept.
- Inequalities: Techniques for solving and graphing inequalities, understanding their implications on number ranges.
- Factoring Expressions: Breaking down complex algebraic expressions into simpler components for easier manipulation and solution finding.
- Working with Rational Expressions: Simplifying, multiplying, dividing, and adding fractions that contain variables.
Mastering these concepts will not only aid in solving problems but also enhance your ability to approach more intricate mathematical challenges. These ideas act as building blocks for tackling more advanced topics and refining problem-solving strategies.
Solving Linear Equations Explained
Linear equations involve relationships where the highest exponent of the variable is one. The goal is to find the value of the unknown that satisfies the equation. These types of problems often follow a straightforward process, where each step involves isolating the variable and performing operations to maintain equality on both sides of the equation.
To solve such equations, you must follow a logical sequence of steps:
- Identify the variable: The first step is recognizing the unknown value in the equation.
- Eliminate constants: Move any constants to one side of the equation by adding or subtracting them from both sides.
- Isolate the variable: Use multiplication or division to isolate the variable, ensuring it stands alone on one side of the equation.
- Check your solution: After determining the variable’s value, substitute it back into the original equation to verify the correctness of your solution.
Example: For the equation 2x + 5 = 15, you would subtract 5 from both sides to get 2x = 10, then divide both sides by 2, resulting in x = 5. This solution can be verified by substituting 5 back into the original equation.
By practicing these steps, you’ll become more proficient at solving linear equations and better equipped to handle more complex expressions in the future.
Understanding Functions and Their Graphs
Functions represent a relationship where each input corresponds to exactly one output. These mathematical models are crucial for expressing how one quantity depends on another. The ability to graph these relationships visually helps to understand their behavior and make predictions based on the data.
Graphing a function involves plotting points on a coordinate plane. The horizontal axis represents the input values, while the vertical axis represents the outputs. By connecting these points, you can see the pattern or trend that the function describes. Each type of function will produce a different shape on the graph, such as a straight line, curve, or step pattern.
Understanding the structure of a function allows you to predict the outcome for any given input, making it easier to solve problems and analyze relationships. As you explore more functions, you will encounter different types of graphs, such as linear, quadratic, and exponential, each with its own set of properties and rules for interpretation.
Operations with Algebraic Expressions
When working with mathematical expressions that include variables and constants, a variety of operations can be applied to simplify or manipulate the terms. These include addition, subtraction, multiplication, and division. The goal is to transform complex expressions into simpler forms that are easier to evaluate or solve, which is essential for understanding mathematical relationships and solving equations.
Basic Mathematical Operations
The following operations are commonly used in manipulating expressions with variables:
| Operation | Description | Example |
|---|---|---|
| Addition | Combining terms that have the same variable or constant. | 4x + 3x = 7x |
| Subtraction | Removing or reducing terms with similar variables. | 5y – 2y = 3y |
| Multiplication | Multiplying constants or variables together. | 2a * 3b = 6ab |
| Division | Dividing terms with the same variable or constant. | 12x ÷ 3x = 4 |
Simplifying Expressions by Combining Like Terms
One of the most important steps in simplifying expressions is combining like terms. Like terms are terms that contain the same variable raised to the same power. For example, in the expression 2x + 5x – 3x, all terms contain the variable x, so they can be combined to give 4x.
By understanding and applying these basic operations, you can simplify expressions and equations more efficiently. This skill is a fundamental part of solving more complex problems in mathematics and beyond.
Working with Rational Expressions
Rational expressions are fractions that involve polynomials in both the numerator and the denominator. Simplifying, multiplying, dividing, and adding or subtracting these types of expressions requires understanding the properties of polynomials and how they interact. The goal is to work with these expressions in a way that makes solving equations or simplifying mathematical relationships easier and more efficient.
When working with these types of expressions, the first step is often to factor both the numerator and denominator when possible. By factoring, you can identify common factors that can be canceled out, which simplifies the expression. For instance, a rational expression like (x² – 9) / (x + 3) can be simplified by factoring the numerator as (x – 3)(x + 3), resulting in x – 3 after canceling the common factor (x + 3).
Understanding how to work with rational expressions is critical for solving problems that involve ratios, rates, or proportions. Mastering operations such as addition, subtraction, multiplication, and division is key to progressing in more complex areas of mathematics and real-world applications.
Solving Word Problems Step-by-Step
Word problems often present real-life scenarios that require translating verbal information into mathematical expressions. The key to solving these problems is breaking them down into manageable steps. By following a systematic approach, you can better understand the problem and identify the right mathematical operations to use. This process helps you convert complex situations into solvable equations or expressions.
The first step in solving a word problem is to carefully read the problem and highlight important information such as numbers, units, and relationships. Next, define the unknowns and decide what you’re trying to find. Afterward, translate the problem into an equation or expression using the information gathered. Once you have an equation, solve it using appropriate methods, such as addition, subtraction, multiplication, or division, depending on what the problem asks. Finally, check your solution by revisiting the problem and ensuring that your answer makes sense in the given context.
Example Word Problem: A car travels at a speed of 60 miles per hour. How long will it take for the car to travel 240 miles?
Steps to Solve:
- Step 1: Identify the given information: Speed = 60 miles/hour, Distance = 240 miles.
- Step 2: Define the unknown: Time = ?
- Step 3: Set up the equation: Time = Distance ÷ Speed.
- Step 4: Substitute the known values: Time = 240 ÷ 60.
- Step 5: Solve the equation: Time = 4 hours.
By following these steps, you can confidently approach and solve a variety of word problems in different contexts.
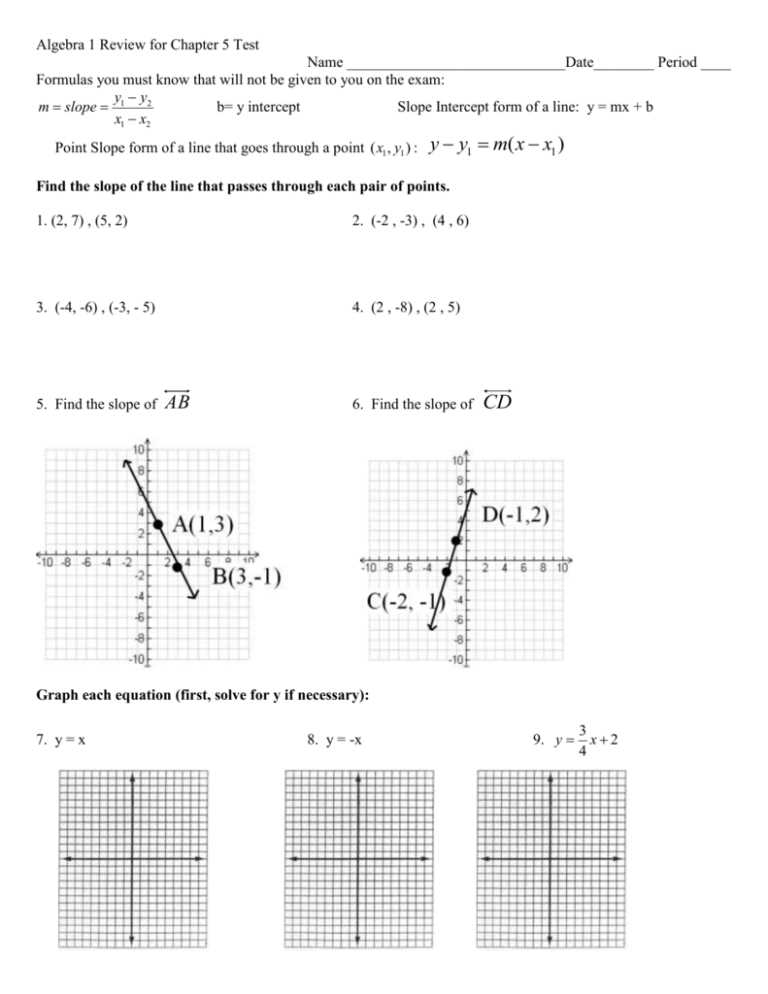
Identifying Slope and Intercepts
Understanding how to determine the slope and intercepts of a linear equation is essential for analyzing the behavior of straight lines on a graph. The slope represents the rate of change, showing how much one variable increases or decreases in relation to another. The intercepts, on the other hand, indicate where the line crosses the axes. By examining these key features, you can gain valuable insights into the relationship between variables and graph linear equations accurately.
Finding the Slope
The slope of a line measures how steep the line is and is often represented by the letter m. To find the slope, you need two points on the line. The formula for slope is:
m = (y₂ – y₁) / (x₂ – x₁)
Where (x₁, y₁) and (x₂, y₂) are the coordinates of two points on the line. The slope tells you how much the y-coordinate changes for every unit increase in the x-coordinate.
Finding the Intercepts
The intercepts are the points where the line crosses the axes. There are two types of intercepts to identify:
- Y-Intercept: This is the point where the line crosses the y-axis. To find the y-intercept, set x = 0 and solve for y.
- X-Intercept: This is the point where the line crosses the x-axis. To find the x-intercept, set y = 0 and solve for x.
| Point on Line | Calculation | Intercept |
|---|---|---|
| (0, 3) | x = 0, solve for y | Y-Intercept = 3 |
| (4, 0) | y = 0, solve for x | X-Intercept = 4 |
By identifying the slope and intercepts, you can graph linear equations with ease and better understand the relationship between the variables in the equation.
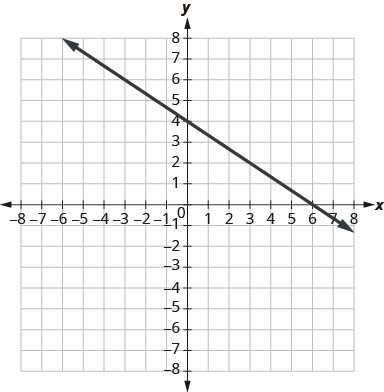
Graphing Linear Equations on a Plane
Graphing a linear equation on a plane involves plotting points based on the equation and drawing a straight line through them. This visual representation helps to understand the relationship between two variables. By following specific steps, you can transform an equation into a graph that shows the connection between the x and y values. This is essential for analyzing trends and making predictions based on the data.
To graph an equation, start by identifying key components, such as the slope and intercepts, which provide the foundation for drawing the line. Once you have these values, it becomes easier to determine the line’s position and direction on the coordinate plane.
Steps to Graph a Linear Equation
- Start by rewriting the equation in slope-intercept form: y = mx + b, where m is the slope and b is the y-intercept.
- Plot the y-intercept b on the graph. This is where the line crosses the y-axis.
- Use the slope m to determine the direction of the line. The slope is a ratio of the rise (change in y) to the run (change in x).
- Plot another point using the slope and draw a straight line through the points.
- Extend the line in both directions to complete the graph.
Example
Consider the equation y = 2x + 1.
| Step | Action | Result |
|---|---|---|
| 1 | Identify slope and y-intercept | Slope = 2, Y-Intercept = 1 |
| 2 | Plot y-intercept (0, 1) | Point (0, 1) on the graph |
| 3 | Use slope to plot second point | Rise = 2, Run = 1. Second point: (1, 3) |
| 4 | Draw a line through the points | Straight line passing through (0, 1) and (1, 3) |
By following these steps, you can accurately graph any linear equation on a plane and visually interpret the relationship between the variables. This process is crucial for understanding trends and solving real-world problems based on mathematical equations.
Systems of Equations Simplified
When working with multiple relationships involving variables, you often encounter a set of equations that must be solved simultaneously. These systems of equations can be solved using different methods to find the values of the variables that satisfy all equations in the set. Understanding the process can simplify solving real-world problems that involve multiple constraints or conditions.
The goal is to find a common solution, where the values for each variable make all the equations in the system true. There are several techniques for solving these systems, including substitution, elimination, and graphing. Each method provides a systematic approach to determine the values that satisfy the entire set of equations.
Methods to Solve Systems of Equations
- Substitution: This method involves solving one equation for one variable and substituting that expression into the other equation.
- Elimination: In this approach, you manipulate the equations to eliminate one of the variables by adding or subtracting the equations.
- Graphing: By graphing both equations on the same coordinate plane, the point where the lines intersect represents the solution.
Example of Solving a System
Consider the following system of equations:
| Equation | Step | Explanation |
|---|---|---|
| 2x + y = 8 | Step 1 | Choose one equation to solve for one variable. For example, solve the first equation for y: y = 8 – 2x. |
| 3x – y = 4 | Step 2 | Substitute y = 8 – 2x into the second equation: 3x – (8 – 2x) = 4. |
| Step 3 | Simplify the equation: 3x – 8 + 2x = 4 → 5x = 12 → x = 12/5. | |
| Step 4 | Substitute x = 12/5 back into y = 8 – 2x: y = 8 – 2(12/5) = 8 – 24/5 = 40/5 – 24/5 = 16/5. |
The solution to the system is x = 12/5 and y = 16/5. These values satisfy both equations in the system, providing the solution to the problem.
By using these techniques, solving a system of equations becomes a more straightforward process, whether you are dealing with two variables or more complex systems.
Solving Inequalities in Algebra 1

In many situations, we are not looking for an exact solution, but rather a range of possible values that satisfy certain conditions. Inequalities help represent these types of problems, where one value is not necessarily equal to another, but is instead greater than, less than, or related in another way. Solving these expressions involves determining the set of values that fulfill the given condition, which is crucial for understanding many real-world applications.
To solve inequalities, you typically perform similar steps as you would for equations, but there are important differences, particularly when it comes to multiplying or dividing by negative numbers, which reverses the inequality sign.
Steps for Solving Inequalities
- Isolate the variable: Just like solving an equation, start by isolating the variable on one side of the inequality.
- Perform operations: Use addition, subtraction, multiplication, or division to simplify the inequality. However, remember to reverse the inequality sign when multiplying or dividing by a negative number.
- Check the solution: After finding the variable’s possible values, test them to ensure they satisfy the original inequality.
Example of Solving an Inequality
Consider the inequality: 3x – 5 > 7
- Step 1: Add 5 to both sides: 3x > 12
- Step 2: Divide both sides by 3: x > 4
- Step 3: The solution is x > 4, meaning any value greater than 4 satisfies the inequality.
In this case, the solution is expressed as a range of values rather than a single number, indicating all the possible values for the variable.
Understanding and solving inequalities is a fundamental skill for handling a wide variety of problems, from determining profit margins to calculating distances or time intervals. Mastering this concept provides a strong foundation for more complex topics in mathematics.
Factoring Techniques for Beginners
Factoring is a crucial skill in simplifying expressions and solving equations. It involves breaking down complex terms into simpler factors that, when multiplied together, give the original expression. Understanding basic factoring techniques is essential for progressing in mathematics, as it helps in solving quadratic equations, simplifying expressions, and finding solutions to various problems.
Common Factoring Methods
There are several methods for factoring, each suited for different types of expressions. Below are the most commonly used techniques:
- Finding the Greatest Common Factor (GCF): The first step in factoring any expression is to identify the greatest common factor of all terms. By factoring out the GCF, you can simplify the expression and make further factoring easier.
- Factoring Trinomials: This method is used when the expression is a trinomial (three terms). For example, factoring expressions like x² + 5x + 6 requires finding two numbers that multiply to give the constant term and add to give the middle term.
- Difference of Squares: This technique is used when you have two perfect squares separated by a subtraction sign, such as x² – 9. The result is a binomial factorization like (x – 3)(x + 3).
Example of Factoring a Trinomial
Consider the trinomial: x² + 7x + 12
- Identify two numbers that multiply to 12 (the constant term) and add to 7 (the middle term). These numbers are 3 and 4.
- Rewrite the expression as (x + 3)(x + 4).
Thus, x² + 7x + 12 = (x + 3)(x + 4).
By practicing these factoring techniques, you can quickly simplify expressions and solve various types of equations. Mastering these methods is an important step in developing a strong mathematical foundation.
Exponents and Their Rules
Exponents are a powerful tool in mathematics, used to represent repeated multiplication of a number by itself. Understanding the rules that govern exponents is essential for simplifying expressions and solving problems involving powers. These rules provide a structured way to handle operations involving exponential terms, making complex calculations easier and more manageable.
Basic Exponent Rules
There are several key rules to follow when working with exponents:
- Product of Powers Rule: When multiplying two terms with the same base, add the exponents. For example, x⁴ * x² = x⁶.
- Quotient of Powers Rule: When dividing two terms with the same base, subtract the exponents. For example, x⁶ ÷ x² = x⁴.
- Power of a Power Rule: When raising an exponent to another exponent, multiply the exponents. For example, (x²)³ = x⁶.
- Power of a Product Rule: When raising a product to a power, apply the exponent to each factor inside the parentheses. For example, (xy)² = x²y².
- Zero Exponent Rule: Any non-zero number raised to the power of zero is equal to one. For example, x⁰ = 1.
Example Problems
Let’s apply the exponent rules to some sample problems:
- Problem 1: Simplify x³ * x². Using the product of powers rule: x³ * x² = x⁵.
- Problem 2: Simplify y⁵ ÷ y². Using the quotient of powers rule: y⁵ ÷ y² = y³.
- Problem 3: Simplify (z²)⁴. Using the power of a power rule: (z²)⁴ = z⁸.
By following these rules, you can simplify expressions involving exponents quickly and accurately, making complex calculations more straightforward.
Understanding Absolute Value Functions

Absolute value functions represent a relationship where the output is always non-negative, regardless of whether the input is positive or negative. These functions are particularly useful for modeling situations where only the magnitude of a quantity matters, such as distances or deviations from a certain point. The graph of an absolute value function has a distinctive V-shape, reflecting the way the function handles both positive and negative values symmetrically.
To explore absolute value functions, consider the general form of the equation: f(x) = |x – h| + k. In this form, h represents the horizontal shift, and k is the vertical shift. These shifts determine the location of the vertex, which is the point where the graph changes direction. The function f(x) = |x| is the simplest form, where the graph has a vertex at the origin and opens upwards.
The key characteristic of absolute value functions is that they transform negative values into positive ones. For example, in the function f(x) = |x – 3|, any value of x greater than or equal to 3 results in a non-negative output. For values of x less than 3, the output is still positive, as the absolute value operation reflects the number’s distance from 3 on the number line.
Graphically, the absolute value function creates a sharp turn at its vertex, showing that the value of f(x) never becomes negative. This makes it a valuable tool for situations where negative values are not meaningful, such as measuring physical quantities like length or time.
Polynomial Operations and Simplifications
Working with polynomials involves performing various operations such as addition, subtraction, multiplication, and division. These operations allow for the manipulation and simplification of polynomial expressions, making them easier to work with in mathematical problems. Understanding how to handle polynomials efficiently is crucial for solving more complex equations and inequalities.
Adding and Subtracting Polynomials
When adding or subtracting polynomials, the key is to combine like terms. Like terms are terms that have the same variable raised to the same power. For instance, when adding 3x^2 + 2x and 4x^2 – 5x, the like terms 3x^2 and 4x^2 are combined, and the like terms 2x and -5x are also combined. This results in:
| Expression | Result |
|---|---|
| 3x² + 2x + 4x² – 5x | 7x² – 3x |
Multiplying Polynomials
When multiplying polynomials, the distributive property is applied. Each term in one polynomial is multiplied by every term in the other polynomial. For example, multiplying (x + 2)(x – 3) involves distributing each term in the first set of parentheses to every term in the second set:
| Expression | Steps | Result |
|---|---|---|
| (x + 2)(x – 3) | x(x – 3) + 2(x – 3) | x² – 3x + 2x – 6 |
After combining the like terms, the simplified result is x² – x – 6.
Mastering these basic polynomial operations is essential for simplifying expressions and solving higher-level problems in mathematics.
Quadratic Equations and Solutions
Quadratic equations are expressions where the highest power of the variable is squared. These types of equations often arise in various mathematical contexts, such as projectile motion, area problems, and optimization scenarios. Solving these equations involves finding the values of the variable that satisfy the equation, often referred to as the “roots” or “solutions.” There are multiple methods available to solve quadratic equations, depending on the structure and complexity of the equation.
The most common methods for solving quadratic equations include factoring, using the quadratic formula, and completing the square. Each method has its advantages, depending on the equation’s form. Understanding when and how to apply each technique is crucial for finding the correct solutions.
Factoring Method
Factoring is one of the simplest ways to solve quadratic equations when the equation can be expressed as a product of two binomials. For example, consider the equation:
x² + 5x + 6 = 0
To solve this equation, we look for two numbers that multiply to 6 and add to 5. These numbers are 2 and 3, so the factored form of the equation is:
(x + 2)(x + 3) = 0
By setting each factor equal to zero, we find the solutions:
x + 2 = 0 or x + 3 = 0
Thus, the solutions are x = -2 and x = -3.
Using the Quadratic Formula
When factoring is not possible or practical, the quadratic formula provides a reliable solution method. The quadratic formula is:
x = (-b ± √(b² – 4ac)) / 2a
For the equation ax² + bx + c = 0, the values of a, b, and c are substituted into the formula. As an example, for the equation:
x² – 4x – 5 = 0
We identify a = 1, b = -4, and c = -5. Plugging these into the quadratic formula, we get:
x = (4 ± √((-4)² – 4(1)(-5))) / 2(1)
Solving this, we find:
x = (4 ± √(16 + 20)) / 2
x = (4 ± √36) / 2
x = (4 ± 6) / 2
This gives two possible solutions: x = (4 + 6) / 2 = 5 and x = (4 – 6) / 2 = -1. Therefore, the solutions are x = 5 and x = -1.
These methods, along with a thorough understanding of the concepts behind quadratic equations, are essential tools for solving problems involving quadratic relationships.
Tips for Algebra 1 Chapter 4 Success
Mastering the concepts covered in this section can be challenging, but with the right strategies and approach, success is achievable. To improve your understanding and performance, it’s important to adopt effective study habits, develop problem-solving skills, and practice regularly. Below are some tips that can help you navigate through the material and achieve your best results.
Study Strategies
- Review Key Concepts Regularly: Ensure you have a clear grasp of foundational principles, as these concepts are built upon in more complex problems. Understanding the basics thoroughly will make the more advanced topics easier to grasp.
- Break Down Complex Problems: When faced with a difficult problem, break it into smaller, manageable steps. Solve each part before moving on to the next. This approach reduces confusion and keeps you focused.
- Practice with Examples: Practice makes perfect. Work through various example problems, especially those that challenge you. The more you practice, the more confident you’ll become in applying the techniques.
- Use Visual Aids: Graphs and diagrams can help visualize abstract concepts, such as equations or functions. Creating visual representations can often provide insight that is not immediately obvious from the equations alone.
Effective Problem-Solving Techniques
- Understand the Problem Before Solving: Always read the question carefully and identify what is being asked. Understanding the problem helps you choose the right approach to solve it.
- Work Systematically: Approach each problem step-by-step. Write down each step of your work and check for mistakes as you go. This minimizes errors and ensures accuracy.
- Check Your Work: Once you have completed a problem, take the time to review your steps. This helps catch mistakes and ensures your solution is correct.
- Seek Help When Stuck: If you encounter a particularly difficult problem, don’t hesitate to ask for help. Whether it’s from a teacher, tutor, or study group, getting clarification on tough concepts can make a big difference.
Time Management
- Allocate Specific Study Times: Set aside time each day to focus on the material. Consistency is key in mastering new concepts.
- Don’t Cram: Avoid waiting until the last minute to study. Cramming often leads to stress and poor retention. Instead, spread your study sessions out over several days or weeks.
- Practice Under Timed Conditions: When preparing for assessments, simulate test conditions by practicing problems under timed conditions. This helps improve both your speed and accuracy.
By implementing these tips, you can improve your understanding of the material and enhance your ability to tackle problems effectively. Stay consistent, be patient with yourself, and keep practicing to achieve success in this section.