Edgenuity Algebra 1 Final Exam Answers Guide

Successfully completing assessments in mathematics requires more than just memorization. It’s about understanding key principles and knowing how to apply them under time constraints. To excel, it’s important to approach these evaluations with a clear strategy that allows for both speed and accuracy. In this guide, we’ll explore useful techniques that will enhance your preparation for this important evaluation.

Mastering core concepts is crucial, as each question is designed to test your ability to think critically and solve problems effectively. While some may be straightforward, others may require a deeper understanding or the application of multiple concepts. Knowing where to focus your attention can make all the difference in performing well.

Practice is a key factor in mastering any subject, and consistent review of previous materials can help you feel more confident. With the right approach, you’ll not only improve your problem-solving skills but also reduce stress when it comes time to demonstrate what you’ve learned.

Edgenuity Algebra 1 Final Exam Answers

Success in your mathematics assessment depends on a combination of preparation, understanding core concepts, and the ability to apply knowledge in problem-solving scenarios. To excel, it’s essential to recognize the types of questions that are likely to appear and develop strategies for tackling them. This section will provide valuable insight into how to approach the most common question formats and the key topics that are often tested.

Key Topics to Focus On

Some areas are more likely to be tested than others. A strong understanding of equations, functions, and basic operations is critical. Pay special attention to linear equations, inequalities, and graphing. These concepts form the foundation of many problems and are often revisited in various forms. Moreover, make sure to review systems of equations, polynomial expressions, and the rules of exponents as these topics frequently appear in different question types.

Effective Study Strategies

Strategic preparation can make a big difference. Start by practicing with sample problems and reviewing any homework assignments or quizzes. Focus on areas where you struggle the most and make sure to understand each solution thoroughly. Use available resources such as online tutorials, practice tests, or study groups to reinforce your skills. Additionally, time yourself while working through problems to build both speed and confidence for the actual assessment.

Understanding Edgenuity Algebra 1 Format

Familiarity with the structure of a mathematics assessment is crucial for achieving success. Understanding the format allows students to approach each section confidently and efficiently. Each test is designed to evaluate different skills and concepts, and knowing what to expect can make a significant difference in performance. In this section, we’ll explore the key components of the test and how to navigate them.

Question Types: Expect a mix of multiple-choice questions, fill-in-the-blank, and problem-solving tasks. The format tests both theoretical knowledge and practical application.
Level of Difficulty: Questions will vary in difficulty, starting with foundational concepts and progressing to more complex problems. Being able to identify which questions to tackle first is a helpful strategy.
Time Management: Efficiently allocating your time across different sections is essential. Each question should be answered within a set amount of time to avoid running out of time during the assessment.
Navigation: The format allows you to easily navigate between questions, so if you are unsure about a specific problem, you can skip it and return later.

Knowing the format of the test ahead of time will help reduce anxiety and allow for a more focused approach. Practice with similar question types and review areas where you may have weaknesses to ensure you’re fully prepared when it’s time to take the assessment.

How to Approach Final Exam Questions

Effectively approaching each question during an assessment requires strategy, focus, and a clear understanding of the problem. A thoughtful method can help you navigate through challenges and maximize your performance. In this section, we will cover practical techniques that will help you tackle various question types efficiently and confidently.

Preparation Before the Test

Review Key Concepts: Focus on the most important topics that are likely to appear. Understand the underlying principles, not just the formulas.
Practice Problem-Solving: Solve problems similar to those you expect on the test. The more practice you get, the faster you’ll be at recognizing patterns and solving problems.
Simulate Test Conditions: Time yourself while practicing to replicate the pressure of the real assessment.

During the Test

Read Carefully: Read each question thoroughly before attempting to solve it. This will help you avoid making careless mistakes.
Start with Easier Questions: Begin with problems you feel confident about to build momentum and reduce anxiety.
Use Process of Elimination: For multiple-choice questions, eliminate obviously wrong options first, narrowing down your choices.
Manage Your Time: Don’t spend too long on any one question. If you’re stuck, move on and come back to it later.
Double-Check Your Work: If time permits, go back and review your answers, especially for complex problems.

By following these strategies, you’ll be better equipped to handle any question that comes your way, ensuring a more successful outcome.

Key Concepts for Algebra 1 Success

Mastering fundamental mathematical concepts is essential for performing well in assessments. These core ideas serve as the building blocks for more advanced topics and are crucial to solving problems accurately. In this section, we will highlight the key principles that are fundamental to achieving success and excelling in your mathematical studies.

Linear Equations: Understanding how to solve equations with one variable is critical. Be familiar with both one-step and multi-step equations and how to isolate the variable.
Inequalities: Learning to solve and graph inequalities is essential. Focus on the different methods for solving, including compound inequalities and systems of inequalities.
Functions: Understanding the concept of a function, how to graph them, and how to use function notation will help you tackle more complex problems.
Exponents and Powers: Master the rules for manipulating exponents and powers, including multiplication, division, and raising powers to powers.
Polynomials: Know how to add, subtract, and multiply polynomials. Be able to factor simple polynomials and apply them in solving equations.
Factoring: Being able to factor expressions, such as quadratics, and solve equations by factoring is a crucial skill.
Graphing: Understand how to plot points on a coordinate plane and interpret the graphs of equations, including identifying slopes and intercepts.

Mastering these concepts not only prepares you for the assessment but also provides a strong foundation for tackling more complex mathematical challenges in the future.

Common Mistakes on the Final Exam

While preparing for an important mathematical assessment, it’s crucial to be aware of common errors that many students make. These mistakes can often be avoided with careful attention to detail and a solid understanding of the material. In this section, we will discuss some of the most frequent pitfalls that students encounter during testing and how to avoid them.

Misreading Questions: One of the most common mistakes is not carefully reading the entire question. Skipping over important details or failing to understand the exact requirements can lead to incorrect answers.
Calculation Errors: Simple arithmetic mistakes, such as adding or multiplying incorrectly, can result in a wrong answer. Always double-check calculations to ensure accuracy.
Incorrectly Applying Formulas: Many students struggle with properly applying formulas to problems. It’s important to remember the correct steps and substitute values carefully.
Forgetting to Simplify: After solving an equation, some students forget to simplify their answers, which may lead to unnecessary mistakes. Always simplify your final expression where possible.
Overlooking Signs: Neglecting negative signs, particularly when dealing with subtraction or negative numbers, is a common error that can drastically change the outcome of a problem.
Misinterpreting Graphs: Interpreting graphs and charts incorrectly can lead to incorrect conclusions. Ensure you understand how to read graphs and identify key points accurately.
Panic Under Time Pressure: Stress and time constraints can cause mistakes, especially when rushing through questions. It’s important to stay calm, read each question carefully, and pace yourself throughout the test.

By staying mindful of these common mistakes and practicing good test-taking habits, you can significantly improve your chances of achieving a successful result.

Practice Questions and Their Importance

Practicing problems before a major assessment is one of the most effective ways to reinforce your understanding of key concepts. It helps to solidify what you have learned, identify areas where you need improvement, and increase your confidence. In this section, we will explore the value of practice questions and how they contribute to better performance on the actual test.

Reinforcing Key Skills

Solving practice problems helps to reinforce the core skills needed for problem-solving. By working through a variety of question types, you can become more familiar with the format of the problems, the steps required to solve them, and the common techniques used in their solutions. Repetition of these tasks ensures that the knowledge becomes second nature.

Identifying Weak Areas

While practicing, you may encounter areas that still feel challenging or unclear. These are the sections that need more attention. Identifying weak points early allows you to focus your study time more efficiently and target the specific concepts or methods that require improvement.

In addition to improving accuracy, practicing questions under timed conditions can help you manage your pace and perform under pressure, giving you an advantage when it comes time to take the real assessment.

Time Management During the Exam

Effective time management is a critical component of performing well in any assessment. Being able to pace yourself allows you to approach each question thoughtfully while ensuring you have enough time to complete everything. In this section, we will discuss how to organize your time, prioritize questions, and avoid rushing through problems.

Proper time allocation starts before the test begins. When you receive the test, take a moment to survey the questions and assess their difficulty. Divide the available time based on how many questions are on the test and the complexity of the problems. A clear plan will help you stay on track and ensure that no question is left unfinished.

Section	Time Allocation	Strategy
Easy Questions	25% of time	Answer these first to build momentum and boost confidence.
Moderate Difficulty Questions	50% of time	Allocate the majority of your time to these, as they make up the core of the test.
Challenging Questions	25% of time	Spend the remaining time on more difficult problems, returning to them after completing easier questions.

By dividing your time according to the difficulty of the questions, you will prevent spending too much time on any one problem. This strategy helps reduce anxiety and increases your chances of completing the test with a strong performance.

Using Online Resources for Help

The internet offers a wealth of educational tools and platforms that can be invaluable when preparing for a test. Whether you’re seeking clarification on a specific topic or practicing with additional problems, online resources provide flexible and accessible support. In this section, we’ll explore how you can use these tools to enhance your understanding and boost your performance.

Interactive Tutorials: Websites offering step-by-step tutorials can help break down complex concepts into manageable pieces. These resources often include video lessons, diagrams, and examples that allow you to learn at your own pace.

Online Practice Tests: Many platforms provide free practice tests or quizzes that mimic the structure and difficulty of real assessments. Taking these tests under timed conditions will not only help you practice but also improve your test-taking skills and boost confidence.

Discussion Forums and Study Groups: Joining online study communities or forums can connect you with others who are facing similar challenges. Engaging in discussions and sharing problem-solving strategies with peers can help deepen your understanding of tricky topics.

Educational Apps: Mobile apps designed for learning offer a convenient way to review concepts on the go. Many apps have built-in quizzes, flashcards, and games that make studying both fun and effective.

By using these online resources effectively, you can complement your study routine, clarify doubts, and improve your overall preparation, all while benefiting from a range of learning styles and tools.

How to Prepare for the Exam Effectively

Proper preparation is key to succeeding in any important assessment. The process involves not only understanding the material but also organizing your study time and employing effective techniques to reinforce your knowledge. In this section, we will explore practical strategies that will help you study more efficiently and confidently approach the test.

Create a Study Plan

One of the first steps in preparing effectively is to create a clear and structured study plan. Break down the topics into smaller sections and allocate specific time slots for each. This will help you stay focused and prevent last-minute cramming. Be sure to allow time for breaks to avoid burnout and to ensure your mind stays fresh.

Focus on Understanding Concepts

Instead of simply memorizing formulas or procedures, focus on understanding the underlying concepts. Grasping the “why” behind each method allows you to apply it more flexibly during the assessment. Use examples and practice problems to solidify your comprehension of each topic.

Incorporating these strategies into your routine will help ensure that you are fully prepared, confident, and ready to tackle any challenge the assessment may present.

Algebra 1 Topics You Must Know

Mastering certain key topics is essential for success in any mathematical assessment. These foundational concepts not only appear frequently on assessments but are also integral to understanding more advanced topics in mathematics. Below is a list of must-know topics that will help you perform confidently in any related evaluation.

Linear Equations: Understanding how to solve equations involving variables and constants, and graphing them on the coordinate plane.
Exponents and Powers: Knowing the laws of exponents, including how to simplify expressions with powers and roots.
Polynomials: Recognizing and simplifying polynomial expressions, including addition, subtraction, and multiplication.
Factoring: Breaking down complex expressions into simpler factors, particularly quadratics and other binomials.
Inequalities: Solving and graphing inequalities on number lines, including systems of inequalities.
Rational Expressions: Understanding how to simplify and operate with fractions that have polynomials in the numerator or denominator.
Systems of Equations: Solving systems of linear equations using methods like substitution and elimination.
Functions and Graphs: Recognizing and interpreting functions, as well as graphing linear and non-linear equations.

By focusing on these fundamental areas, you will not only improve your problem-solving abilities but also build a strong foundation for more complex mathematical concepts in the future. Practice with a variety of problems to ensure you fully understand each topic and its applications.

How to Check Your Work on the Test

Checking your work is a crucial step to ensure accuracy and improve your score on any assessment. After completing each question, it’s important to go over your solutions carefully to identify and correct any mistakes. In this section, we will discuss effective strategies for reviewing your answers and minimizing errors before submitting your test.

1. Review Your Calculations: Start by revisiting the calculations for each problem. Pay close attention to each step to ensure you didn’t make simple arithmetic errors. Even small mistakes can lead to incorrect answers, so double-checking can save you valuable points.

2. Verify Units and Notation: Make sure all units are correct and consistent throughout the test. For example, if you are working with measurements or word problems, check that the units match the requirements of the problem. Additionally, ensure that you’ve used proper mathematical notation, including correct symbols and formatting.

3. Check for Reasonableness: Assess whether your answers make sense in the context of the problem. For instance, if a problem asks for a positive number, but you end up with a negative result, it could indicate an error in your solution. Reviewing the reasonableness of your answer can help catch obvious mistakes.

4. Work Backwards (Where Applicable): For some problems, you can use the reverse process to check your work. For example, if you solved an equation, substitute your answer back into the original equation to see if it holds true. This technique can help confirm that your solution is correct.

By implementing these strategies, you can catch any overlooked mistakes and ensure your answers are as accurate as possible before submitting your test.

Strategies for Answering Multiple-Choice Questions

Multiple-choice questions can be challenging, but with the right approach, they become much easier to navigate. The key is to have a strategy that helps you analyze each question effectively, eliminate incorrect options, and select the best possible answer. In this section, we’ll cover strategies that can improve your chances of answering these types of questions correctly.

1. Read the Question Carefully: Begin by reading the question thoroughly before looking at the options. Understand what is being asked, and think about the concept involved. Sometimes, the question itself provides clues that make the correct answer more obvious.

2. Eliminate Clearly Wrong Answers: Once you’ve understood the question, immediately cross out the choices that are obviously incorrect. This reduces the number of options you have to consider and increases your chances of selecting the correct answer if you need to guess.

3. Look for Keywords and Clues: Pay attention to any keywords in the question or answer choices that could hint at the correct response. Words like “always,” “never,” “least,” or “most” often indicate important characteristics or conditions that can help you make an informed choice.

4. Consider All Options: Don’t settle for the first answer that seems right. Even if one option looks correct, read through the remaining choices to make sure another option doesn’t fit better. Sometimes the most accurate answer is the one that addresses every aspect of the question.

5. Use the Process of Elimination: If you’re unsure of the correct answer, use the process of elimination. Narrow down your choices by systematically ruling out options that don’t make sense, then make your best guess from the remaining answers.

By following these strategies, you can approach multiple-choice questions with more confidence and increase the likelihood of choosing the correct response. Remember, careful reading and thoughtful elimination are key to mastering this type of question.

Understanding Algebraic Equations and Expressions

Grasping the fundamentals of equations and expressions is essential for solving many types of mathematical problems. These mathematical structures are the foundation for most problem-solving techniques, and understanding them allows you to manipulate variables and constants effectively. In this section, we will explore the differences between expressions and equations, as well as how to work with them.

At the core of mathematics, an equation is a statement that asserts two expressions are equal, usually connected by an equal sign (=). On the other hand, an expression is a combination of numbers, variables, and operators without an equal sign, representing a value. The ability to work with both is crucial for mastering more advanced concepts.

Key Differences Between Equations and Expressions

Feature	Equation	Expression
Definition	A mathematical statement asserting equality between two expressions	A mathematical combination of numbers, variables, and operators without an equality
Contains	Equals sign (=)	No equals sign
Purpose	To solve for the value of a variable	To represent a value
Example	2x + 5 = 15	2x + 5

Understanding how to simplify and manipulate both equations and expressions is critical for solving mathematical problems. Equations often require finding the value of an unknown variable, while expressions can be simplified or evaluated for different values of the variables involved. Both skills are vital in approaching complex math tasks.

Working with Polynomials and Functions

Understanding how to work with polynomials and functions is crucial for solving many types of mathematical problems. These concepts form the backbone of many higher-level topics in mathematics, such as calculus and systems of equations. Polynomials, which are algebraic expressions involving sums of powers of variables, and functions, which define relationships between input and output values, are two foundational elements in mathematics.

A polynomial is an expression consisting of variables raised to non-negative integer powers, combined with coefficients. They can range from simple linear expressions to more complex forms with multiple terms. The degree of a polynomial is determined by the highest power of the variable in the expression. The ability to manipulate and simplify polynomials is essential for solving problems involving these types of expressions.

A function is a mathematical relationship that assigns exactly one output for each input. Functions are often represented by equations, tables, or graphs, and they can describe a wide range of phenomena. By understanding the behavior of functions, you can predict outputs, solve for unknown variables, and analyze trends in data.

Key Techniques for Working with Polynomials

Addition and Subtraction: Combine like terms to simplify the expression.
Multiplication: Use the distributive property or FOIL method for binomials.
Factoring: Break down a polynomial into simpler factors.
Division: Use long division or synthetic division to divide polynomials.

Working with Functions

Evaluating Functions: Substitute values for the variables and simplify to find the output.
Graphing Functions: Plot points on a coordinate plane to visualize the function’s behavior.
Solving Equations: Set the function equal to a value and solve for the variable.

By mastering the manipulation of polynomials and understanding the fundamental properties of functions, you can approach a wide variety of mathematical challenges with confidence and precision.

Preparing for Word Problems in Algebra

Word problems can be one of the most challenging aspects of any mathematical course. They require the ability to translate real-life situations into mathematical expressions and equations. This process involves understanding the problem’s context, identifying the relevant variables, and applying appropriate methods to solve for the unknowns. Mastering this skill not only enhances problem-solving abilities but also makes abstract concepts more tangible and easier to grasp.

The first step in solving word problems is to carefully read and analyze the information provided. Take note of any quantities, relationships, or conditions described in the problem. Often, it helps to highlight key terms or numbers that represent specific values. Once you’ve gathered the necessary information, you can proceed to define variables that will stand for the unknown quantities in the problem.

Next, translate the word problem into an equation. This step involves converting the verbal descriptions into mathematical expressions using variables and constants. Depending on the type of problem, the equation might involve addition, subtraction, multiplication, division, or more complex operations. The goal is to express the problem in a form that can be solved using algebraic techniques.

After formulating the equation, apply the relevant mathematical methods to solve for the unknown values. This might involve simplifying expressions, solving linear equations, or even using systems of equations when there are multiple unknowns. Once the solution is found, it is important to interpret the result in the context of the problem and check that it makes sense.

With practice, word problems become easier to tackle. By developing a step-by-step approach, you can build confidence and improve your ability to handle even the most complex real-world scenarios.

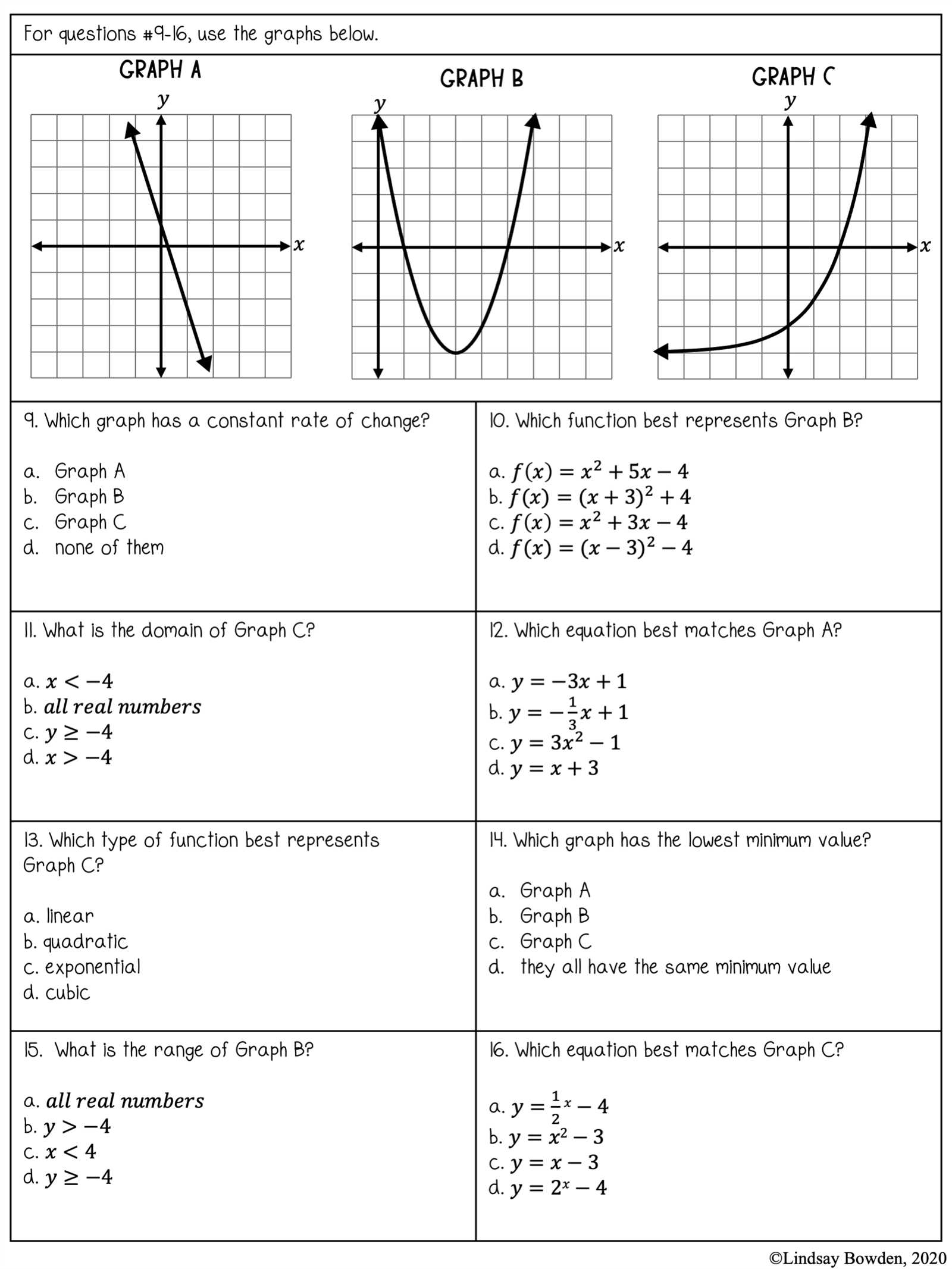
The Role of Graphs in the Final Exam

Graphs are powerful tools in mathematics that provide a visual representation of relationships between variables. In any assessment focused on mathematical concepts, understanding how to interpret and create graphs is crucial. They help to simplify complex equations and make abstract concepts more tangible. Whether it’s plotting a line, curve, or other forms of data, graphs serve as a bridge between algebraic expressions and their real-world applications.

Importance of Graphical Representation

In many mathematical problems, graphs allow you to visualize the solution and understand the behavior of equations. For instance, plotting a linear equation can help identify its slope and intercept, offering a clear view of its properties. Similarly, graphs can show how different variables interact, providing insight into trends, patterns, and relationships.

Tips for Interpreting Graphs

When approaching problems involving graphs, it’s important to pay attention to several key details:

Axes Labels: Always check the labels on the x-axis and y-axis to understand what each variable represents.
Scale: Ensure the scale is consistent and correctly interpreted. Misunderstanding the scale can lead to incorrect conclusions.
Key Points: Identify key points such as intercepts, maxima, or minima. These often represent important values in the problem.

By practicing graph interpretation and creation, students can build confidence and improve their ability to solve a variety of problems quickly and accurately.

Reviewing Past Assignments for Insights

One of the most effective ways to prepare for any assessment is to revisit previous assignments. These tasks often highlight the areas where you struggled or excelled, providing valuable insights into your understanding of key concepts. By carefully reviewing past work, you can identify patterns in mistakes, reinforce strengths, and refine strategies for approaching similar problems in the future.

Learning from Mistakes

Looking back at assignments where you made errors can be an eye-opening experience. It allows you to pinpoint where your understanding may have faltered and why. Common mistakes might include misinterpreting a problem, overlooking a small detail, or applying the wrong method. By analyzing these mistakes, you can work to avoid them in future problems. Take time to correct each error, and practice similar problems until you feel confident in your approach.

Reinforcing Key Concepts

Past assignments also serve as a great opportunity to reinforce important topics that may appear again. Revisit the problems that tested your knowledge of key ideas, such as solving equations, graphing functions, or working with expressions. By reviewing how you approached these tasks, you can strengthen your foundational knowledge and ensure that you fully understand the material. Regularly reviewing past work helps to solidify your grasp on essential concepts and builds confidence for future challenges.

Staying Calm During the Final Exam

When faced with a significant assessment, it’s natural to feel a bit anxious. However, maintaining a sense of calm can greatly improve your performance. Staying composed allows you to think more clearly, manage your time better, and approach each question with confidence. By developing strategies to handle stress, you can ensure that you are performing at your best, even under pressure.

Breathing Techniques for Relaxation

One of the simplest and most effective ways to calm yourself is through deep breathing exercises. By focusing on slow, deliberate breaths, you can reduce feelings of anxiety and regain mental clarity. Deep breathing helps to relax the body, slow down your heart rate, and reset your focus. Try taking a few deep breaths before starting the test, and whenever you feel overwhelmed during the process, pause for a moment to regain control.

Time Management and Focus

Effective time management is another key factor in staying calm. If you’re rushing through the questions, your stress levels will increase. Instead, set a reasonable pace from the start, and allocate time for each section. Make sure to avoid getting stuck on any one question for too long–move on and come back to it later if necessary. Prioritize your focus on completing the assessment efficiently, without rushing, to maintain a steady state of mind throughout the process.