
In this section, we explore essential principles related to shapes, their properties, and relationships that are fundamental for solving geometric challenges. Mastery of these ideas lays the groundwork for solving a wide range of problems effectively and with precision.
Critical thinking and problem-solving skills play an integral role in tackling complex visual and logical puzzles. By reviewing key concepts and practicing various techniques, you can improve your ability to approach and solve even the most challenging tasks.
From basic principles to advanced techniques, this guide will help you sharpen your understanding and ensure you are prepared to tackle any question that involves spatial reasoning and measurements. By the end, you will be better equipped to apply these principles in both academic and real-world contexts.
Geometry Chapter 8 Review Answers
In this section, we will break down key exercises and provide clear solutions to help you navigate through the most important concepts. Whether you’re solving for angles, understanding properties of figures, or working with spatial relationships, these step-by-step explanations will enhance your ability to tackle similar problems independently.
The following table presents common problems from this unit, along with detailed solutions to help clarify each step. By reviewing these examples, you can strengthen your understanding and apply these techniques to new challenges.
| Problem | Solution |
|---|---|
| Find the missing angle in a triangle | Subtract the known angles from 180° to find the unknown angle. |
| Determine the area of a rectangle | Multiply the length by the width (A = l × w). |
| Calculate the perimeter of a polygon | Add the lengths of all sides together (P = sum of sides). |
| Find the area of a circle | Use the formula A = πr², where r is the radius. |
| Identify the properties of a parallelogram | Opposite sides are equal, and opposite angles are congruent. |
Overview of Chapter 8 Concepts
This section introduces fundamental principles related to the properties of various shapes and their relationships. By focusing on the key ideas in this unit, we explore essential methods to calculate measurements, prove properties, and apply these concepts to more complex problems. Understanding these core ideas is crucial for tackling more advanced topics in spatial reasoning and mathematical problem-solving.
Throughout this part of the study, emphasis is placed on how different figures interact within the plane, from triangles to quadrilaterals. Students will also learn how to manipulate equations that describe these shapes and apply these techniques to real-world situations. The goal is to strengthen the ability to identify patterns and solve for unknowns efficiently using logical reasoning.
Key Theorems in Geometry Chapter 8
This section highlights the most important principles that govern relationships between various shapes and figures. These theorems form the foundation for solving numerous problems, allowing you to deduce unknown properties from given information. A deep understanding of these concepts is essential for progressing in mathematical reasoning and applying these principles in practical scenarios.
Below are some of the most critical theorems that are essential for mastering this material:
- Pythagorean Theorem: Describes the relationship between the sides of a right triangle, stating that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
- Angle Sum Theorem: States that the sum of the interior angles of any triangle is always 180°.
- Parallel Lines Theorem: If two lines are parallel, corresponding angles are congruent, and alternate interior angles are equal.
- Congruence Theorems: Criteria such as Side-Angle-Side (SAS) and Angle-Side-Angle (ASA) for determining when two triangles are congruent.
- Area Theorem for Polygons: Provides formulas for calculating the area of various polygons, such as rectangles, squares, and circles, based on their specific properties.
These theorems not only aid in solving theoretical problems but also serve as powerful tools for real-life applications such as architecture, design, and engineering. Understanding them thoroughly will significantly improve your ability to approach geometric tasks with confidence and precision.
Common Mistakes in Chapter 8 Review
As you work through problems in this section, there are several common errors that can hinder progress and lead to incorrect solutions. Identifying and understanding these mistakes is crucial to improving accuracy and mastering the material. Recognizing where things can go wrong will help avoid repeating these pitfalls in future exercises.
Misunderstanding properties of shapes: One common mistake is confusing the properties of similar figures, such as misapplying theorems about triangles or quadrilaterals. It’s important to carefully review the specific characteristics of each shape and apply the correct principles.
Incorrect use of formulas: Another frequent error involves using the wrong formula or misapplying a correct formula. For example, when calculating areas or perimeters, be sure you’re using the appropriate equation for the figure in question. Double-check whether the values provided match the necessary dimensions for the formula.
Overlooking angle relationships: Angles play a critical role in solving many problems. A common mistake is neglecting to account for the sum of angles in polygons or forgetting the properties of corresponding and alternate angles in parallel lines. Be sure to carefully examine all angle relationships in each problem.
Skipping steps in calculations: Rushing through calculations can lead to simple errors, such as incorrect arithmetic or missing terms. Always take the time to show your work and verify each step before moving to the next part of the problem.
Not double-checking answers: Finally, failing to review answers before concluding can result in overlooking minor errors. After completing a problem, take a few moments to review your solution, ensuring that every step aligns with the given information and that the final answer makes sense.
Step-by-Step Guide to Answering Questions
Approaching mathematical problems systematically can make even the most complex tasks more manageable. By breaking down each question into smaller, more manageable steps, you can ensure that you don’t overlook any important details and arrive at the correct solution. This methodical approach not only helps with accuracy but also builds confidence in your problem-solving abilities.
Step 1: Understand the problem: Before you begin solving, take a moment to read through the question carefully. Identify the known values, the unknowns, and what the problem is asking for. Clarifying these details will guide the next steps and ensure you are focused on what needs to be solved.
Step 2: Choose the right approach: Once you understand the problem, decide which method or formula is best suited for solving it. If you’re dealing with a figure, look for key properties such as symmetry, angles, or side lengths. If it’s an equation, determine which rules or theorems apply. Having a clear strategy will save time and help you stay organized.
Step 3: Set up the equation: Begin by translating the problem into a mathematical expression. This might involve writing down the relevant formula or equation, and ensuring that all the known variables are correctly substituted. Keep your work neat and organized to avoid confusion as you proceed.
Step 4: Solve step-by-step: Take your time to work through the equation or diagram one step at a time. Avoid rushing through the calculations. Solve for the unknowns, showing all intermediate steps along the way. If necessary, use a calculator for complex arithmetic, but double-check each step to ensure accuracy.
Step 5: Verify your solution: After solving the problem, double-check your final answer. Review your steps to ensure no mistakes were made during calculations. If possible, plug your answer back into the original problem to verify that it makes sense and meets the required conditions.
Understanding Geometric Proofs in Chapter 8
In this section, we explore the process of logically demonstrating the truth of various statements related to shapes and figures. Proofs are essential for establishing the validity of relationships, theorems, and properties within mathematical reasoning. By constructing a well-supported argument, you can justify the steps taken to reach a conclusion and ensure the accuracy of your solution.
To successfully understand and write a proof, it is important to follow a structured approach. Begin by identifying the given information and the desired result. Then, using known theorems and properties, step through each logical connection until the conclusion is reached. Each step must be justified with clear reasoning, ensuring that the proof is valid and coherent.
Through consistent practice, you will become more comfortable with the techniques used in writing proofs, such as direct reasoning, indirect proof, and the application of specific rules. This skill will not only help you in solving complex problems but also strengthen your ability to think critically and solve puzzles with precision.
How to Approach Review Exercises
When tackling exercises designed to reinforce key concepts, a methodical and organized approach is essential for success. These problems serve as an opportunity to apply what you’ve learned and identify areas where further understanding is needed. By following a clear strategy, you can work through each task more effectively and confidently.
Here are some steps to help guide you through the process:
- Read each problem carefully: Ensure you understand what is being asked before jumping into calculations. Pay attention to given information and what needs to be found.
- Identify key concepts: Look for relevant formulas, theorems, or principles that apply to the problem. Recognizing which techniques to use is crucial for efficiency.
- Break down the problem: Divide the problem into smaller parts. Tackle each section one step at a time to avoid feeling overwhelmed.
- Show your work: Write down each step, no matter how small. This will help you stay organized and catch any mistakes before finalizing your answer.
- Review your solution: Once you’ve reached a conclusion, double-check your work. Ensure that your solution makes sense and that no steps were skipped.
By following these steps, you will not only improve your ability to solve exercises but also gain a deeper understanding of the concepts involved. Practice and careful review will help solidify your knowledge and prepare you for more complex challenges ahead.
Real-Life Applications of Geometry Chapter 8
The concepts learned in this section extend far beyond the classroom, influencing various fields such as engineering, architecture, design, and even technology. Understanding how geometric principles apply to the real world is crucial for solving practical problems and making informed decisions in numerous professions. By mastering the skills in this unit, you can appreciate the significance of geometric thinking in shaping the world around us.
Applications in Architecture and Design
In fields like architecture and interior design, geometric principles are fundamental to creating efficient and aesthetically pleasing spaces. Professionals use various properties of shapes, angles, and proportions to calculate dimensions, design layouts, and ensure structural integrity.
| Application | Description |
|---|---|
| Blueprints and Floor Plans | Architects use geometric shapes to design building layouts, ensuring proper space utilization and structural support. |
| Structural Engineering | Engineers apply geometric concepts to determine load-bearing walls, angles, and the overall stability of structures. |
| Interior Design | Designers use proportions and symmetry to create balanced and visually appealing rooms and spaces. |
Applications in Technology and Manufacturing
In technology and manufacturing, geometry is used to design products, create prototypes, and develop machines with precision. Computer-aided design (CAD) software, for instance, relies heavily on geometric principles to model 3D objects and simulate real-world behavior.
| Application | Description |
|---|---|
| 3D Modeling | CAD software uses geometric algorithms to create digital models of objects for prototyping and production. |
| Manufacturing Processes | Geometry helps engineers plan cutting patterns, assembly lines, and optimize material usage in production. |
| Robotics | Robots rely on geometric calculations to navigate spaces, pick up objects, and perform precise tasks. |
By understanding the importance of geometric concepts in these real-world applications, students can better appreciate the value of this knowledge and how it directly impacts daily life and various industries.
Tips for Solving Complex Problems
When faced with intricate challenges, it is essential to approach the problem methodically. Complex tasks can seem daunting at first, but breaking them down into manageable steps and applying logical strategies can make them more approachable. Developing problem-solving skills takes time and practice, but using specific techniques can significantly improve your efficiency and accuracy.
Break Down the Problem
The first step in solving a complicated issue is to deconstruct it. Identify the key elements and separate them into smaller, more digestible parts. By focusing on one piece at a time, you can avoid feeling overwhelmed and reduce the risk of missing important details.
Start by reviewing the information provided and what needs to be found. Organize known facts, variables, and relationships in a way that makes sense. This may involve drawing diagrams, creating lists, or writing out equations. Once the problem is simplified, proceed with each step logically.
Use Logical Reasoning and Patterns
Often, complex problems require recognizing patterns and applying appropriate reasoning. Look for trends in the numbers, shapes, or relationships within the problem that could guide you to the solution. This involves utilizing any known theorems or rules that are relevant to the situation.
Try to foresee the possible outcomes as you work through each step, and check for consistency at each stage. Be patient–sometimes solving a problem requires backtracking or adjusting your approach if something doesn’t align as expected. Keep refining your strategy until you reach the correct conclusion.
By following these methods, you can break down complex problems into simpler tasks, applying logic and reasoning to navigate through them efficiently. With practice, tackling difficult questions will become a more manageable and rewarding experience.
Explanation of Key Diagrams and Figures
In many problems, visual aids such as diagrams and figures play a crucial role in understanding the relationships between different elements. These visuals help clarify complex concepts and allow you to better visualize how the various components interact with each other. Properly interpreting these representations is key to solving problems accurately and efficiently.
Here are some common types of diagrams and their importance:
- Shapes and Figures: Diagrams featuring polygons, circles, or other geometric forms provide a clear view of their properties, such as angles, sides, and symmetries. Recognizing these features helps in applying relevant formulas and theorems.
- Angle Representations: Diagrams that display angles between lines or planes are essential for understanding geometric relationships. These visuals are used to calculate unknown angles or prove certain angle properties.
- Coordinate Grids: When problems involve points, lines, or curves on a plane, coordinate grids offer a way to plot and analyze these elements systematically. Understanding how to navigate these grids can make solving problems with coordinates or distances much simpler.
- Vectors and Arrows: Arrows or vector diagrams show direction and magnitude, which are vital when dealing with transformations or motions in a space. Interpreting these diagrams correctly allows you to solve problems involving displacement, velocity, and other related concepts.
To make the most of these visual aids, it’s essential to focus on the following:
- Labeling: Ensure that all key points, lines, and angles are clearly labeled. This helps prevent confusion and allows you to track the relationships between different components.
- Scale and Proportion: Pay attention to the scale of the diagram, especially in cases where precision is necessary. Some diagrams may be drawn to scale, while others may not, so be mindful of any given information about size or proportion.
- Relationship Identification: Look for any direct relationships, such as parallel lines, perpendicular angles, or congruent sides. Recognizing these connections can guide you toward applying the correct concepts and formulas.
By practicing the interpretation of key diagrams and figures, you’ll develop a deeper understanding of the subject and improve your ability to solve related problems more efficiently.
Strategies for Improving Accuracy
Achieving high precision in solving mathematical problems requires careful attention to detail and the application of systematic techniques. Whether you’re working with numbers, shapes, or logical relationships, taking steps to minimize errors can significantly enhance your problem-solving skills. Below are several strategies that can help improve accuracy when tackling complex tasks.
Double-Check Calculations and Work
One of the most effective methods for improving accuracy is consistently reviewing your work. Errors often occur during calculations or while interpreting problem statements. Double-checking every step ensures that you haven’t missed any important details or made simple arithmetic mistakes.
- Rework key steps: If you’re uncertain about a particular result, go back to the original step and re-calculate. This can help identify where things went wrong.
- Check for consistency: Compare your results with expected patterns or known values. For example, if you’re solving for angles, verify that they add up to the correct total based on known geometric principles.
- Use estimation: Before diving into lengthy calculations, estimate the possible range for your answer. This can help spot glaring mistakes when the actual result is far off from your estimate.
Organize Your Work Clearly
Maintaining a clear and organized approach helps reduce the likelihood of mistakes. Keeping your thoughts and work properly arranged will allow you to focus on the important details and catch any discrepancies more easily.
- Label all variables: Assign labels to key elements, such as points, lines, or angles, to make it easier to follow your work. Clear labeling prevents confusion when dealing with multiple components.
- Use logical steps: Write out every part of your solution process. Avoid skipping steps, as this can lead to missing essential information. Having a clear sequence helps you stay focused and minimizes oversight.
- Use diagrams: Whenever possible, draw diagrams to help visualize the problem. This can help you confirm relationships between different elements and clarify how you’re approaching the solution.
By integrating these strategies into your practice, you can increase the precision of your results, reduce mistakes, and improve your overall problem-solving abilities.
Using Online Tools for Geometry Practice
In the digital age, there are numerous online platforms available that can help enhance your understanding and proficiency in solving spatial and mathematical problems. These tools offer a range of features, from interactive problem-solving exercises to instant feedback, which can significantly accelerate the learning process. Utilizing these resources can make practice more engaging and effective.
Here are some key advantages of using online tools for practice:
- Interactive Exercises: Many websites provide interactive quizzes and exercises that allow you to apply what you’ve learned in a hands-on way. These platforms often offer various difficulty levels, so you can gradually increase the challenge as you improve.
- Instant Feedback: Online tools typically give immediate feedback, allowing you to understand any mistakes right away. This helps reinforce the correct concepts and improves your accuracy over time.
- Visual Aids and Simulations: Visual learning tools, such as interactive diagrams and 3D models, can help you better understand complex relationships and geometrical properties, especially when dealing with shapes and spatial reasoning.
- Accessible Anywhere: Many online tools are available across devices, meaning you can practice at any time and from any location, making learning more flexible and convenient.
Some of the most useful online tools for mathematical practice include:
- Interactive Graphing Calculators: These tools allow you to visualize equations, graph lines, and explore relationships between variables, making them useful for understanding coordinate-based problems.
- Problem Solving Websites: Websites that specialize in offering problems, solutions, and detailed explanations for various types of mathematical exercises can guide you through step-by-step processes and demonstrate correct techniques.
- Online Forums and Communities: Engaging with other learners and experts in online discussion forums can be an invaluable way to gain new insights, clarify doubts, and get advice on tackling tricky problems.
By incorporating online resources into your study routine, you can enhance your skills, track your progress, and better prepare for challenges, ultimately improving your overall performance.
Practice Questions and Solutions
Engaging with practice questions is an essential part of mastering any subject. By applying learned concepts to different problems, you can deepen your understanding and identify areas that need further improvement. Below, you’ll find a collection of practice questions along with their detailed solutions to guide you through various problem-solving methods.
Sample Problem 1
Question: Calculate the area of a triangle with a base of 10 units and a height of 5 units.
Solution: The area of a triangle is given by the formula:
Area = (Base × Height) / 2
Substitute the given values:
Area = (10 × 5) / 2 = 50 / 2 = 25
The area of the triangle is 25 square units.
Sample Problem 2
Question: Find the value of angle x in a triangle where the other two angles are 45° and 85°.
Solution: The sum of the angles in any triangle is always 180°. Therefore, to find angle x, subtract the sum of the known angles from 180°:
x = 180° – (45° + 85°)
x = 180° – 130° = 50°
The value of angle x is 50°.
By practicing these types of questions and reviewing the solutions, you can build confidence in applying concepts and enhance your problem-solving skills.
Common Formulas in Chapter 8
In this section, we will cover a set of fundamental formulas that are essential for solving various problems related to shapes, sizes, and their properties. Mastering these formulas is key to successfully solving complex questions and improving your mathematical understanding. Below are the most commonly used formulas that will aid in solving typical exercises.
Area Formulas
The area of different shapes is a critical concept to grasp. Here are some common area formulas:
- Rectangle: Area = Length × Width
- Triangle: Area = (Base × Height) / 2
- Circle: Area = π × Radius²
- Parallelogram: Area = Base × Height
Perimeter Formulas
Perimeter refers to the total length around a shape. Here are the formulas for calculating perimeter:
- Rectangle: Perimeter = 2 × (Length + Width)
- Square: Perimeter = 4 × Side
- Triangle: Perimeter = Side₁ + Side₂ + Side₃
- Circle (Circumference): Perimeter = 2 × π × Radius
Familiarizing yourself with these basic formulas will allow you to quickly solve a wide range of problems involving geometric figures and their measurements.
Tips for Time Management During Tests
Effective time management is crucial during any exam, as it ensures you can address all the questions without feeling rushed. With the right strategies, you can optimize your time and improve your performance. Below are some tips that can help you make the most of your allotted time.
First, it is important to understand the structure of the test. Allocate specific time slots to each section based on its difficulty and the number of points it carries. This will help you avoid spending too much time on a single question and allow you to answer everything within the time limit.
Strategies for Efficient Time Allocation
| Action | Time Allocation | Tip |
|---|---|---|
| Quick Overview | 5-10 minutes | Skim through all the questions to get an idea of their difficulty. |
| Answer Easy Questions | 25-30 minutes | Start with the questions you find easiest to build confidence and save time. |
| Work on Challenging Questions | 45-50 minutes | Focus on difficult questions, but don’t get stuck. Move on if you’re unsure. |
| Review and Double-Check | 10-15 minutes | Leave time at the end to review your answers for mistakes. |
By planning ahead and managing your time wisely, you will not only reduce test anxiety but also increase your chances of completing all questions accurately.
Resources for Additional Study
When preparing for exams or seeking to strengthen your understanding, utilizing various resources can make a significant difference. From online platforms to books, having access to high-quality study materials can enhance your grasp of complex concepts. Below are several valuable tools and sources to consider for further practice and learning.
Online Learning Platforms
- Khan Academy – A comprehensive educational site offering video tutorials and practice exercises for a wide range of subjects.
- Coursera – Provides in-depth courses from top universities and institutions, perfect for learners who want more structured content.
- Wolfram Alpha – An advanced computational engine that helps solve problems and explain concepts step-by-step.
Books and Study Guides
- “The Art of Problem Solving” – A series of books designed to challenge and improve problem-solving skills, especially for mathematics enthusiasts.
- “Schaum’s Outlines” – A great collection of problem sets and solutions for self-study, covering a variety of topics and skill levels.
- “Barron’s Test Prep” – Offers study guides tailored to various exams, with clear explanations and extensive practice problems.
Using these resources in combination with regular practice can significantly improve both your confidence and performance. Whether you prefer interactive online platforms or comprehensive textbooks, each tool provides unique benefits to suit different learning styles.
Reviewing Key Vocabulary
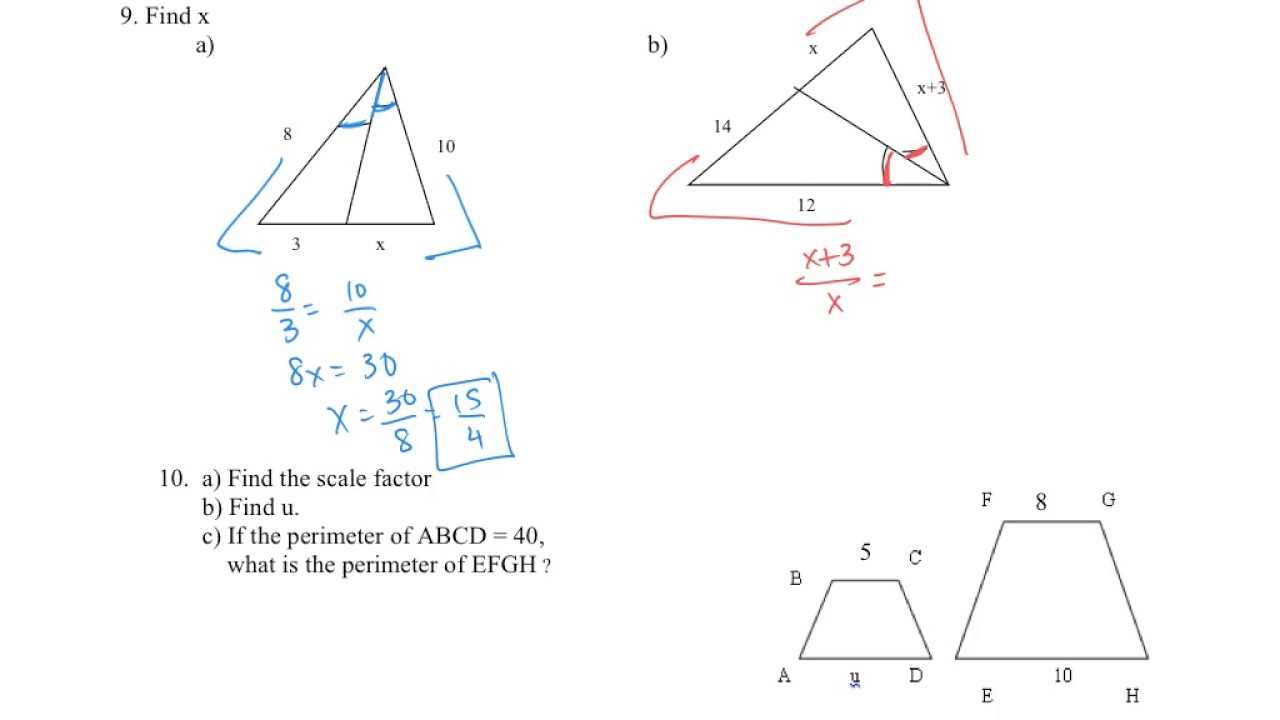
Understanding the terminology used in mathematical contexts is crucial for solving problems efficiently and accurately. Each term represents a fundamental concept that helps build a deeper understanding of the subject. This section focuses on important terms and definitions that are essential to mastering the material. Familiarizing yourself with these words will not only enhance your problem-solving skills but also help you communicate complex ideas more clearly.
The table below lists key terms and their definitions that are frequently encountered in exercises and proofs. Reviewing these terms will help ensure that you are comfortable with the concepts they represent and ready to apply them effectively in various scenarios.
| Term | Definition |
|---|---|
| Angle | The space between two intersecting lines measured in degrees. |
| Parallel Lines | Two lines that never intersect and are always equidistant. |
| Perpendicular | Two lines that intersect at a 90-degree angle. |
| Congruent | Figures or shapes that are identical in size and shape. |
| Radius | The distance from the center of a circle to any point on its circumference. |
| Diameter | The straight line passing through the center of a circle, connecting two points on its boundary. |
| Area | The total surface space enclosed by a shape or figure. |
| Volume | The amount of space occupied by a three-dimensional object. |
By reviewing these essential terms, you will be better prepared to understand more complex concepts and solve problems with greater ease. Regular practice with these definitions will reinforce your understanding and ensure a solid foundation for tackling various mathematical challenges.
How to Prepare for the Exam
Successfully preparing for an upcoming test requires a structured approach that covers all necessary topics while focusing on understanding key concepts. Rather than cramming at the last minute, it’s essential to build a study plan that gives you adequate time to review the material, practice problems, and refine your skills. The following tips will help you approach your preparation with confidence and efficiency.
1. Understand the Key Concepts
Start by revisiting the main ideas and theorems covered in your lessons. Be sure you understand the foundational principles, as these will serve as the building blocks for solving more complex problems. Pay particular attention to definitions, properties, and formulas. These are critical for both multiple-choice questions and more detailed, application-based problems.
2. Practice with Sample Problems
Consistent practice is one of the best ways to solidify your understanding and improve problem-solving speed. Work through a variety of practice problems, especially those you find challenging. This will help you identify areas where you might need additional review. If you’re unsure about the steps, seek explanations from textbooks, online resources, or peers.
3. Review Mistakes and Correct Them
After practicing, review the problems you’ve gotten wrong. Focus on understanding where you made mistakes and the correct methods for solving those problems. This step will help you avoid repeating the same errors on the exam and increase your overall accuracy.
4. Use Resources Wisely
In addition to textbooks, make use of online tutorials, videos, and practice exams. These resources often present the material in different ways, which can enhance your understanding. Consider using study groups where you can discuss difficult topics and test each other’s knowledge.
5. Manage Your Time
During your study sessions, allocate enough time for each topic, and avoid spending too long on any one area. Create a schedule leading up to the exam, ensuring that you cover everything without rushing. Time management will allow you to feel calm and confident on exam day.
By following these strategies, you’ll be well-prepared and ready to tackle the test with greater ease and understanding.