Algebra Nation Answers Section 7 Complete Guide

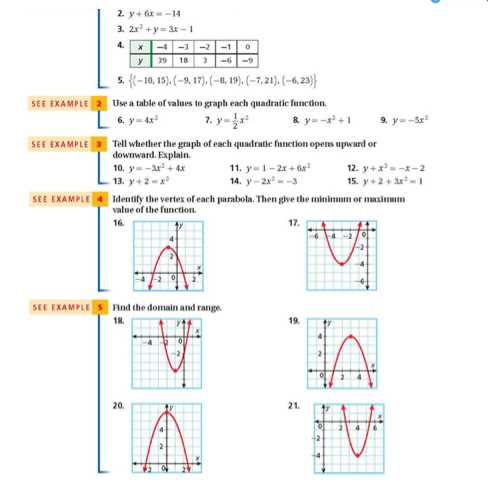
In this section, we focus on understanding and solving some of the most challenging problems that require logical thinking and mathematical skills. By breaking down complex scenarios into manageable steps, students can gain a clearer perspective on how to approach and solve them efficiently.

Whether you’re tackling advanced equations or working through word problems, the key to success lies in knowing how to apply the right methods and formulas. With the right techniques, even the most difficult tasks become more manageable, leading to better performance and deeper comprehension of the material.

Effective practice and understanding the core principles behind each problem are essential. This guide will provide the tools and insights you need to approach the material with confidence, enhancing both your problem-solving speed and accuracy.

Algebra Nation Section 7 Overview

This part of the course delves into essential concepts and problem-solving strategies that form the foundation of higher-level mathematics. It is designed to help learners build a strong understanding of complex topics by simplifying the approach and offering practical solutions. The focus is on mastering the techniques necessary to work through challenging exercises efficiently and accurately.

The section covers a variety of topics, each with its own set of principles and methods. By focusing on key areas, students can apply these strategies to a broad range of mathematical problems, improving both their skills and their confidence in handling new material. Below is an overview of the core subjects explored in this part of the curriculum:

Topic	Description
Linear Equations	Methods for solving equations involving variables and constants.
Systems of Equations	Techniques for solving sets of equations with multiple variables.
Inequalities	Understanding and solving problems involving greater-than or less-than relationships.
Graphing Techniques	How to plot and interpret functions on a coordinate plane.
Factoring	Breaking down complex expressions into simpler components.

Key Concepts in Section 7

This portion of the curriculum focuses on critical mathematical principles that help learners solve a wide range of problems. The primary goal is to build a deeper understanding of how to manipulate and apply these ideas effectively. Mastering these concepts not only improves problem-solving ability but also enhances the overall approach to learning more advanced topics.

Understanding Variables and Equations

At the core of this section is a strong emphasis on working with variables and formulating equations. Being able to recognize the structure of an equation and apply appropriate methods to isolate variables is a crucial skill. This includes:

Identifying and understanding terms and coefficients.
Applying operations to simplify and solve equations.
Recognizing different types of equations and how to approach them.

Solving for Unknowns

The ability to solve for unknown values is fundamental to mastering mathematical challenges. This process often involves:

Using substitution and elimination techniques for solving systems of equations.
Working through inequalities and understanding their properties.
Graphing solutions on coordinate planes for visual understanding.

By honing these skills, learners develop a well-rounded approach to problem-solving, allowing them to tackle more complex tasks with confidence.

Understanding the Main Problems

In this part of the curriculum, the focus is on identifying and solving the most common types of problems that students encounter. A strong grasp of these core challenges is essential for developing the skills needed to approach more advanced material. By breaking down these problems into clear steps, learners can improve their ability to solve complex issues with accuracy and confidence.

Identifying Problem Types

Each problem presents unique characteristics that require specific methods to solve. Recognizing the type of problem at hand helps determine the appropriate approach. Key aspects include:

Understanding whether the problem is an equation, inequality, or word problem.
Recognizing patterns in the numbers and variables provided.
Choosing the right mathematical operations to simplify and solve the problem.

Breaking Down Complex Problems

Once a problem is identified, it’s important to deconstruct it into smaller, manageable parts. This process helps prevent confusion and allows for more effective solutions. Steps involved are:

Writing out all given information clearly.
Isolating unknowns and focusing on relationships between terms.
Applying the correct sequence of operations to simplify and solve.

By mastering the ability to analyze and break down problems, students can tackle even the most challenging exercises with greater ease.

Step-by-Step Solutions for Section 7

In this part of the guide, we will break down the most challenging problems into simple, manageable steps. Understanding the process of solving each type of problem is essential for building confidence and ensuring accuracy. By following these step-by-step instructions, learners can systematically approach even the most complex exercises with clarity and precision.

Solving Linear Equations

Linear equations often appear straightforward but require careful attention to detail. Here’s how to tackle them:

Step 1: Identify the variables and constants within the equation.
Step 2: Simplify both sides of the equation, if necessary.
Step 3: Isolate the variable by applying inverse operations.
Step 4: Solve for the variable and check the solution.

By following these steps, you’ll be able to confidently solve any linear equation and verify your result with ease.

Solving Systems of Equations

Systems of equations involve finding values for multiple variables that satisfy all equations simultaneously. To solve these:

Step 1: Choose a method: substitution or elimination.
Step 2: For substitution, solve one equation for one variable, then substitute into the other equation. For elimination, add or subtract equations to eliminate one variable.
Step 3: Solve the resulting single-variable equation.
Step 4: Substitute the solution back into one of the original equations to find the second variable.

By practicing these methods, you’ll gain the ability to solve complex systems and approach them systematically with confidence.

Common Mistakes to Avoid

When solving mathematical problems, certain errors can easily lead to incorrect answers and misunderstandings. Recognizing and avoiding these common pitfalls is crucial for improving problem-solving skills and achieving more accurate results. By being aware of these mistakes, learners can enhance their ability to approach tasks more effectively and with confidence.

Incorrect Operations

One of the most frequent mistakes occurs when incorrect operations are applied during problem-solving. This often leads to errors in results and affects the overall process. Some common issues include:

Misapplying addition or subtraction when dealing with negative numbers.
Incorrectly multiplying or dividing terms with exponents.
Failing to distribute terms correctly in expressions.

Misunderstanding Equations and Inequalities

Another area where students often struggle is understanding the subtle differences between equations and inequalities. Key mistakes in this area include:

Ignoring the need to reverse the inequality sign when multiplying or dividing by a negative number.
Forgetting to check for extraneous solutions when solving equations with square roots or fractions.
Confusing the process of solving linear equations with that of solving quadratic ones.

By staying mindful of these common mistakes, learners can improve their accuracy and efficiency when tackling challenging mathematical problems.

Tips for Mastering Algebraic Techniques

Mastering key mathematical techniques is essential for solving complex problems with ease. To enhance your understanding and efficiency, it’s important to practice regularly and refine your approach. By focusing on the following strategies, you can improve your skills and tackle even the most challenging exercises with confidence.

Focus on Fundamentals

A strong grasp of basic principles is the foundation for solving more advanced problems. Here are some essential tips to reinforce the basics:

Review the rules for operations, such as distributive, associative, and commutative properties.
Ensure a deep understanding of working with variables and constants before moving on to more complex topics.
Strengthen your ability to simplify expressions and solve for unknowns through practice.

Practice Consistently

Like any skill, proficiency in mathematics comes with regular practice. The more problems you solve, the more comfortable you become with applying techniques. Consider the following tips to enhance your practice sessions:

Work on a variety of problems to expose yourself to different types of challenges.
Start with simpler problems to build confidence and gradually move on to more complex ones.
Keep a practice log to track your progress and identify areas for improvement.

Use Visual Tools

Many problems can be made easier to understand with the use of visual aids. These tools help clarify relationships between terms and offer a more intuitive approach to problem-solving:

Graph functions to visualize the relationships between variables.
Use diagrams or number lines to understand inequalities and systems of equations.
Leverage online graphing tools to help you visualize complex expressions.

By incorporating these techniques into your study routine, you’ll be able to solve problems more efficiently and with greater confidence.

How to Approach Word Problems

Word problems can often seem daunting because they require translating real-world scenarios into mathematical expressions. However, with the right approach, these types of problems become much more manageable. Breaking them down step by step and carefully analyzing the information provided is key to finding the solution. By following a structured method, you can turn any word problem into a solvable equation.

Understand the Problem

The first step in solving a word problem is to fully understand what is being asked. Focus on the key details and ignore any unnecessary information. Here’s how to get started:

Read carefully: Read the problem at least twice to ensure you understand the context and the question being asked.
Highlight key information: Identify the numbers, variables, and relationships in the problem. This helps in setting up your equation.
Identify what is unknown: Determine what you’re solving for, whether it’s a value, a rate, or a quantity.

Translate Words into Equations

Once you understand the problem, the next step is to translate it into a mathematical form. This requires recognizing the relationships between the elements of the problem and expressing them algebraically. Some tips include:

Look for keywords: Words like “total,” “difference,” “sum,” or “product” often correspond to specific mathematical operations.
Define variables: Assign letters (like x or y) to represent the unknown quantities.
Write an equation: Use the information from the problem to form an equation that represents the relationships between the quantities.

By following these steps, you can confidently approach any word problem and solve it step by step, ensuring that no important details are overlooked.

Real-World Applications of Algebra

The principles of solving equations and manipulating variables are not only useful in the classroom but also have a wide range of practical applications in everyday life. From budgeting to engineering, the skills learned in mathematical problem-solving are essential tools in many professions and real-world situations. Understanding how these concepts apply to various fields can help students appreciate the value of learning these techniques beyond academic exercises.

Finance and Budgeting

One of the most common uses of mathematical concepts is in managing personal finances. By setting up equations to track income, expenses, and savings, individuals can make informed decisions about their money. Key applications include:

Calculating loan payments: Using equations to determine monthly payments based on loan amount, interest rates, and term length.
Creating budgets: Setting up formulas to ensure income and expenses are balanced and that savings goals are met.
Investment growth: Using exponential growth formulas to predict the future value of investments or savings over time.

Engineering and Architecture

In fields like engineering and architecture, mathematical techniques are essential for designing structures and ensuring their stability. Applications include:

Structural design: Calculating load-bearing capacity, material strengths, and dimensions for safe and cost-effective construction.
Cost estimation: Estimating the amount of materials needed for a project and calculating overall project costs.
Optimization: Using equations to optimize resources, such as minimizing material waste while maintaining structural integrity.

Science and Medicine

In scientific research and medicine, mathematics plays a vital role in analyzing data and solving problems. Some areas where mathematical techniques are applied include:

Drug dosage calculations: Determining the appropriate amount of medication for patients based on factors like weight and age.
Statistical analysis: Analyzing research data to draw conclusions or predict outcomes in clinical studies.
Modeling natural phenomena: Using equations to simulate environmental systems, biological processes, or chemical reactions.

Understanding how abstract concepts translate into real-world solutions helps demonstrate the true power of problem-solving skills in practical settings.

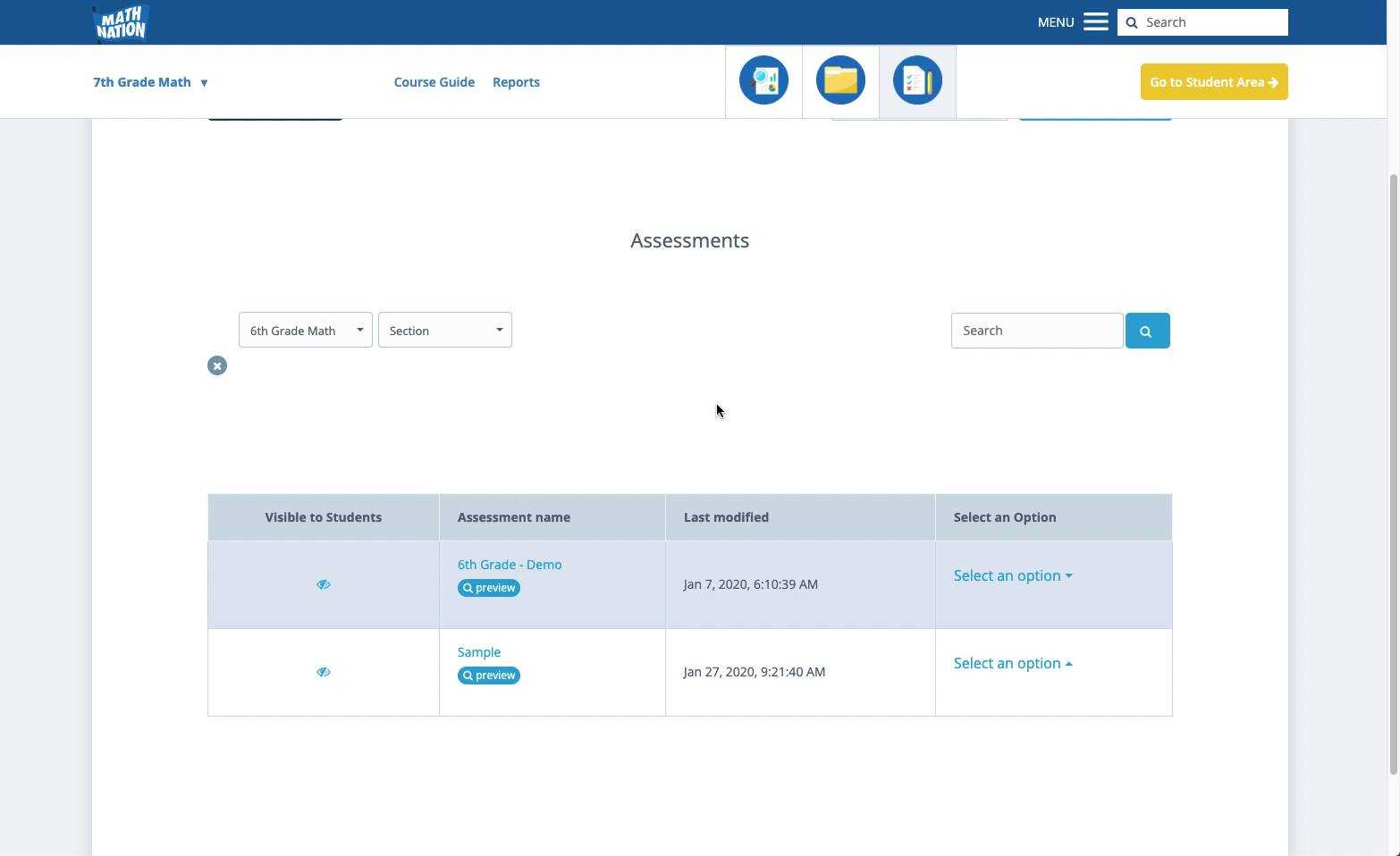
Tools to Help Solve Section 7 Problems

When tackling complex mathematical problems, having the right tools can make a significant difference in efficiency and accuracy. Whether you’re solving equations, analyzing data, or graphing functions, various resources and methods can aid in breaking down and solving problems more effectively. By utilizing these tools, you can gain a deeper understanding of the concepts and improve problem-solving skills.

Graphing Calculators

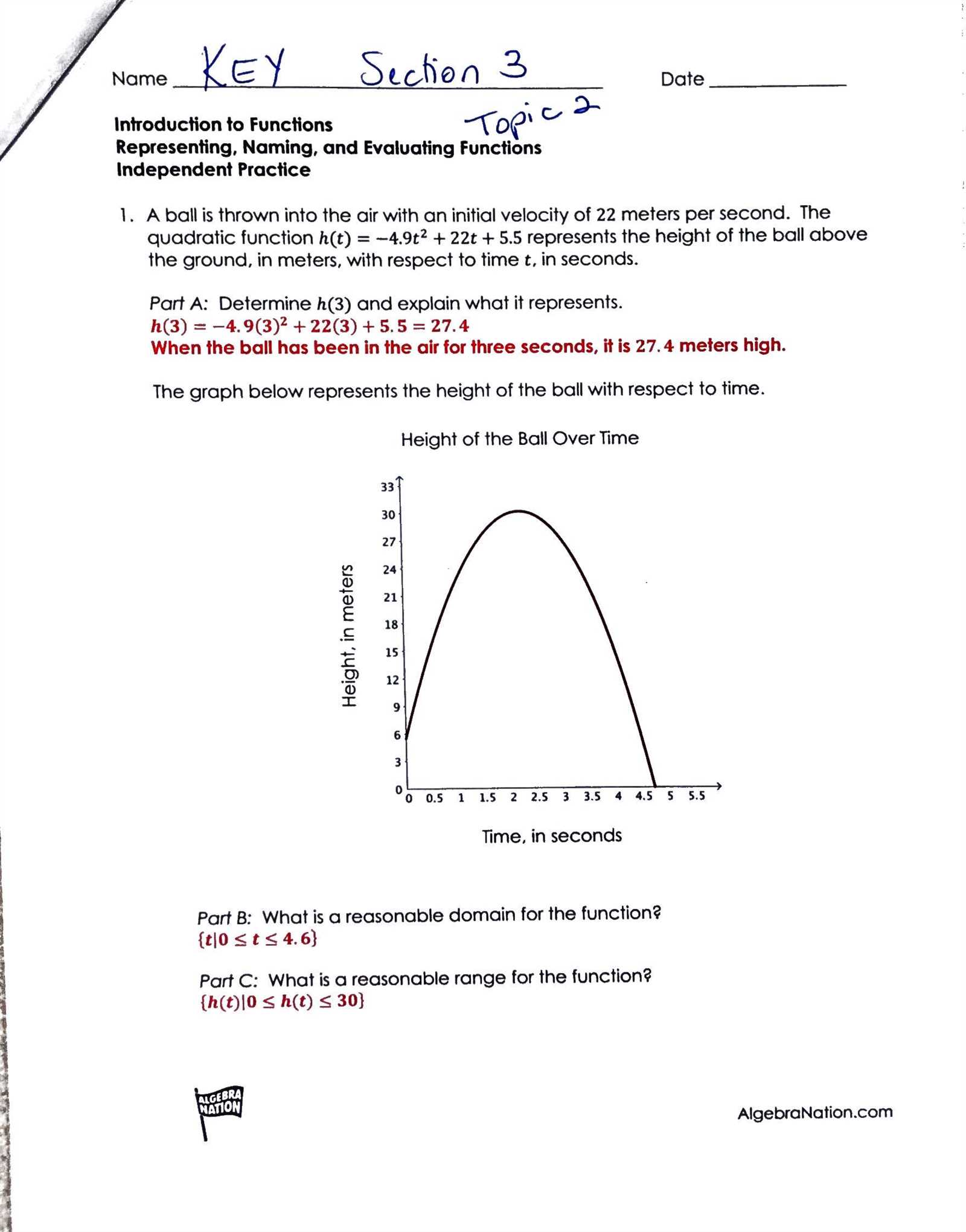
Graphing calculators are indispensable tools for visualizing equations and understanding the relationships between variables. They allow you to:

Plot functions: Quickly graph functions to observe their behavior and identify key features such as intercepts and asymptotes.
Perform calculations: Solve equations, compute derivatives, and perform integrals directly on the device.
Analyze data: Use built-in statistical functions to analyze data sets and perform regression analysis.

Online Math Solvers

In addition to physical calculators, online math solvers provide immediate assistance for solving various types of problems. These tools are convenient for quick answers and step-by-step solutions. Benefits include:

Instant solutions: Input a problem and get an immediate solution with detailed steps to understand the solution process.
Variety of functions: Solve equations, factor expressions, and perform matrix operations, among others.
Interactive features: Some solvers offer interactive elements, allowing you to adjust parameters and instantly see the effects on the solution.

Mathematical Software

For more advanced problem-solving, mathematical software like MATLAB, Wolfram Mathematica, or GeoGebra can help with detailed analysis. These platforms provide tools for:

Symbolic computation: Solve algebraic expressions symbolically, manipulate polynomials, and factor complex expressions.
Graphical representation: Visualize complex functions in multiple dimensions, enabling a better understanding of the problem.
Simulations and modeling: Use software to model real-world scenarios and simulate various mathematical processes.

By incorporating these tools into your problem-solving routine, you can not only simplify complex tasks but also deepen your understanding of mathematical concepts.

Breaking Down Complex Equations

When faced with a complex equation, it can be overwhelming to know where to start. However, by breaking the problem down into smaller, more manageable steps, solving even the most complicated expressions becomes much easier. By isolating individual components and simplifying one piece at a time, you can approach any problem systematically and with confidence.

Identify the Key Components

The first step in solving a complex equation is to identify its key components. Look for variables, constants, and any operations that need to be performed. Start by:

Recognizing terms: Identify the different terms in the equation, such as coefficients, constants, and variables.
Simplifying expressions: Combine like terms and simplify fractions or expressions wherever possible.
Recognizing operations: Determine which mathematical operations (addition, subtraction, multiplication, division) are involved in the equation.

Apply Step-by-Step Strategies

Once the components are identified, apply step-by-step strategies to solve the equation. Some key techniques include:

Isolate the variable: Move all terms with the variable to one side of the equation and constants to the other side.
Use inverse operations: Apply inverse operations (such as subtracting or dividing) to simplify each part of the equation.
Check for extraneous solutions: After solving, substitute the solution back into the original equation to ensure it is valid.

By following these structured steps, complex equations become far less intimidating. With practice, you’ll be able to solve them with ease, gaining confidence in your mathematical skills.

Strategies for Efficient Problem Solving

To solve problems effectively, it’s essential to develop a systematic approach that minimizes errors and maximizes efficiency. By applying certain strategies, you can streamline the process, reducing the time spent on each problem while improving accuracy. These methods focus on simplifying complex tasks, organizing information, and applying logical steps to reach the correct solution.

Organize and Simplify the Problem

Before diving into calculations, take a moment to organize the given information. Start by breaking down the problem into smaller, more manageable parts. Identifying the key components and their relationships helps to simplify the process. Here are some approaches:

Highlight important information: Identify known values and what you need to find.
Remove unnecessary details: Focus on the core elements that will lead to the solution.
Rearrange the problem: If possible, rewrite the problem in a simpler form to make it easier to understand.

Use Logical Steps and Patterns

Applying logical steps is crucial to solving problems efficiently. Recognizing patterns and knowing which techniques to apply can save time and reduce mistakes. Consider these strategies:

Apply known formulas: Use established mathematical formulas to simplify complex problems.
Look for patterns: Spot repeating elements in the problem to anticipate solutions.
Work backwards: Start with the desired outcome and trace back to find the required steps.

Use Tools and Resources

Leveraging tools such as calculators, software, or online resources can also enhance efficiency. Here are a few tools that can aid problem solving:

Tool	Benefit
Graphing Calculators	Visualize equations and identify solutions quickly
Mathematical Software	Perform complex computations and simulations
Online Solvers	Provide step-by-step solutions for various problems

By incorporating these strategies into your problem-solving process, you’ll be able to approach challenges with confidence, ensuring both speed and accuracy in your solutions.

Explaining Key Formulas in Section 7

Understanding the core formulas involved in solving mathematical problems is crucial for achieving accurate results. These essential equations provide the foundation for approaching a wide range of problems. By mastering these formulas, you can approach each problem with confidence, knowing exactly which principles to apply and how to manipulate them effectively.

Formula for Solving Linear Equations

Linear equations are often the starting point for many types of problems. The general formula for a linear equation is:

Ax + B = C

Where:

A represents the coefficient of the variable,
x is the unknown variable,
B is the constant,
C is the result after performing operations on the left side.

To solve for x, isolate it by performing inverse operations on both sides of the equation. For example, subtract B from both sides and then divide by A.

Quadratic Formula

The quadratic formula is another fundamental tool used to solve second-degree equations. The standard form of a quadratic equation is:

Ax² + Bx + C = 0

To solve for x, use the quadratic formula:

x = (-B ± √(B² – 4AC)) / 2A

Here:

A, B, and C are the coefficients of the equation,
The expression √(B² – 4AC) is known as the discriminant, which determines the nature of the solutions (real or complex).

By applying this formula, you can find the two possible values for x in quadratic problems, depending on the discriminant.

Improving Speed in Algebraic Solutions

Efficiency in solving mathematical problems is an essential skill that can greatly improve performance, especially when dealing with complex problems or time-sensitive tasks. By mastering a few key techniques and strategies, you can drastically increase your speed without sacrificing accuracy. The goal is to streamline your approach, making it easier to identify patterns, apply formulas quickly, and reduce unnecessary steps in your calculations.

Key Strategies for Speed

Understand the Problem: Before jumping into calculations, take a moment to fully comprehend the question and identify the key components. This can help avoid mistakes and save time in the long run.
Practice Mental Math: Developing your mental arithmetic skills allows you to perform simple operations quickly, without relying on a calculator or writing everything down.
Recognize Patterns: Identifying common structures in problems, such as common formulas or sequences, helps reduce the need to solve every problem from scratch.
Use Shortcuts: Learn and apply shortcuts for frequently used operations, such as factoring or expanding binomials. These techniques save valuable time.
Break Down Complex Problems: Divide larger problems into smaller, more manageable steps to avoid feeling overwhelmed and reduce errors.

Tools and Techniques for Faster Solving

Use of Graphing Calculators: For more complicated equations or to visualize relationships between variables, using a graphing calculator can provide instant solutions and insights.
Work in Reverse: Sometimes working backwards from the desired result can be quicker than following the standard solution process, especially when you know the end goal.
Use of Estimation: Estimating values instead of solving for precise answers can help speed up your approach, especially when the exact solution isn’t necessary for the given problem.
Group Similar Problems: Practice solving similar problems in groups to speed up recognition of patterns and improve efficiency.

How to Check Your Answers

Verifying your solutions is a crucial step in problem-solving. Ensuring that your calculations and logic are correct not only boosts confidence but also helps prevent errors from going unnoticed. There are several methods to check your work, ranging from simple verification steps to more advanced techniques, depending on the complexity of the problem.

One of the most effective ways to check your solutions is by substituting your final answer back into the original equation or problem. This allows you to see if the results hold true, ensuring that you haven’t made any miscalculations along the way. Additionally, reviewing the steps you took during the solution process can help identify any inconsistencies or assumptions that might have been incorrect.

In some cases, using alternative methods to approach the same problem can provide further validation. If the answer remains consistent across different techniques, you can be more confident that your solution is correct. Whether it’s checking with a different formula, method, or even using estimation, cross-verifying your results is a key part of ensuring accuracy.

Section 7 Practice Exercises

Practicing problems is an essential part of mastering any mathematical concept. In this part, you’ll find a series of exercises designed to reinforce the key skills and techniques discussed earlier. These problems range in difficulty and aim to help you apply the methods you’ve learned to various scenarios.

By working through these exercises, you’ll develop a deeper understanding of the material and improve your problem-solving speed. It’s important to approach each problem methodically, using the strategies and tips shared in the previous sections to guide you toward the correct solution.

Exercise Set 1

Solve for x: 3x + 5 = 20
Solve for y: 2y – 4 = 12
Find the value of z in the equation: 4z + 7 = 27

Exercise Set 2

Solve the quadratic equation: x² – 5x + 6 = 0
Factor the expression: x² + 3x – 10
Find the roots of the equation: x² + 2x – 8 = 0

Make sure to check your solutions and review the methods used for each problem. Regular practice will help solidify your understanding and build your confidence in solving more complex challenges.

Resources for Additional Help

If you’re looking for extra support to improve your understanding of the material, there are several excellent resources available to you. These tools can offer guidance, provide practice opportunities, and help clarify complex concepts that may be difficult to grasp on your own.

Many online platforms, video tutorials, and educational websites offer free and paid services, catering to learners of all levels. Whether you’re seeking detailed explanations, step-by-step solutions, or interactive exercises, you’ll find a variety of options to suit your needs.

Here are some helpful resources to consider:

Online Tutoring Platforms: Websites like Khan Academy and Wyzant offer personalized tutoring sessions and video lessons that cater to different learning styles.
Interactive Practice Websites: Tools like IXL and Brilliant provide interactive exercises that adapt to your skill level and allow for targeted practice.
YouTube Educational Channels: Channels such as PatrickJMT and Professor Leonard offer in-depth video tutorials that break down complex topics into easy-to-understand lessons.
Textbooks and Workbooks: Many textbooks and workbooks come with companion websites that offer additional problems, solutions, and explanations to reinforce key concepts.

By utilizing these resources, you can continue to enhance your learning experience and work towards mastering the material. Don’t hesitate to reach out for extra help whenever needed, as consistent practice and support are key to success.

Preparing for Tests and Quizzes

Preparing for upcoming tests and quizzes can be a challenging yet rewarding task. It’s important to approach the process strategically to ensure you’re ready to tackle any question with confidence. Effective preparation involves not just reviewing materials but understanding key concepts, practicing problems, and managing time efficiently.

Here are some essential strategies to help you prepare:

1. Organize Your Study Materials

Start by gathering all relevant study materials, including notes, textbooks, past assignments, and practice sheets. Organizing your materials will help you focus on the most important topics and avoid unnecessary distractions.

2. Focus on Key Areas

Identify the most frequently tested concepts and areas that you may find challenging. Spend extra time reviewing these topics and practicing related problems to ensure you’re fully prepared.

Key Topic	Suggested Practice
Equations	Solve different types of equations with varying difficulty
Word Problems	Break down problems step by step, focusing on identifying key information
Graphing	Practice plotting different types of graphs and interpreting them

Other Tips:

Take breaks to avoid burnout – short, frequent study sessions are more effective than long, exhausting ones.
Test yourself with practice questions to get a sense of the format and time constraints.
Review any mistakes you make on practice problems to identify areas where you need further improvement.

By staying organized, focusing on key topics, and practicing consistently, you’ll be well-equipped to perform your best during tests and quizzes. Don’t hesitate to ask for help if you encounter challenges, as clarification can boost your confidence and understanding.