
Understanding complex mathematical concepts can be challenging, especially when tackling a series of exercises designed to test your skills. The following section provides guidance and solutions to help clarify difficult problems and reinforce key principles. By reviewing the solutions, students can gain deeper insights into various methods of approaching and solving problems.
As you work through each section, it is important to not only check the results but also understand the process behind each solution. This approach ensures that learning extends beyond memorization and fosters a stronger grasp of the underlying mathematical ideas. Whether for self-assessment or homework completion, this resource serves as a valuable tool to improve your understanding and boost your confidence in the subject.
Core Connections Course 3 Answer Key
In this section, we provide solutions to various exercises, enabling learners to check their progress and gain a clearer understanding of key mathematical principles. By reviewing these solutions, students can identify the methods used to solve each problem, reinforcing their comprehension and improving their ability to apply these techniques to new challenges.
Benefits of Reviewing Solutions
Examining detailed solutions allows students to recognize patterns and strategies that they might have missed during their initial attempts. This process not only helps in verifying results but also enhances problem-solving skills by showcasing different approaches to similar challenges. Gaining familiarity with the methods presented can significantly improve both accuracy and confidence in future tasks.
How to Use This Resource Effectively
To make the most of this guide, focus on understanding the steps involved in each solution. Pay attention to the reasoning and logic behind the answers, rather than just memorizing the final result. This approach will deepen your mathematical reasoning and provide the tools needed to tackle even more complex problems down the line.
Understanding the Core Connections Curriculum
The program is designed to guide students through a progressive journey of mathematical learning, where foundational concepts are introduced and built upon over time. The approach emphasizes not only the mastery of core ideas but also the development of critical thinking and problem-solving skills. This structured path ensures that students are well-equipped to tackle increasingly complex topics as they advance.
Key Concepts and Areas of Focus
Throughout the program, students are exposed to a wide range of mathematical topics, each targeting essential skills and concepts that are crucial for their academic growth. The curriculum is structured in such a way that each new concept builds upon previous knowledge, allowing learners to deepen their understanding step by step.
| Mathematical Concept | Key Focus Areas |
|---|---|
| Number Operations | Understanding basic operations, fractions, decimals |
| Geometry | Shapes, angles, measurement techniques |
| Algebra | Solving equations, patterns, variables |
| Data and Probability | Graphing, analyzing data sets, probability principles |
Building Problem-Solving Skills
The program prioritizes developing problem-solving abilities by challenging students to apply mathematical principles in various contexts. Through a series of progressively challenging exercises, learners are encouraged to think critically, analyze different approaches, and find the most efficient solutions. This method fosters a deeper understanding of mathematics and prepares students for future academic endeavors.
How to Use the Answer Key Effectively

Utilizing a solution guide can be an invaluable tool when studying, but it is important to use it strategically. The goal should be to understand the methods and reasoning behind each solution, rather than simply copying answers. When approached with the right mindset, this resource can significantly enhance learning by clarifying concepts and showing different approaches to solving problems.
To make the most of this guide, start by attempting each exercise on your own first. Once you’ve tried a problem, compare your solution with the one provided. Focus on understanding why the solution works and what steps were taken to reach the conclusion. If there’s a difference between your approach and the solution, take the time to analyze where your reasoning diverged and learn from it.
Active engagement with the provided solutions helps to reinforce key concepts and improve your problem-solving strategies. Avoid using the guide as a shortcut; instead, treat it as a tool for learning, allowing it to guide your thought process and enhance your critical thinking skills.
Revisiting exercises after reviewing the solutions is also a great way to strengthen your understanding. The more you practice, the more confident you will become in tackling similar challenges in the future.
Key Concepts in Core Connections Course 3
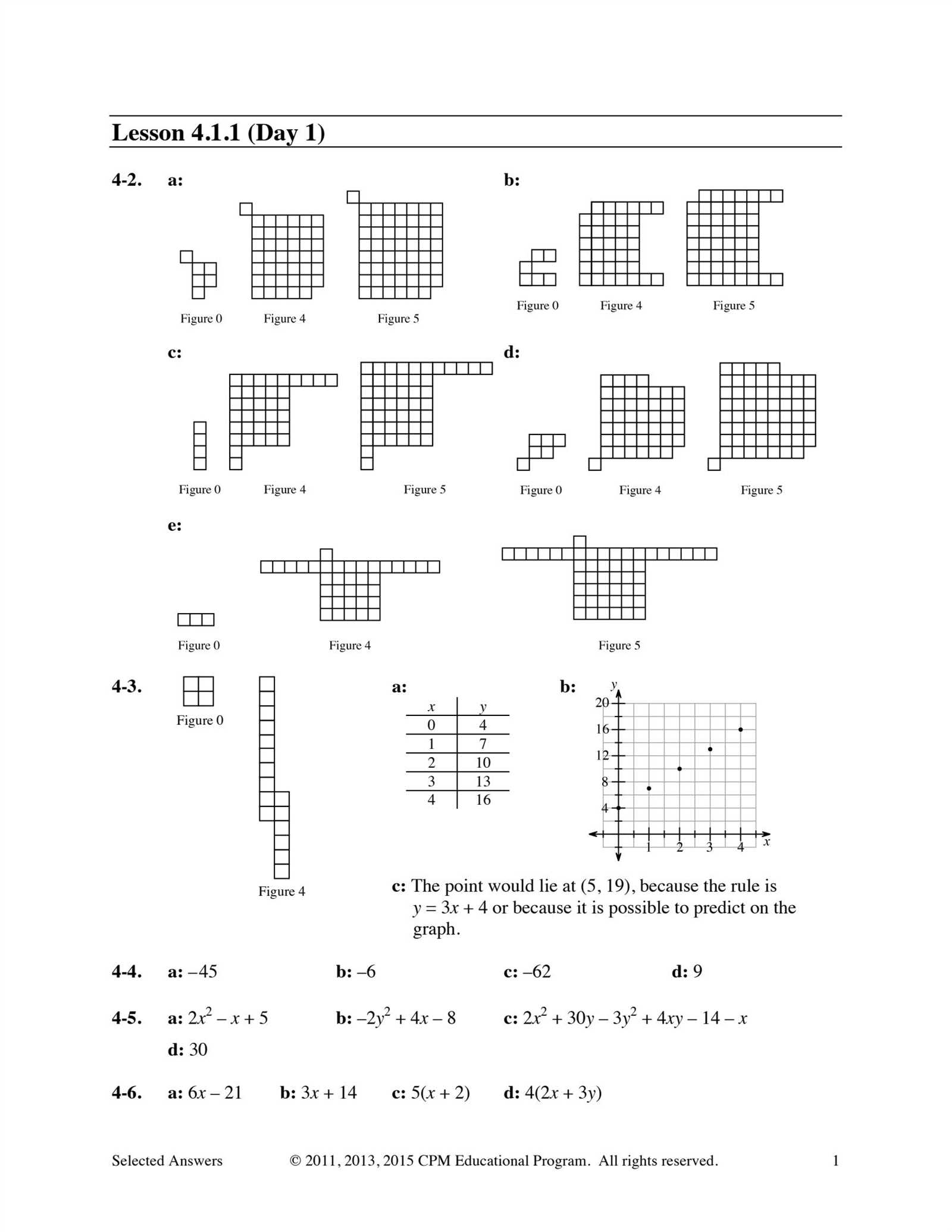
Throughout this program, students are introduced to a series of essential mathematical principles that serve as the foundation for advanced topics. These concepts are carefully designed to build a strong understanding of both basic and complex ideas, enabling learners to approach more difficult challenges with confidence. The focus is on reinforcing fundamental skills while also encouraging critical thinking and problem-solving abilities.
One of the main areas of focus is mastering mathematical operations, including fractions, decimals, and percentages. Students learn how to perform calculations with precision, a skill that is crucial for tackling a wide range of problems. In addition, geometry is explored, with emphasis on shapes, angles, and measurement techniques. By learning to visualize and calculate properties of different figures, students strengthen their spatial reasoning abilities.
Algebra is another core concept that is deeply explored, where students gain proficiency in working with variables, solving equations, and understanding mathematical relationships. The ability to manipulate algebraic expressions is key to solving more complex problems in mathematics. Furthermore, the study of data analysis and probability prepares learners to interpret and analyze real-world situations using mathematical models, which is essential for making informed decisions.
Benefits of Using the Answer Key
Having access to a solution guide can provide several advantages for students working through challenging mathematical problems. It serves as a tool for self-assessment, allowing learners to verify their results and identify areas for improvement. By reviewing the solutions, students can also gain deeper insights into the problem-solving process, helping them develop stronger analytical skills.
Enhanced Understanding of Problem-Solving Techniques
One of the primary benefits of using a solution guide is that it reveals the step-by-step methods used to solve each problem. This not only ensures that students arrive at the correct answers but also helps them understand the reasoning behind each step. This methodical approach to problem-solving is essential for mastering more complex topics.
- Reveals multiple ways to approach problems
- Helps identify common mistakes
- Improves efficiency in solving similar problems
Boosting Confidence and Motivation
When students can check their work and understand the correct methods, it helps boost their confidence in their abilities. This sense of achievement is motivating, encouraging them to tackle more difficult exercises with less hesitation. Regularly reviewing solutions can also reduce the frustration that often accompanies challenging tasks.
- Provides reassurance when answers match
- Reduces anxiety about complex problems
- Encourages continuous learning and practice
Important Topics Covered in the Course
This program covers a variety of critical mathematical concepts that are fundamental for developing a deep understanding of the subject. From foundational operations to more advanced applications, the material is designed to provide students with a well-rounded education in key areas that will be crucial for their academic progression. Each topic is explored in depth, allowing learners to grasp the material fully before moving on to more complex challenges.
Mastering Arithmetic and Number Operations
One of the essential areas covered is arithmetic, where students refine their skills in performing basic operations such as addition, subtraction, multiplication, and division. Emphasis is placed on understanding fractions, decimals, and percentages, which are integral to many real-world applications. Mastering these skills is critical as they form the foundation for more advanced mathematical concepts.
Exploring Algebra and Problem Solving
Algebra plays a significant role in this program, with students learning how to manipulate variables, solve equations, and understand mathematical relationships. By working through various problems and exercises, learners gain valuable problem-solving experience that strengthens their ability to approach complex situations with confidence. Algebra is not just about solving equations; it’s about developing logical thinking and analytical skills that will be useful across different areas of study.
Common Mistakes and How to Avoid Them
While working through mathematical exercises, it’s common for students to encounter certain mistakes that can hinder their progress. These errors often arise from misunderstandings of key concepts, miscalculations, or overlooked details. Recognizing and addressing these mistakes is essential for improving problem-solving skills and ensuring a more thorough understanding of the material.
Frequent Errors in Mathematical Operations
One of the most common mistakes involves incorrect calculations, particularly when dealing with fractions, decimals, or percentages. Students may also misinterpret word problems or skip steps in complex equations. To avoid these pitfalls, it’s crucial to take time with each calculation, double-checking each step before moving forward.
- Skipping steps in multi-step problems
- Incorrectly simplifying fractions or decimals
- Misreading or misunderstanding problem instructions
Strategies for Avoiding Mistakes
Developing careful habits and reviewing solutions can help students identify where they went wrong. Practicing regularly and reviewing both correct and incorrect approaches allows for a deeper understanding of problem-solving methods. Additionally, breaking down problems into smaller steps can reduce errors and improve accuracy.
- Slow down and double-check each step
- Understand the problem fully before solving it
- Review mistakes and learn from them
How the Solution Guide Supports Learning
Using a solution guide can greatly enhance the learning process by providing clear, step-by-step explanations of how to approach and solve various problems. Rather than merely offering answers, it helps students understand the methods and reasoning behind each solution. This not only reinforces their current knowledge but also encourages deeper engagement with the material, enabling learners to apply these techniques independently in the future.
Building Problem-Solving Skills
One of the key benefits of using a solution guide is its ability to demonstrate different problem-solving strategies. It shows how to break down complex tasks into smaller, more manageable steps, allowing students to approach challenges with confidence. By seeing the process unfold, learners can adopt and adapt these strategies to solve similar problems on their own.
Encouraging Active Learning

Rather than passively relying on the guide, students should actively engage with it. This means attempting the problems first, then using the solution guide to verify their approach and understand any mistakes. This process of comparison and reflection fosters critical thinking and deepens understanding, making the learning experience more effective.
Overview of Course 3 Problem Types
This section explores the various types of problems students will encounter in this level of study. The problems are designed to cover a broad range of mathematical concepts, helping learners develop a deep understanding of the subject matter. Each problem type challenges different skills, from basic arithmetic to more complex problem-solving and algebraic reasoning.
Throughout the program, students will encounter problems that require them to apply their knowledge in practical ways. These tasks often involve working with numbers, variables, and equations, as well as interpreting data and making connections between different mathematical concepts. By mastering these different types of problems, learners can build a strong foundation for future mathematical studies.
Tips for Solving Problems Effectively
When tackling mathematical problems, it is important to approach them systematically. Whether dealing with simple calculations or more complex equations, a strategic method can help improve accuracy and efficiency. By applying these tips, students can enhance their problem-solving skills and gain greater confidence in their abilities.
First, it’s essential to fully understand the problem before attempting to solve it. Carefully read through the instructions and identify what is being asked. Once you have a clear understanding, break the problem down into smaller, manageable parts. This will help ensure that no steps are missed and reduce the chances of making mistakes.
| Tip | Description |
|---|---|
| Read Carefully | Ensure you understand the problem and what is being asked before starting the solution. |
| Break It Down | Divide the problem into smaller steps to avoid feeling overwhelmed and to simplify the process. |
| Check Your Work | After solving, review each step to verify accuracy and ensure that the final solution is correct. |
| Practice Regularly | The more problems you solve, the more confident you will become in applying the methods and techniques. |
By following these strategies, students can approach any problem with a clear plan and reduce the likelihood of making errors. Regular practice, combined with careful attention to detail, is key to becoming proficient in mathematics.
How to Track Progress with the Solution Guide
Tracking your progress is an essential part of the learning process, helping you identify areas where you’ve improved and areas that still need attention. By using a solution guide strategically, students can monitor their development over time. This guide not only provides solutions but also helps to understand the process, allowing learners to measure their ability to apply techniques correctly.
As you work through problems, it’s important to check your work against the solutions provided, not just for correctness but for understanding. If you find discrepancies, take note of where you made errors, and focus on those areas for improvement. This reflective practice helps ensure continuous growth in both problem-solving skills and comprehension of the material.
Consider keeping a record of the problems you’ve completed, noting how confident you feel in your solutions. Over time, this record will help you see trends in your progress, highlighting areas where you may need additional practice or where you’ve mastered the material.
Using the Solution Guide for Self-Assessment
Self-assessment is a powerful tool for understanding your strengths and identifying areas that need improvement. By referring to a solution guide, you can evaluate your own understanding of the material and track your learning progress. This method encourages independent learning and allows you to take control of your educational journey.
When using the solution guide for self-assessment, it’s important to follow a structured approach. Here are a few steps to make the most of this process:
- Compare your solutions: After solving a problem, check your work against the guide. If your solution matches, it shows you’re on the right track.
- Analyze mistakes: If your solution differs, take time to review the steps you took and identify where the error occurred. This helps you understand the reasoning behind the correct answer.
- Track progress: Keep a log of problems you’ve worked through, noting which areas you feel confident in and which ones need more practice.
- Reflect on understanding: Ask yourself if you fully understand why the solution works. It’s important to grasp the concept, not just the outcome.
By regularly using the solution guide for self-assessment, you’ll build a deeper understanding of the material and continuously refine your problem-solving skills.
Examples of Key Problems from the Program
Understanding the types of problems encountered in a mathematical program can significantly enhance a student’s ability to approach challenges confidently. The following examples showcase important problems that illustrate various concepts and problem-solving methods. These examples provide a deeper understanding of the material and help students apply what they’ve learned in practical scenarios.
Example 1: Solving Linear Equations
One common problem involves solving linear equations. For instance, you might be tasked with solving for the unknown variable in an equation like 2x + 5 = 15. This problem requires the application of basic algebraic principles such as isolating the variable and simplifying the equation step by step.
Example 2: Working with Ratios and Proportions
Another key problem involves ratios and proportions. Students may encounter problems such as finding the missing value in a proportion, like 3/5 = x/15. These types of problems test the ability to recognize relationships between quantities and use cross-multiplication to find the unknown.
Strategies for Mastering Essential Concepts
Mastering fundamental concepts in any subject requires a combination of effective study techniques, consistent practice, and a deep understanding of the core principles. By adopting the right strategies, learners can strengthen their grasp of key topics and enhance their ability to solve complex problems. Below are several approaches that can help learners excel and retain important knowledge.
Active Practice and Application
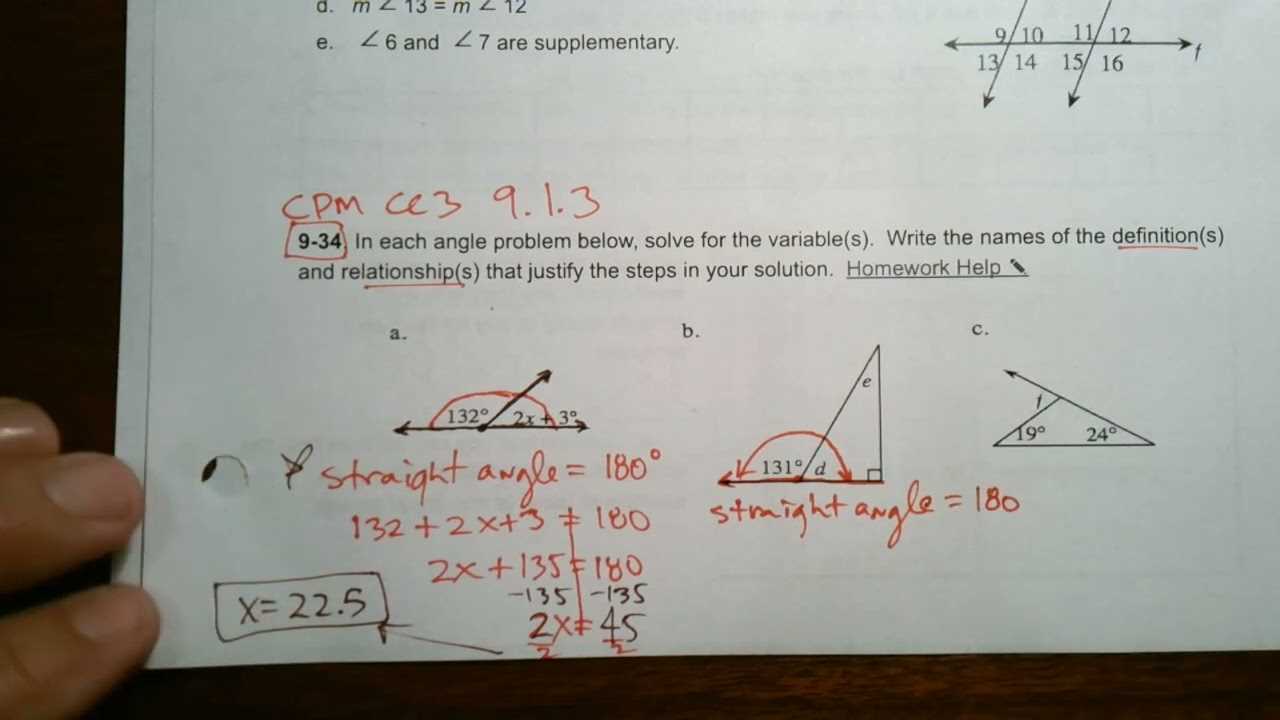
One of the most effective ways to solidify understanding is through active practice. This involves regularly solving problems related to the concepts being studied. Rather than just reviewing notes or reading through examples, actively engaging with the material will help reinforce learning and reveal areas that need more focus.
- Consistent problem-solving: Set aside dedicated time each day to solve problems. This repetition helps to build familiarity and confidence with the material.
- Applying concepts to real-life scenarios: Look for opportunities to apply what you’ve learned in practical situations. This reinforces the relevance of the concepts and improves retention.
Breaking Down Complex Problems
Complex problems can often seem overwhelming at first. However, breaking them down into smaller, manageable steps makes them easier to tackle. This approach not only simplifies the problem-solving process but also helps clarify the underlying concepts.
- Identify key components: Start by identifying the important elements in the problem. Break it down into smaller parts to tackle each one individually.
- Work through each step logically: Approach each part methodically, ensuring that you fully understand each step before moving on to the next.
How Teachers Can Utilize the Answer Guide
Teachers play a crucial role in guiding students through the learning process. Utilizing a detailed solution guide can significantly enhance teaching effectiveness by providing quick access to correct solutions and offering insights into common problem areas. By leveraging this tool, educators can better support their students’ development and address individual learning needs.
Guiding Instruction and Reinforcing Learning
One of the primary ways that educators can make use of the solution guide is by helping students understand the reasoning behind correct solutions. Instead of merely providing answers, teachers can walk students through the problem-solving process, encouraging critical thinking and a deeper comprehension of the concepts.
- Facilitating class discussions: After reviewing solutions, teachers can use the guide to prompt discussions, allowing students to explain their reasoning and compare methods with their peers.
- Identifying common mistakes: By analyzing the errors students make, teachers can provide targeted instruction to address misconceptions and reinforce understanding.
Personalizing Student Support
The solution guide can also help teachers personalize their approach to individual students. By identifying areas where certain students may be struggling, educators can provide additional resources or offer tailored explanations to improve understanding.
- Targeted interventions: Use the guide to identify patterns in students’ errors and offer additional practice or clarification in those specific areas.
- Encouraging self-assessment: Teachers can guide students in using the solution guide for self-reflection, helping them assess their progress and identify areas for improvement.
Where to Find Additional Resources for Practice
In order to fully master the material, students often need more than just the exercises found in textbooks or guides. There are numerous supplementary resources available to help reinforce learning, offering extra practice, varied problem types, and deeper insights into complex topics. Exploring these resources can aid in honing skills and ensuring a solid understanding of the subject matter.
Many online platforms, educational websites, and learning apps provide a wealth of exercises and interactive content that can complement traditional study methods. These platforms cater to a range of learning styles, allowing students to access resources in formats such as video tutorials, quizzes, and step-by-step problem-solving guides.
- Interactive Learning Websites: Websites like Khan Academy and Coursera offer free lessons, practice problems, and instructional videos that explain key concepts in-depth.
- Online Practice Platforms: Platforms such as IXL or Quizlet provide customized exercises, quizzes, and flashcards that can help students practice and reinforce specific skills.
- Math Forums and Communities: Websites like Stack Exchange or Reddit’s learning communities allow students to discuss problems with peers and experts, gaining new perspectives on difficult topics.
- Mobile Apps: Educational apps like Photomath or Wolfram Alpha can help students with step-by-step solutions and explanations on the go.
By utilizing a combination of these resources, students can ensure continuous improvement and strengthen their grasp on challenging concepts, all while fostering independent learning habits that will benefit them in the long run.