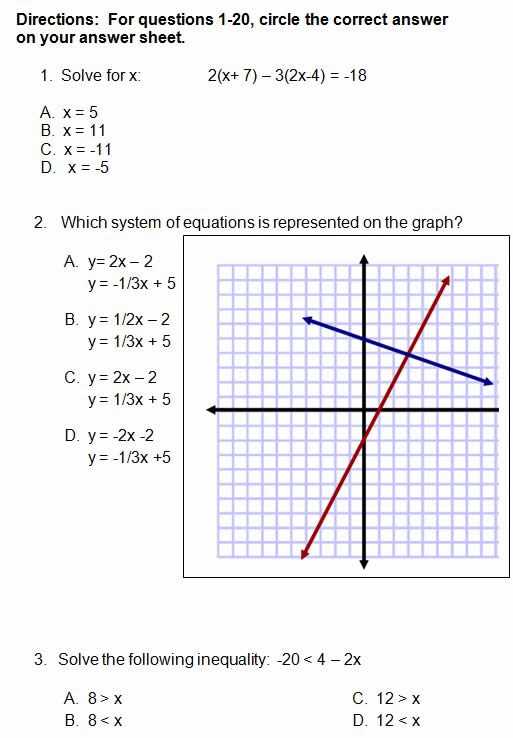
Success in mathematics often depends on understanding fundamental principles and practicing various problem-solving techniques. Developing a strong foundation in critical topics is key to building confidence and achieving excellent results in assessments.
This guide focuses on practical methods and strategies to help you navigate through challenging problems. Whether you’re revisiting essential concepts or exploring new approaches, the goal is to enhance your understanding and boost your performance in evaluations.
By emphasizing structured practice and clear explanations, you’ll gain the tools needed to tackle even the most complex calculations with ease. Dive in to discover effective techniques and helpful tips that will support your learning journey.
Understanding Key Concepts in Algebra
Mathematical problem-solving relies heavily on grasping foundational ideas that form the basis of more complex operations. Recognizing patterns, identifying relationships, and applying logical reasoning are essential skills for tackling various tasks effectively.
The Importance of Foundational Knowledge
Building a strong base in mathematics involves mastering fundamental operations, such as addition, subtraction, multiplication, and division, alongside more advanced techniques like simplifying expressions and recognizing number properties. These basics provide the groundwork for understanding how different elements interact within equations and systems.
Applying Logic to Problem Solving
Logical thinking allows for a step-by-step approach to finding solutions. Breaking down complex challenges into smaller, manageable parts makes it easier to identify errors and correct them. This structured method not only improves accuracy but also enhances overall comprehension.
Strategies for Solving Linear Equations
Solving relationships involving unknown values and constants requires a structured approach. Breaking the process into manageable steps helps ensure accuracy and simplifies even complex challenges.
Essential Techniques for Solving

- Combine similar terms: Organize like terms on the same side to simplify the expression.
- Isolate the unknown: Rearrange the equation so that the variable stands alone on one side.
- Clear fractions or decimals: Multiply through by a common factor to eliminate fractions or simplify decimal values.
- Simplify further: Divide or multiply as needed to solve for the unknown completely.
Common Errors and How to Avoid Them
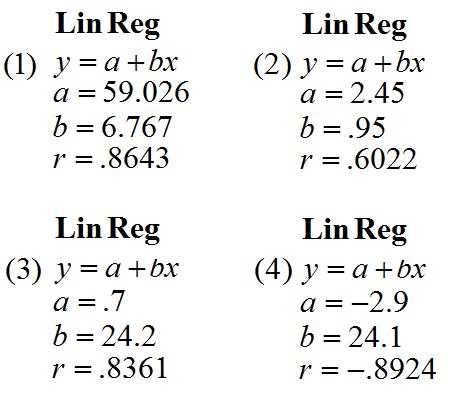
- Overlooking the order of operations: Always
Tips for Factoring Quadratic Expressions
Breaking down mathematical expressions into simpler components can make solving problems much more manageable. By recognizing patterns and applying specific techniques, you can transform complex forms into easily solvable pieces.
Key Methods for Simplification
Different approaches work for different expressions, but understanding when and how to apply each one is essential for efficiency. Below are common techniques and their uses:
Method When to Use Example Common Factor When all terms share a common divisor 6x² + 9x → 3x(2x + 3) Difference of Squares For expressions with two terms, one positive and one negative x² – 16 → (x + 4)(x – 4) Grouping When terms can be rearranged into two pairs x² + 5x + 6 → (x + 2)(x + 3) Common Mistakes to Avoid
- Skipping checks: Always verify by multiplying the factors back together.
- Overlooking negatives: Pay attention to signs, especially in multi-term expressions.
- Rushing the process: Carefully review each step to avoid minor errors.
By mastering these strategies and practicing regularly, you’ll gain confidence and accuracy in simplifying even the trickiest expressions.
How to Simplify Algebraic Fractions
Simplifying mathematical expressions involving ratios of polynomials can make problem-solving faster and more efficient. By carefully reducing both the numerator and denominator, you can make complex expressions easier to handle.
Steps for Simplification

Start by factoring both the numerator and denominator, then cancel out any common factors. This process helps reduce the fraction to its simplest form.
- Factor both parts: Look for common factors in both the numerator and denominator.
- Cancel out common factors: Once the terms are factored, eliminate any repeating factors from both the top and bottom.
- Reduce the expression: If possible, divide through by the greatest common divisor to further simplify.
Common Pitfalls to Avoid
- Skipping factoring: Don’t try to cancel terms before factoring; it may lead to incorrect results.
- Incorrectly canceling terms: Be sure that the factors are common in both parts before removing them.
- Ignoring restrictions: Always check for values that make the denominator equal to zero, as this is undefined.
By following these steps and practicing regularly, you’ll become proficient in simplifying even the most complicated fractions.
Graphing Linear Functions Made Simple
Plotting straight-line relationships on a graph is an essential skill that can help visualize how variables interact with each other. The process involves identifying key elements of the function and then using these to create an accurate representation on a coordinate plane.
Step Action Example Identify Slope and Y-Intercept Find the values of slope (m) and the y-intercept (b) in the equation. y = 2x + 3 (slope = 2, y-intercept = 3) Plot the Y-Intercept Start by plotting the point where the line crosses the y-axis. Plot (0, 3) on the graph Use the Slope From the y-intercept, use the slope to find another point on the line. Rise 2 units and run 1 unit to plot another point Draw the Line Connect the points with a straight line. The line should pass through the points (0, 3) and (1, 5) Once you have your points, drawing the line will give you a clear visual of the relationship between the variables. This method is simple yet effective in understanding how two quantities are connected.
Steps to Solve Inequalities Effectively

Solving inequalities involves determining the range of values that satisfy a given condition. By following systematic steps, you can ensure that the process is both accurate and efficient, ultimately leading to a correct solution.
The key steps to solving inequalities include isolating the variable, applying operations to both sides while maintaining the inequality’s balance, and graphing the solution when needed. Additionally, understanding when to reverse the inequality sign is crucial for getting the right results.
First, you start by simplifying the inequality, which often involves moving terms to one side. Then, solve for the variable by performing inverse operations. Pay attention to any changes in direction when multiplying or dividing by negative numbers. Once you’ve found the solution, graphing the solution set on a number line can help visualize the result clearly.
Mastering Word Problems in Math
Word problems in mathematics can seem challenging at first, but with the right approach, they become more manageable. The key to solving these problems lies in translating the narrative into mathematical expressions and equations that you can work with. Understanding the context and identifying the main elements are the first steps toward finding a solution.
Steps to Solve Word Problems
Follow these steps to effectively solve word problems:
- Read Carefully: Ensure you fully understand the problem and all its details before proceeding.
- Identify Variables: Define what each unknown represents in the context of the problem.
- Set Up an Equation: Translate the words into a mathematical equation or inequality.
- Solve: Perform the necessary operations to find the solution.
- Check Your Work: Verify that the solution makes sense in the context of the problem.
Tips for Success
- Practice reading word problems slowly and carefully to ensure you catch all important details.
- Draw diagrams or create tables if the problem involves physical objects or quantities.
- Always double-check your final answer by plugging it back into the original equation to ensure it fits the context of the problem.
By consistently applying these strategies, you’ll find that tackling word problems becomes easier over time. Developing a systematic approach helps build confidence and improves problem-solving skills, making math more approachable and enjoyable.
Techniques for Solving System of Equations
When dealing with multiple unknowns in mathematical problems, solving a system of equations is essential. These problems often involve finding values for variables that satisfy all equations simultaneously. There are several methods that can be applied to efficiently solve these systems, each offering a unique approach depending on the structure of the equations.
The primary methods for solving these systems include substitution, elimination, and graphing. Each technique provides a distinct strategy for isolating and solving for the unknown variables.
Substitution Method

The substitution method is particularly useful when one equation is easy to manipulate in order to isolate one variable. Here’s how it works:
- Choose one of the equations and solve it for one variable.
- Substitute this expression into the other equation.
- Solve the resulting equation for the remaining variable.
- Substitute the value back into the original equation to find the value of the first variable.
Elimination Method
The elimination method is effective when both equations are aligned in such a way that you can eliminate one variable by adding or subtracting the equations. Follow these steps:
- Multiply or divide the equations if necessary to make the coefficients of one variable the same.
- Add or subtract the equations to eliminate one of the variables.
- Solve the resulting equation for the remaining variable.
- Substitute the value back into one of the original equations to solve for the other variable.
Both of these techniques, when applied correctly, will lead to the solution of the system, helping you find the values of the unknowns. The choice of method often depends on the specific structure of the equations involved and personal preference. With practice, these methods become quicker and more intuitive, allowing for faster solutions to complex problems.
Exploring Properties of Exponents
Understanding the properties of exponents is crucial in simplifying expressions and solving various mathematical problems. Exponents represent repeated multiplication, and knowing how to manipulate them effectively can make complex calculations more manageable. These properties serve as foundational tools that help simplify equations and aid in the understanding of more advanced concepts.
Several key properties of exponents are used regularly to simplify expressions. These include the product rule, quotient rule, power rule, and negative exponent rule. Each of these properties offers a way to break down complicated terms into simpler forms, making it easier to work with them in equations.
The product rule, for example, helps when multiplying terms with the same base, while the quotient rule comes into play when dividing such terms. The power rule simplifies expressions involving exponents raised to other exponents, and the negative exponent rule reveals how to express terms with negative exponents as fractions.
Mastering these properties can significantly improve your ability to solve problems and simplify expressions efficiently. They allow for quicker problem-solving and offer deeper insight into the behavior of numbers in various mathematical contexts.
Understanding Absolute Value Equations
Absolute value equations involve expressions where the unknown is enclosed within absolute value bars, which represent the distance of a number from zero on the number line. These types of equations have unique characteristics, as the solution is determined by the distance, regardless of direction. Understanding how to solve these equations requires a solid grasp of the basic principles of absolute values and the way they affect equations.
Solving Absolute Value Equations

To solve absolute value equations, the general approach is to set up two possible equations, because the absolute value of a number can be either positive or negative. This means that for an equation like |x| = a, the solutions could be x = a or x = -a. It’s important to consider both possibilities to ensure all potential solutions are found.
Equation Solution |x| = 5 x = 5 or x = -5 |x – 3| = 7 x – 3 = 7 or x – 3 = -7 Checking for Extraneous Solutions
It is essential to check for extraneous solutions after solving absolute value equations. Sometimes, when solving, the resulting solutions may not satisfy the original equation. Therefore, substitute the potential solutions back into the original equation to verify their validity.
Effective Study Methods for Tests
Preparation for assessments requires a strategic approach to maximize retention and performance. Developing a study plan that works with your personal strengths can make a significant difference. Understanding your own learning style and employing techniques that best suit it can help you retain information more effectively and approach the material with confidence.
Key Techniques for Effective Preparation
Using various study methods can help break down complex topics into manageable segments. Below are some effective strategies:
- Active recall: Regularly test yourself on the material instead of passively rereading notes.
- Spaced repetition: Review material at increasing intervals to reinforce long-term retention.
- Practice problems: Solve sample problems or exercises related to the topic to apply knowledge in context.
- Study groups: Discuss difficult concepts with peers to gain new insights and reinforce learning.
Creating a Study Schedule
Having a well-structured schedule can help break down your preparation into smaller, more achievable goals. Follow these steps to create a study plan:
- Determine the time available before the assessment.
- Break down the material into topics or units.
- Allocate time for each topic based on difficulty and importance.
- Include regular breaks to maintain focus and avoid burnout.
- Review your progress periodically and adjust your plan if necessary.
Common Mistakes to Avoid in Algebra
When solving mathematical problems, there are several pitfalls that can hinder progress and lead to incorrect results. Recognizing and addressing these common errors can improve accuracy and efficiency. By understanding where mistakes are most likely to occur, you can develop a strategy to avoid them and enhance your problem-solving skills.
1. Misunderstanding the Order of Operations
One of the most frequent errors occurs when the order of operations is not followed correctly. This can lead to incorrect calculations and answers. Always remember the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) to guide the sequence in which operations should be performed.
2. Incorrectly Applying Distribution
Distributive property errors are common when multiplying terms. It’s important to ensure that every term inside parentheses is multiplied by the term outside. For example, in the expression 3(x + 4), you must distribute the 3 to both x and 4, resulting in 3x + 12.
3. Forgetting to Simplify Expressions
Sometimes, after solving a problem, students forget to simplify their answers. This oversight can lead to unnecessarily complex results. Always double-check your final expression to ensure it is in its simplest form.
4. Mixing Up Positive and Negative Signs
Sign errors are another frequent mistake. Be especially cautious when adding or subtracting negative numbers. Always keep track of the signs, as they significantly affect the outcome of your calculations.
5. Failing to Check Solutions
After finding a solution, it’s crucial to substitute it back into the original equation to verify its correctness. This step helps catch any earlier mistakes and ensures the solution is valid.
Resources for Practice and Improvement
Improving problem-solving skills requires consistent practice and the right resources. With the right materials, learners can enhance their understanding and performance in various areas of mathematics. Here are some valuable tools and platforms to help reinforce concepts and build proficiency.
Online Learning Platforms
There are several online platforms offering interactive lessons, videos, and exercises to help deepen your understanding of mathematical concepts:
- Khan Academy: Offers a wide range of video tutorials and exercises for all levels of mathematics.
- Wolfram Alpha: A powerful tool for solving problems and understanding step-by-step solutions.
- Coursera: Provides courses from universities and educational institutions on various math topics.
Practice Workbooks and Guides
Books designed for self-study provide practice problems along with detailed solutions:
- Problem-Solving Workbooks: Look for books that focus on practice problems with varying difficulty levels to help challenge your skills.
- Solution Manuals: These often accompany textbooks and explain how to solve complex problems step-by-step.
- Study Guides: These offer concise explanations of key concepts, along with exercises to help reinforce learning.
Interactive Apps and Tools
Apps can provide immediate feedback, which is essential for learning. Some options include:
- Photomath: Helps solve problems by taking pictures of them and offering step-by-step solutions.
- Mathway: Provides instant answers and detailed breakdowns for various types of math problems.
- Brilliant: Offers interactive puzzles and challenges to deepen mathematical reasoning.
How to Interpret Function Notation
Understanding how to read and interpret function notation is essential for solving various mathematical problems. The notation provides a compact way to express relationships between variables, making it easier to work with functions. Below are key points to help in interpreting this symbolic language.
What is Function Notation?
Function notation is used to represent functions in a concise format. For example, ( f(x) ) denotes a function named “f” where ( x ) is the input, and the expression ( f(x) ) gives the output corresponding to that input.
Key Elements of Function Notation
- f(x): This represents the value of the function for a specific input ( x ). It can be interpreted as the output or result when ( x ) is substituted into the function.
- f(a): This indicates the output of the function when ( a ) is plugged into it, meaning ( f(a) ) is the value of the function when the variable is replaced by ( a ).
- f(x) = expression: In this format, the right side of the equation is an expression that defines how to compute the function’s output for any given input.
Interpreting Function Expressions

To interpret the function properly, follow these steps:
- Identify the function name and its input variable (e.g., ( f(x) ) where ( x ) is the input).
- Understand the operation defined by the function. For example, if ( f(x) = 2x + 3 ), then for any given ( x ), the output is obtained by multiplying ( x ) by 2 and then adding 3.
- Substitute the given input value into the function and calculate the output. For example, if ( f(x) = 2x + 3 ) and ( x = 4 ), then ( f(4) = 2(4) + 3 = 8 + 3 = 11 ).
By mastering function notation, you can easily understand and solve problems involving functions. It’s a powerful tool for representing mathematical relationships efficiently and accurately.
Solving Problems with Rational Expressions
Solving problems that involve rational expressions requires understanding how to manipulate fractions that have polynomials in the numerator and denominator. These expressions can be simplified, added, subtracted, multiplied, and divided, depending on the problem. Mastering these operations is essential for efficiently solving such problems.
Simplifying Rational Expressions
To simplify rational expressions, first factor the numerator and the denominator. If there are common factors, cancel them out. For example, if you have the expression ( frac{6x}{9x} ), you can simplify it by canceling the common factor of ( 3x ), which results in ( frac{2}{3} ).
Operations with Rational Expressions
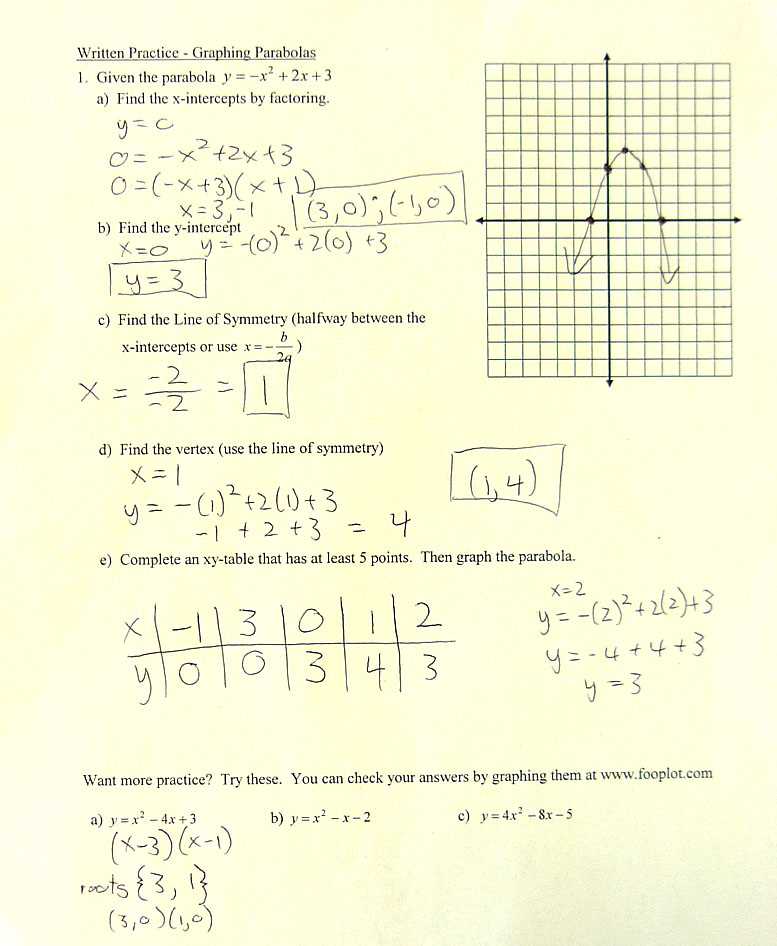
- Addition and Subtraction: To add or subtract rational expressions, first find a common denominator. Once you have a common denominator, combine the numerators and simplify the result.
- Multiplication: When multiplying rational expressions, multiply the numerators together and the denominators together. Simplify the resulting expression by canceling out common factors.
- Division: Dividing rational expressions is the same as multiplying by the reciprocal of the second expression. Flip the second fraction and multiply as you would in multiplication.
By following these steps and practicing regularly, you can develop a solid understanding of how to work with rational expressions, enabling you to tackle more complex problems with ease.
Benefits of Reviewing Past Exam Papers
Going over previous tests can be an extremely valuable practice when preparing for future assessments. It offers an opportunity to identify common question types, understand the structure of problems, and pinpoint areas that need improvement. By familiarizing yourself with the format and challenges, you can approach upcoming tasks with greater confidence and efficiency.
Understanding Question Patterns
One of the main advantages of reviewing past papers is recognizing recurring patterns. Many tests feature similar types of questions, so by practicing with old materials, you can develop a strategy to handle them more quickly and accurately. Whether it’s word problems, equations, or graphing, seeing familiar structures helps you become more comfortable with the task at hand.
Improving Time Management
- Timed Practice: Practicing with old papers under time constraints helps improve your pacing. This allows you to allocate time more effectively during the actual assessment.
- Identifying Difficult Areas: Past papers reveal which topics might require more attention. Understanding where you struggle enables focused study, ultimately enhancing your overall performance.
By actively engaging with past tests, you gain not only the ability to solve problems efficiently but also the confidence to tackle new challenges. Regularly reviewing old materials is a powerful tool for improving both knowledge and test-taking skills.