Achieving success in mathematics requires a solid understanding of fundamental principles and effective problem-solving strategies. Preparing for an important test in this subject can be overwhelming, but with the right approach, you can navigate through complex problems with confidence. This section will guide you through essential topics that are commonly tested, providing a clear path to mastering the material.
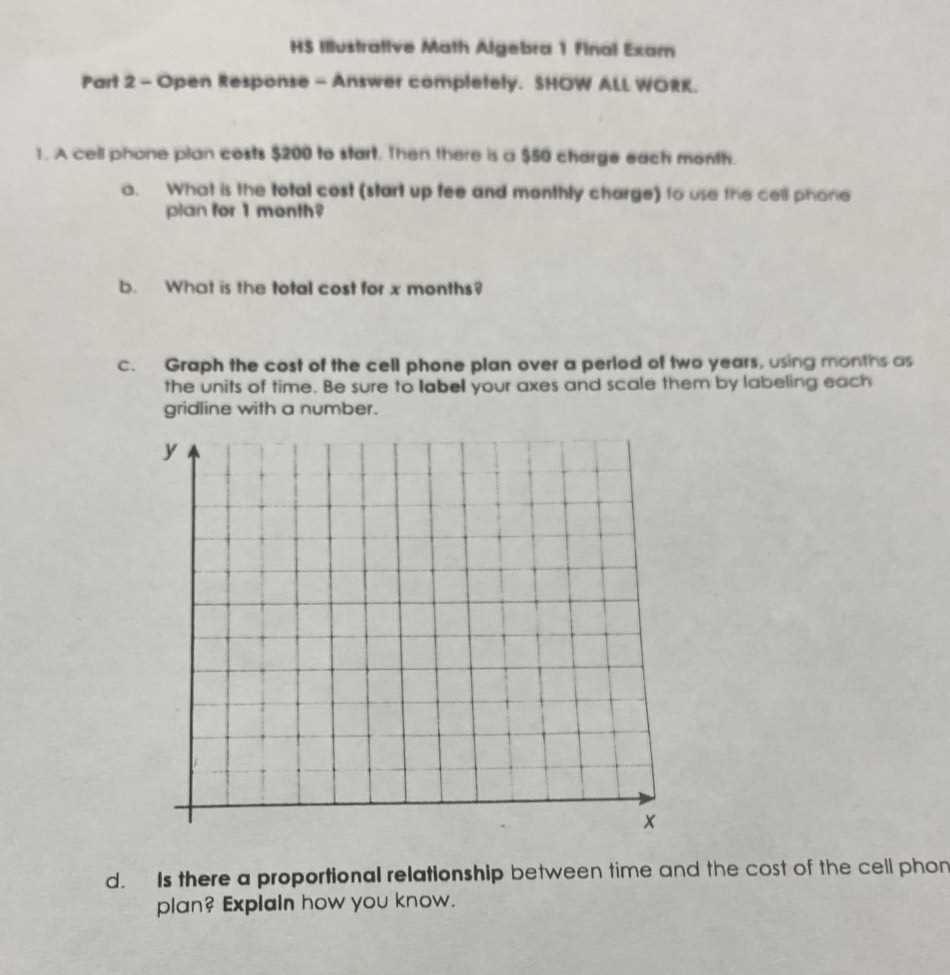
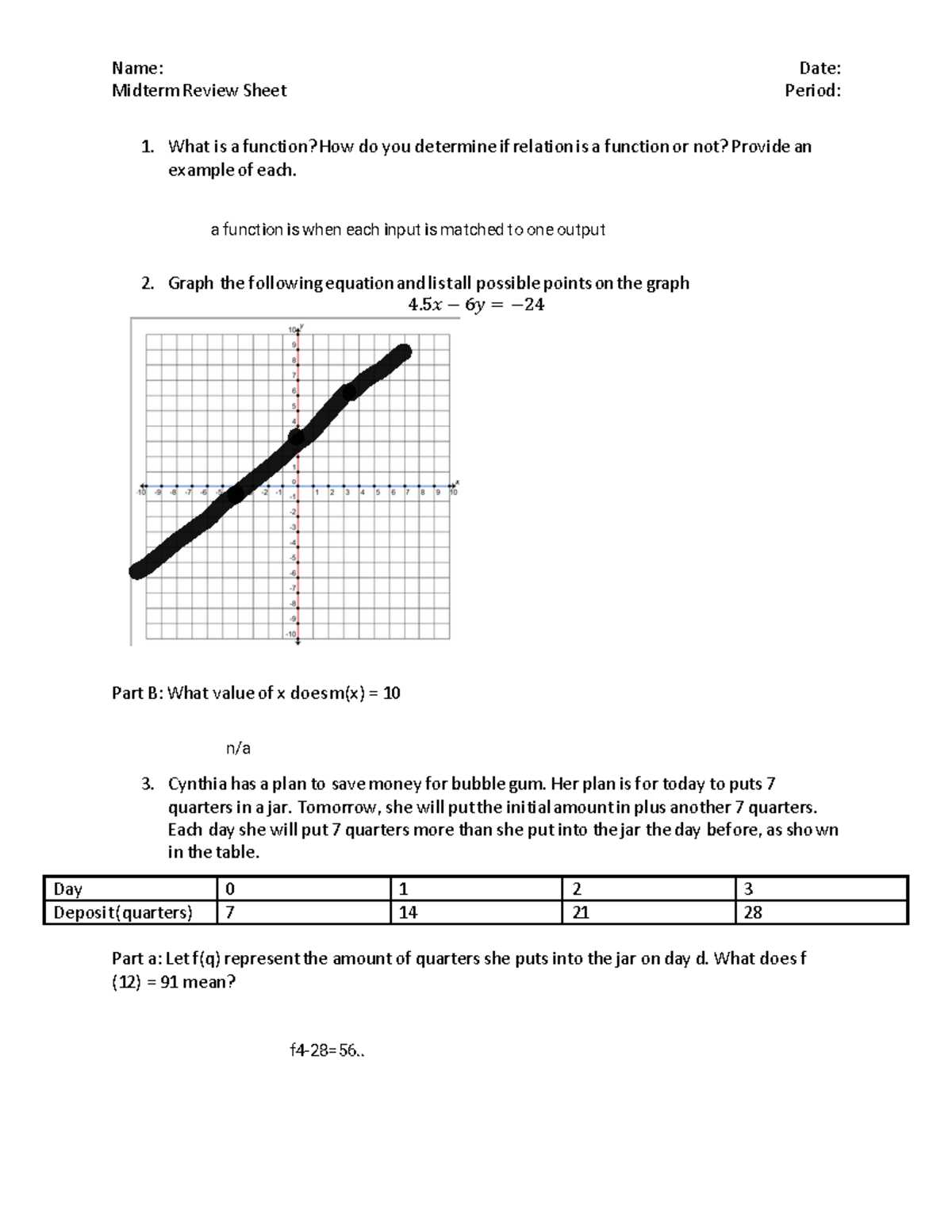
Understanding key formulas, techniques, and methods is crucial for tackling various types of questions. Whether it’s solving equations, working with functions, or interpreting graphs, each area requires a different set of skills. By reviewing examples and practicing problem-solving, you will become familiar with the most commonly asked questions and develop a structured approach to answering them.
Additionally, effective time management and study techniques play an important role in your preparation. Knowing when and how to allocate your time during both practice sessions and the actual assessment is essential for staying focused and organized. Mastering the material while improving your speed and accuracy will greatly contribute to your success.
Algebra 1 Midterm Exam Answers
Preparing for an assessment in mathematics can be a daunting task, but it becomes more manageable when you break down the material into clear steps. Understanding the structure of the questions and developing the ability to solve them systematically is key. This section will guide you through essential techniques and approaches that will help you approach each question with confidence and precision.
Common Question Types and Problem-Solving Strategies
Mathematical assessments often focus on specific topics such as equations, inequalities, and graph interpretation. Each problem type requires a unique approach, and learning how to identify the correct method will improve both accuracy and speed. Whether dealing with linear equations or more complex functions, the core principle is always the same: isolate the variable and solve step by step.
Mastering Key Formulas and Functions
One of the most important aspects of preparing for a math assessment is ensuring you have all relevant formulas and methods at your disposal. Key formulas related to solving equations, working with inequalities, and manipulating expressions are essential. Memorizing these can save time and reduce errors during the test. Additionally, practicing with functions and their applications will reinforce your understanding and help you recognize patterns.
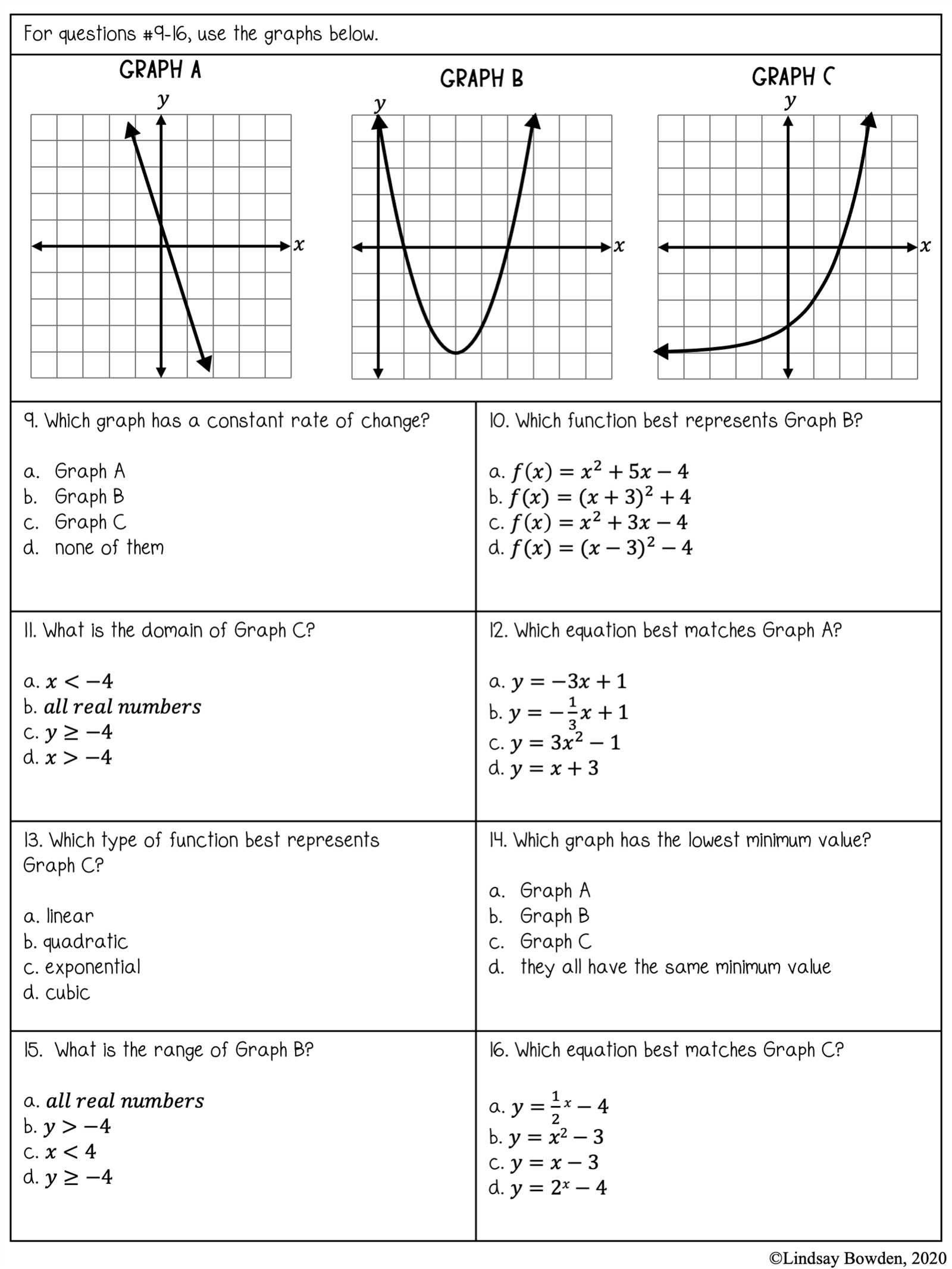
Effective practice is the best way to prepare. Regularly working through practice problems, reviewing solutions, and analyzing mistakes will sharpen your skills. Simulated practice sessions can also give you a feel for how to manage time during the actual test.
Mastering Key Algebra Concepts

To excel in mathematical assessments, it is crucial to have a strong grasp of the foundational concepts that are commonly tested. These core ideas form the building blocks for more complex problem-solving and can help you navigate through even the most challenging questions. By mastering these concepts, you will gain the confidence to tackle various problems efficiently.
Key Mathematical Concepts to Master
Understanding and applying essential mathematical principles is the first step toward success. The following topics are fundamental for problem-solving:
- Equations and Inequalities: Understanding how to manipulate and solve different types of equations and inequalities.
- Functions and Graphs: Recognizing functions and how to interpret and plot their graphs.
- Exponents and Radicals: Working with powers, roots, and their properties.
- Factoring: Breaking down expressions into simpler components for easier solving.
- Systems of Equations: Solving for multiple variables using substitution and elimination methods.
Tips for Mastery and Retention
To truly master these concepts, regular practice and effective study habits are essential. The following strategies will enhance your understanding:
- Practice Consistently: Working through a variety of problems will reinforce your skills and help you recognize patterns.
- Understand the Process: Focus on the steps involved in solving each problem, not just the solution itself.
- Use Visual Aids: Diagrams and graphs can help you visualize concepts and make abstract ideas more tangible.
- Review Mistakes: Analyzing errors and understanding why they occurred can deepen your comprehension.
By dedicating time to mastering these core ideas, you will set yourself up for success and be well-prepared for any challenges that come your way during assessments.
Common Math Test Mistakes
During assessments, even the most prepared students can make simple errors that impact their performance. Recognizing these common mistakes and understanding how to avoid them can improve accuracy and increase confidence. By identifying where errors tend to occur, you can adjust your approach and minimize avoidable pitfalls.
Frequent Errors in Problem Solving
Many mistakes happen when students rush through problems or misinterpret key information. Below are some common issues to watch out for:
- Sign Errors: Neglecting to correctly apply positive and negative signs when solving equations or simplifying expressions.
- Incorrect Operations: Mixing up operations, such as adding instead of multiplying, especially when working with multiple terms or fractions.
- Misreading Word Problems: Skipping over critical information or misinterpreting the question’s requirements.
- Forgetting to Simplify: Failing to simplify expressions fully before reaching the final answer.
- Rounding Too Early: Rounding numbers too soon in calculations, leading to less accurate results.
How to Prevent These Mistakes
While mistakes are part of the learning process, being aware of common pitfalls and using strategies to avoid them can significantly improve your performance:
- Double-Check Your Work: Take the time to review each step before moving on to the next.
- Use Parentheses Carefully: Parentheses help you avoid confusion with the order of operations–always use them where necessary.
- Break Down Complex Problems: Break down larger problems into smaller, manageable steps to prevent mistakes from snowballing.
- Practice Word Problems: Get familiar with the phrasing of word problems so you can quickly identify what is being asked.
By paying attention to these common mistakes and incorporating preventive strategies into your study routine, you can reduce errors and boost your performance on any test.
How to Solve Algebraic Equations
Solving equations is a fundamental skill in mathematics that allows you to find the value of unknown variables. By following a step-by-step approach, you can systematically isolate the variable and solve for its value. Whether dealing with simple linear equations or more complex expressions, the key to success is understanding the operations and applying them correctly.
First, it’s important to identify the type of equation you are working with. In many cases, equations consist of an expression on both sides, with an equal sign separating them. The goal is to manipulate the equation until the variable is isolated on one side, making it easy to find its value. This can be done by performing the same operation on both sides of the equation, ensuring that the equality is maintained.
Once you’ve identified the operations, such as addition, subtraction, multiplication, or division, apply them systematically. For example, if you have an equation with a variable added to a constant, you can subtract the constant from both sides. Then, if the variable is multiplied by a number, you can divide both sides of the equation by that number.
Finally, always double-check your work. After solving for the variable, substitute your solution back into the original equation to ensure that both sides are equal. This final step will confirm that your solution is correct.
Tips for Math Test Preparation
Effective preparation is the key to performing well on any test. A well-structured study plan that incorporates practice, review, and time management will ensure that you are ready to tackle even the most challenging questions. By focusing on key topics, practicing problem-solving techniques, and developing a test-taking strategy, you can approach the assessment with confidence.
Start by reviewing the core concepts that are most likely to appear on the test. Focus on understanding the underlying principles behind each topic, rather than just memorizing steps. This deeper understanding will help you apply what you’ve learned to different types of problems. Make use of textbooks, online resources, and practice problems to reinforce your knowledge.
Incorporate regular practice sessions into your study routine. The more problems you solve, the more comfortable you will become with different question formats and techniques. Practice under timed conditions to simulate the test environment and develop good time-management skills. This will help reduce stress during the actual test and ensure that you can work efficiently.
Lastly, don’t forget to review your mistakes. When you get a problem wrong, take the time to understand why it happened and learn from it. This reflective process helps reinforce concepts and avoid making the same errors in the future. A balanced approach, combining practice, review, and reflection, will maximize your preparation and lead to better performance.
Understanding Math Word Problems

Word problems can be some of the most challenging questions in a math assessment, but they are also a great way to apply mathematical concepts in real-life scenarios. The key to solving these problems lies in translating the written information into mathematical expressions or equations. By breaking down the problem step by step, you can better understand what is being asked and how to approach the solution.
When faced with a word problem, the first step is to carefully read the problem and identify the important information. Look for key numbers, relationships between variables, and any conditions or constraints that are mentioned. Once you have a clear understanding of what the problem is asking, you can create an equation or expression that represents the situation described.
Below is a table that outlines a simple approach for solving word problems:
| Step | Action |
|---|---|
| 1 | Read the problem carefully and highlight key information. |
| 2 | Define the variables that represent the unknown quantities. |
| 3 | Translate the written relationships into a mathematical expression. |
| 4 | Solve the equation and find the value of the unknown variable. |
| 5 | Check your solution to ensure it makes sense in the context of the problem. |
By following these steps, you can break down complex word problems into manageable parts and solve them systematically. With enough practice, interpreting and solving these types of problems will become a more intuitive and less stressful process.
Common Mathematical Formulas You Need
In any math-related test or problem-solving scenario, knowing the key formulas is crucial for efficiency and accuracy. These fundamental equations allow you to solve a wide range of problems by providing a framework for calculating unknowns. Having a good grasp of these essential formulas can help you tackle both simple and complex problems with ease.
Basic Formulas for Key Concepts

Here are some of the most important formulas that you should be familiar with:
- Perimeter of a Rectangle: Perimeter = 2(length + width)
- Area of a Triangle: Area = 1/2 × base × height
- Slope of a Line: m = (y₂ – y₁) / (x₂ – x₁) (used for calculating the slope between two points)
- Pythagorean Theorem: a² + b² = c² (for right-angled triangles)
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a (for solving quadratic equations)
Why These Formulas Matter
Mastering these formulas is essential because they simplify the problem-solving process. By using these formulas, you can reduce complex problems into straightforward calculations. These essential equations are foundational, not just for basic problem-solving, but also for progressing to more advanced topics in mathematics.
With continuous practice and application of these formulas, you will gain confidence and improve your ability to solve a variety of problems quickly and accurately.
Effective Study Strategies for Mathematics
Studying for a math assessment requires more than just reviewing notes; it involves developing a structured approach to master key concepts and solve problems with confidence. The right study techniques can help you retain information, identify weaknesses, and build problem-solving skills. By implementing focused strategies, you can improve your understanding and performance in mathematics.
Key Study Approaches
Here are some effective strategies for preparing for math assessments:
| Strategy | Description |
|---|---|
| Active Practice | Work through problems regularly to reinforce concepts and techniques. The more you practice, the more familiar the problems will become. |
| Break Down Complex Problems | Divide complicated questions into smaller, manageable steps. This will make it easier to understand and solve each part of the problem. |
| Use Study Aids | Leverage online resources, textbooks, and study groups to explore different explanations and approaches for solving problems. |
| Review Mistakes | Identify areas where you struggle and spend extra time practicing those topics. Analyzing your mistakes helps reinforce learning and prevent repetition. |
Building Confidence
Consistency is key when studying mathematics. By setting aside time each day to work through problems and review concepts, you’ll build both your knowledge and confidence. Avoid cramming before an assessment and focus on steady, incremental progress. Remember, the more time and effort you invest in mastering the material, the more confident and prepared you’ll feel come test day.
Reviewing Mathematical Expressions and Functions
Understanding mathematical expressions and functions is crucial for solving a variety of problems. These components are the building blocks of more complex equations, and reviewing them thoroughly ensures you can handle a wide range of problems with confidence. By focusing on their structure and behavior, you can better understand how to manipulate and solve them effectively.
Key Concepts in Expressions and Functions
When reviewing expressions and functions, it’s important to focus on key characteristics and operations that govern them. Here are some essential concepts:
| Concept | Description |
|---|---|
| Terms | Parts of an expression that are added or subtracted. They may include variables, constants, and coefficients. |
| Coefficients | The numerical factors that multiply the variables in an expression. |
| Constants | Fixed values that do not change within an expression, such as numbers like 5, 10, or -3. |
| Functions | Relations where each input corresponds to exactly one output. The function is often written as f(x) to represent the relationship between x and the output. |
Understanding Function Behavior
To fully grasp how expressions and functions work, it’s essential to understand their behavior. For example, analyzing how changes in variables affect the outcome of a function helps develop problem-solving strategies. Familiarity with how to solve for unknowns or simplify expressions will also significantly improve your ability to tackle more complex problems.
With regular practice, you can enhance your skills in manipulating and solving expressions, laying the foundation for tackling more advanced topics in mathematics.
Step-by-Step Guide to Solving Equations
Solving mathematical equations can seem complex at first, but by following a systematic approach, the process becomes much easier to understand and execute. Breaking down each problem into manageable steps allows you to isolate the unknown variable and find the solution efficiently. In this guide, we will walk through the essential steps involved in solving equations of various types.
Step 1: Simplify the Equation
Before attempting to solve the equation, simplify both sides as much as possible. This may involve distributing terms, combining like terms, or eliminating parentheses. The goal is to reduce the equation to its simplest form, which makes it easier to solve.
Step 2: Isolate the Variable
Once the equation is simplified, the next step is to isolate the unknown variable on one side of the equation. This typically involves moving constants and coefficients to the opposite side using addition, subtraction, multiplication, or division. Keep the equation balanced by performing the same operation on both sides.
Step 3: Solve for the Variable
With the variable isolated, you can now perform the final step to solve for it. If necessary, divide or multiply both sides of the equation to find the value of the unknown. Once you have determined the solution, check your work by substituting the value of the variable back into the original equation to ensure it satisfies both sides.
By following these steps carefully and practicing regularly, you will gain a deeper understanding of how to approach and solve equations with confidence.
Time Management for Your Mathematics Assessment
Effective time management is crucial when preparing for a mathematics assessment. With the right approach, you can maximize your study sessions and improve your performance. Planning ahead and allocating your time wisely helps ensure you cover all necessary material without feeling rushed or overwhelmed.
Strategies for Managing Your Time
Here are some practical strategies to help you manage your time during both preparation and the actual assessment:
- Create a Study Schedule: Organize your study sessions by breaking them into focused blocks of time. Set aside specific times for reviewing concepts, practicing problems, and taking breaks.
- Prioritize Difficult Topics: Start with the most challenging topics first, as these may require more time and attention. Address easier concepts later when you are more confident.
- Avoid Cramming: Last-minute studying is less effective and can increase anxiety. Instead, spread out your study sessions over several days or weeks to retain information better.
- Set Time Limits: During practice sessions, set a time limit for each question or problem. This helps you get used to pacing yourself during the actual test.
- Take Regular Breaks: Avoid long, uninterrupted study sessions. Take short breaks to recharge and stay focused, helping you maintain productivity over time.
Time Management on Test Day
When you sit down for your assessment, effective time management is just as important. Follow these tips to stay on track:
- Read Through the Test: Before you start solving problems, take a few minutes to scan the entire assessment. Identify the easier questions to tackle first and leave the more time-consuming ones for later.
- Allocate Time Per Section: Divide your available time by the number of sections or questions. Stick to the time limits and avoid spending too much time on one question.
- Stay Calm: If you encounter a difficult question, move on and return to it later. Staying calm under pressure helps you manage time more effectively.
By mastering time management, you can reduce stress and approach your mathematics assessment with a clear, focused mindset.
Key Mathematical Graphs to Know

Understanding the key types of graphs is essential for solving mathematical problems efficiently. Graphs represent the relationship between variables and provide a visual way of understanding mathematical concepts. By familiarizing yourself with these common graphs, you can gain insights into patterns and make solving equations more intuitive.
Common Types of Graphs

Here are the most important graphs you should know and their characteristics:
- Linear Graphs: These graphs represent straight lines and are used for equations of the form y = mx + b. The slope (m) and y-intercept (b) are key features of these graphs.
- Quadratic Graphs: Quadratic graphs form a parabola. They represent equations of the form y = ax² + bx + c. The graph shows symmetry and can open upwards or downwards depending on the value of “a”.
- Exponential Graphs: Exponential graphs represent equations where variables appear as exponents. They show rapid growth or decay and are often used in real-world applications like population growth.
- Absolute Value Graphs: These graphs create a “V” shape and represent equations like y = |x|. They show how a function behaves as the input value becomes positive or negative.
- Cubic Graphs: Cubic graphs show a curve with an S-shape and represent equations like y = ax³ + bx² + cx + d. These graphs can have one or two turning points.
Interpreting and Analyzing Graphs

Understanding the features of each graph is crucial for interpreting them correctly. Here are a few things to look for when analyzing graphs:
- Intercepts: Identify where the graph crosses the axes. The x-intercept and y-intercept provide important information about the values of the variables.
- Symmetry: Some graphs, like parabolas, have symmetry. Identifying the line of symmetry can help solve problems more efficiently.
- Slopes and Curves: Determine how steep a line is or how quickly a curve rises or falls. This can indicate rates of change in real-world situations.
By understanding these key graphs, you can improve your ability to analyze and solve mathematical problems that involve graphing and interpreting relationships between variables.
How to Approach Mathematical Proofs

Approaching mathematical proofs requires a structured method and logical thinking. A proof is essentially a step-by-step explanation that demonstrates the truth of a mathematical statement. Mastering the art of constructing a proof can make seemingly complex problems more manageable, as it helps you to break down the problem into clear and simple steps.
Steps to Solve Mathematical Proofs
To begin, follow these key steps when tackling a mathematical proof:
- Understand the Problem: Carefully read the problem and identify what needs to be proven. Understand the given information and what is being asked.
- Plan Your Approach: Decide on the type of proof that is most appropriate (direct, indirect, by contradiction, etc.). Planning will save time and guide your steps logically.
- State Assumptions: Clearly write down any assumptions or known facts that are given in the problem. These will form the foundation of your argument.
- Work Step-by-Step: Break the proof down into smaller steps. Work logically, showing how each step leads to the next. Keep each step clear and easy to follow.
- Conclude the Proof: Once you have logically derived the statement you were trying to prove, summarize your result, showing how it follows from the assumptions and steps taken.
Common Proof Techniques
There are several common techniques used to prove mathematical statements effectively:
- Direct Proof: Assume the statement is true and use logical steps to show that the conclusion follows from the assumptions.
- Proof by Contradiction: Assume the opposite of what you are trying to prove and show that it leads to a contradiction. This method demonstrates that the original statement must be true.
- Inductive Proof: Used when proving statements for all integers or for sequences. It involves showing the base case and then proving that if the statement holds for one case, it holds for the next.
- Proof by Counterexample: Provide a counterexample to disprove a statement. If you can show that one case does not hold, the statement is proven false.
By following these steps and using the appropriate techniques, you can successfully approach mathematical proofs and build logical arguments to demonstrate the truth of statements.
Solving Linear and Quadratic Equations
Solving mathematical equations involves finding the values that satisfy the given expressions. For both linear and quadratic types, each equation presents its own set of challenges, but with the right approach, they can be solved step by step. Understanding the methods used to tackle these equations is essential for mastering fundamental problem-solving skills in mathematics.
Solving Linear Equations
Linear equations are equations where the highest power of the variable is one. To solve these, the goal is to isolate the variable on one side of the equation. Here’s how to approach it:
- Step 1: Simplify both sides of the equation by combining like terms.
- Step 2: Move terms involving the variable to one side and constant terms to the other side.
- Step 3: Solve for the variable by dividing or multiplying both sides as necessary to isolate it.
- Step 4: Check the solution by substituting it back into the original equation to verify that both sides are equal.
Solving Quadratic Equations
Quadratic equations involve the square of the variable and are usually in the form of ax2 + bx + c = 0. There are several methods to solve these types of equations:
- Factoring: Express the equation as a product of binomials, then set each factor equal to zero and solve for the variable.
- Completing the Square: Rewrite the equation so that one side is a perfect square trinomial, then take the square root of both sides to solve for the variable.
- Using the Quadratic Formula: Apply the formula x = (-b ± √(b² – 4ac)) / 2a to solve for the variable. This method works for all quadratic equations.
By mastering these methods, you can confidently solve both linear and quadratic equations and build a solid foundation for more complex mathematical problems.
Practice Questions Explained
Practice problems are an essential part of mastering any mathematical topic. They help reinforce concepts, improve problem-solving skills, and build confidence. In this section, we will go through some common practice questions, break them down step by step, and explain how to approach them effectively.
Example 1: Solving Simple Linear Equations
Consider the equation 3x + 5 = 11. To solve for x, follow these steps:
- Step 1: Subtract 5 from both sides to isolate the term with the variable: 3x = 6.
- Step 2: Divide both sides by 3 to solve for x: x = 2.
This problem demonstrates a simple process of isolating the variable by performing inverse operations. The solution is x = 2.
Example 2: Solving a Quadratic Equation
Next, let’s consider a quadratic equation x2 – 5x + 6 = 0. To solve this, we can use factoring:
- Step 1: Factor the quadratic expression: (x – 2)(x – 3) = 0.
- Step 2: Set each factor equal to zero: x – 2 = 0 and x – 3 = 0.
- Step 3: Solve for x in each equation: x = 2 and x = 3.
This practice problem illustrates how factoring can be used to solve quadratic equations. The solutions are x = 2 and x = 3.
By breaking down problems into smaller, manageable steps, you can more easily understand and solve a wide range of mathematical questions. Keep practicing to improve your skills!
Mastering Word Problems in Mathematics
Word problems are a common yet challenging part of mathematical learning. They require not only understanding mathematical concepts but also translating real-world scenarios into mathematical language. The key to mastering these problems lies in breaking down the information, identifying the relevant data, and setting up an equation or process to find the solution. With practice and the right approach, solving word problems becomes a more straightforward task.
Here are some essential steps to effectively solve word problems:
- Step 1: Read the problem carefully and identify the important information. Pay attention to the numbers, variables, and any relationships mentioned.
- Step 2: Translate the words into mathematical expressions or equations. Look for keywords that indicate operations such as “sum,” “difference,” “product,” or “quotient.”
- Step 3: Solve the equation or simplify the expression according to the problem’s requirements.
- Step 4: Interpret the result in the context of the problem to ensure it makes sense.
By consistently following these steps, you can tackle word problems with confidence and accuracy. Let’s explore an example to see this approach in action:
Suppose a problem states: “The sum of twice a number and five is equal to 15. What is the number?”
- Step 1: Identify the unknown number and represent it with a variable, say x.
- Step 2: Translate the sentence into a mathematical equation: 2x + 5 = 15.
- Step 3: Solve the equation:
- Subtract 5 from both sides: 2x = 10.
- Divide by 2: x = 5.
- Step 4: The number is 5.
By applying these steps, the solution to the problem is found quickly and clearly. Keep practicing with various word problems, and soon you’ll be able to tackle even the most complex scenarios with ease.