
In this section, we will explore the essential topics that form the foundation of your math studies. By understanding the core principles, you will be better prepared to tackle various problems and strengthen your problem-solving skills. From basic equations to complex functions, mastering these areas is crucial for advancing in mathematics.
Solving problems step by step is a critical skill that helps you gain confidence and accuracy. Whether it’s simplifying expressions or finding solutions to unknowns, breaking down each task into smaller, manageable steps is key. The more you practice, the easier it becomes to approach unfamiliar challenges with confidence.
Strengthening your understanding of mathematical relationships will not only help you with assignments and exams but also develop logical thinking that can be applied to real-world situations. By reviewing these fundamental concepts, you can build a solid foundation that supports future learning and success in advanced topics.
Algebra 1 Review Answers
This section provides a comprehensive look at essential mathematical techniques and methods needed to solve key problems. The ability to manipulate equations, understand relationships between variables, and apply logical reasoning are critical to mastering this subject. By examining common problem types and their solutions, you can strengthen your skills and improve your understanding of the material.
One of the most important aspects of solving equations is identifying the correct approach. Whether working with simple expressions or more complex problems, recognizing the right steps can significantly ease the process. Practice will help you gain familiarity with different techniques, such as balancing equations, factoring, and applying mathematical rules.
By breaking down problems into smaller, manageable tasks, you can achieve greater accuracy and efficiency in finding solutions. The key to success lies in developing a clear strategy, ensuring you understand each part of the process, and applying your knowledge step by step. This methodical approach leads to better results and increased confidence in handling mathematical challenges.
Key Concepts in Algebra 1
This section highlights the fundamental principles that form the basis of understanding mathematical relationships and operations. Mastering these core ideas is crucial for progressing through more advanced topics and applying mathematical reasoning to solve real-world problems. The focus is on developing problem-solving strategies that can be applied to a variety of mathematical challenges.
Understanding how to manipulate expressions and equations is central to this area of study. Key techniques include simplifying terms, balancing equations, and working with variables to find unknown values. As you progress, you will encounter more complex problems that require a deeper understanding of these foundational rules and their applications.
Building fluency with these core concepts not only enhances mathematical abilities but also prepares you for future studies. The ability to recognize patterns, analyze relationships, and apply logical steps in solving problems is essential for achieving success in mathematics and beyond.
Understanding Algebraic Expressions
In this section, we focus on the fundamental building blocks used to represent mathematical relationships. These structures involve variables, constants, and operations that, when combined, express a variety of mathematical ideas. Developing a strong understanding of these elements is key to solving problems and manipulating equations effectively.
Components of an Expression
An expression typically consists of variables, numbers, and operations such as addition, subtraction, multiplication, and division. The challenge is to understand how these components interact and how to simplify or evaluate them. Recognizing the role of each element in an expression allows for a more intuitive approach when working through problems.
Simplifying and Manipulating Expressions

Once the basic components are identified, the next step is simplifying expressions by combining like terms and applying appropriate mathematical rules. This process helps streamline complex problems and makes it easier to solve for unknown values. Mastering these skills allows for more efficient problem solving in higher-level topics.
Solving Linear Equations

This section focuses on the methods used to solve equations where the unknown variable appears only to the first power. These types of problems are common and provide the foundation for more complex mathematical tasks. The goal is to find the value of the unknown that makes the equation true.
To solve these problems, one must isolate the variable by performing a series of operations on both sides of the equation. These operations–such as addition, subtraction, multiplication, and division–must maintain the equality between the two sides. By carefully applying these steps, the variable can be solved for.
Understanding the principles behind these steps ensures accuracy and efficiency when dealing with more challenging problems. With practice, you can quickly identify the necessary operations and solve linear equations with confidence.
Graphing Lines and Slopes
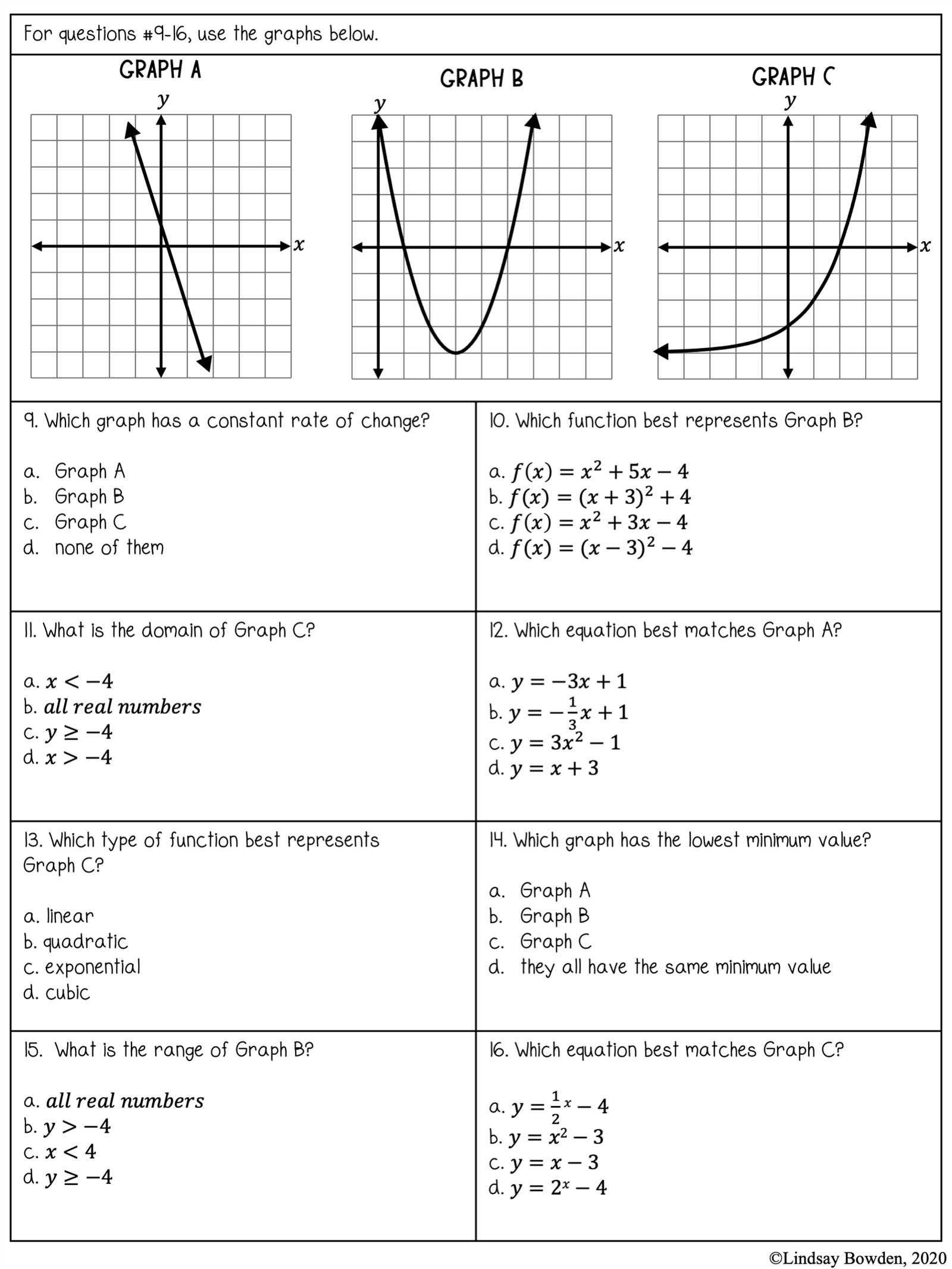
This section explores the process of representing relationships between variables on a coordinate plane. By graphing lines, we can visually interpret how two quantities change in relation to each other. Understanding how to plot these lines and determine their steepness is crucial for solving real-world problems involving rates of change.
Plotting Points and Drawing Lines
To graph a line, you first need to plot points that satisfy the equation. These points can then be connected to form a straight line. Identifying key points, such as intercepts, can make the process easier and more intuitive. A graph provides a visual representation of the equation, allowing for a deeper understanding of how the variables interact.
Understanding Slope

The slope of a line indicates its steepness and direction. It is calculated by the ratio of the vertical change to the horizontal change between two points on the line. This value gives important insight into the relationship between the variables, whether they increase, decrease, or remain constant. Mastering slope calculation is essential for interpreting and solving linear equations effectively.
Solving Quadratic Equations
This section covers methods used to solve equations where the variable is squared. These types of problems often arise in various fields, from physics to finance, and provide insight into complex relationships. Solving these equations involves finding the values of the variable that satisfy the equation, which can be done through several techniques.
Factoring and Solving by Roots

One approach to solving such equations is factoring, where the equation is expressed as the product of two binomials. If factored correctly, setting each factor equal to zero allows for finding the solutions. This method is particularly effective when the equation is factorable and leads to simpler calculations.
Using the Quadratic Formula
Another method is the quadratic formula, which provides a solution for any quadratic equation. By plugging the values from the equation into the formula, you can directly calculate the roots, even if factoring is not possible. This formula, x = (-b ± √(b² – 4ac)) / 2a, is a powerful tool for finding exact solutions.
Understanding both methods enables you to approach quadratic equations with flexibility and confidence, ensuring you can tackle any type of problem efficiently.
Factoring Polynomials Efficiently

This section explores methods for breaking down complex expressions into simpler factors. Factoring polynomials involves identifying common terms and relationships that allow the expression to be rewritten as the product of two or more binomials. Mastering this process is essential for simplifying equations and solving a variety of mathematical problems.
One of the most common techniques is factoring by grouping, which involves rearranging terms so that pairs of terms can be factored separately. Another method is recognizing special patterns, such as the difference of squares or perfect square trinomials, which can be quickly factored with known formulas. By practicing these strategies, you can factor polynomials more quickly and accurately, making complex problems more manageable.
Efficient factoring relies on experience and the ability to recognize patterns. With consistent practice, the process becomes faster, allowing you to handle larger expressions with confidence.
Working with Rational Expressions
This section focuses on manipulating expressions that involve ratios of polynomials. These types of expressions are common in various mathematical applications, and understanding how to simplify, multiply, and divide them is essential for solving more complex problems. The goal is to work with these expressions in a way that makes them easier to handle and solve.
Simplifying Rational Expressions
One of the key steps in working with these expressions is simplifying them. This involves canceling out common factors from the numerator and denominator. By factoring both parts and identifying shared terms, you can reduce the expression to its simplest form, making it easier to perform other operations.
Multiplying and Dividing Rational Expressions
Multiplying and dividing these expressions follows a straightforward process. When multiplying, simply multiply the numerators and denominators separately, and then simplify if possible. For division, multiply by the reciprocal of the second expression. Remember to factor and cancel terms whenever possible to avoid unnecessary complexity.
By mastering these techniques, you can effectively solve problems involving rational expressions and gain a deeper understanding of their applications in different mathematical contexts.
Understanding Systems of Equations
This section explores the process of solving multiple equations simultaneously. Systems of equations consist of two or more equations with the same set of variables, and the objective is to find values for those variables that satisfy all the equations in the system. This is an essential skill for tackling a wide range of mathematical problems, from simple calculations to more complex real-world scenarios.
There are various methods for solving systems of equations, each useful in different situations:
- Substitution Method: Solve one equation for one variable, then substitute that expression into the other equation.
- Elimination Method: Add or subtract the equations to eliminate one variable, making it easier to solve for the other.
- Graphing Method: Plot both equations on the same coordinate plane and find the point where the lines intersect, representing the solution.
Each method has its advantages, depending on the complexity of the equations involved. Understanding when and how to apply each technique is key to solving systems efficiently.
Using Inequalities in Algebra
This section focuses on how to work with expressions that describe relationships where values are not necessarily equal but fall within a certain range. Inequalities are used to express situations where one quantity is greater than, less than, or not equal to another, making them essential tools for solving a variety of mathematical problems and real-life scenarios.
There are several methods to solve and manipulate inequalities:
- Solving Linear Inequalities: Similar to equations, but you must reverse the inequality symbol when multiplying or dividing by a negative number.
- Graphing Inequalities: Representing the solutions on a number line or coordinate plane to visualize the range of possible values.
- Compound Inequalities: Involving two inequalities connected by “and” or “or” to describe more complex relationships.
Working with inequalities requires careful attention to the rules for manipulating them, especially when dealing with negative numbers or compound conditions. Understanding how to represent these relationships graphically or algebraically provides a powerful way to analyze and solve problems.
Exploring Absolute Value Equations
This section delves into equations that involve the absolute value of a variable. These equations represent situations where the distance of a number from zero is important, regardless of direction. Solving these types of problems requires understanding that the absolute value expression can have two possible solutions: one positive and one negative.
When solving absolute value equations, the goal is to isolate the absolute value expression and then split the equation into two separate cases, based on the definition of absolute value. This leads to two distinct equations that can be solved individually:
- Positive Case: Solve the equation as if the expression inside the absolute value is positive.
- Negative Case: Solve the equation as if the expression inside the absolute value is negative, effectively removing the absolute value symbol.
It is important to check your solutions after solving, as some values may not satisfy the original equation due to the nature of absolute value. Mastering these types of equations opens the door to solving more complex mathematical problems involving distance, magnitude, and other real-world applications.
Mastering Exponents and Powers

This section focuses on understanding the rules and applications of exponents and powers. These concepts are crucial for simplifying expressions and solving complex problems in various branches of mathematics. Mastering exponents allows you to work efficiently with large numbers and solve problems involving repeated multiplication.
Exponents represent the number of times a base is multiplied by itself. Knowing how to apply the basic exponent rules helps to simplify expressions and makes it easier to perform operations on numbers involving powers. The following table summarizes the key exponent laws:
| Exponent Rule | Description | Example |
|---|---|---|
| Product Rule | When multiplying powers with the same base, add the exponents. | ( a^m times a^n = a^{m+n} ) |
| Quotient Rule | When dividing powers with the same base, subtract the exponents. | ( frac{a^m}{a^n} = a^{m-n} ) |
| Power of a Power | When raising a power to another power, multiply the exponents. | ( (a^m)^n = a^{m times n} ) |
| Zero Exponent Rule | Any base raised to the power of zero equals 1. | ( a^0 = 1 ) |
By applying these rules, you can simplify complex expressions and solve equations more easily. Understanding how to work with exponents is a fundamental skill for tackling higher-level mathematical problems.
Simplifying Radical Expressions

This section covers the process of simplifying expressions that involve roots, a common operation in many mathematical problems. Simplifying these expressions is essential for making complex problems more manageable and for solving equations efficiently. By reducing roots to their simplest form, we can avoid unnecessary complications and gain a clearer understanding of the problem at hand.
To simplify such expressions, the goal is to break them down into smaller, easier-to-handle components. Here are some key steps involved:
- Identifying Perfect Squares: Look for square numbers or factors that can simplify the expression. For example, ( sqrt{36} = 6 ).
- Factoring the Radicand: Factor the number inside the root and separate the perfect squares from the non-perfect squares. For instance, ( sqrt{18} = sqrt{9 times 2} = 3sqrt{2} ).
- Rationalizing Denominators: If there is a radical in the denominator, multiply both the numerator and denominator by a suitable value to eliminate the root in the denominator.
By following these steps, you can simplify complex radical expressions, making them easier to work with in equations and calculations. Mastering this technique will help you handle a wide range of problems involving square roots, cube roots, and higher-order radicals.
Analyzing Functions and Their Graphs
This section delves into the study of relationships between variables and how these relationships are represented visually. A function is a rule that assigns each input exactly one output, and understanding how to interpret these rules is essential for solving problems and making predictions. By analyzing the graphs of these relationships, you can gain insights into the behavior of the function and how it responds to different inputs.
When analyzing a function, the goal is to understand its characteristics and the information the graph conveys. Key aspects to focus on include:
- Domain and Range: Identify the possible values for the input (domain) and the corresponding output values (range).
- Intercepts: Determine where the graph crosses the x-axis (x-intercept) and y-axis (y-intercept).
- Increasing and Decreasing Intervals: Find the parts of the graph where the function is rising or falling.
- Asymptotes: Investigate horizontal, vertical, or oblique lines that the graph approaches but never touches.
- Symmetry: Check for symmetry about the y-axis, x-axis, or origin, which can help simplify analysis.
By analyzing these features, you can gain a deeper understanding of how a function behaves across different values. This skill is crucial for solving equations and interpreting data in fields ranging from economics to engineering.
Solving Word Problems in Algebra
Word problems present mathematical challenges in real-world contexts, requiring the translation of textual information into mathematical expressions and equations. These problems often seem complex at first glance, but with the right approach, they can be simplified and solved step by step. The key to success lies in understanding the problem’s structure and identifying what is being asked.
Here are some effective strategies for solving these types of problems:
- Read the Problem Carefully: Understand the context and identify the important information provided. Take note of any quantities, relationships, and conditions mentioned in the text.
- Define Variables: Assign variables to the unknowns in the problem. This helps organize the information and create equations that represent the problem.
- Translate Words into Equations: Convert the given information into mathematical expressions. Look for key words like “sum,” “difference,” “product,” or “quotient” to guide your translation.
- Set Up the Equation: Based on the translation, write an equation that models the situation. Ensure that all relationships between quantities are accurately represented.
- Solve the Equation: Use algebraic techniques such as addition, subtraction, multiplication, division, or factoring to solve the equation for the unknown variable.
- Check Your Solution: Once a solution is found, substitute the value back into the context of the problem to ensure it makes sense and satisfies all conditions.
By following these steps, you can systematically break down word problems and apply the correct mathematical methods to find solutions. Practicing these techniques will help you build confidence in solving a wide range of real-world problems.
Tips for Algebra 1 Test Preparation
Preparing for a mathematics exam can be a challenging but rewarding experience. Success in these assessments requires both understanding key concepts and practicing problem-solving skills. The process involves reviewing material, honing strategies, and ensuring that you’re comfortable with the types of questions that may appear on the test. With the right approach, you can enhance your performance and build the confidence needed to excel.
Effective Study Techniques

To maximize your preparation, focus on the following strategies:
- Review Key Concepts: Revisit important topics and make sure you understand the foundational principles. This includes working through examples of equations, graphing techniques, and functions.
- Practice Regularly: The more problems you solve, the better you’ll grasp the material. Make sure to attempt a variety of problems to reinforce your knowledge.
- Use Flashcards: Create flashcards for formulas, rules, and terms to improve recall during the test.
- Work in Study Groups: Collaborating with peers can help you understand difficult concepts and offer new perspectives on problem-solving methods.
- Take Timed Quizzes: Simulate test conditions by timing yourself while taking practice tests. This will help you manage time during the actual exam.
Test Day Tips

On the day of the test, be sure to:
- Arrive Early: Give yourself time to settle in and relax before the test starts. Stress can affect your performance, so try to stay calm.
- Read Questions Carefully: Take the time to understand what each question is asking. Look for keywords and pay attention to any specific instructions.
- Show Your Work: Even if you’re confident in your answers, write out your calculations. This can help you avoid mistakes and make it easier to spot errors if they occur.
Study Schedule and Resources
Creating a structured study plan is essential for success. Here’s an example schedule to help organize your time:
| Day | Study Focus |
|---|---|
| Day 1 | Review linear equations and graphing techniques. |
| Day 2 | Practice solving systems of equations and inequalities. |
| Day 3 | Work on quadratic equations and factoring methods. |
| Day 4 | Take a timed practice test to simulate the exam environment. |
| Day 5 | Review areas of difficulty and rework missed problems. |
By following these strategies and maintaining a focused study routine, you’ll be well-prepared for the test and ready to tackle any challenges that come your way.
Common Mistakes to Avoid in Algebra
When solving mathematical problems, certain pitfalls are often encountered that can lead to errors and confusion. These mistakes may stem from misunderstandings of fundamental principles, careless calculations, or misinterpreting instructions. Recognizing and avoiding these common errors can significantly improve problem-solving accuracy and boost confidence when tackling mathematical exercises.
One of the most frequent mistakes is neglecting to properly follow the order of operations. This rule dictates the sequence in which operations should be carried out, and skipping a step can lead to incorrect results. Additionally, misapplying formulas or not simplifying expressions fully can result in incorrect solutions, particularly in more complex problems.
Another common issue is failing to account for negative signs. Whether adding, subtracting, multiplying, or dividing, missing a negative can drastically alter the outcome. In equations, this mistake can sometimes lead to completely wrong answers, especially when variables or constants involve negative numbers.
Finally, be cautious when dealing with fractions or decimals. It’s easy to make mistakes in simplification or conversion, especially when performing multiple steps. Always double-check operations involving fractions, and ensure the correct application of rules for multiplying or dividing fractions.
By staying mindful of these potential errors and actively working to avoid them, you’ll develop a stronger understanding and greater proficiency in solving mathematical problems efficiently.