
In this guide, we will explore essential topics in mathematics that are crucial for successfully navigating the final stage of your coursework. Focusing on problem-solving techniques, this resource will provide you with the tools and strategies needed to approach complex questions with confidence. Each section breaks down core concepts, allowing you to reinforce your understanding and tackle a variety of challenges effectively.
Whether you’re looking to refresh your memory on basic principles or dive deeper into more advanced methods, this guide offers a structured path to help you prepare. By examining common pitfalls and presenting clear, step-by-step solutions, you will be well-equipped to face any mathematical challenge that arises.
Stay focused, practice regularly, and make use of the strategies outlined here to achieve the best possible results. Mastering these skills will not only help you succeed but also build a strong foundation for future mathematical endeavors.
Algebra 1 Spring Final Exam Review Answers
This section is designed to provide the essential tools and methods needed to tackle a variety of mathematical challenges. The focus will be on reinforcing key concepts, breaking down problem-solving strategies, and highlighting common errors to avoid. With a structured approach, you’ll be equipped to work through problems with confidence and efficiency.
Key Concepts to Focus On
- Understanding linear equations and their solutions
- Mastering factoring techniques for polynomials
- Working with inequalities and graphing solutions
- Solving systems of equations step-by-step
- Grasping the fundamentals of quadratic functions
- Interpreting and solving word problems accurately
Effective Problem-Solving Strategies
- Break down complex problems into simpler steps
- Double-check calculations to avoid common errors
- Use graphical representations for visualizing solutions
- Practice different methods for solving equations
- Review key formulas regularly for quick recall
By focusing on these areas and practicing regularly, you will be well-prepared to approach even the most challenging questions with a clear strategy and solid understanding.
Key Concepts for Algebra 1 Finals
Mastering the fundamental ideas in mathematics is essential for success in any assessment. This section highlights the core concepts that will help you strengthen your understanding and tackle a wide range of problems. A solid grasp of these topics will not only prepare you for the test but also ensure that you have the foundational skills to progress in more advanced mathematical studies.
| Concept | Description | Key Skills |
|---|---|---|
| Linear Equations | Solving equations with one variable | Identifying solutions, graphing lines |
| Factoring Polynomials | Breaking down expressions into simpler components | Recognizing common factors, factoring quadratics |
| Inequalities | Solving and graphing inequalities | Interpreting solutions, shading regions on graphs |
| Quadratic Functions | Understanding the properties of quadratic equations | Factoring quadratics, using the quadratic formula |
| Systems of Equations | Solving sets of linear equations | Substitution, elimination methods |
Focusing on these core concepts will give you the confidence to solve a variety of problems, as well as the skills needed to tackle more complex topics in the future. Review each area, practice consistently, and refine your problem-solving strategies to ensure success.
Step-by-Step Solutions for Algebraic Problems
To solve mathematical problems effectively, it is essential to break them down into manageable steps. By following a clear, logical approach, you can simplify complex expressions and arrive at the correct solution. This section provides detailed methods for solving various types of problems, from basic equations to more advanced expressions.
Step 1: Begin by identifying the problem type. Whether it’s an equation or an expression, recognizing the structure helps determine the best approach. Focus on isolating the unknown variable or simplifying the terms.
Step 2: Apply the appropriate operations. This may involve addition, subtraction, multiplication, or division, depending on the equation. Be consistent and use inverse operations when necessary to maintain balance on both sides.
Step 3: Simplify the expression step by step. Look for opportunities to combine like terms, factor expressions, or eliminate unnecessary parts. This will make the equation easier to solve and will reveal the solution more clearly.
Step 4: Check your solution. After reaching a result, plug the value back into the original equation to verify its correctness. This ensures that the solution is valid and that no mistakes were made during the process.
By following these steps for each problem, you will develop a structured approach to solving mathematical challenges. Practice regularly, and soon you’ll be able to solve even the most difficult problems with ease and precision.
Common Mistakes to Avoid on the Exam
When preparing for a mathematical assessment, it’s important to be aware of common pitfalls that can hinder your performance. These errors often occur due to rushing, misinterpreting problems, or overlooking essential details. Recognizing and avoiding these mistakes will help you perform better and ensure you approach each question with confidence.
Common Errors in Problem Solving
- Failing to read the question carefully
- Misplacing signs (positive/negative) in equations
- Forgetting to distribute terms correctly in expressions
- Skipping steps or trying to solve too quickly
- Using incorrect formulas or methods for certain problem types
Conceptual Mistakes to Watch For
- Confusing different types of equations (linear vs. quadratic)
- Misunderstanding the relationship between variables in a system
- Incorrectly graphing equations or interpreting slopes
- Ignoring restrictions on the variable in rational expressions
- Overlooking possible extraneous solutions in certain equations
By being aware of these typical errors and taking your time to avoid them, you can ensure a smoother experience and achieve better results during the test.
Important Formulas for Algebra 1 Exam
Having a solid understanding of key mathematical formulas is crucial when solving problems efficiently. This section highlights the most essential equations and expressions that will help you tackle a wide variety of challenges. By memorizing and applying these formulas, you will be better prepared for any question that arises.
Essential Equations and Formulas
- Linear Equation: y = mx + b (Slope-intercept form)
- Quadratic Equation: x = (-b ± √(b² – 4ac)) / 2a (Quadratic formula)
- Point-Slope Form: y – y₁ = m(x – x₁)
- Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²)
- Pythagorean Theorem: a² + b² = c²
- Factoring Formula: (a + b)(a – b) = a² – b²
Important Properties to Remember
- Distributive Property: a(b + c) = ab + ac
- Commutative Property of Addition: a + b = b + a
- Associative Property of Multiplication: (a * b) * c = a * (b * c)
- Zero Product Property: if ab = 0, then a = 0 or b = 0
Remembering and applying these formulas will greatly improve your problem-solving abilities and give you the confidence needed to approach each task methodically and accurately.
Understanding Linear Equations and Functions
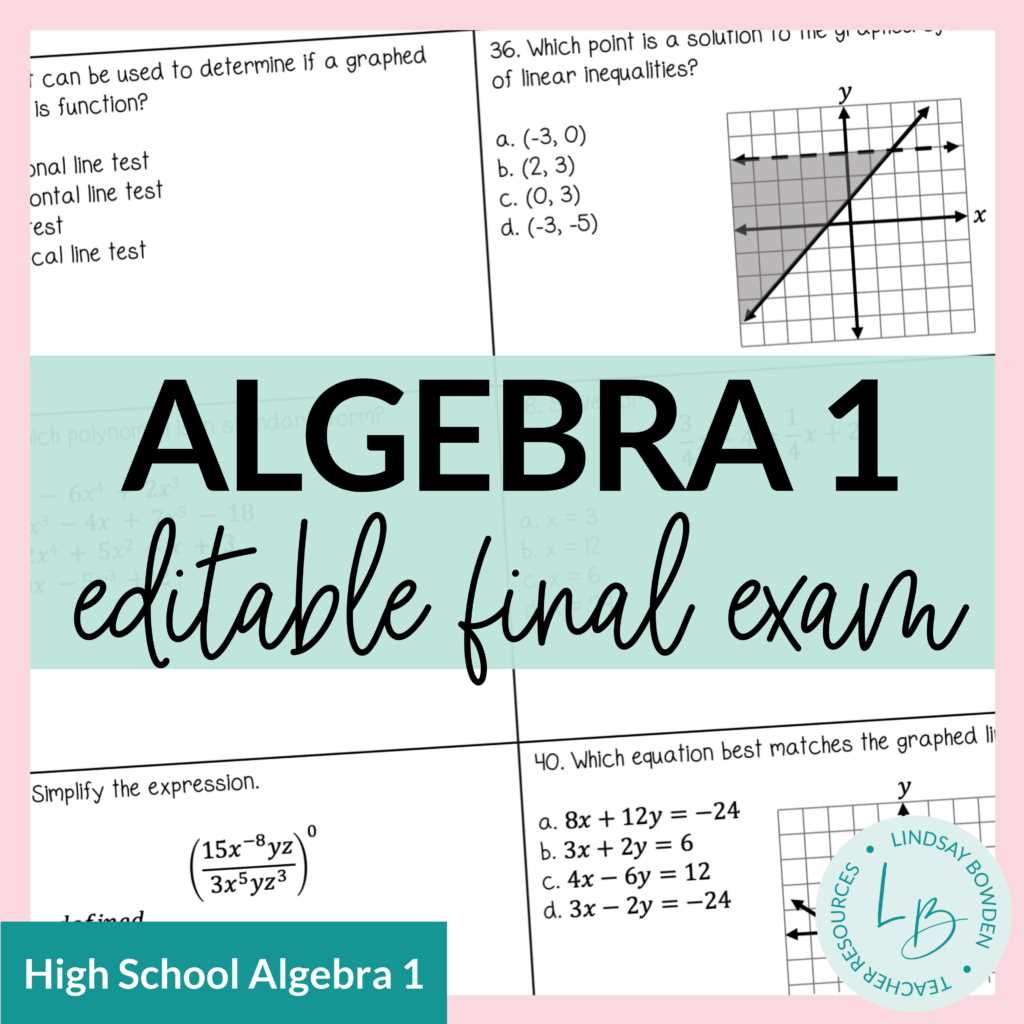
Linear equations and functions are fundamental concepts in mathematics, essential for solving a wide range of problems. These expressions describe relationships between variables and can be represented graphically as straight lines. A clear understanding of how to manipulate and interpret these equations is key to mastering more complex topics.
Key Features of Linear Equations
- Slope: The rate at which one variable changes in relation to another. It is calculated as m = (y₂ – y₁) / (x₂ – x₁).
- Y-intercept: The point where the line crosses the y-axis, denoted as b in the equation y = mx + b.
- Standard Form: Linear equations can also be written in the form Ax + By = C, where A, B, and C are constants.
- Point-Slope Form: Another way to express a line is y – y₁ = m(x – x₁), where (x₁, y₁) is a known point on the line.
How to Solve and Graph Linear Functions
- Solve for the Variable: Isolate the variable of interest (typically y) on one side of the equation.
- Plot Points: Use the slope and y-intercept to plot key points on the coordinate plane, then draw a straight line through them.
- Graphing: Once the equation is simplified, graphing involves marking the y-intercept and using the slope to find additional points.
- Finding Solutions: Substitute different values for x to find corresponding y values, or vice versa, to solve the equation.
Mastering linear equations and their graphing techniques will give you a solid foundation for working with more advanced functions and problem-solving strategies. Practice and familiarity with these methods will allow you to approach a variety of questions with confidence and accuracy.
Graphing Techniques for Algebraic Equations

Graphing is an essential skill when solving mathematical problems that involve relationships between variables. By visually representing equations on a coordinate plane, you can better understand how different values interact and identify key features such as slopes and intercepts. This section covers essential techniques for graphing equations effectively and interpreting their results.
Steps for Graphing Linear Equations
- Identify the equation type: Determine if the equation is in slope-intercept form y = mx + b, standard form Ax + By = C, or another variation.
- Find the y-intercept: The value of b in the equation represents the point where the line crosses the y-axis. Plot this point on the graph.
- Calculate the slope: The slope m indicates the rise over run. Use it to determine how the line increases or decreases as you move along the x-axis.
- Plot additional points: Using the slope, find other points on the line and plot them on the coordinate plane.
- Draw the line: Connect the points with a straight line, extending in both directions.
Graphing Other Types of Equations
- Quadratic Functions: Graph parabolas by identifying the vertex, axis of symmetry, and using a table of values to plot key points.
- Systems of Equations: To graph a system of equations, plot the lines or curves of each equation and identify the point where they intersect. This point is the solution.
- Inequalities: Graphing inequalities involves shading the region that satisfies the inequality. The line should be solid for ≤ or ≥ and dashed for .
With practice, graphing becomes an invaluable tool for solving and visualizing various mathematical problems. By understanding these techniques, you’ll be able to interpret equations more easily and approach problems with confidence.
Solving Quadratic Equations with Ease
Quadratic equations are a common type of problem that requires understanding of several solving techniques. These equations, which involve terms up to the second degree, can be solved through various methods, each suited for different situations. Mastering these methods will allow you to tackle problems quickly and accurately, regardless of the specific form the equation takes.
Methods for Solving Quadratic Equations
- Factoring: This method involves rewriting the equation as a product of two binomials and solving for the variable.
- Completing the Square: This technique transforms the quadratic into a perfect square trinomial, making it easy to solve by taking square roots.
- Quadratic Formula: The most general method for solving any quadratic equation is by using the formula x = (-b ± √(b² – 4ac)) / 2a.
Example of Solving Using the Quadratic Formula
Let’s consider the equation 2x² – 4x – 6 = 0. To solve it using the quadratic formula, we follow these steps:
| Step | Action |
|---|---|
| 1 | Identify coefficients: a = 2, b = -4, c = -6 |
| 2 | Substitute into the quadratic formula: x = (-(-4) ± √((-4)² – 4(2)(-6))) / 2(2) |
| 3 | Simplify: x = (4 ± √(16 + 48)) / 4 |
| 4 | Continue simplifying: x = (4 ± √64) / 4 |
| 5 | Find the square root: x = (4 ± 8) / 4 |
| 6 | Calculate the two solutions: x = (4 + 8) / 4 = 3 or x = (4 – 8) / 4 = -1 |
By using the quadratic formula, we find two solutions: x = 3 and x = -1. This method works for any quadratic equation, regardless of whether the equation factors neatly or not.
With consistent practice, solving quadratic equations will become an easier task, allowing you to confidently solve more complex problems.
Tips for Working with Inequalities
Solving inequalities is a crucial skill in mathematics, allowing you to understand and compare different values based on their relationships. Unlike equations, inequalities express a range of possible solutions rather than a single exact value. This section will provide helpful strategies to solve and interpret inequalities effectively.
Key Strategies for Solving Inequalities
- Isolate the Variable: Just like solving an equation, the goal is to get the variable on one side of the inequality. Start by performing the same operations on both sides.
- Reverse the Inequality Sign: If you multiply or divide by a negative number, you must flip the inequality symbol. This is a common mistake to avoid.
- Check the Solution: Once you have found the solution, plug it back into the original inequality to verify that it satisfies the condition.
- Graph the Solution: When solving inequalities, it can be helpful to represent the solution on a number line to clearly visualize the range of values that satisfy the inequality.
Common Types of Inequalities
- Linear Inequalities: These are inequalities that involve linear expressions and can be solved similarly to linear equations.
- Compound Inequalities: These involve two inequalities that are joined by the word “and” or “or,” requiring careful analysis of the combined solution set.
- Inequalities Involving Absolute Values: These require breaking the inequality into two separate cases: one for the positive value and one for the negative value.
By following these tips and practicing different types of inequalities, you will build confidence in solving them quickly and accurately, laying the foundation for more advanced problem-solving techniques.
Factoring Strategies for Algebraic Expressions
Factoring is a powerful technique used to simplify algebraic expressions and solve equations more efficiently. It involves breaking down a complex expression into simpler components, making it easier to identify solutions or manipulate further. Mastering various factoring strategies can significantly improve your ability to handle different types of algebraic problems.
Common Factoring Techniques
- Factoring Out the Greatest Common Factor (GCF): Start by identifying the greatest common factor of all terms in the expression and factor it out. This simplifies the expression, making it easier to factor further.
- Factoring Trinomials: For quadratic expressions in the form ax² + bx + c, look for two numbers that multiply to ac and add up to b. Use these numbers to break up the middle term and factor by grouping.
- Difference of Squares: Expressions in the form a² – b² can be factored as (a + b)(a – b). This is a quick and straightforward method for recognizing and factoring these types of expressions.
- Perfect Square Trinomials: Expressions like a² ± 2ab + b² can be factored as (a ± b)². Recognizing this pattern helps simplify more complicated expressions.
Example of Factoring a Quadratic Expression
Consider the quadratic expression 6x² + 11x – 35. To factor it, follow these steps:
- Identify the product of the first and last coefficients: 6 * -35 = -210.
- Find two numbers that multiply to -210 and add up to 11. These numbers are 21 and -10.
- Rewrite the middle term: 6x² + 21x – 10x – 35.
- Group terms: (6x² + 21x) – (10x + 35).
- Factor each group: 3x(2x + 7) – 5(2x + 7).
- Factor out the common binomial: (2x + 7)(3x – 5).
By practicing these strategies and recognizing patterns, you can improve your factoring skills and solve algebraic expressions more efficiently.
Exponents and Polynomials Review
Understanding how to work with exponents and polynomials is essential for solving a wide range of mathematical problems. Exponents represent repeated multiplication of a number, while polynomials are expressions made up of multiple terms. Mastering the rules for both helps simplify complex expressions and makes problem-solving more efficient.
When working with exponents, it’s important to remember key rules, such as the product of powers rule, the power of a power rule, and the power of a product rule. These allow you to simplify expressions involving exponents more easily. For polynomials, you’ll need to be familiar with operations like addition, subtraction, multiplication, and division, as well as factoring techniques that help break down larger expressions.
By reviewing these concepts and practicing problems, you’ll be better equipped to handle various mathematical tasks that involve exponents and polynomials. Whether simplifying expressions or solving equations, a solid understanding of these topics is crucial for success.
Tips for Word Problems on the Exam
Word problems can often seem daunting, but with the right approach, they can be broken down into manageable steps. The key is to translate the given information into mathematical expressions and solve them systematically. Understanding how to identify relevant details and apply appropriate strategies will help you solve these problems with confidence.
Steps to Approach Word Problems
- Read Carefully: Start by reading the problem thoroughly. Pay attention to all the details, including numbers, units, and keywords that indicate mathematical operations like “sum,” “difference,” “product,” or “quotient.”
- Identify Variables: Assign variables to the unknowns in the problem. For example, let x represent the number of items or the unknown value you’re trying to find.
- Translate into Equations: Convert the word problem into one or more equations based on the relationships described in the text. Use operations like addition, subtraction, multiplication, or division as indicated by the problem.
- Check Units and Dimensions: Ensure that you’re using the correct units throughout the problem. If necessary, convert units to match the required answer.
- Solve Step-by-Step: Solve the equation or system of equations one step at a time, and keep track of intermediate calculations to avoid mistakes.
Common Mistakes to Avoid
- Misinterpreting Keywords: Words like “increased by” or “reduced by” may seem similar but can indicate different operations. Be careful not to confuse them.
- Skipping Units: Forgetting to track or convert units can lead to incorrect answers, especially when dealing with measurements or rates.
- Overcomplicating the Problem: Simplify the situation by focusing on the key points and avoid getting lost in unnecessary details. Sometimes, the simplest method is the best.
By following these steps and practicing regularly, you’ll improve your ability to solve word problems effectively and efficiently, helping you tackle these types of questions with ease.
Solving Systems of Equations Effectively
When faced with multiple equations that involve the same variables, solving these systems can seem challenging at first. However, by using systematic methods, you can efficiently find the values that satisfy all the equations simultaneously. Whether through substitution, elimination, or graphing, each method has its strengths depending on the problem at hand.
The substitution method involves solving one equation for one variable and then substituting that expression into the other equation. This allows you to reduce the system to a single equation with one variable, which is easier to solve. On the other hand, the elimination method involves adding or subtracting equations to eliminate one variable, making it possible to solve for the remaining variable. Both approaches are highly effective when applied correctly.
Practice with these techniques will improve your problem-solving efficiency and help you navigate through systems of equations with confidence. Understanding when to use each method will allow you to choose the most efficient approach for the task at hand.
Exploring Rational Expressions and Equations
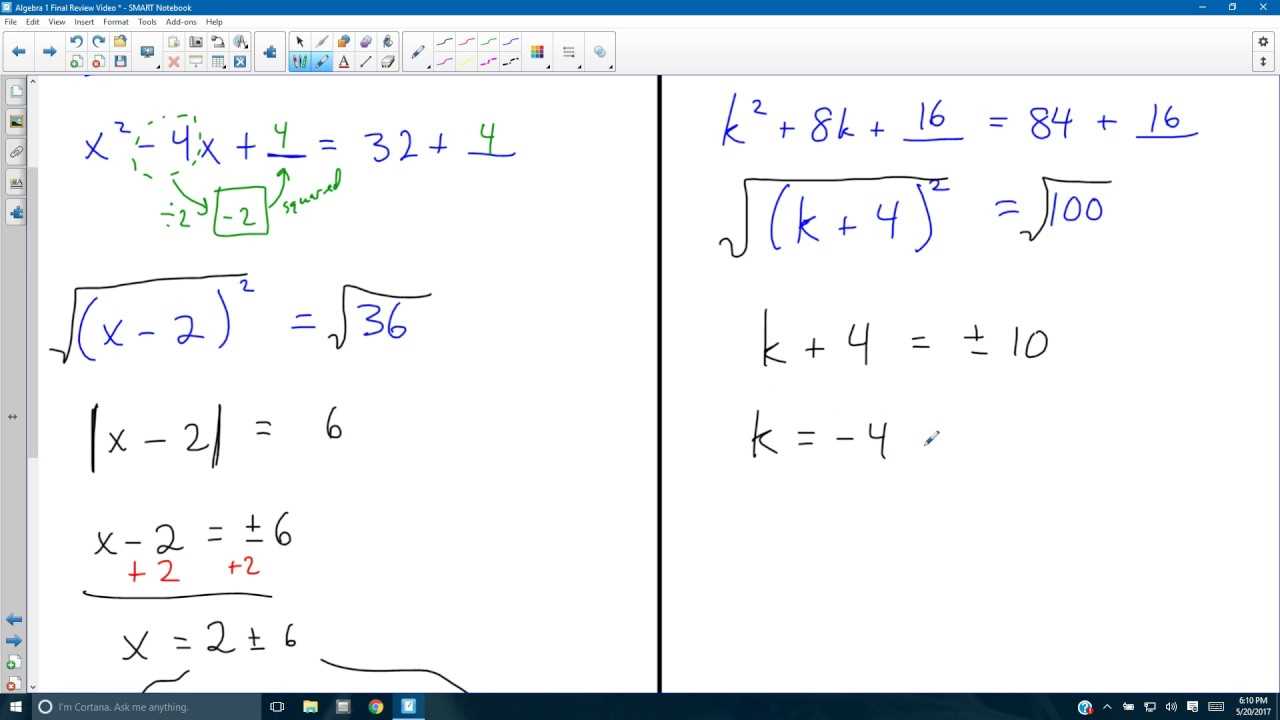
Rational expressions and equations are mathematical constructs that involve fractions where both the numerator and the denominator are polynomials. Understanding how to manipulate these expressions is essential for solving a variety of problems in advanced mathematics. Simplifying, multiplying, dividing, and solving rational equations all require a strong grasp of these concepts.
Simplifying Rational Expressions
To simplify a rational expression, start by factoring both the numerator and the denominator. Look for common factors between them, and cancel out any factors that appear in both places. This can make the expression simpler and more manageable. Always check for restrictions in the original expression, as certain values might make the denominator zero, which would make the expression undefined.
Solving Rational Equations
When solving equations that involve rational expressions, the goal is to eliminate the fractions by multiplying through by the least common denominator (LCD). This step clears the denominators, transforming the equation into a more straightforward linear or quadratic form. Be sure to check for extraneous solutions by substituting your solutions back into the original equation.
Rational expressions and equations offer powerful tools for solving real-world problems, but they require careful attention to detail. By practicing the techniques of simplification and solving, you’ll be better prepared to handle even the most complex rational equations.
Understanding Radical Expressions and Functions
Radical expressions and functions involve roots, such as square roots or cube roots, and play a crucial role in understanding the behavior of certain mathematical relationships. These expressions can be simplified and manipulated to solve equations, model real-world situations, or express geometric relationships. Learning how to work with these types of expressions will enhance your problem-solving skills in various areas of mathematics.
A radical expression includes a root symbol, and the number inside the root is called the radicand. The simplest form is the square root, but higher roots like cube roots or fourth roots can also be encountered. When simplifying radical expressions, it’s essential to factor the radicand and look for perfect squares or cubes that can be simplified. This process can make calculations easier and allow for more efficient problem-solving.
Operations with Radical Expressions
Just like with regular algebraic expressions, you can perform operations with radical expressions such as addition, subtraction, multiplication, and division. However, there are special rules for each operation when dealing with roots:
- Addition/Subtraction: You can only combine terms with the same root and radicand, known as like terms.
- Multiplication/Division: Multiply or divide the coefficients and then multiply or divide the radicands, simplifying as necessary.
Graphing Radical Functions
Graphing radical functions requires an understanding of how the function behaves as the variable changes. The domain of a radical function is restricted to ensure that the radicand does not result in an undefined value (such as a negative number inside a square root in the real number system). The graph of a radical function often has a distinct shape, depending on whether it’s a square root, cube root, or other types of roots.
| Radical Expression | Simplified Form | Domain Restrictions |
|---|---|---|
| √(x + 4) | √(x + 4) | x ≥ -4 |
| ³√(x – 1) | ³√(x – 1) | No restrictions |
By practicing simplification, performing operations, and graphing radical expressions, you can build a deeper understanding of how they function in mathematical equations and real-world applications.
Reviewing Algebraic Functions and Graphs
Understanding mathematical functions and their graphical representations is essential in mastering the relationships between variables. Functions describe how one quantity depends on another, and the graph provides a visual representation of this relationship. Mastery of functions and graphs allows for solving real-world problems and making predictions based on mathematical models.
In this section, we will revisit key concepts related to functions, including how to interpret and sketch their graphs, identify different types of functions, and analyze the properties that define them, such as domain, range, intercepts, and behavior at extremes. Each function has specific characteristics that influence its graph’s shape and how it behaves when values of the independent variable change.
Understanding Function Types
Functions can be classified into various types, each with distinct properties and graphing behaviors. The most common types include:
- Linear Functions: These are characterized by constant rates of change and produce straight-line graphs.
- Quadratic Functions: Represented by parabolas, these functions have a variable rate of change and are symmetric about a central axis.
- Cubic Functions: These produce graphs with one or more turning points and can change direction in multiple ways.
- Exponential Functions: These grow or decay rapidly, and their graphs show either rapid increases or decreases.
Graphing Functions and Interpreting Their Behavior
To graph a function, it is essential to first understand its key features, such as the slope, intercepts, and asymptotes. By analyzing these elements, you can sketch the graph accurately. Here are some important tips for graphing:
- Intercepts: Find the points where the graph crosses the x-axis (x-intercepts) and the y-axis (y-intercepts).
- Slope: For linear functions, calculate the slope to understand the direction and steepness of the line.
- Asymptotes: Identify any vertical or horizontal asymptotes where the graph approaches but never touches a line.
By recognizing the unique characteristics of each function and graphing them accordingly, you will improve your ability to solve problems involving functions and understand their practical applications.
Preparing for the Multiple-Choice Section
The multiple-choice section can be a critical part of any assessment, requiring both strategy and knowledge to navigate effectively. This section typically tests your understanding of key concepts and your ability to apply them in various contexts. To approach these questions confidently, it’s important to be familiar with the material, recognize question patterns, and know how to eliminate incorrect answers efficiently.
In this section, we will discuss practical strategies for preparing for and tackling multiple-choice questions. By focusing on your understanding of fundamental principles and using thoughtful techniques, you can improve your accuracy and speed when answering these types of questions.
Understanding Common Question Formats
Multiple-choice questions often follow predictable formats. Recognizing these patterns can help you identify the correct answers more easily. Some common formats include:
- Direct Concept Questions: These questions test your knowledge of specific principles or formulas. They may ask you to identify the correct value, solve for a variable, or apply a rule to a given situation.
- Application Questions: These require you to apply knowledge to a new context, often involving word problems or scenarios that test your problem-solving skills.
- Comparative Questions: These may ask you to compare different expressions, equations, or graphs to identify which one meets the given criteria.
Techniques for Effective Answering
When faced with a multiple-choice question, there are several strategies you can use to increase your chances of selecting the right answer:
- Eliminate Clearly Wrong Answers: Start by removing choices that are obviously incorrect. This increases your chances of guessing correctly if you’re unsure.
- Look for Keywords: Pay attention to specific terms or phrases in the question that hint at the correct approach or formula.
- Check for Traps: Be aware of answers that may seem correct at first glance but contain subtle errors or misleading information.
- Time Management: Don’t spend too much time on any one question. If you’re stuck, make an educated guess and move on, returning to more difficult questions later.
By following these strategies and ensuring you are well-prepared, you can approach the multiple-choice section with confidence and efficiency.
Time Management Tips for the Final Assessment
Efficient time management is crucial when preparing for any large-scale assessment. The ability to allocate your time wisely during the assessment can make a significant difference in the outcome. By approaching the test with a clear strategy, you can ensure that you cover all the necessary material without feeling rushed or overwhelmed. In this section, we’ll discuss effective techniques for managing your time during the assessment.
Pre-Test Preparation

Before the assessment begins, setting up a time-management plan is essential. Knowing how much time to allocate to each section will help you stay on track. A few steps to take prior to the assessment include:
- Familiarize Yourself with the Structure: Understand the number of sections, the types of questions, and the time allotted for each part. This will help you mentally prepare for what to expect.
- Practice with Timed Tests: Take practice tests under timed conditions. This will help you gauge how long you need for each section and how to pace yourself.
- Prepare a Strategy for Each Section: Decide how long you’ll spend on each question type. For example, allocate more time to challenging problems and less time to easier ones.
During the Test
Once you begin the assessment, staying focused and managing your time properly becomes essential. Here are some tips to help you manage your time effectively during the test:
- Start with the Easy Questions: Begin by answering the questions that you feel most confident about. This will boost your confidence and ensure that you’re not wasting time on questions that you can answer quickly.
- Use the Process of Elimination: For difficult questions, eliminate obviously incorrect answers. This will help you make an educated guess more efficiently.
- Don’t Get Stuck on One Question: If you’re stuck on a question, move on and come back to it later if time permits. You don’t want to spend too much time on any one question.
- Keep an Eye on the Clock: Regularly check the time to ensure you’re on track. Adjust your pace as needed to ensure you have enough time for all sections.
Post-Test Review

After completing the assessment, review your answers if you have time. Even if you feel confident, it’s worth double-checking your responses to ensure accuracy. Focus particularly on questions you were unsure of, and make sure you haven’t missed any details.
The table below summarizes these key time management tips:
| Tip | Description |
|---|---|
| Familiarize Yourself with the Structure | Know the format and timing for each section before you start. |
| Practice with Timed Tests | Simulate real test conditions to get a feel for the timing. |
| Start with Easy Questions | Boost confidence and save time by tackling easier questions first. |
| Don’t Get Stuck on One Question | Move on if a question is taking too long; come back later if needed. |
| Double-Check Your Answers | If time permits, review your answers before submitting. |
By following these time management tips, you’ll be better prepared to tackle the assessment efficiently and effectively, ensuring that you can complete all sections on time and with confidence.